Fig. 3. Identification of C28 as a potent inhibitor against LMTK3.

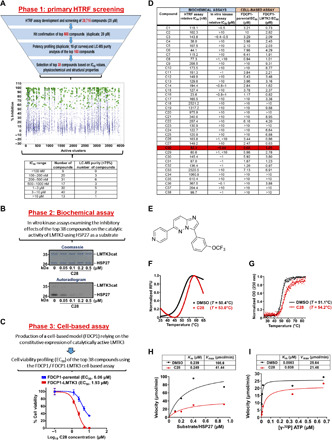
(A) Top: Experimental pipeline to identify LMTK3 inhibitors. Middle: HTRF data showing coverage of different inhibitors per active cluster. Green stars are the 868 compounds chosen for further confirmation, showing >50% mean inhibition (blue crosses are nonselected compounds). Selections were biased toward higher potency, sensible calculated physicochemical properties, and structural coverage within each cluster. Bottom: HTRF data showing the range of IC₅₀ values and purity of the top 160 compounds. (B) The IC₅₀ value for C28 against LMTK3cat was determined by in vitro kinase assays. (C) EC₅₀ values for C28 in FDCP1 and FDCP1-LMTK3 cell lines. Error bars represent the means ± SD from three independent experiments. (D) Table summarizing the IC₅₀ and EC₅₀ values of the top 38 compounds. (E) Chemical structure of C28. (F) Characteristic thermal denaturation curves of LMTK3 (black) and LMTK3/C28 complex (red) as monitored by DSF and (G) CD spectroscopy, indicating the increased protein thermodynamic stability upon ligand binding. T_m values from DSF were determined from the maximum in the first derivative of the fluorescence with respect to the temperature, or the midpoint in the transition region by fitting a Boltzmann sigmoidal to the CD data. Experiments were performed in triplicate. DMSO, dimethyl sulfoxide; OD, optical density; RFU, relative fluorescence units. (H) Kinetic analysis of HSP27 phosphorylation by LMTK3 in the absence or presence of C28. Kinetic parameters were determined from nonlinear regression fit of the initial reaction rates as a function of HSP27 concentration to the Michaelis-Menten equation using Prism 8. (I) Kinetic analysis as a function of ATP concentration for 0.6 μM HSP27 substrate, in the absence or presence of C28. Kinetic parameters were determined from nonlinear regression fit of the initial reaction rates as a function of ATP concentration to the Michaelis-Menten equation using Prism 8.