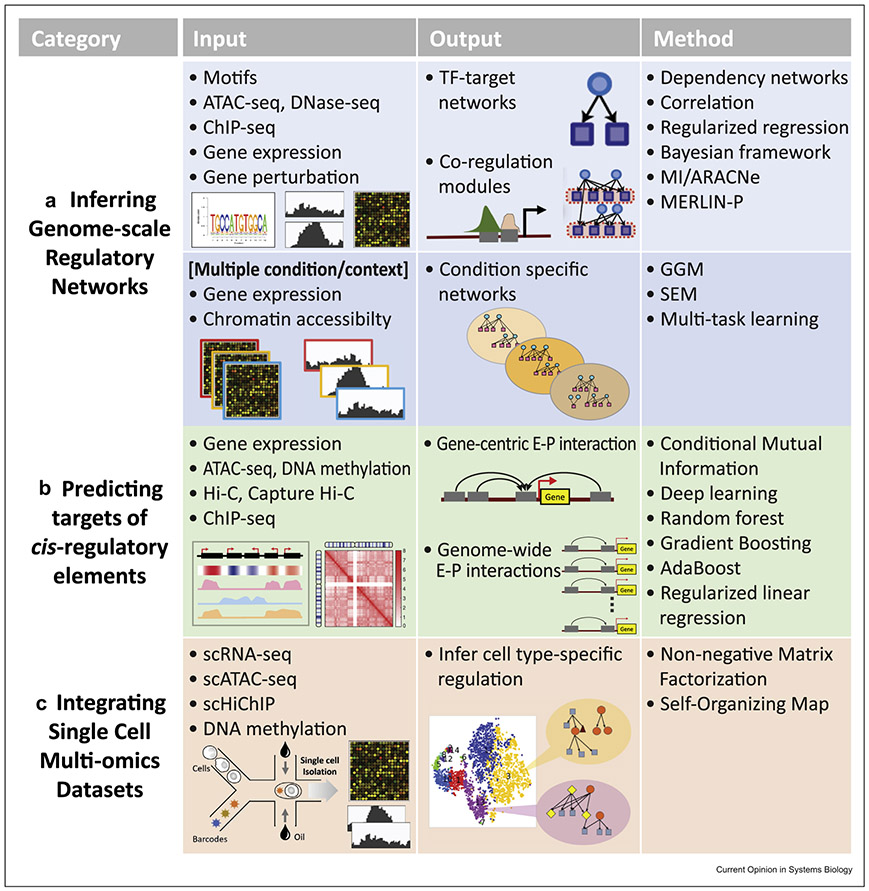
Figure 2. Classes of problems in gene regulation that integrate diverse data types and computational approaches to address these problems.

For each class of problems, the input data, outputs, and the algorithmic components used are shown. (a) Inference of genome-scale regulatory networks in a specific condition or across multiple conditions. These methods learn the structure of the network by predicting relationships between TFs and target genes and integrate gene expression with static data from public databases and context-specific data from ChIP-seq and ATAC-seq experiments. Methods use a variety of approaches to infer networks, including Gaussian graphical models (GGMs), dependency networks, mutual information (MI). Context-specific networks are learned by joint inference of networks across multiple conditions. Multi-task learning is a popular framework to enable information sharing across different contexts. (b) Predicting target genes of regulatory sequence elements. These methods use regulatory genomic data sets such as ChIP-seq, ATAC-seq, and 3D genome organization assays to identify targets of cis-regulatory elements. Regression and classification approaches have been developed to either predict counts or discriminate between an interacting and noninteracting pair. (c) Integration of different types of single-cell omic measurements to identify cell type–specific gene regulatory networks. These methods leverage single-cell RNA-seq (scRNA-seq) and scATAC-seq and occasionally bulk data sets. Methods typically use clustering and dimensionality reduction, for example, via matrix factorization, to define data set–specific clusters followed by linking the clusters. Some methods focus on genic regions, while others can incorporate auxiliary data sets such as HiChIP to link to genes. GGM: Gaussian graphical model; SEM: structural equation model; TF: transcription factor.