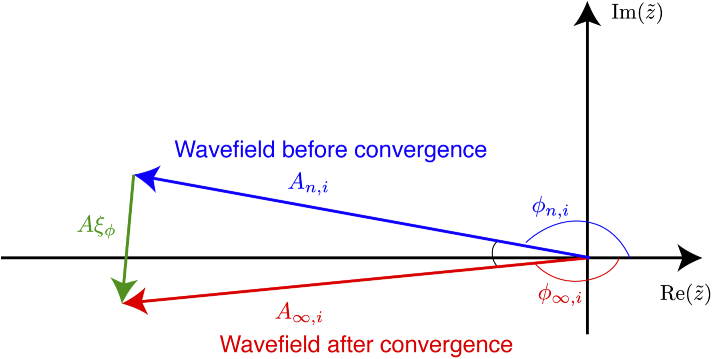
Fig. 3.

Illustration of the metric for measuring the RMS average $\overline{A}{\xi }_{\varphi }$ of the magnitude error at one pixel $i$ between the complex value before convergence ($A_{n,i}\exp [i{\varphi }_{n,i}]$; shown in blue) and after convergence ($A_{\mathrm{\infty },i}\exp [i{\varphi }_{\mathrm{\infty },i}]$; shown in red). When obtaining a particular measure of the phase difference ${\varphi }_{n,i}-{\varphi }_{\mathrm{\infty },i}$ from a complex value $\tilde{z}=A\exp [i\varphi ]$ on the real (Re) and imaginary (Im) plane, one could obtain erroneous values in the case shown where the phase before convergence is reported as $\pi -{ϵ}_{n,i}$ while the phase after convergence is reported as $-(\pi -{ϵ}_{\mathrm{\infty },i})$, one would obtain an erroneous phase difference ${\varphi }_{n,i}-{\varphi }_{\mathrm{\infty },i}$ of near $2\pi$. Calculating the RMS difference between complex wavefields (Eq. (24)) circumvents this problem by measuring the end-to-end distance between the red and blue vectors at individual pixels $i$, a result that does not require phase wrapping. When the moduli $A_{n,i}$ and $A_{\mathrm{\infty },i}$ are similar, the average modulus of the green vector (labeled here as $\overline{A}{\xi }_{\varphi }$ using Eq. (24)) is approximately linearly related to the RMS average of $\overline{A}|{\varphi }_{n,i}-{\varphi }_{\mathrm{\infty },i}|$ subtended by the blue and red vectors.