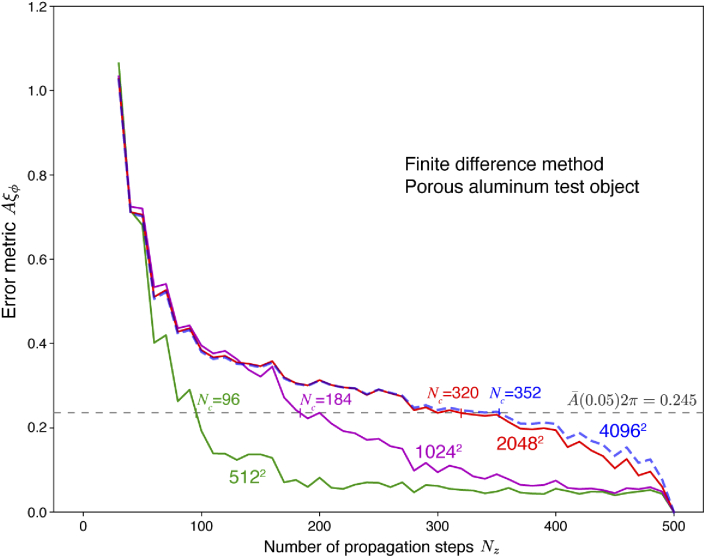
Fig. 8.

Convergence of the finite difference approach as a function of transverse array size for the porous aluminum object. As in Fig. 7, the indicated size of transverse array (ranging from ${512}^2$ to ${4096}^2$ pixels) was extracted from the object, and the total object thickness $t=147.5$ $\mathrm{\mu }$m was bilinearly sampled along the propagation direction $\hat{z}$ to vary $N_z$. For each array size, the minimum number of slices $n_C$ (Eq. (26)) was calculated using the convergence threshold ${[\overline{A}{\xi }_{\varphi }]}_{\text{Al}}=0.245$ of Eq. (30). As can be seen, the finite difference method converges more quickly with smaller transverse arrays, reaching $n_C=96$ (with slice thickness ${\mathrm{\Delta }}_z=1.54$ $\mathrm{\mu }$m) at ${512}^2$ transverse grid size with this irregular object.