Fig. 10.

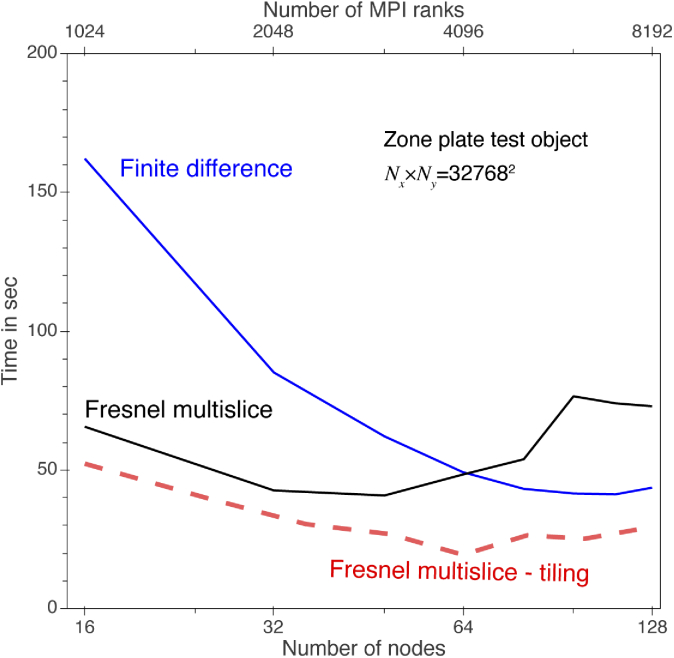
Time for calculating the exit wave from the zone plate test object as a function of the number of nodes used. This “strong scaling” test was done with a constant transverse grid size of $N_x\times N_y={32768}^2$ pixels on the computational cluster “theta” (see Table 1), and using the number of slices $n_C$ each algorithm required for convergence to the error tolerance ${[\overline{A}{\xi }_{\varphi }]}_{\text{zp}}$ of Eq. (28) (the resulting values of $n_C$ were consistently within 1 or 2 slices of the values shown in Fig. 9). While the finite difference method takes the longest amount of time with a small number of nodes, it benefits the most from increased parallelization so that the calculation time drops significantly by the time 128 nodes are employed. The full-array Fresnel multislice method shows only a modest time decrease as more nodes are employed, until at 64 nodes the calculation time begins to increase due to the requirement for considerable data communication between nodes. Because the tiling-based short-distance Fresnel multislice approach allows each node to proceed through to the exit wave plane before inter-node communication is again required, it takes the least time but after 64 nodes one again sees a slight increase in calculation time if additional nodes are used. Note that 64 nodes corresponds to a transverse array size of 4096² pixels per node. Further details on this “strong scaling” test are provided in Fig. 11.