Fig. 11.

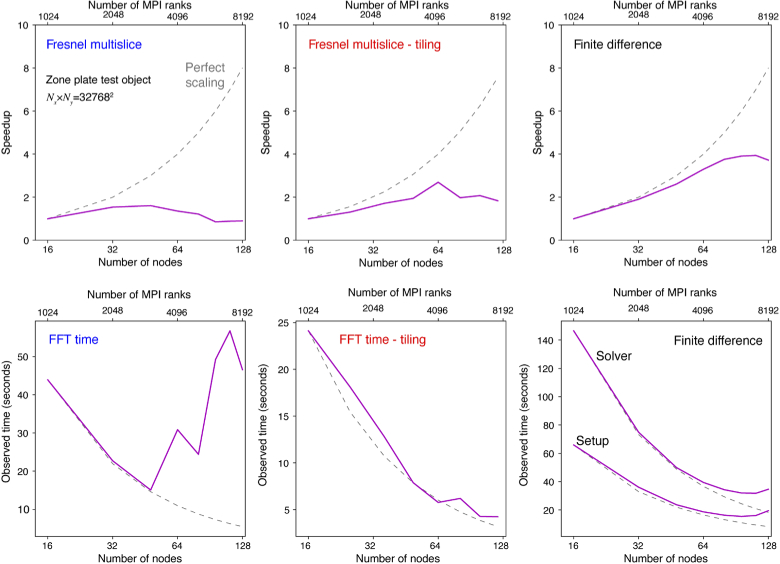
Further details on the “strong scaling” test results shown in Fig. 10. These tests were of the zone plate test object on a $N_x\times N_y={32768}^2$ pixel transverse grid. For each of the three calculation methods, we show at top the speedup versus the number of nodes used (with a a linear “perfect scaling” trend showing up as a curved line on this log-linear plot). This shows that the finite difference method has the best scaling to calculation speedup with increased number of nodes. At bottom we show the time required for key operations in the various methods: the time required for a fast Fourier transform (FFT) in the full-array Fresnel multislice and tiling-based short-distance Fresnel multislice methods, and the time for problem setup and then problem solution for the finite difference method. With the full-array FFT approach, the advantage of having more processors is outweighed by data communication overhead when 64 or more nodes are used.