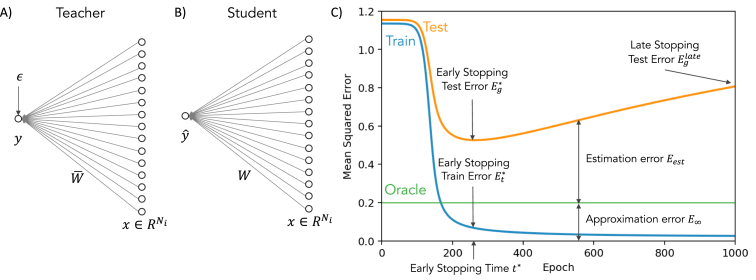
Fig. 1.

Learning from a noisy linear teacher. (A) A dataset $\mathcal{D}=\{x^{\mu },y^{\mu }\},\mu =1,\dots ,P$ of $P$ examples is created by providing random inputs $x$ to a teacher network with a weight vector $\overline{w}$, and corrupting the teacher outputs with noise of variance ${\sigma }_{ϵ}^2$. (B) A student network is then trained on this dataset $\mathcal{D}$. (C) Example dynamics of the student network during full batch gradient descent training. Training error (blue) decreases monotonically. Test error, also referred to as generalization error, (yellow), here computable exactly (4), decreases to a minimum $E_g^{\ast }$ at the optimal early stopping time $t^{\ast }$ before increasing at longer times ($E_g^{\text{late}}$), a phenomenon known as overtraining. Because of noise in the teacher’s output, the best possible student network attains finite generalization error (“oracle”, green) even with infinite training data. This error is the approximation error $E_{\infty }$. The difference between test error and this best-possible error is the estimation error $E_{\text{est}}$. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)