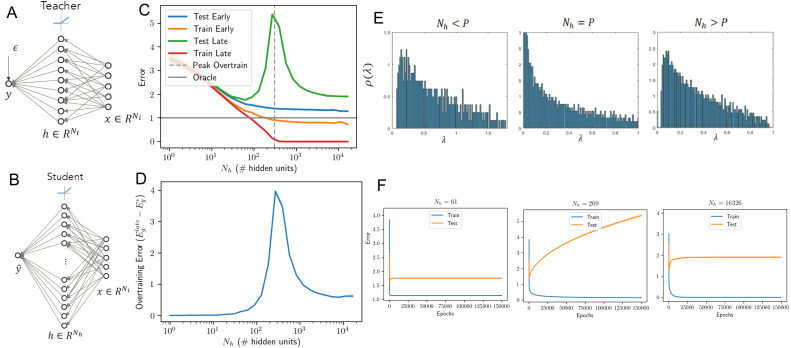
Fig. 7.

Learning from a nonlinear teacher. (A) The teacher network ($N_t$ ReLUs). (B) The student network ($N_h$ ReLUs, but only the output weights are trained). (C) Effect of model complexity. Optimal early stopping errors as a function of number of hidden units $N_h$ for the case $\text{SNR}=1,\text{INR}=0,N_i=15,N_t=30$ and $P=300$ training samples. Shaded regions show $\pm 1$ standard error of the mean over 50 random seeds. (D) Overtraining peaks at an intermediate level of complexity near the number of training samples: when the number of free parameters in the student network equals the number of samples (300). (E) The eigenspectrum of the hidden layer of a random non-linear neural network with $P=1000$ samples and an $N_i=100$ dimensional input space. We consider three cases and find a similar eigenvalue density to a rescaled Marchenko–Pastur distribution when we concentrate only on the small eigenvalues and ignore a secondary cluster of $N_i$ eigenvalues farther from the origin. Left: Fewer hidden nodes than samples ($N_h=500$ hidden units) leads to a gap near the origin and no zero eigenvalues. Center: An equal number of hidden nodes and samples ($N_h=1000$) leads to no gap near the origin so that eigenvalues become more probable as we approach the origin. Right: More hidden nodes than samples ($N_h=2000$) leads to a delta function spike of probability 0.5 at the origin with a gap to the next eigenvalue. (F) Average training dynamics for several models illustrating overtraining at intermediate levels of complexity. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)