Repetitive optical coherence elastography measurements with blinking nanobombs

Abstract

Excitation of dye-loaded perfluorocarbon nanoparticles (nanobombs) can generate highly localized axially propagating longitudinal shear waves (LSW) that can be used to quantify tissue mechanical properties without transversal scanning of the imaging beam. In this study, we used repetitive excitations of dodecafluoropentane (C5) and tetradecafluorohexane (C6) nanobombs by a nanosecond-pulsed laser to produce multiple LSWs from a single spot in a phantom. A 1.5 MHz Fourier-domain mode-locked laser in combination with a phase correction algorithm was used to perform elastography. Multiple nanobomb activations were also monitored by detecting photoacoustic signals. Our results demonstrate that C6 nanobombs can be used for repetitive generation of LSW from a single spot for the purpose of material elasticity assessment. This study opens new avenues for continuous quantification of tissue mechanical properties using single delivery of the nanoparticles.

1. Introduction

It has been well documented that cancer and other pathological changes can significantly transform local tissue biomechanical characteristics [1–4]. Therefore, various elasticity imaging modalities have been developed where an external force is applied to a sample, and the subsequent mechanical response is measured [5–8]. Optical coherence elastography (OCE) is an interferometric-based, non-invasive imaging modality and one of such elastography techniques, which can provide micrometer-scale spatial resolution [9,10]. Further, using phase of the OCE signal, the sensitivity of the method to the measured displacement can be boosted to a nanometer level [11,12].

Several methods have been employed for the assessment of elastic properties using OCE. Dynamic or transient OCE often involves inducing and characterizing mechanical waves in a sample and then quantifying mechanical parameters such as viscoelasticity through appropriate models. Different mechanical waves can be induced within tissue, such as shear waves, Rayleigh waves, and longitudinal waves [13,14]. Transversely propagating shear waves can provide information about transverse elasticity differences and longitudinal shear waves (LSWs) can provide the elasticity gradients along the depth [15–19]. Coupling detection of a transverse shear wave and of an LSW provides opportunities for measurements of elastic properties in anisotropic tissues in both axial and lateral directions simultaneously [17]. As the displacement of LSW is polarized along the propagation direction, it can be measured by phase-sensitive OCE [16,17,20].

Contact-based mechanical excitation has traditionally been used to induce LSWs [17,19]. However, laser-induced excitation of elastic waves provides a noncontact all-optical approach for OCE [21] with an advantage of measuring highly localized tissue biomechanical properties due to the high frequency of the induced elastic waves [22].

During optical excitation, the energy is converted to elastic waves following absorption of the excitation light and localized thermal expansion of the tissue. Application of an ink layer to a sample was previously used to enhance local absorption of the pulsed laser energy [21]. Alternatively, it was shown that dye-loaded perfluorocarbon (PFC) nanodroplets can undergo a liquid to gas transition upon excitation with a pulsed laser. This phenomenon has been extensively used for both imaging and therapeutic applications [23–27]. In photoacoustic (PA) imaging the light-induced phase change in PFC nanodroplets results in a very strong PA signal due to droplet vaporization rather than a photothermal tissue expansion [24]. Recently, we explored the laser-triggered phase-changing PFC nanodroplets for induction of highly localized, high-frequency elastic waves for evaluation of tissue biomechanical properties [20,22].

Specifically, we showed that dodecafluoropentane (C₅F₁₂, boiling point at 29 °C) nanodroplets loaded with either Cy3 or Epolight 3072 dyes (C5 nanobombs) can be used to produce high-frequency localized LSWs which can be imaged using OCE. Because of the fast expansion of the phase-changing PFC nanodroplets that produces localized loading we call them “nanobombs”. However, these studies did not explore the feasibility of repeated OCE measurements from a single spot in a sample; such measurements would be important in longitudinal evaluation of changes in tissue mechanical properties. Previously, extended PA imaging over multiple laser pulse excitations was achieved with higher boiling point PFC nanodroplets (i.e., tetradecafluorohexane (C6) with boiling temperature of 56°C) that can undergo repeated cycles of laser-triggered vaporization followed by spontaneous recondensation [28,29]. It was shown that the vaporization of C6 nanodroplets can result in formation of transient gaseous microbubbles followed by re-condensation back into stable nanodroplets within milliseconds. This repeatable laser-triggered vaporization/re-condensation processes (a.k.a., “blinking”) allows multiple inductions of liquid-to-gas phase changes in the nanodroplets, thus enabling low-background PA and ultrasound imaging.

Here we explored this concept in generation of repetitive LSWs for OCE (Fig. 1). We demonstrated that: (1) perfluoropentane (C5) based nanobombs that were introduced in our previous work cannot be used for repetitive generation of LSWs; this is a significant limitation in studies of biological processes where potential changes need to be accessed over time; and (2) most importantly, we addressed this limitation by introducing and evaluating C6 nanobombs that can recondense following laser excitation thus allowing repeated excitation and multiple generations of LSWs. Furthermore, the generated LSWs can be used for consistent determination of Young’s modulus in tissue mimicking phantoms. This property can be used for longitudinal elasticity measurements in biological specimen following a single delivery of the C6 nanobombs.

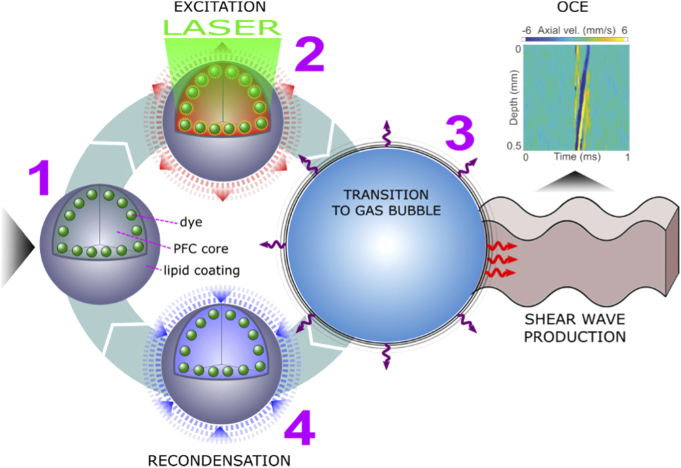
Fig. 1.

Illustration of a PFC nanobomb’s blinking behavior for generation of repetitive LSWs. (1) A C6 nanobomb consists of the tetradecafluorohexane core coated with a lipid shell with embedded NIR-absorbing dye molecules. (2) A pulsed NIR laser excitation is absorbed by the dye molecules that heat the core leading to (3) a transient liquid-to-gas transition and expansion. The expansion generates a shear-wave that is detected by OCE. (4) The microbubble spontaneously recondenses within few milliseconds back to the initial droplet (1) and the cycle can be repeated again.

2. Materials and methods

2.1. Preparation and characterization of nanoparticles

The nanodroplets were prepared as described earlier [20,22,23] with some modifications. Specifically, 1 mg of the Epolight 3072 dye (absorption peak 1054 nm, band width ∼250 nm, Epolin Inc.) [25,28], 18 mg of 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC), 1.7 mg of 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-methoxy-polyethyleneglycol-2000 (DSPE-PEG-2000), and 0.3 mg of cholesterol (Avanti Polar Lipids, Inc.) were dissolved in 2 mL of chloroform. Epolight 3072 dye has the absorption maximum at 1054 nm and it was used to enable excitation using a NIR laser. The solution of lipids and the dye was vacuum dried in a rotary evaporator (Cole-Palmer Instrument Company) at 40 °C for ∼20 min until formation of a thin lipid cake. Subsequently, the lipid cake was hydrated by addition of 2 mL of deionized water on a shaker at 250 rounds/min for 30 min. In parallel, 150 µL of either dodecafluoropentane (for synthesis of C5 nanobombs, FluoroMed) or tetradecafluorohexane (for synthesis of C6 nanobombs, Sigma-Aldrich) were mixed with 150 µL of ice-cold deionized water and 100 µL of 1% (v/v) aqueous solution of 1H,1H,2H-Perfluoro-1-hexene,3,3,4,4,5,5,6,6,6-nonafluoro-1-hexene (Sigma-Aldrich) to produce a core mix. The core mix was vortexed for 20 s, followed by sonication in a benchtop ultrasonic bath (CPX-962-218R, Fisher Scientific) in ice-cold water for additional 30 s. Then, the rehydrated lipid cake was added to the core mix, followed by vortexing for 30 s and sonication in the benchtop ultrasonic bath in ice-cold water for another 1 min. After that, the mixture was sonicated using the CPX 500 ultrasound probe with a 2 mm tip (Cole Palmer) for two 1 min cycles at 25% maximum amplitude, separated by 20 s of vortexing. The suspension was left on ice for 5 min and then it was washed twice with deionized water at 3100 G for 15 min. The final pellet was re-suspended in 1 mL of deionized water. Blank nanobombs (no dye) were prepared using the same protocol except no dye was added to the mix during lipid cake preparation. Size of nanobombs was measured by dynamic light scattering (DLS) using intensity (Delsa Nano C, Beckman Coulter, Inc.). The amount of perfluorocarbon in nanobomb preparations was measured using ¹⁹F NMR. NMR measurements were performed in 5 mm NMR sample tubes (Wilmad-LabGlass) containing a mixture of 10 µL of a nanobomb sample, 75 µL of 0.5% solution of trifluoroacetic acid in deuterium oxide (both from Sigma-Aldrich), and 400 µL of deionized water. A typical NMR scan was performed on 500 MHz NMR spectrometer (Bruker Corporation) with the following parameters: 0.58 s acquisition time, 16 signal averages (with phase cycling), and 5 s relaxation delay. ¹⁹F concentration was determined by integrating NMR peaks of either dodecafluoropentane or tetradecafluorohexane and by normalizing them by the integrated peaks of the trifluoroacetic acid.

2.2. Phantom preparation

All polyacrylamide (PAA) phantoms had the same two-layered design with a bottom layer serving as a support (identical in all phantoms, no nanodroplets added) and top layers varying in PAA concentration and nanodroplet content between samples as outlined below.

The proportion (v/v) of reagents in PAA polymerization mixtures was as following: (1) 25% or 27.5% of 40% aqueous acrylamide solution (Ambion Inc.) to prepare 10% and 11% PAA phantoms, respectively, (2) 3.5% of Intralipid (Sigma-Aldrich), (3) 1% of 438 mM solution of ammonium persulfate (Sigma-Aldrich), (4) 0.2% of tetramethyl ethylenediamine (Sigma-Aldrich), and (5) 70.3% and 67.8% of deionized water in 10% and 11% PAA phantoms, respectively. For each phantom, 8 mL of 10% PAA mixture was poured in a single well of a 6-well plastic plate. The mixture was allowed to polymerize for 30 minutes forming the bottom support layer of approximately 10 mm thickness. The excess liquid was removed by pipetting and another 1.5 mL aliquot of the PAA mixture with varying PAA concentrations and nanodroplet content (see Table 1) was poured over the bottom layer to form the top layer of ∼1 mm thickness that was confirmed by OCT (Fig. 2(f)). After final polymerization, the two-layered PAA gels were stored in a closed plastic 6-well plate to prevent them from drying.

Table 1. Overview of PAA concentrations, nanodroplet type, size, and content in the top layer of each phantom used in this study (Nb = nanobomb).

Sample #	Description	PAA concentration	Nb core	Dye	Nb size
1	Nb with dye	10%	C6	Epolight 3072	344 ± 4 nm
2	Nb with dye	11%	C6	Epolight 3072	344 ± 4 nm
3	Nb with dye	11%	C5	Epolight 3072	292 ± 4 nm
4	Nb without dye	11%	C6	no dye	270 ± 8 nm
5	Nb without dye	10%	C6	no dye	270 ± 8 nm
6	control (no nb)	10%	no nb	no dye	-

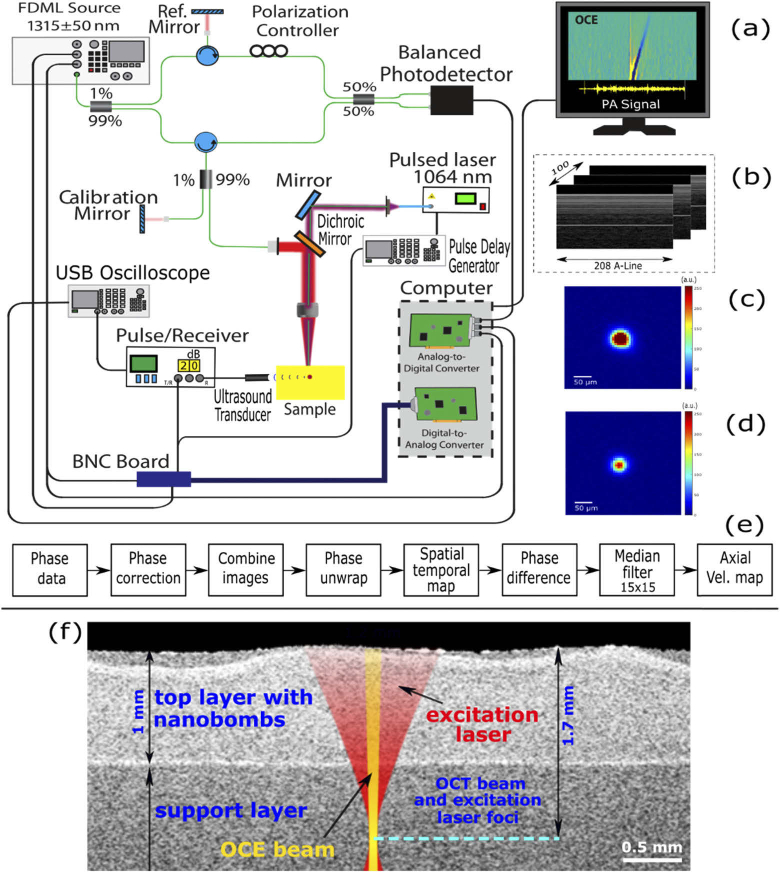
Fig. 2.

(a) Schematic of the OCE system and photoacoustic signal detection setup. (b) Continuous M-mode frames grouped in 100 sequential frames with 208 A-lines per frame; (c) and (d) beam profiles (8-bit image) of pump and FDML swept source lasers, respectively. (e) Post-processing flow chart. (f) Positions of the OCE and the excitation laser beams relative to phantom’s layered structure obtained by OCT.

Phantoms containing either C5 or C6 nanodroplets in the top layer were prepared by adding a suspension of nanodroplets to the water fraction of respective PAA mixtures. The concentration of nanodroplets in the top layer was kept the same for all phantoms at 113 mM of ¹⁹F content. The average size of nanodroplets, measured by DLS, was ∼270-345 nm. Compositions of top layers of PAA phantoms used in these studies are summarized in Tab. 1.

2.3. Experimental setup, data processing and statistical analysis

The setup for OCE with nanobombs (nbOCE) has been previously described [20,30]. Figure 2 shows the ultra-fast OCT system equipped with a 4× buffered FDML swept source laser. The swept source system has the A-scan rate of 1.5 MHz, scan wavelength of (1315 ± 50) nm, maximal output power of 160 mW, axial resolution of 16 µm, and sensitivity of 104 dB.

The swept source (probe) laser was co-aligned with a 6 ns-pulsed pump laser (Polaris II, New Wave Research Inc.) emitting 1064 nm NIR light. The pump laser was matched with the absorption band of the Epolight dye in the nanobombs. A beam camera (LaserCam-HR II 2/3”, Coherent Inc.) was used to image beam profiles shown in Fig. 2. The axial position of the camera was verified by OCT. Thus, the beam diameters were measured as a function of the axial position. The focus 1/e² diameters were 68 µm and 58.6 µm for pump and probe lasers, respectively. For both lasers, beam profiles in focus are shown in Fig. 2(c) and (d). The pump laser focus was shifted into tissue phantoms resulting in the surface beam diameter of ∼1.2 mm. The focus shift would correspond to ∼1.7 mm depth in a non-diffusive scattering medium. In this study, the pump laser was operating at pulse energies E_p of either 630 ± 30 µJ or 1010 ± 50 µJ that were chosen based on our previous study [20]. The corresponding surface fluence was estimated using a Gaussian pulse with waist radius w given by the following equation Φ=2E_p/(πw²). Thus, the estimated surface fluence was 99 mJ/cm² or 159 mJ/cm².

The pump laser was operating in the single shot mode and was synchronized with the M-mode trigger. By this synchronization, a sample was continuously probed over a period of 13.3 ms after each pump laser pulse. As illustrated in Fig. 2(b), 100 M-mode frames were acquired with 208 A-lines each. The sample surface and the calibration mirror were offset by 0.5 mm and 2 mm, respectively, relative to the reference mirror. Simultaneously with the recording of A-lines, a photoacoustic signal was measured with a 3.5 MHz transducer, then amplified with a pulse receiver and saved on a computer using an USB oscilloscope.

Data processing was previously described in [20] and is summarized in the data processing flow chart shown in Fig. 2(e). Briefly, the intensity data was used to determine the approximate position of the calibration mirror. The key element was the phase correction because it significantly improved phase stability as demonstrated before. This phase correction reduced a phase noise and phase jittering between buffers and turned a noisy LSW trace into a clear signal. For the phase correction, the best calibration depth was determined by shifting the approximate mirror position to find the depth with the best phase stability or, in other words, the depth with minimum standard deviation of the velocity within each M-mode. The phase was calibrated for each M-mode by subtracting a scaled phase. The calibrated phase ${\phi }_{\text{cal}}$ is a function of the depth z and mirror position z_m.

$${\phi }_{\text{cal}}(z)={\phi }_0(z)-{\phi }_0(z_{\mathrm{m}})\frac{z}{z_{\mathrm{m}}}$$ (1)

The M-mode frames were combined by calibrating all A-lines of each M-mode frame with the last A-line values of the previous M-mode frame, for each depth of the A-line. The phase was unwrapped and the displacement was calculated. For each depth, the mean of background displacement was subtracted from the displacement. The background was defined as the displacement before excitation. The background corrected displacement was differentiated and the resulting axial velocity map was filtered to enhance the visibility of LSWs.

Two-way ANOVA (comparison between multiple groups) and unpaired t test (comparison between two groups) were used for statistical analysis of Young’s moduli measurements, also specified in figure descriptions and text whenever applicable.

3. Results

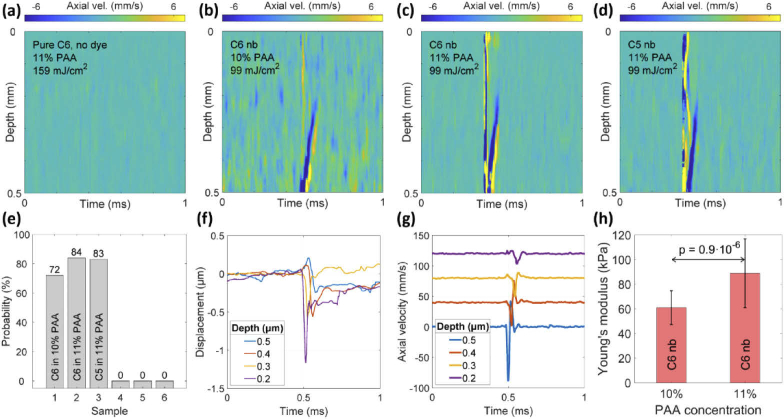
OCE measurements of control samples, which contained PFC nanodroplets without dye (samples 4-6, Table 1), showed no generation of LSWs as expected (Fig. 3(a)) even at fluences higher than 159 mJ/cm². Figure 3(b) and (c) show the spatiotemporal maps of C6 nanobomb phantoms with 10 and 11% PAA, respectively; the maps represent propagation of elastic waves in the phantoms following a laser excitation pulse. The vertical strip at 0.5 ms is the displacement generated by a fast-propagating P-wave. The P-wave is followed by a slower longitudinal shear wave (S-wave) visible as a tilted strip propagating upwards. The downward propagation was not detected due to the deterioration of phase stability with depth. Figure 3(d) illustrates elastic waves in sample 3 with C5 nanobombs. In general, no apparent qualitative differences were observed between longitudinal shear waves generated by C5 and C6 nanobombs. The central frequency of the shear wave axial velocity was in the range of 10-40 kHz and it rapidly decreased with distance because of a strong attenuation of the high-frequency components of the signal.

Fig. 3.

Spatiotemporal axial velocity maps of (a) sample 4 with C6 nanodroplets, (b) sample 1 with C6 nanobombs in 10% PAA, (c) sample 2 with C6 nanobombs in 11% PAA, and (d) sample 3 with C5 nanobombs in 11% PAA. (e) Probability of generating longitudinal shear waves in samples 1 through 6. (f) Displacement (phase) and (g) axial velocity profile corresponding to the map (b). (h) Estimation of Young’s moduli for C6 nanobomb phantoms with 10% and 11% PAA concentrations (61 ± 14 kPa and 89 ± 30 kPa). Statistical comparison was done using unpaired t test, n = 36 per PAA concentration.

The probability of generating a longitudinal shear wave in response to a single laser pulse varied from 72% to 84% in samples 1 to 3. In control samples 4 to 6, the generation probability was zero due to the lack of the absorbing dye. The probability was determined by evaluating the occurrence of LSW at no less than 100 different positions for each sample. A positive or “1” event was associated with a clear LSW generation and an absence of a clear LSW after a single laser pulse was counted as a negative or “0” event. The generated LSWs were randomly distributed over phantom’s surface. Figure 3(f) and (g) show representative displacement and axial velocity profiles corresponding to measurements at 4 different depths. The longitudinal shear wave velocity c_g was calculated by fitting the time points of the minima in axial velocity profiles (Fig. 3(g)) as a function of the corresponding depths. The group velocity of an LSW can be accurately calculated using ∼ 0.2 mm travel distance along the depth. Our targeted length in this study was between 0.4 to 0.6 mm. If less than 0.2 mm distance is used then a deviation of the velocity estimate might be too high for a reliable measurement. Then, Young’s modulus was estimated using the shear wave equation [13,14]:

$$E=2\varrho (1+v)c_{\mathbf{\text{g}}}^2$$ (2)

with Poisson ratio of $v$ = 0.49 and material density of ϱ = 1000 kg/m³. As shown in Fig. 3(h), the resulting mean and standard deviations of Young’s moduli measured for C6 nanobombs in 10% and 11% PAA phantoms were 61 ± 14 kPa (n = 36) and 89 ± 30 kPa (n = 36), estimated using multiple measurements over different regions of samples 1 and 2, respectively. The t-test between two groups resulted in a p value of 0.9 × 10⁻⁶ indicating statistically significant difference in Young’s moduli measured at different PAA concentrations. Young’s modulus of sample 3 with C5 nanobombs measured over different regions of the phantom was 90 ± 11 kPa (n = 6). Previously, we demonstrated that measurements of Young’s moduli using nbOCE with C5 nanobombs are in a good agreement with mechanical testing that showed Young’s moduli 55.7 ± 14.6 and 84.3 ± 11.2 for 10% and 11% PAA phantoms, respectively [20].

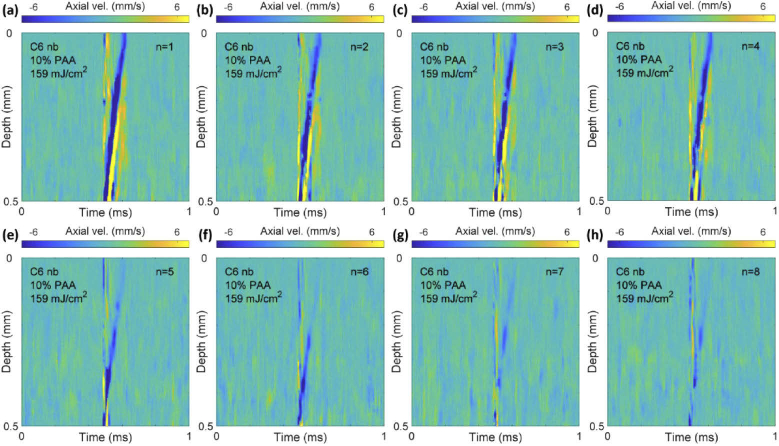
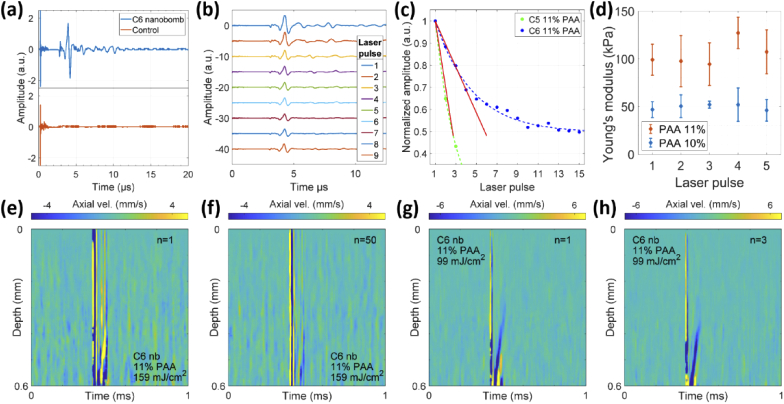
Having established that C6 nanobombs can be used to estimate Young’s modulus, we evaluated their performance in repetitive nbOCE measurements and compared it with C5 nanobombs. The same spot on sample 1 was repeatedly excited by the pump laser operating at approximately 1 Hz rate and constant pulse energy (Fig. 4). The detected spatiotemporal maps showed the same characteristics, but the displacement amplitude slowly decreased with the number of laser pulses (Fig. 4(a) to (h)). For all 8 maps, the LSW traveled at approximately 0.4 mm in 0.1 ms.

Fig. 4.

From (a) to (h): spatiotemporal axial velocity maps of 8 consecutive shots on the same spot on sample 1 at approximately 1 Hz repetition rate and 159 mJ/cm² fluence.

In parallel with OCE, the nanobomb explosions were also measured by an ultrasound transducer. Observations of LSWs always correlated with a PA signal in our experiments. Thus, co-registration of a PA signal was a useful tool in prediction of a successful OCE measurement. A typical PA signal generated in C6 nanobomb sample 1 is shown in Fig. 5(a); no PA signals were detected in control samples without nanobombs. The nanobomb excitation was clearly visible as the PA amplitude changed at 2.5 µs (Fig. 5(a)). Similar to the velocity maps (Fig. 4), the PA amplitude decreased after consecutive laser excitation pulses, but the signal shape did not change significantly as can be seen in Fig. 5(b).

Fig. 5.

(a) PA signal from control sample 4 and C6 nanobomb sample 2. (b) PA signals from the same spot on the C6 nanobomb sample 1 after consecutive laser excitation pulses. (c) Comparison of PA signal decay during repetitive laser excitations of C6 nanobombs and C5 nanobombs both in 11% PAA phantoms measured at 159 mJ/cm² laser fluence. (d) Comparison of Young’s modulus estimations as a function of consecutive laser excitations on the same spot on 10% and 11% PAA phantoms with C6 nanobombs (mean ± SD), n = 5-8 measurements per each PAA concentration/pulse number combination. Statistical analysis was done using ANOVA as described in the text. Spatiotemporal maps after the first (e) and the fiftieth (f) laser excitation pulses located on the same spot on sample 2 with C6 nanobombs. (g) and (h) The maps after the first (g) and the third (h) consecutive laser excitation pulses on C6 nanobomb sample 2 with reduced fluence of 99 mJ/cm².

The PA signal decayed significantly faster in sample 3 with C5 nanobombs compared to sample 2 with C6 nanobombs (Fig. 5(c)). The initial signal decrease was approximated by linear curves using the first three laser excitation pulses. The curves had slopes of -0.3 and -0.1 for phantoms with C5 and C6 nanobombs, respectively. A PA signal from C6 nanobombs was observed after more than 50 consecutive laser pulses at an excitation rate of 1 Hz. For C5 nanobombs, a PA signal was observed for only ∼10 consecutive pulses. This result correlated well with OCE measurements where the amplitude of LSWs in phantoms containing C5 nanobombs decreased faster and it was less repeatable after multiple laser excitations as compared to C6 phantoms.

For multiple excitations, Fig. 5(d) shows mean estimations and standard deviations of Young’s moduli obtained for the first 5 laser pulses in 10% and 11% PAA C6 nanobomb phantoms. We carried out 5-8 measurements for each phantom/pulse number combination. We performed simple effects two-way ANOVA, examining effects of PAA concentration and pulse number on measured Young’s moduli. Main effect analysis for pulse number in ANOVA showed that for both PAA phantom concentrations, the estimated Young’s modulus did not change significantly with a laser pulse number. Importantly, main effect analysis for PAA concentration in ANOVA showed that there was statistically significant difference (p < 0.001) between Young’s moduli measured for PAA 10% and 11%, respectively. The results of statistical analysis indicate that consecutive laser pulses do not alter the material stiffness as expected and multiple excitations of C6 nanobombs can be used to determine Young’s modulus repeatedly (Fig. 5(d)). LSWs were observed in C6 phantoms up to 50 consecutive laser excitation pulses (Fig. 5(e) and (f)). We also showed that multiple LSWs can be excited in C6 phantoms with a lower laser fluence of 99 mJ/cm². Furthermore, comparison of the spatiotemporal maps obtained at 159 mJ/cm² (Fig. 5(e) and (f)) and 99 mJ/cm² (Fig. 5(g) and (h)) shows that phase stability is more important for sensitive detection of LSW than the laser fluence as the displacements can be clearly seen under both excitation conditions after phase noise is suppressed.

4. Discussion

This work explored propagation of LSWs and assessment of Young’s modulus by optical excitation of blinking PFC nanodroplets (nanobombs) embedded in tissue-mimicking phantoms. We compared the ability of C5 and C6 nanobombs (i.e., PFC nanodroplets with perfluoropentane and perfluorohexane cores, respectively) to generate LSWs during consecutive laser excitations for repetitive OCE measurements. OCE was combined with photoacoustic measurements to study the generation of LSWs in more details. The addition of photoacoustics allowed real time monitoring of nanobomb excitation during the experiment.

LSWs are divergence- and curl-free type of waves generated at the near field of a source and can be detected in the far field [31]. Usually, LSWs, together with other types of elastic waves, are generated when a motion source is being displaced towards a main direction. Even though nanobombs are distributed within an extended layer in the elastic phantom, their motion activation (explosion) is constrained only to a focal region with sufficient fluence of the excitation pulsed laser which can be interpreted as a local source in the far field similar to our previous study, where propagation of transverse shear wave after nanobombs activation was investigated [22].

First, we established that OCE with C6 nanobombs resulted in the same Young’s moduli as estimated using C5 nanobomb, air-pulse or mechanical testing [20]. The probability to generate an LSW after the first laser pulse was equally high for both types of nanobombs. However, as expected the PA signal of phantoms containing C5 nanobombs showed a fast decrease after repeated laser excitations. Specifically, for C5 nanobombs, the PA signal after the third laser pulse was already lower than the PA signal generated by any consecutive pulses applied to C6 nanobomb phantoms in the study shown in Fig. 5(c). Consequently, Young’s modulus could not be determined for repeated laser excitations of C5 nanobombs due to the fast signal decay. This fast decay is most likely associated with a relatively low probability of recondensation of C5 nanobombs due to a low boiling temperature of ∼29°C of perfluoropentane (the liquid core material of C5 nanobombs) that was close to the ambient temperature in our experiments. The observed consecutive excitations of C5 nanobombs might be associated with their partial recondensation that diminishes with multiple laser pulses. Further, it is conceivable that only a fraction of nanobombs in the excitation volume was excited during each laser pulse thus allowing consequent PA signal generation in phantoms with C5 nanobombs. The residuals of nanobomb explosions such as impurities or dye particles could also have an impact on re-excitation. However, the dye alone has a low LSW generation probability of 10% as was shown previously [20] and the probability for empty nanobombs is zero.

In contrast, the PA signal amplitude decays much slower and reaches a plateau at ∼50% of the initial signal in C6 phantoms after multiple laser excitations (Fig. 5(c)). The initial decay is likely associated with irreversible vaporization of a fraction of C6 nanobombs that are bigger than average, as it was shown that the possibility of recondensation of C6 nanodroplets is inversely proportional to their size, even when the same vaporization energy is applied [29]. The continuous PA signal generation also known as “blinking” of dye-loaded perfluorohexane nanodroplets (i.e., C6 nanobombs) has been extensively studied and is shown to be associated with a repeated laser-triggered vaporization-recondensation cycle of the nanodroplets (Fig. 1) [28,29]. We demonstrated that consequent laser excitations of blinking C6 nanobombs can produce up to fifty LSWs in tissue-mimicking phantoms (Fig. 5(e) and (f)). The probability to generate consecutive LSWs from the same spot on the tissue phantom was above 90%. Furthermore, generated LSWs were used to estimate local Young’s modulus with high repeatability. Thus, the use of blinking C6 nanobombs enables a fast recording of statistical data on the sample’s stiffness, measuring small areas of interest and longitudinal OCE measurements. Note that if the motion signal is weak or noisy, the calculation of group speed is more subjected to noise, and therefore, the estimation of speed and Young’s modulus can be inaccurate. Figure 5(d) shows that the calculation was successful for at least the first five consecutive laser pulses.

It is important to note that the effective boiling temperature of perfluorocarbon nanodroplets is significantly increased compared to a bulk liquid form due to Laplace pressure which increases with a decrease in nanodroplet size [32–35]. Therefore, nanodroplets with perfluoropentane (C5) and perfluorohexane (C6) cores were shown to be stable at 37°C temperature even though the boiling temperature of perfluoropentane is 29°C [24,25,28,29,36]. Further, it was demonstrated that the recondensation probability of microbubbles formed after liquid-to-gas phase transition of C5 and C6 nanodroplets is much higher for C6 nanodroplets at 37°C temperature due to a relatively high boiling temperature of 56°C of perfluorohexane [29,36]. This effect was used for repeatable photoacoustic imaging of C6 nanodroplets under physiological conditions [27,28]. This data indicates that C6 nanobombs described in our studies can be used at physiological temperatures.

Another important consideration is a role of mechanical properties and boundaries of a medium on the probability of nanobomb recondensation. It was previously shown that a boundary in close vicinity to a bubble can affect bubble dynamics if a ratio between the distance from the origin of the bubble and the boundary to the maximum bubble radius is sufficiently small (less than three) [37,38]. Because nanobomb activation in our experiments occurred at distances with significantly greater ratios – considering the bubble diameter of ≤4 µm [23], we do not expect significant boundary effects in our measurements. However, in the case of surface nanobomb’s activation, an interaction of bubbles with a surface could change their recondensation probability. Further, studies of bubble dynamics in elastic and viscoelastic media demonstrated that bubble dynamics can depend on mechanical properties of the surrounding medium [39,40]. A potential role of mechanical properties of the surrounding media on recondensation of nanobombs will be considered in our future studies.

We plan to initially apply nbOCE to studies of biomechanical changes in tissue associated with neoplasia. We showed that our method can reliably detect ∼30 kPa difference in stiffness between 10% and 11% PAA gel phantoms. This sensitivity is sufficient to detect biologically relevant differences in elasticity between normal and cancerous tissues including the following examples: normal breast tissue (28-30 kPa) and breast cancer (90-106 kPa) [41,42]; normal brain tissue (7.3 kPa) and meningiomas (33 kPa) [43]; and normal prostate tissue (16 kPa) and prostate cancer (40.6 kPa) [44].

Further, our nanobombs consist of perfluorocarbon (C5/C6) core and a phospholipid coating that are biocompatible materials. Indeed, perfluorocarbons are highly inert and non-toxic compounds [45–48] and they have been used in a variety of biomedical applications including blood substitutes [49–51] and in vivo imaging [52–54]. The phospholipid shell of our nanobomb is comprised of same lipids that are used in pharmaceutical liposomal drugs such as Doxil [55,56]. In addition, lipid-coated perfluorocarbon nanodroplets similar to our nanobombs are currently under investigation for photoacoustic and ultrasound imaging applications where they were shown to have a good biocompatibility [57–59].

Delivery of nanobombs for OCE applications in both in vitro and in vivo studies of biological samples is an important topic. Specifically, for studying mechanical properties in 3D cell cultures [60–62] the nanobombs can be mixed directly with the cell speroid/collagen mixture. We have already successfully used this method for two-photon excitation of perfluorocarbon nanodroplets in 3D cell cultures [23]. Since, nanobombs are made from inert and biocompatible materials they can be left in the culture for a prolonged period of time. We envision two potential ways for introducing nanobombs in vivo. First approach is a direct injection into the tumor/tissue with subsequent tissue diffusion. This approach was successfully used for administration of other nanoprobes and theranostic agents used for magnetic resonance, computed tomography, ultrasound, and optical imaging in vivo [63–66]. The second approach is based on a systemic intravenous injection and subsequent extravasation to the tumor because of the enhanced permeability and retention (EPR) effect [67–69]. This effect originates from fast and haphazard angiogenesis inside the tumors resulting in local blood vessels containing large gaps in their walls with sizes in the range of 100-1200 nm in size [70–72]. While EPR effect is not universal for all tumors, its validity is currently well established for variety of animal tumor models and is also utilized for delivery of liposomal drug formulations in the clinic (reviewed in [67,69]). The average size of nanobombs in 250-350 nm range (Table 1) makes them a good candidate for potential delivery using EPR effect.

In this study, we used the minimum surface fluence of 99 mJ/cm² which is just below the maximum permissible exposure (MPE) criterion for skin - 100 mJ/cm² [73]. Thus, future efforts will be focused on lowering laser fluence for nanobomb excitation to permit a safe transition from phantoms to in vivo studies. The pulse energy can be reduced as long as the signal to noise ratio (SNR) is similar to the measurements shown for example in Fig. 2(c) or Fig. 4(a), where the phase changes associated with shear wave propagation are 3 times higher than the phase noise. The SNR has a higher impact on detection of LSWs than the pulse energy as can be seen by comparing data obtained using 99 mJ/cm² (Fig. 4(i)-k) and 159 mJ/cm² (Fig. 4(i)). In our studies the activation of nanobombs was observed at ∼0.6 mm depth that is shallower than the estimated focal depth of 1.7 mm. This result indicates that the laser fluence at ∼0.6 mm was sufficiently high to induce nanobomb excitation. By shifting the focus of the excitation laser closer to the surface at ca. 0.5 mm depth, it might be possible to reduce the laser pulse energy for triggering nanobomb activation by as much as two orders of magnitude. This change requires adaptions of the current setup to shift the focus position of the swept source laser and the pump laser independently. The modifications of the optical setup will be carried out before future experiments, since the system has to be characterized and calibrated after introducing additional mechanical and optical components. In addition, the pulse energy can be reduced by increasing the dye loading in nanobombs.

5. Conclusion

In this paper, we demonstrated that multiple consequent laser excitations of dye-loaded PFC nanodroplets (i.e., nanobombs) can be used to generate highly localized LSWs and to estimate Young’s modulus using OCE. The energy from a nanosecond-pulsed laser was absorbed by the dye molecules embedded in the nanodroplets that triggered a liquid-to-gas phase transition of the nanoparticles. Subsequently, the nanobombs spontaneously recondensed and were triggered again by a consecutive laser pulse at 1 Hz (Fig. 1). OCE signals were continuously acquired to measure generation of LSWs and to calculate the wave speed. For C6 nanobombs, the measurements showed clear LSWs with good SNR up to fifty consequent laser pulses. Due to the strong displacement signal, it was possible to approximate Young’s moduli for repeated excitations on the same position and distinguish tissue phantoms with different stiffness.

Multiple repeated generations of LSWs by C6 nanobombs is a major improvement compared to our previous results [20,22]. Previously, we used C5 nanobombs made using perfluoropentane that has a lower boiling point compared to perfluorohexane used in C6 nanobombs. Laser activation of liquid-to-phase transition in C5 nanobombs was greatly diminished after consequent laser excitations. In contrast, the superior blinking properties of C6 nanobombs enabled robust repetitive excitations and multiple OCE measurements from a single spot in a sample of interest that opens up the possibility of implementing nanobomb OCE for longitudinal assessment of biomechanical properties of biological samples.

Funding

National Institutes of Health10.13039/100000002 (R01HL130804, 1R21CA231561, 2R01EY022362, R61AR078078).

Disclosures

The authors declare no conflicts of interest.