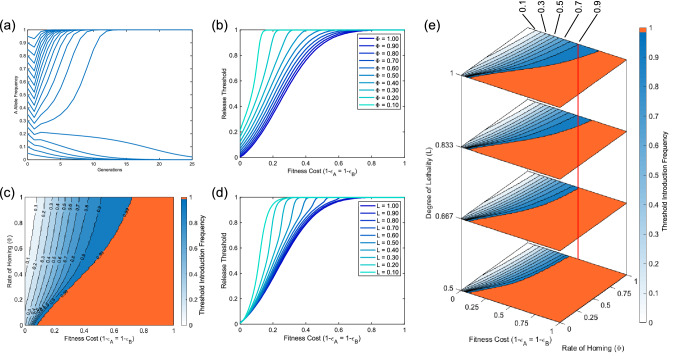
Figure 4.

SDKR displays threshold dependent behaviour that is affected by a range of parameters. Panel (a) shows sample numerical simulations demonstrating threshold-dependence of SDKR (with homing rate $\mathrm{\Phi }=0.9$, relative fitness $\epsilon =0.85$ and lethal penetrance $L=1$). Panel (b) demonstrates how the introduction threshold required for the system to spread (shown on the vertical axes) changes with variation in the rate of homing ($\mathrm{\Phi }$) and relative fitness ($\epsilon$) parameters with $L=1$. Similarly, (c) demonstrates the effect on required release thresholds but over the full range of possible homing rates ($\mathrm{\Phi }$) with $L=1$. Here an orange area denotes the parameter space in which the system gives a threshold introduction frequency $\ge$0.99 (i.e. where the system is unable to increase in frequency). Panel (d) demonstrates the effect of variation in relative fitness ($\epsilon$) and the degree of lethality conferred by the lethal effector from construct A—with homing rate $\mathrm{\Phi }=0.9$. Finally, panel (e) shows how initial release thresholds are affected over the full range of relative fitness ($\epsilon$) and homing rate ($\mathrm{\Phi }$) parameters as well as a selection of lethal penetrance parameters (L). Here the red line is included to aid visual distinction between the locations of contour lines. As in (c), here an orange area denotes parameter space where the system is unable to increase in frequency. Note that in each case we consider the release of individuals homozygous for both transgenic constructs and fitness costs that are applied multiplicatively.