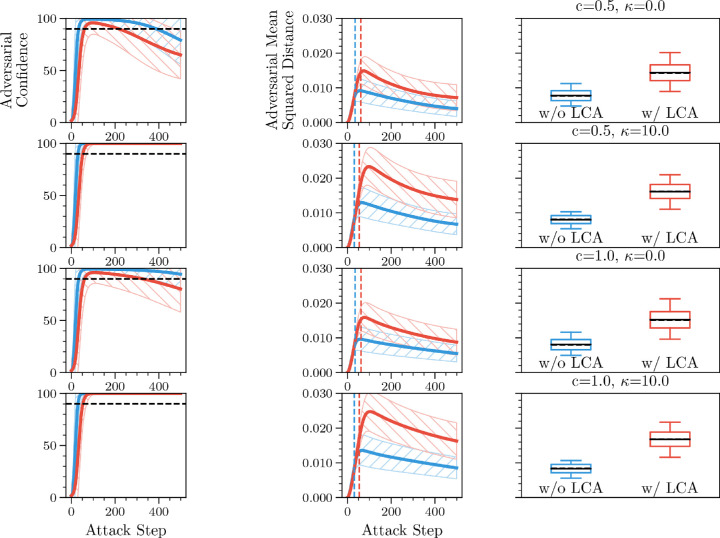
Figure A.6.

LCA network defends against an $l_2$ regularized attack. Carlini and Wagner (2017) describe a regularized attack (see also Equation (19)) that produces successful adversarial perturbations with a smaller $l_2$ distance than the standard gradient descent attack. The two columns are results when using different regularization constants, $c$, which trades off between adversarial confidence and perturbation size and $\kappa$, which encourages a certain degree of adversarial confidence. Each column shows: (Left) the w/ LCA model reaches the threshold adversarial confidence (black dashed line, 90%) after more steps than the w/o LCA variant. (Middle) LCA results in larger mean squared distances (MSDs) at most time steps. The colored vertical dashed lines show the time step when each model first reached the confidence threshold. (Right) A slice of the MSD at the time step when each model first reached the confidence threshold, with the same vertical axis scaling as the middle plot and plot details as in Figure 7. For the left two plots, the lines give the mean across all 10,000 test images and the hatched lighter region is the standard deviation.