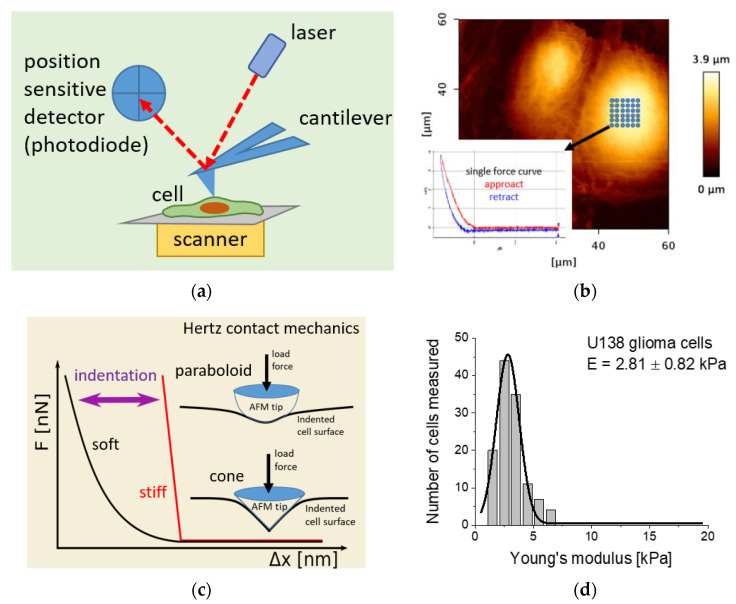
Figure 1.

(a) Illustration of the main elements constituting an atomic force microscope (AFM). (b) In the AFM-based elasticity measurements, a grid is placed over a central part of the cell. At each point, a so-called force curve is recorded (inset). (c) In nanomechanical analysis, the approach part of the calibration force curve (reference, curve acquired on a stiff, non-deformable surface) is subtracted from that measured on a cell. The obtained relation between the force and indentation is further used to calculate Young’s (elastic) modulus by applying Hertz contact mechanics with Sneddon modifications approximating the geometry of the probing tip. Typically, either a paraboloidal or a conical shape of the indenting AFM tip is considered. (d) The final Young’s modulus is frequently derived from a histogram by fitting Gauss or lognormal functions (exemplary results obtained for U138 glioma cells analyzed with Hertz–Sneddon mechanics, assuming a conical shape of the probing AFM tip).