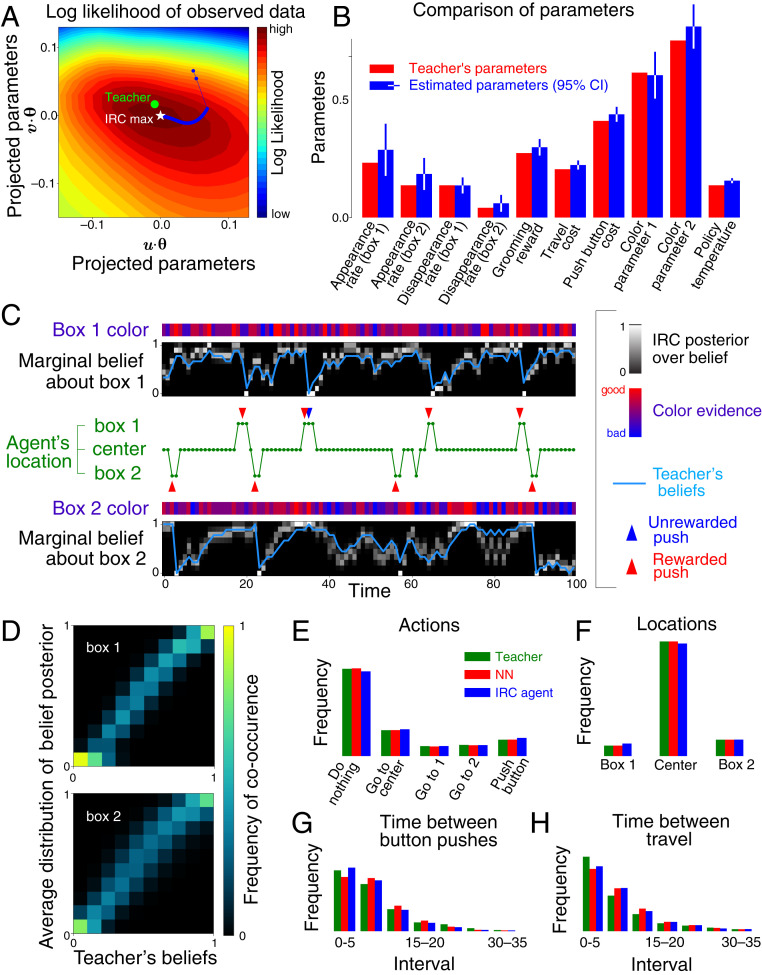
Fig. 3.

Successful recovery of agent model by inverse rational control. The agent was a neural network trained to imitate a suboptimal but rational teacher and tested on a novel task. (A) The estimated parameters converge to the optimal point of the observed data log-likelihood (white star). Since the parameter space is high-dimensional, we project it onto the first two principal components $\mathbf{u},\mathbf{v}$ of the learning trajectory for $\theta$ (blue). The estimated parameters differ slightly from the teacher’s parameters (green dot) due to data limitations. (B) Comparison of the teacher’s parameters and the estimated parameters. Error bars show 95% confidence intervals (CI) based on the Hessian of log-likelihood (SI Appendix, Fig. S2). (C) Estimated and the teacher’s true marginal belief dynamics over latent reward availability. These estimates are informed by the noisy color data at each box and the times and locations of the agent’s actions. The posteriors over beliefs are consistent with the dynamics of the teacher’s beliefs (blue line). (D) Teacher’s beliefs versus IRC belief posteriors averaged over all times when the teacher had the same beliefs, $\overline{p}=⟨p\left({\widehat{b}}_t|a_{1:T},o_{1:T}\right)|b_t⟩$. These mean posteriors $\overline{p}$ concentrate around the true beliefs of the teacher. (E–H) Inferred distributions of (E) actions, (F) residence times, (G) intervals between consecutive button-presses, and (H) intervals between movements.