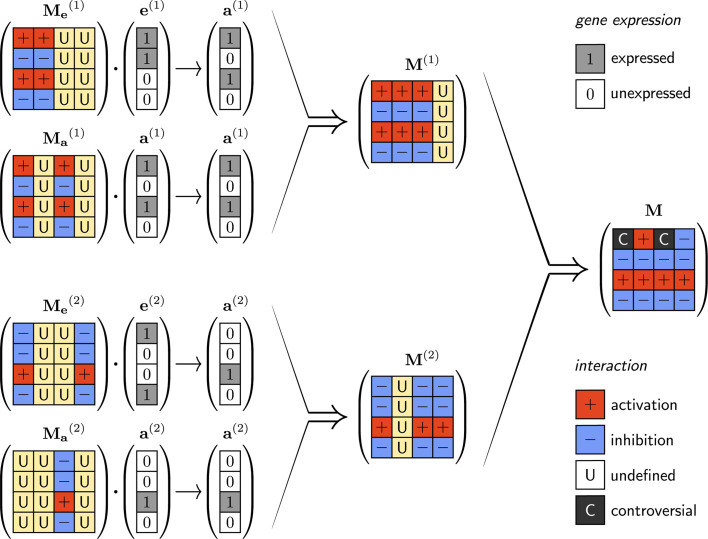
Fig 1. Illustration of the construction rules of interaction matrices based on theoretical considerations on the optimal pairwise interaction types between genes. e⁽¹⁾ and a⁽¹⁾ are the first embryo-adult pair, e⁽²⁾ and a⁽²⁾.

the second pair. Depending on the combination of gene expressions ${\mathrm{e}}_i^{\left(n\right)}$ and ${\mathrm{a}}_i^{\left(n\right)}$ in an embryo-adult vector pair (n = 1,2), an m_ij element of the interaction matrix can be positive (′+′, activation), negative (′−′, inhibition), or undefined (′U′). To ensure correct development $\left({\mathbf{M}}_{\mathbf{e}}^{\left(n\right)}{\mathbf{e}}^{\left(n\right)}\to {\mathbf{a}}^{\left(n\right)}\right)$ the ${\mathbf{M}}_{\mathbf{e}}^{\left(n\right)}$ matrices must have the structure indicated in the figure. (If $e_j^{\left(n\right)}=1$ and $a_i^{\left(n\right)}=1$, then $m_{ij}^{\left(n\right)}$ = ′+′; if $e_j^{\left(n\right)}=1$ and $a_i^{\left(n\right)}=0$, then $m_{ij}^{\left(n\right)}$ = ′−′; if $e_j^{\left(n\right)}=0$, then $m_{ij}^{\left(n\right)}$ = ′U′; irrespective of the value of $a_i^{\left(n\right)}$.) A similar argument holds for the stability criteria $\left({\mathbf{M}}_{\mathbf{a}}^{\left(n\right)}{\mathbf{a}}^{\left(n\right)}\to {\mathbf{a}}^{\left(n\right)}\right)$ and results in the ${\mathbf{M}}_{\mathbf{a}}^{\left(n\right)}$ matrices. By combining ${\mathbf{M}}_{\mathbf{e}}^{\left(n\right)}$ and ${\mathbf{M}}_{\mathbf{a}}^{\left(n\right)}$ the resulting M⁽ⁿ⁾ fulfills both the attractivity and stability criteria. The combination rules are the following: (+,+)→+; (−,−)→−; (±,U)→±; and (±,∓)→C, which can be done practically by taking the element-wise average of the two matrices. The ultimate combination of all M⁽ⁿ⁾s results in a matrix that fulfills the attraction and stability criteria for all different embryo-adult pairs.