Figure 2.
Parameterization and Analysis of a Temporal Model for Cell Contraction Signal Network Dynamics
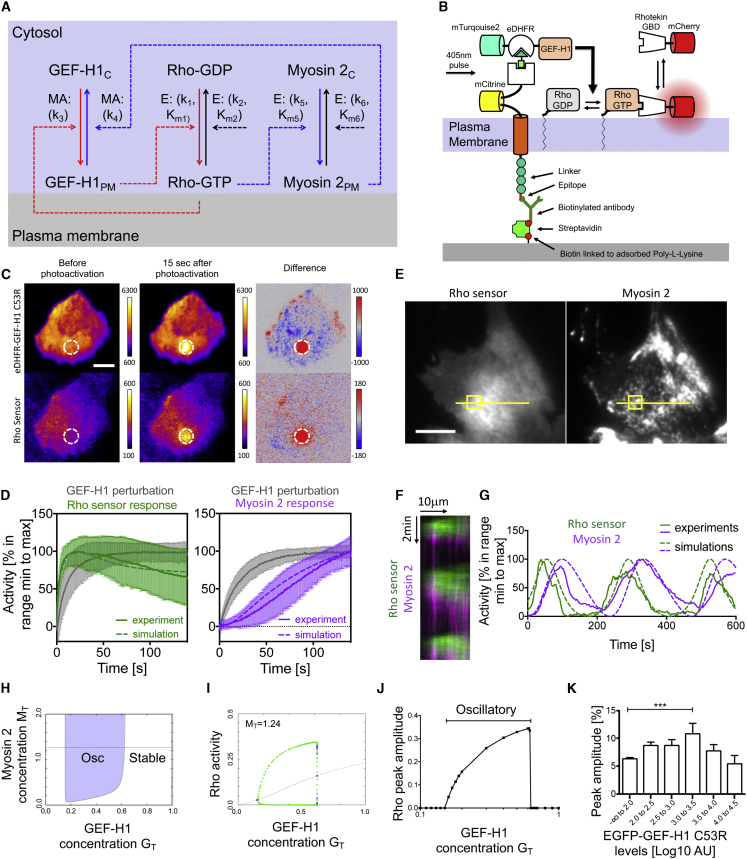
(A) A biochemical reaction scheme for positive and negative feedback regulation of Rho activity. GEF-H1 mediates positive feedback (highlighted in red) and myosin (non-muscle myosin-IIa, MYH9) mediates negative feedback (highlighted in blue). E, enzymatic reaction, MA, mass action, C, cytosolic, PM, plasma membrane-associated (a detailed description of the model and a justification of the specific implementation is given in Method Details).
(B) A schematic representation of improved molecular activity painting, a simplified, generic method for immobilized chemo-optogenetic plasma membrane recruitment and its application to introduce acute and stable GEF-H1 perturbations (see Method Details).
(C) TIRF images of immobilized GEF-H1(C53R) perturbation and Rho sensor response (see also Video S2).
(D) Kinetics of Rho activity sensor and myosin cell cortex recruitment response to acute chemo-optogenetic GEF-H1 perturbations and the corresponding numerical simulations of system dynamics using Equations 1, 2, and 3 (n ≥ 20 cells from at least 3 experiments, means and SEMs).
(E) TIRF images of U2OS cells, in which cytosolic GEF-H1 levels were increased by nocodazole-induced microtubule depolymerization (see also Video S3).
(F) Kymograph corresponding to the yellow line shown in (E) to visualize regular pulses of Rho activity followed by myosin cell cortex recruitment.
(G) Quantification of experimentally measured Rho activity and myosin cell cortex recruitment pulse dynamics corresponding to the yellow box in (E), and corresponding numerical simulations of system dynamics.
(H) Two parameter bifurcation analysis of Equations 1, 2, and 3 to predict total concentration ranges of the positive and negative feedback mediators GEF-H1 and myosin, which can generate stable or oscillatory system dynamics.
(I) One parameter bifurcation analysis of Rho activity dynamics predicts limit cycle oscillations at intermediate GEF-H1 concentrations (subcritical Hopf bifurcations at GT = 0.1557 and GT = 0.6215).
(J) Simulations of Rho activity dynamics predict maximal Rho activity peak amplitude at intermediate GEF-H1 concentrations.
(K) Experimental confirmation of maximal Rho activity peak amplitude at intermediate GEF-H1(C53R) expression levels (percentage of signal above background; n = 124 cells from 3 experiments; means and SEMs; ∗∗∗1-way ANOVA, Dunnett’s post test, p < 0.001).
Scale bars: 10 μm.
See also Figures S2 and S3.