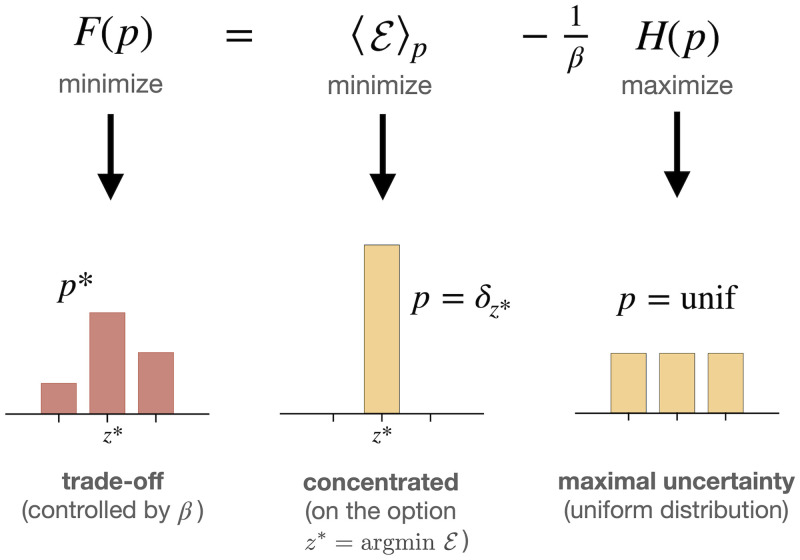
Fig 2. Minimizing the free energy from constraints (7) requires to trade off the competing terms of energy ${\langle \mathcal{E}\rangle }_p$ and entropy H(p), here shown exemplarily for the case of three elements.

Assuming there exists a unique minimal element $z^{*}={\text{argmin}}_z\mathcal{E}\left(z\right)$, then minimizing only ${\langle \mathcal{E}\rangle }_p$ over all probability distributions p results in the (Dirac delta) distribution δ_z* that assigns zero probability to all z_i ≠ z* and probability one to z_i = z*, and therefore has zero entropy. In contrast, minimizing only the term $-\frac{1}{\beta }H\left(p\right)$ is equivalent to maximizing H(p) and therefore would result in the uniform distribution that gives equal probability to all elements. The resulting Boltzmann distribution p* interpolates between these two extreme solutions of minimal energy (β → ∞) and maximum entropy (β → 0).