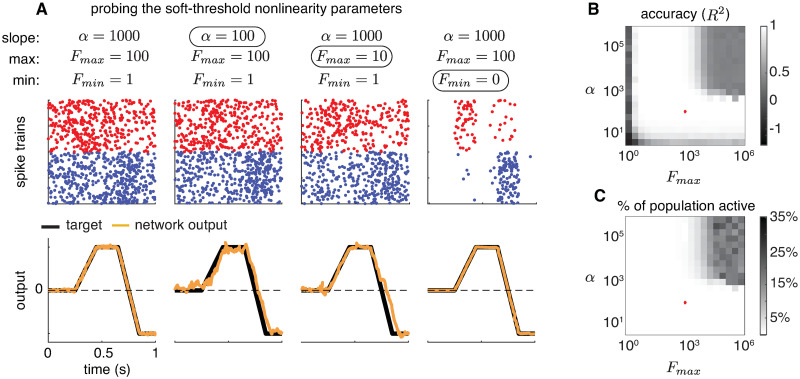
Fig 5.

(A) Simulations of local Poisson model showing the effects of varying the parameters of the soft-threshold nonlinearity on performance. Relevant parameters are the slope α, maximal firing rate F_max, and baseline firing rate F_min. Network dynamics implemented an exact 1D integrator and the stimulus was the same as Fig 2. Red and blue dots indicate spikes from neurons with positive and negative output weights, respectively. (B) Network performance as quantified by R² across a range of parameter settings with baseline fixed at F_min = 0 (log-scale). Red asterisk indicates the values for the rightmost column of A (α = 1000, F_max = 100). Accuracy remains high across a broad range of parameter values, falling substantially below 1 when slope and maximum firing rate are both large or very low. (C) Percent of the neural population active as a function of α and F_max, with F_m in = 0. The network shows ping-ponging behavior in upper right corner, where the model approaches a deterministic, hard-threshold firing rule.