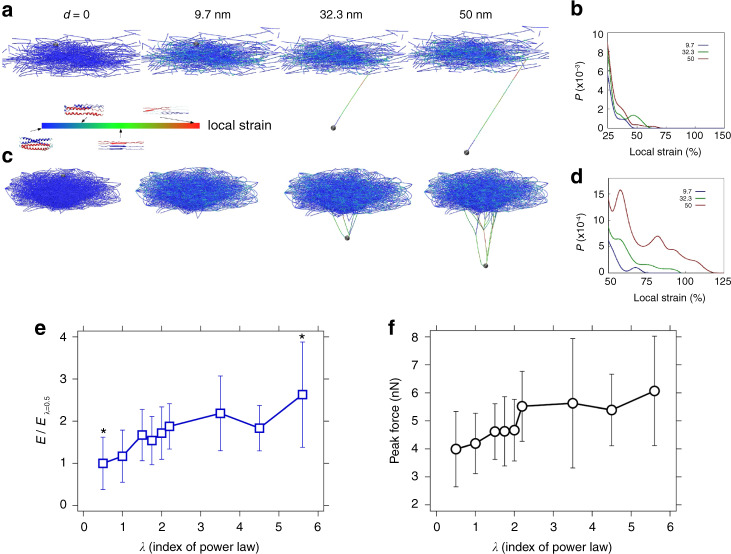
Fig. 6. Meshwork topology (λ) influences toughness and strength of lamin filaments.

Snapshots from simulations of mechanical pushing of single lamin filaments in meshworks of two different node connectivities: a λ = 0.5 (Supplementary Movie 1) and c λ = 5.6 (Supplementary Movie 2). The meshwork of λ = 0.5 was composed of many single filaments connected to a few heavy nodes, while the meshwork of λ = 5.6 was composed of well-connected filaments with a balance of light nodes, intermediate nodes and a few heavy nodes. The color scale denotes the local strain at different deformations, d, of the filament. b, d Probability distributions of the local strain within each filament segment measured at increasing deformations (corresponding to snapshots in panels a, c) for the two meshworks. At λ = 0.5, the filament being pushed ruptured from one end at an early stage (d < 32.3 nm), the other end was stretched and unraveled until the heavy node and the strain in the filament increased to cause rupture. At λ = 5.6, increasing deformation caused a large strain re-distribution. The meshwork with λ = 5.6 was associated with a much larger cohesive zone that enabled to dissipate more deformation energy before rupture (see “Methods”). Lamin filaments in meshworks with higher λ values were significantly e tougher (E) and f stronger as compared to filaments in meshworks with smaller λ. Comparing the values from λ = 0.5 and λ = 5.6 with a t-test yielded a p value of 0.05 denoted by *. Each mean value and standard deviation in e and f are obtained from FE curves of 100 independent simulations on networks of the same λ value, as summarized in Supplementary Fig. 18.