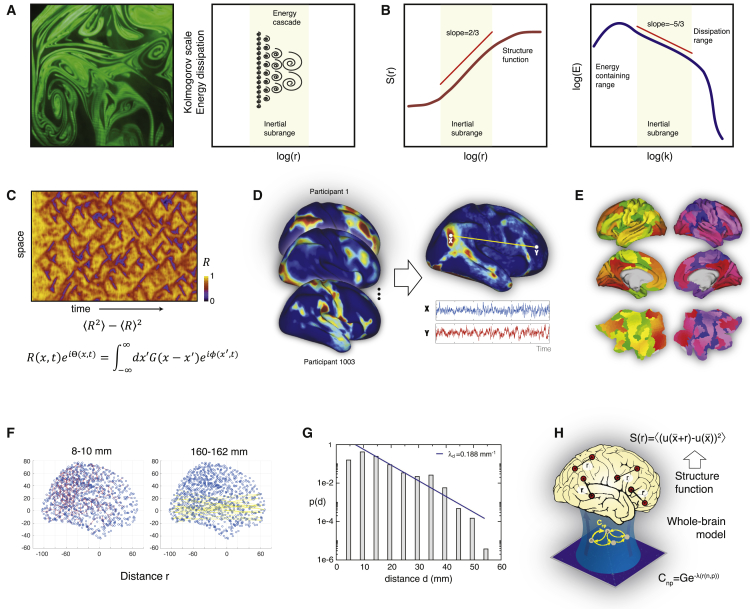
Figure 1.
Measuring Turbulence in Fluid Dynamics and in Human Brain Activity
(A) The study of turbulence in fluid dynamics was pioneered by Kolmogorov’s phenomenological theory of turbulence that is based on the concept of structure functions. In turn, it was inspired by Richardson’s concept of cascaded eddies. The left panel shows a snapshot of turbulence in a real physical system with different sizes of eddies, whose hierarchical organization is schematized for the inertial subrange in the right panel.
(B) In fluid dynamics, as shown in the cartoon, power laws are found in an inertial subrange where the structure functions show a universal scaling of (left panel) and an energy scaling of (right panel), where r is the spatial scale and k the associated wave number of the spectral scale. This power law behavior reflects the energy transfer cascade found in turbulence.
(C) Fluid dynamics can equally well be modeled by coupled oscillators, as shown by Kuramoto (1984). He defined a local order parameter, representing a spatial average of the complex phase factor of the local oscillators weighted by the coupling. The standard deviation of the modulus of this measure defines the level of amplitude turbulence, which is shown in the adapted figure for a ring of the Stuart-Landau oscillator system (Kawamura et al., 2007). This concept is not only valid for coupled oscillator modeling but also can be used to detect turbulence in a given system in a model-free way.
(D) Here, to detect the presence of turbulent-like human brain activity, we used state-of-the-art resting state data from a large set of 1,003 healthy human participants in the Human Connectome Project (HCP) database.
(E) We extracted the timeseries from each of the 1,000 parcels in the fine-grained Schaefer parcellation, which are shown here as slices in MNI space and on the surface of the HCP CIFTI (Connectivity Informatics Technology Initiative) file format space.
(F) The function structure is based on the functional correlations between pairs with equal Euclidean distance, r, in MNI space. Here, we show two examples of the pairs with r = 8–10 mm (left) and r = 160–162 mm (right).
(G) Most of the underlying brain connectivity follows the exponential decay described by the exponential distance rule (Ercsey-Ravasz et al., 2013). The figure shows the histogram of interareal projection length for all labeled neurons (n = 6,494,974) in a massive tract tracing study in non-human primates. The blue line shows the exponential fit with a decay rate 0.188mm−1.
(H) We used this anatomical basis in a whole-brain model based on Stuart-Landau oscillators (Deco et al., 2017), aiming to establish the causal mechanisms underlying the emergence of turbulent-like dynamics.