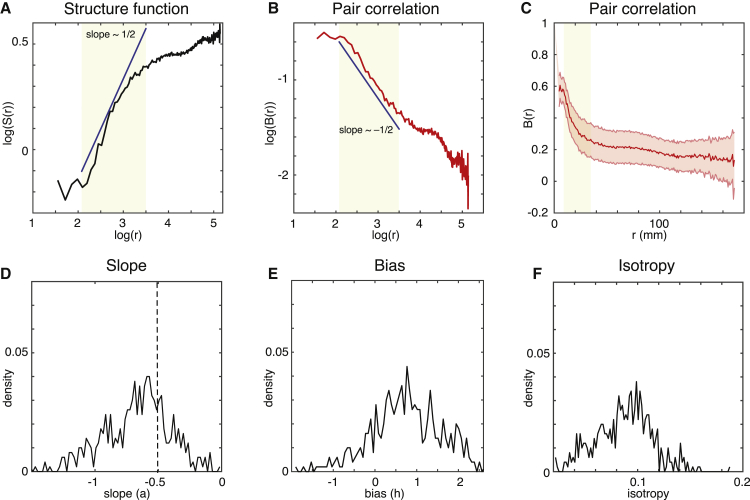
Figure 7.

Power Laws of the Functional Core

The figure demonstrates the presence of power law and homogeneous isotropy in the empirical human neuroimaging data from 1,003 participants.

(A) Spatial power scaling law of the structure function S(r) as a function of log(r) for the correlation function.

(B) Same spatial power scaling law for the correlation B(r) as a function of log(r).

(C) The correlation function B(r) as a function of the distance r, but showing the dispersion across regions (with the shadow indicating the standard deviation).

(D) The unimodal density distribution (across participants and node locations) of the slope parameter $a$.

(E) Similar unimodal density distribution of the bias parameter $h$.

(F) Unimodal density distribution of the mean (across r in the inertial subrange) of the standard deviation of B(r). These distributions are suggestive, but not proof, of turbulence and of a functional core of homogeneous isotropic function.