Connecting Longitudinal and Transverse Relaxation Rates in Live-Cell NMR

Abstract

In the cytosolic environment, protein crowding and Brownian motions result in numerous transient encounters. Each such encounter event increases the apparent size of the interacting molecules, leading to slower rotational tumbling. The extent of transient protein complexes formed in live cells can conveniently be quantified by an apparent viscosity, based on NMR-detected spin-relaxation measurements, that is, the longitudinal (T₁) and transverse (T₂) relaxation. From combined analysis of three different proteins and surface mutations thereof, we find that T₂ implies significantly higher apparent viscosity than T₁. At first sight, the effect on T₁ and T₂ seems thus nonunifiable, consistent with previous reports on other proteins. We show here that the T₁ and T₂ deviation is actually not a inconsistency but an expected feature of a system with fast exchange between free monomers and transient complexes. In this case, the deviation is basically reconciled by a model with fast exchange between the free-tumbling reporter protein and a transient complex with a uniform 143 kDa partner. The analysis is then taken one step further by accounting for the fact that the cytosolic content is by no means uniform but comprises a wide range of molecular sizes. Integrating over the complete size distribution of the cytosolic interaction ensemble enables us to predict both T₁ and T₂ from a single binding model. The result yields a bound population for each protein variant and provides a quantification of the transient interactions. We finally extend the approach to obtain a correction term for the shape of a database-derived mass distribution of the interactome in the mammalian cytosol, in good accord with the existing data of the cellular composition.

Introduction

The cell interior is an immensely complex and crowded environment, both in prokaryotic and eukaryotic cells. Hence, a freely diffusing protein is bound to undergo countless collisions and transient interactions with the surrounding macromolecules.¹⁻³ Most frequently, the collisions are nonelastic, that is, a transient, so-called, “encounter complex” is formed, allowing for Brownian-surface diffusion and a close-range search for putative specific recognition and binding. Preferably, such weak interactions may result in colocalization of functionally related proteins, often called the quinary structure,⁴⁻⁶ which can be described as a functional subset of all transient interactions. The duration of this surface search has been postulated to be under evolutionary optimization,^1,7,8 based on the argument that if the “hand shake” is too brief, the proteins may fail to recognize their partner and, conversely, if it is too long, they will simply waste their precious time. Consistent with this idea, the repulsive net-charge between cytosolic proteins across evolutionarily divergent organisms seems optimized for marginal colloidal stability.⁹ For a given protein, each encounter-complex formation results in a transient reduction in rotational and translational diffusion.¹⁰⁻¹³ The rotational component (D_rot) of this retardation is well-suited to be quantified by in-cell nuclear magnetic resonance (in-cell NMR). In essence, the rotational motions are here coupled to the longitudinal (T₁) and transverse (T₂) relaxation times¹⁴ that, in turn, provide a measure of a particular protein’s propensity to interact with the neighboring intracellular components.^6,10,11,15 The quantitative link between the molecular motions and the relaxation time is described by the overall correlation time (τ_c), which, in the general case, is the harmonic mean of global rotation (τ_r), local motions (τ_loc), and additional components such as chemical exchange (τ_ex): τ_c^–1 = τ_r^–1 + τ_loc^–1 + τ_ex^–1. The effects of the in-cell encounters on the molecular motions are expected to span several timescales and can be both global and local, but for folded proteins, the local motions are of less importance, that is, T₁ and T₂ mainly report on the rotational correlation time, τ_r.¹⁶

Previous studies have shown that the extent of D_rot retardation upon cell internalization depends not only on the protein’s physicochemical surface properties^6,10,11,17 but also on the type of host cell.^10,11,13 This in-cell retardation is manifested as increased T₁ and decreased T₂ relaxation times^11,14,18,19 (Figure 1, Supporting Information 1), where most commonly T₂ has been exploited to quantify the retardation effect, both directly by determination of the relaxation time^10,11,19 and indirectly through line-broadening analysis.^6,20

Figure 1.

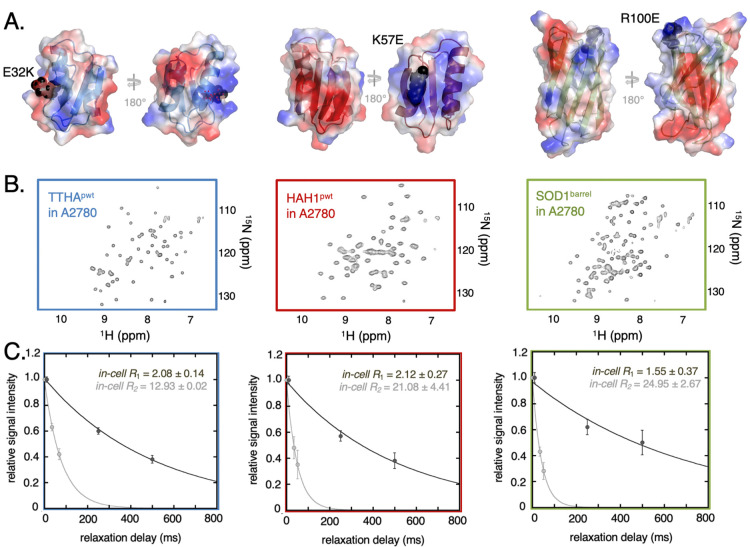
Probe proteins in-cell NMR properties and relaxation. (A) shows the proteins TTHA^pwt (blue), HAH1^pwt (red), and SOD1^barrel (green) including secondary structure elements. The electrostatic surface of each protein is displayed, with blue-colored patches belonging to the basic, positively charged residues arginine or lysine and the red colored patches belonging to the acidic, negatively charged residues glutamate or aspartate. The surface charge mutations are highlighted as black spheres. (B) depicts HMQC spectra of the reporter protein electroporated into live A2780 cells. (C) In-cell NMR relaxation data of the three basis reporter proteins are shown. Signal intensity attenuation obtained from the R₁ (dark gray) and R₂ (light gray) experiments are shown as filled circles and the corresponding fitted single exponential fits are shown as solid lines. The error bars in the relaxation rates are estimated from the signal-to-noise-ratio in each experiment (Supporting Information Methods).

To enable comparison of proteins with different mass, we translate here the observed relaxation times into “apparent viscosities” (η^app),^11,13,20,21 that is, the microscopic viscosities that yield the same relaxation parameters as observed in cells.¹⁰ The η^app values are derived from the reference curves, in which T₁ and T₂ are determined for each protein in increasing amounts of glycerol with well-defined viscosities. Even so, this mean-field approach results in an apparent disagreement between T₁ and T₂ in-cell relaxation times, where transverse relaxation reports on much higher η^app than longitudinal relaxation.

To pinpoint this T₁ and T₂ inconsistency, we expand here the mean-field retardation approximation to a binding model, where the reporter protein is set to be in fast exchange between a free monomeric state and a bound state with a cellular partner. This partner is, in the simplest case, a protein of uniform size or a distribution of proteins with different sizes. As a result, the observed T₁ and T₂ values for our three different proteins and their mutants can be accounted for by a single model. Our basic observation is that the relaxation data features can be accurately described by the minimal assumption of a single partner of uniform size. This accuracy is retained upon accounting for more realistic partner-mass distributions. The best partner-mass distribution is that obtained from the naturally occurring cytosolic proteins but with an increased tail of higher mass species. Consistent with the cellular composition, this tail is suggested to report on transient interactions with higher order complexes and larger biomolecular structures, such as membranes and ribosomes. Thus, by accounting for the full distribution of putative interaction partners, we are allowed to connect the rotational retardation to the fraction of transiently bound reporter proteins, p_B. This bound population constitutes also a quantitative link between the reporter protein properties and their interaction pattern in cells. A final implication of this result is that information about the particular partner-size distributions under a given set of conditions can be obtained directly from T₁ and T₂, providing a new handle for exploring the macromolecular machinery at work in live cells.

Experimental Procedures

Protein Mutagenesis, Expression, and Purification

Plasmids were transformed into Escherichia coli BL21(DE3) expression strains, and point mutations were introduced through site-directed mutagenesis. For ¹⁵N-isotope-enriched protein production, minimal medium [0.02 M KH₂PO₄, 0.04 M Na₂HPO₄, 0.1 M NaCl, 2 mM MgSO₄, 0.4% (w/v) glucose, and trace metals (1 mM MgCl₂, 15 μM CaCl₂, 1 μM FeSO₄, 32 nM AlCl₃, 33 nM CoCl₂, 12 nM CuSO₄, 120 nM KI, 100 nM MnSO₄, 4 nM NiSO₄, 16 nM Na₂MoO₄, 15 nM ZnSO₄, 5 nM KCr(SO₄)₂, 15 nM H₃BO_4, and 100 μM citric acid), pH 7.0] supplemented with carbenicillin and 0.1% (w/v) ¹⁵NH₄Cl was inoculated and grown at 37 °C until OD₆₀₀ = 0.6–0.8. Isopropyl β-d-1-thiogalactopyranoside (IPTG) (0.5 mM) was added for 4 h overexpression. Cells were harvested at 5000g for 10 min at 4 °C (Supporting Information Methods). Protein purification of SOD1^barrel is described in detail by Danielsson et al.,²² while detailed protocols for TTHA^pwt and HAH1^pwt are described by Mu et al.(6) and Leeb et al.(10)

Protein Transfer into Mammalian Cells for In-Cell NMR

Cell growth and protein transfer by electroporation were as described in the literature.¹⁰ In short, human ovary adenocarcinoma A2780 cells were grown to 70–90% confluence. Approximately, 60 × 10⁶ cells were suspended and supplemented with the respective reporter proteins to 1.5 mM final protein concentration. Electroporation was conducted by 115 V, 14–16 ms poring pulses followed by 5 × 50 ms transfer pulses at 20 V. After electroporation, the cells were washed, plated, and left for 5 h recovery. Then, the live cells were transferred to a 4 mm flat-bottomed NMR tube (BMS-004B, Shigemi Inc., Tokyo, Japan) (Supporting Information Methods).

In-Cell Relaxation Measurements

All NMR data were acquired on a Bruker AVANCE III 700 MHz spectrometer with a cryogenically cooled triple-resonance probe. All experiments were performed at 37 °C using an “interleaved” acquisition method.¹⁰ Both R₂ and R₁ measurements were carried out using one-dimensional ¹⁵N-filtered heteronuclear single quantum coherence (HSQC)-based pulse sequences with three relaxation delays each, ranging between 0 and 68 ms in the case of R₂ and 10 and 500 ms in the case of R₁.

Quantification of Protein Leakage

Leakage of the reporter protein into the interstitial fluid surrounding the cells was quantified by carefully removing the cell slurry from the NMR tube. After spinning 5 min at 200 g, the supernatant was transferred to a fresh NMR tube and 1D ¹H-SOFAST–HMQC was recorded (Figure S2). Integrating over the same spectral regions in both samples and then calculating the ratio after correcting for dilution in the supernatant samples showed that protein leakage typically is less than 10% (Figure S2). In addition, there is evidence that most of the leakage is introduced during sample preparation of the supernatant.⁶

Relaxation Measurements of In Vitro Glycerol Series

200 μM protein, 10 mM MES pH 6.5, 10% (v/v) D₂O, and increasing amounts of deuterated glycerol-d₈ (98% D) from 0 to 50% (v/v) were used. Both R₁ and R₂ were determined with 6–10 relaxation delays (Supporting Information Methods). Data was finally analyzed using MATLAB (MathWorks, MA, USA) scripts as described in the literature.¹⁰

Lysozyme Crowding

100 μM TTHA^pwt, 20 mM MES pH 6.5, and 10% (v/v) D₂O together with 50 or 150 mg/mL human lysozyme (Sigma-Aldrich) were used. Both R₁ and R₂ were determined using 5–6 relaxation delay times. Data was analyzed with in-house MATLAB (MathWorks, MA, USA) scripts. Since lysozyme is pH-active, the sample pH had decreased to 6.0 and 5.6 for 50 and 150 mg/mL, respectively. Fluorescence spectroscopy was conducted under similar conditions, where 0–20 mM TTHA^pwt was titrated onto 100 mM human lysosome, upon which the induced change in intrinsic tryptophan fluorescence from lysozyme was detected (Figure S5).

Curating and Analyzing the Cytosolic Proteome Database

The proteomic composition of the mammalian cytosol was estimated from the database by Geiger et al.,²³ where lysate proteins of eleven human cancer cell lines were quantified by mass spectrometry. Of the 11,731 proteins in the Geiger list, 4.2% were given ambiguous UniProt-IDs, and these sequences were omitted. The calculations of charge density of the proteins are described in the Supporting Information Methods.

Results and Discussion

Model System

Quantification of NMR relaxation in live mammalian cells requires good signal to noise data. This means that the proteins used must exhibit only weak interactions with the surroundings as extensive interactions lead to severe line-broadening.⁵ We use here three well-characterized model proteins: (i) the nonmetal binding variant of the putative heavy-metal binding protein TTHA1718 from Thermus thermophilus (TTHA^pwt),⁶ (ii) the corresponding de-metalated variant of the copper chaperone HAH1 (HAH1^pwt),⁶ and (iii) the loop-truncated variant of the human superoxide dismutase SOD1 (SOD1^barrel)²² (Figure 1). TTHA^pwt and HAH1^pwt are structural homologues, but with distinct surface properties, making them well suited as reporter proteins for surface-mediated interactions in cells. All three proteins exhibit good NMR-relaxation properties in live mammalian cells,¹⁰ where well-resolved HMQC spectra (Figure 1) indicate that they only diffusely interact with the cell interior.^10,24 That is, they mainly probe nonspecific transient encounters. Nonetheless, in previous studies, we have shown that these three proteins exhibit different degrees of transient interactions related to their surface properties. Of particular importance here is the surface net-charge density and surface hydrophobicity.^6,10 To expand the surface-property space, we included further three surface variants of the model proteins above, all of which alter the surface net charge by 2 units: a Glu to Lys substitution on the TTHA^pwt background (TTHA^E32K), a Lys to Glu substitution on the HAH1^pwt background (HAH1^K57E), and an Arg to Glu substitution on SOD1^barrel (SOD1^R100E) (Figure 1). This set of six proteins then serves as reporters on the transient interactions between the protein surfaces and the cellular surroundings. For the in-cell NMR measurement, the proteins were electroporated into A2780 cells, obtaining approximately 20 μM intracellular concentration,¹⁰ corresponding to approximately 10 μM total sample concentration.

Longitudinal and Transverse Relaxation Report Different Apparent Viscosity in Human Cells

To quantify the mean-field parameter, η^app, we determined the global ¹⁵N R₁ = T₁^–1 and ¹⁵N R₂ = T₂^–1 of all six proteins in live A2780 cells at 37 °C¹⁰ (Figure 1, Table 1, Figures S1 and S2). Hereinafter, we will use the relaxation rate (R_i) in parallel to the relaxation time (T_i), for clarity in the analysis. Due to the relatively low total concentration of isotope-labeled reporter protein in the cell sample and the limited life time of the cells in the NMR tube,²⁵ we were only able to record three relaxation delay times (Figure 1), where we integrate over a set of amide signals (Supporting Information Methods). The interscan delay was set to 1 s, which is bordering on being too short for the R₁ relaxation rates of 1.5–2 s^–1. As a possible consequence of this trade-off between interscan relaxation delay and the total experimental time, the R₁ data shows some deviation from ideal mono-exponential behavior, most evidently for the shortest delay (Figure 1). In addition, a contributing factor to the deviation from single exponentiality could stem from the presence of two populations of the reporter protein–cytosolic and leaked protein. However, the leakage is in most cases negligible, no systematic deviations are found in the R₂ attenuation curves (Figure 1), and no correlation between the magnitude of deviation and the amount of leakage can be observed. Furthermore, fitting the data to a biexponential yielded nonphysiological relaxation values (Figure S3). Taken together, we conclude that leakage is not a major contributing factor to the deviation from monoexponentiality.

Table 1. Collected Physicochemical Properties and In-Cell Relaxation Rates of the Reporter Proteins in Human A2780 Cells.

Protein	Mw (Da)	net chargea	R1	R2b
TTHApwt	7009	–1.47	2.08 ± 0.14	12.93 ± 0.02
TTHAE32K	7008	0.50	1.96 ± 0.50	22.62 ± 2.26
HAH1pwt	7353	0.94	2.12 ± 0.27	21.08 ± 4.41
HAH1K57E	7354	–1.08	2.04 ± 0.29	11.76 ± 1.56
SOD1barrel	10962	–0.70	1.55 ± 0.37	24.95 ± 2.67
SODR100E	10949	–2.50	1.74 ± 0.31	16.63 ± 2.26

^aNet charge calculated using propKa 3.0.⁵⁰

^bData from Leeb et al..¹⁰

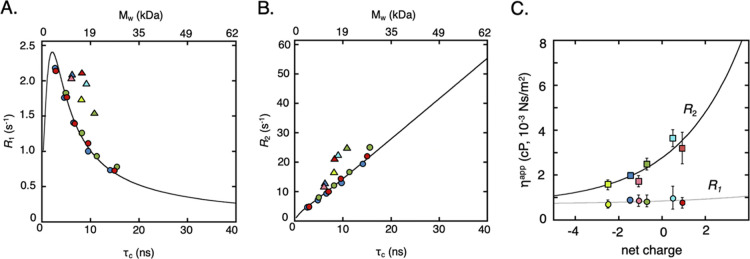
To test the reproducibility, we determined R₁ of HAH1^pwt twice, with R₁ = 2.12 ± 0.27 and 2.09 ± 0.18 s^–1, indicating the precision of the relaxation measurements. R₂ precision has previously been shown to be similar.¹⁰ We compared the R₁ and R₂ values to reference values obtained in water–glycerol mixtures to get η^app (Supporting Information 2, Figure S4, Table S1). As expected from previous work,^6,10,11 the results show that the R₂-derived η^app values increase with increased protein net-charge (Figure 2, Table 2, Figure S4). This complies with the notion that the more positively charged the proteins are, the more strongly they interact with the intracellular environment.^{6,10,11,17,26−29} It is further apparent that the R₁-derived η^app values are much less affected (Figure 2) by showing lower apparent viscosity as well as nearly no charge dependence. Using the R₂-derived η^app to predict the corresponding R₁ values results thus in poor agreement with the observed values (Figure 3), with high rmsd = 4.86 and low Pearson correlation coefficient r² = 0.23 between the measured and calculated relaxation rates. Nonetheless, the observation that R₁ and R₂ yield different η^app is in good agreement with previous findings.^11,19 From ¹⁹F NMR relaxation analysis, this discrepancy has been suggested to stem from ¹⁹F R₂ being more sensitive to transient interactions, while ¹⁹F R₁ reports mainly on local motions.¹⁹ Basically, this shows that this mean-field approach at some level fails to fully describe the in-cell effect. For comparison, ¹⁵N R₁ and ¹⁵N R₂ of the same proteins in glycerol–water mixtures fall well within the theoretical predictions (Figure 2, Supporting Information 1, Table S1).

Figure 2.

NMR relaxation data and apparent viscosity derived therefrom. (A,B) NMR relaxation rates as functions of rotational correlation time, τ_r, and molecular weight M_w, at 700 MHz (16.5 T) field strength. The colored circles are the measured relaxation rates [(A) R₁, (B) R₂] for the three proteins (HAH1^pwt: red, SOD1^barrel: green and TTHA^pwt: blue) in increasingly viscous glycerol solutions. While τ_r values calculated from the two relaxation rates (Supporting Information 1) fit the predicted theoretical values (black line) in the case of the in vitro glycerol data, clear deviations from the theory are found for the in-cell relaxation data (triangles), where the brighter colors correspond to the respective surface mutation. (C) Apparent viscosities η^app derived from transverse, R₂ (squares), and from longitudinal in-cell relaxation, R₁ (circles), plotted against protein net charge, where the colors are as in (A,B). The lines are empirically fitted exponential curves, with an offset corresponding to the intrinsic viscosity of water.¹⁰ The marked discrepancy between the obtained η^app values suggests that the mean-field η^app model is insufficient for explaining changes in NMR relaxation due to intracellular encounters.

Table 2. Apparent Viscosities η^app Derived from F_R1and F_R2.

protein	ηapp,R1 (cP)a	ηapp,R2 (cP)
TTHApwt	0.86 (−0.12, +0.10)	2.02 ± 0.00
TTHAE32K	0.96 (−0.48, +0.54)	3.64 ± 0.38
HAH1pwt	0.78 (−0.26, +0.21)	3.20 ± 0.70
HAH1K57E	0.84 (−0.24, +0.26)	1.72 ± 0.25
SOD1barrel	0.81 (−0.23, +0.29)	2.48 ± 0.26
SOD1R100E	0.68 (−0.16, +0.21)	1.56 ± 0.22

^aIn the case of R₁-derived η^app, the error is asymmetric and are shown in parentheses.

Figure 3.

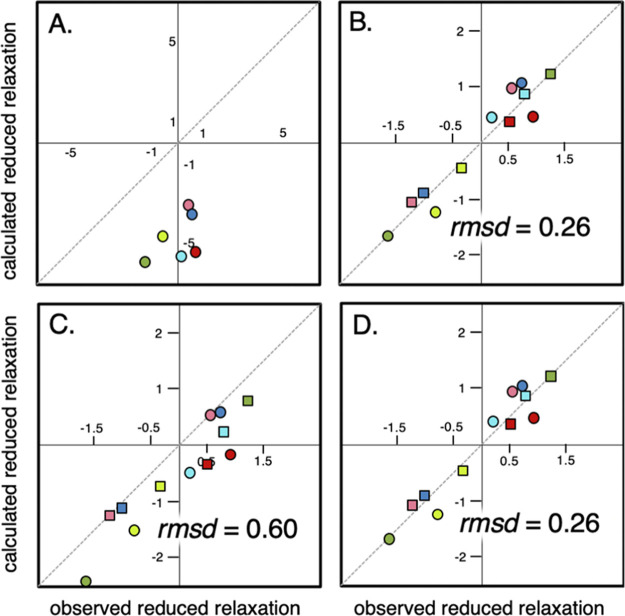
Agreement between observed and calculated reduced relaxation rates for the different models. The calculated R₁ = T₁^–1 values in (A) are from the mean field η^app approach, note the different axis scale in this figure. (B) Corresponds to fast exchange to a binding partner with an optimized mass of 143 kDa. In (C, D), lognormal mass distributions are used, where the shape factors are optimized in (D). The dashed line corresponds to a 1:1 correlation. Reduced R₁ values are shown as circles, while reduced R₂ values are depicted as squares. The color coding is the same as in Figures 1 and 2.

One explanation for the observed discrepancy is that the intracellular environment, in contrast to glycerol, adds chemical-exchange contributions from local surface interactions. R₂ is here known to be most affected through exchange broadening (R_ex),^30,31 while R₁ is left relatively unaffected. Challenging this idea, we have previously found that with our reporter proteins, the cytosolic enhancement of R₂ is largely due to changes in global rotation, τ_r.¹⁰ In essence, our conclusion is based on the finding that the line-broadening effect in the in-cell NMR spectra is uniform over all residues,¹⁰ suggesting that the effect is global retardation rather than localized exchange effects. The effect on R₂ is, moreover, independent of the nuclei type, which would not be the case if R_ex would be the dominating factor. Finally, removal of the refocusing CPMG train in the pulse sequence of the R₂ experiment¹⁰ renders very similar relaxation rates, which suggests relatively small R_ex contributions in the ms regime. Taken together, these observations indicate that exchange processes are not the primary cause for discrepancy in the observed in-cell relaxation effects and that an alternative explanation is to be found.

Transient Binding to a Single Large Partner Reconciles R₁ and R₂ Data

To seek a model that predicts both R₁ and R₂, we first extended the mean-field assumption where the tumbling of the entire protein ensemble is affected homogenously to a model where free monomers, with mass M_j, are in rapid exchange with transient clusters of an average molecular weight M^av (Supporting Information 3). This extension yields a population-weighted average of the relaxation rates of the bound and free state according to

1

where p_B is the fraction of reporter protein bound to the cluster at any given time and F_Ri is the closed-form expression of the relaxation rate as a function of mass (Supporting Information 1). The good in-cell NMR properties of the proteins¹⁰ indicate that the fast-exchange criterion holds since long-lived binding would yield line-broadening beyond the detection limit.⁵ This model constitutes a simplified description of the transiently bound state: the encounter complex is pictured as a rigid body with mass M_j + M^av. However, a formed encounter complex involves Brownian motion along the complex surface, which also affects relaxation. The assumption of a rigid complex may thus result in a slight underestimation of p_B. In this analysis, we assume that the correlation time is independent of the direction and that the diffusion tensor is symmetric. Although the former simplification breaks down in highly concentrated heterogeneous environments, the relatively small effects on the relaxation properties of the reporter proteins in A2780¹⁰ suggest a comparably diluted environment. Use of a set of relaxation rates of individual spins located over the structure would allow the determination of the diffusion tensor.³² However, here, we determine an average relaxation rate from many amide spins, spread out over the structure, justifying the use of an isotropic diffusion tensor. The near-linear dependence between R₂ and molecular mass (Figure 2) means that any encounter complex mass can be accounted for by adjusting p_B, while, in contrast, the nonlinear relationship between R₁ and mass (Figure 2) strongly confines the possible masses of the complex, fixating p_B. To benchmark this approach for quantifying weak transient interactions, we determined the effect on the relaxation rates of TTHA^pwt, in presence of 50 and 150 mg/mL human lysozyme-concentrations comparable with the total protein levels in human cells.^10,33 Here, we find that R₁ and R₂ agrees well with a 1:1 weak transient complex for p_B = 0.25 and 0.46 respectively, in good accordance with fluorescence-detected binding affinity (Supporting Information 4, Figure S5).

As shown in Figure 3, the introduction of a bound species with a common interaction partner of M_av = 143 kDa in addition to the free monomer accounts well for the in-cell R₁ and R₂ values of all six protein variants (Table S2). To assure that we get the same statistical weight for both R₁ and R₂ data in the fitting procedure, we use reduced relaxation parameters according to

2

where j denotes reporter protein j, i = 1 || 2, brackets denote the average over the full dataset (e.g. all R₂ values), and σ is the standard deviation of the dataset. The correlation between the observed and calculated R₁ now approaches a unit line with r² = 0.93 and rmsd = 0.26 (Figure 3). That is, the in-cell effect can indeed be described by alterations of τ_r alone, without the need to invoke additional chemical-exchange contributions. Furthermore, this shows that both R₁ and R₂ can be reconciled in a model where all proteins “feel” the same interaction environment and where the sole difference is the bound fraction. Intriguingly, and somewhat surprisingly, all reporter proteins show relatively low p_B values (Table S2) despite being in the crowded cytosol. Still, the inert, soluble, and, mainly, negatively charged reporter proteins are expected to be kept soluble by charge repulsion with the negative surroundings, reducing the amount of potential complex-forming contacts.⁹ Further, also in the presence of high concentration of the positively charged lysozyme, the negatively charged TTHA^pwt shows low p_B, confirmed by fluorescence experiments (Figure S5), which underlines the low interactivity of this protein. Furthermore, the excellent quality of all the reporter proteins’ in-cell NMR spectra indicates a low p_B, as a highly populated complex of high molecular weight would yield a significant increase in R₂ if substantially populated (Figure 2).

To further test this result, we examined next how well the value of M^av = 143 kDa actually agrees with the various sizes of transient complexes expected to be formed in the cell. As a base for comparison, we used all human proteins in the UniProt database³⁴ annotated as cytosolic (Supporting Information Methods). The protein-mass distribution of this data set complies with both Γ- and lognormal distributions,³⁵ where the latter gives a somewhat better fit (Figure 3).

Notably, the employed protein-data set yields no information of abundance, which might bias the distribution. To test for such bias, we used an alternative data set from Geiger et al.,²³ listing the individual sequences and relative abundance of lysate proteins from several mammalian cancer cell lines. The result shows that the abundance-weighted distribution agrees well with the original cytosolic subset from the UniProt database (Supporting Information Methods, Figure S6). On this basis, we stick to the lognormal distribution from the cytosolic subset as an estimate for the interaction partner protein mass distribution, yielding an average protein mass of M^av = 73 kDa. Upon lowering the mass in eq 1 from M_av = 143 kDa to M^av = 73 kDa, however, the agreement with the observed relaxation data becomes compromised (Supporting Information 3, Table S2). The reason why the 143 to 73 kDa decrease cannot simply be compensated for by a higher population of bound species is due to the distinct mass dependence of R₁ and R₂ (Figure 1): for a given molecular mass of the transient complex, a change in bound population to fit one type of in-cell relaxation will inevitably lead to a coupled change in the other and concomitantly to a mismatch in most cases.

Approaching a Physiologically Relevant Situation

Even if we can reconcile both types of relaxation with a two-state binding model, a uniform protein mass does not realistically describe the in-cell situation. To better account for the natural protein-mass heterogeneity, we developed the model to include not only the encounters with a single average partner but with a distribution of species matching the cytosolic protein sizes. A set of putative binding partners were obtained by integrating over the full mass distribution of cytosolic proteins. This allows us to obtain the mass-weighted relaxation rates of the protein-encounter complexes (eq 2). Notably, the fast-exchange model in eq 1 relies on the assumption that the reporter protein is equally likely to collide and interact with all molecules in the distribution. Hence, as the surface properties are crucial for interaction and encounter formation,^6,10,17 the net-charge density of different intervals in the mass distribution must overlap. As a control, we divided the distribution into three size regimes, that is, <70, 70–140, and >140 kDa, and calculated the net-charge density⁹ (Supporting Information 5). The result confirms that the surface-charge distribution of the three subensembles indeed overlaps nicely (Figure S7). This uniform mass–charge relation allows us to include the full distribution of binding partners in the fast exchange model described in eq 1, where the relaxation rate of the bound state now is given by

3

where ρ(M_w) is the size distribution of interaction partners and F_Ri(M_j + M_w) is the closed-form expression for the relaxation rate for a complex between protein j and a binding partner with mass M_w (Supporting Information 3). Optimization of the bound population (p_B) for each reporter protein using eqs 1 and 3 and integration over the database-derived lognormal ρ(M_w) (Figure 3, Table S2) improve the agreement between observed and calculated R₁ values, compared to the single average mass of the cytosolic proteins. Yet, the lower r² = 0.87 and rmsd = 0.60, together with the systematic underestimate of calculated R₁, indicate that the distribution of masses of the cytosolic proteins remains shifted towards too small proteins to account for the observed in-cell retardation.

Accounting for Larger Cellular Complexes in the Size Distribution Finally Reconnects the T₁ and T₂ Relaxations

Internalized proteins encounter not only other monomeric proteins but interact also with larger cellular components. Although a diffusing protein is most likely to collide with other proteins, simply because of their large proportion of the cellular dry weight,^36,37 it will also encounter other macromolecular structures and surfaces of larger dimensions. Examples of such structures are the cytoskeleton, membranes, and ribosomes. The amount of transient interactions is mainly determined by the overall macromolecular concentration and surface properties of the interacting molecules,^6,10 where the surface charge seems to be a key determinant. To a first approximation, the surface-charge density of the larger cellular structures can be assumed to follow the same distribution as the cytosolic proteins (Figure 4). Most clearly, the cytoskeleton is primarily composed of tubulin, actin, and lamin, all of which show similar net negative surface charge density as soluble proteins. The surface architectures of membranes and ribosomes, however, are partly distinct from proteins and need extra consideration. Mammalian membranes are dynamic bilayers, where the fraction of anionic lipids is between 10 and 30%.^38,39 This translates to a surface net charge of −0.15––0.45 e/nm², which is somewhat more negative than for the average protein (−0.065 e/nm²). Considering also the presence of ∼1/10 nm² integral membrane proteins⁴⁰ with a positive-inside orientation^41,42 and that the lipid bilayer also consists of nonlipid, noncharged alcohols such as cholesterol, the effective surface charge density can still be assumed to fall in the same range as protein surfaces. Ribosomes are highly negative, abundant megadalton entities,^43,44 where the high surface charge density places ribosomes in the negative tail of the net charge distribution (Figure 4). Nonetheless, even in this case transient interactions seem to follow a similar net charge dependence as protein–protein interactions,^6,10,12 where positively charged proteins even form semistable complexes with ribosomes.^12,45 Indeed, for several proteins, the observed line broadening in in-cell NMR experiments has been assigned to mainly stem from transient ribosome interactions.^46,47

Figure 4.

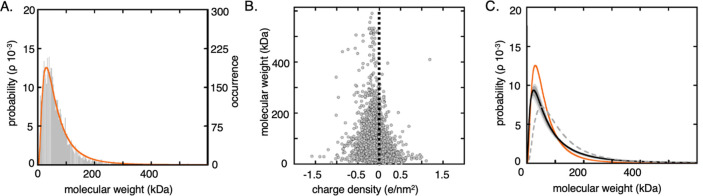
Size distribution estimated from in-cell relaxation data agrees well with the database-derived size distribution of cytosolic proteins. (A) Normalized histogram representation of the mass distribution of the cytosolic proteome of human proteins from the Uniprot database,³⁴ with 5217 proteins. A lognormal probability density function was fitted to the histogram (orange line). (B) Net charge density shows an approximately normal distribution centred at −0.065 e/nm². The dashed line corresponds to zero charge. (C) Optimized size distributions combining R₁ and R₂ data from the six reporter proteins into a single binding model. The optimized lognormal distribution (black) compared to the database-derived distribution (orange), corresponding to the fitted distribution in (A). The gray shaded area depicts the variation upon random removal of one (dark gray) or two (bright gray) relaxation pairs. The dashed gray line is the maximum entropy distribution from the family of solutions (Supporting Information 6, Figures S8, S9).

An additional high-mass contribution is the simultaneous interaction between multiple partners,⁴⁸ albeit that this possibility seems here disfavored by the low population of complexes formed by our current reporter proteins. Since the relaxation effect upon interaction with more than one partner is, nevertheless, indistinguishable from that with a single large entity, it is reasonable to include all transient complexes as a part of the same size and net-charge density distribution. To allow for such larger complexes to be included, we optimized p_B for each reporter protein while simultaneously optimizing a common mass distribution of interaction partners. For this purpose, we employed a generalized lognormal distribution with free optimization of the distribution parameters (Supporting Information 3). The fit optimizes n + 2 parameters for n pairs of relaxation rates (p_B for each reporter protein and 2 global distribution parameters), which means that at least two different data pairs are needed for a robust fit. We tested this approach to analyze transient binding of TTHA^pwt to lysozyme in vitro and used the two R₁/R₂ pairs from the 50 and 150 mg/mL lysosome samples to fit a distribution of M_w. Reassuringly, a narrow distribution centered around 15 kDa was obtained (Figure S5).

Next, the six pairs of in-cell relaxation rates were used in a global fit, where R₁ or R₂ alone are not enough to determine the distribution, as for a single relaxation rate, any distribution can be accommodated by a shift in p_B. We find that the distribution that best reproduces the relaxation data indeed resembles the one predicted from the natural intracellular environment: the distribution not only fits the sizes of the soluble proteins but also includes a high-mass tail that accounts for the larger cytosolic components (Figure 4, Table S2). The fitted relaxation rates are virtually identical to those from the fast-exchange model with a uniform partner of M^av = 143 kDa (Figure 3), with good agreement between calculated and observed R₁ values, where r² = 0.93 and rmsd = 0.26 (Figure 3). The distribution optimization from in-cell data yields a family of solutions for a given p_B (Figure S8), which, in turn, allows the maximum-entropy distribution to be deducted (Figure S9, Supporting Information 6). This is a distribution that explains the data, while still carrying minimal “a priori” information. As the relaxation data can be explained by a single average binding partner with mass M^av, a symmetric distribution centered at M^av would provide the distribution with less information. However, the obtained maximum entropy solution resembles the asymmetrical database-derived distribution (Figure 4) with the characteristic high mass tail.

Although our extended distribution analysis does not lead to higher precision, it strengthens the approach by demonstrating that the NMR data also complies with a physiologically realistic cell composition. Moreover, it validates the ansatz of fast exchange in transient encounters and provides a method for estimating the size distribution of macromolecules at work in live cells. To determine the robustness of the obtained distribution, we randomly removed first one and then two data pairs and repeated the fit. The test shows, reassuringly, that the distribution only exhibits small changes (Figure 4). As an additional control, we examined if the obtained distribution still reflects the intrinsic physical coupling between translational and transverse relaxation. In other words, can we accommodate any set of “inconsistent” R₁/R₂ pairs with a distribution, simply by rendering our conclusions about transient encounters nonconclusive? To test this, we prepared a set of relaxation pairs with R₁ values systematically offset to lower values, while keeping R₂ unchanged. The results show that we cannot obtain any distribution that reproduces these relaxation pairs with the same precision as the real data (Supporting Information 7, Figure S10).

Bound Population as Quantification of Transient Interactions in the Cell

Thus, use of the full distribution as possible binding partners explains both relaxation parameters using a single physically relevant model: the assumption of fast exchange between a bound and a free state (eq 1). Additionally, it provides an intuitively apprehensible parameter in the form of the population of bound protein species (p_B). The latter is here the sole specific parameter for the reporter protein and constitutes a direct measure of the actual interactivity of the protein inside the studied cell type. Upon comparing the obtained p_B values with the apparent viscosity (determined from R₂ alone), there is a common relationship with surface charge: less negative net charge results in both higher η^app and p_B. This relationship is further underlined by the clear response on surface charge mutations (Figure 5, Table S2). Notably, the response on the surface-charge perturbations seems similar for all three reporter proteins, where p_B approximately doubles with a net-charge change by two units. The reporter proteins, however, follow distinct trajectories in the net charge-p_B plane (Figure 5), probably reporting on the differences in general inter-reactivity. At the same net charge, SOD1^barrel stands out as the most interactive of the reporter proteins, while HAH1^pwt tumbles most freely (Figure 5). This result is in contrast to the more rudimentary η^app analysis, where SOD1^barrel emerges as less retarded (Figure 2). The reason for this underestimate of SOD1^barrel interactivity in the η^app analysis is that the relative change in the apparent size upon transient interactions is less for a larger protein than for a smaller one,¹⁰ while the p_B analysis takes this explicitly into account. These results serve as a good example of the advantage of using p_B determined from both longitudinal and transverse relaxation when characterizing transient interactions in live cells. Since the other readout from the global analysis is the effective size distribution, this method can also be used to observe cell-type differences and perturbations of the macromolecular size distribution in the cytosol. Accordingly, the approach can relatively simply provide new insights into cell function, cellular composition, and the formation of higher-order interactomes in live cells.

Figure 5.

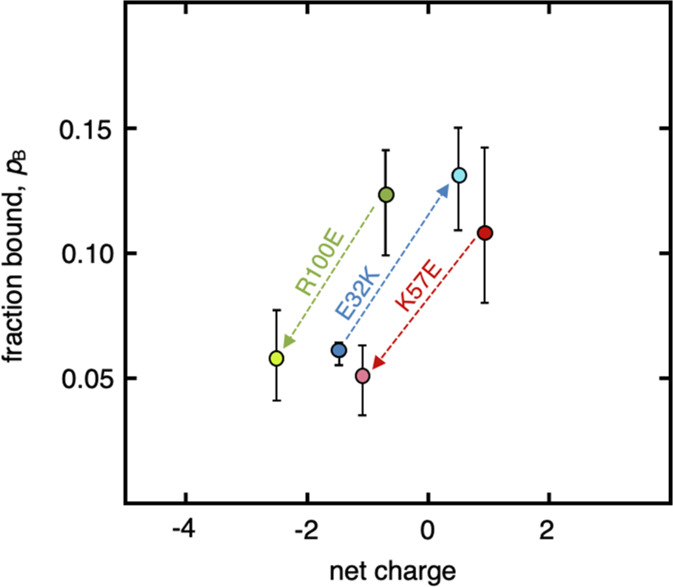
Determined bound population as a function of net charge. The optimized population from a model with transient interaction of the reporter proteins with a distribution of interaction partners, blue marker: TTHA^pwt; red marker: HAH1^pwt; and green marker: SOD1^barrel. The brighter markers correspond to the surface mutation variants of the reporter proteins and highlight the importance of surface net charge on in-cell transient encounter formations.

Concluding Remarks

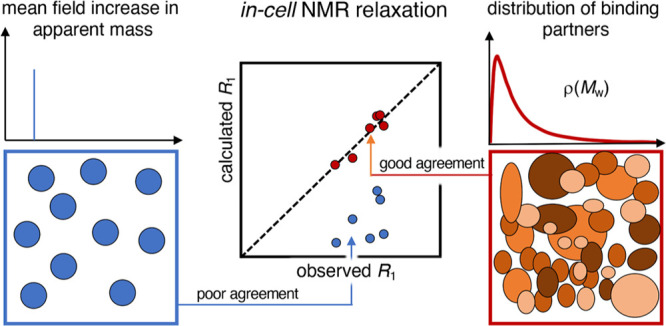
To summarize, our study shows that the mean-field approaches based on apparent viscosity fail to accurately describe the in-cell effect on NMR relaxation data since they do not explicitly account for fast exchange between the monomer and monomer–partner complexes that is bound to accompany transient-binding events (Figure 6). Taking this fast exchange into account not only reconciles the previous issue of seemingly inconsistent relaxation parameters, but also sheds light on the intracellular interactions through pinpointing the population of bound species (p_B). Of particular interest, the results show that the disparate effect of transient in-cell interactions on T₁ and T₂ can be explained by mass-altering binding alone without introducing chemical-exchange contributions (Figure 6). Although this simplifying result by no means rules out contributions from chemical-exchange effects, it is notable that they are not required to explain the observed data.

Figure 6.

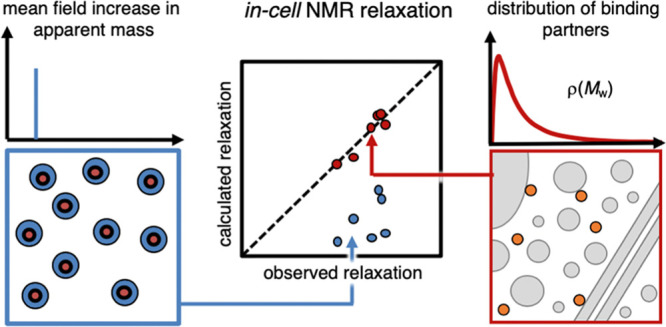
Comparing the models. The mean field approach, where a reporter protein (orange) is assigned an apparent mass (blue panel), cannot simultaneously describe in-cell R₁ and R₂ data. However, a model with the reporter protein in a single free state and a population in a distribution of bound states fully reconciles the R₁ and R₂ data. The distribution of monomeric cytosolic proteins is not sufficient by itself but transient interactions with larger components, such as protein assemblies, membranes, ribosomes, and cytoskeleton have to be accounted for.

Another interesting detail is that to accurately reproduce the observed relaxation rates, larger interaction partners than the soluble cytosolic proteins need to be included (Figure 6). This observation complies with the view that both soluble proteins and higher-order complexes, like for example, ribosomes and cytoskeletons, play important roles in modulating the rotational diffusion in live cells.^{5,12,28,46,47,49} The influence of the full distribution of intracellular interaction partners on the rotational diffusion suggests also that the NMR relaxation analysis can be used for exploring more intricate aspects of cellular function. One such example is how the interplay between the intracellular components responds to physiological or genetic perturbations, where the interaction-size distributions for some key players are expected to undergo significant changes. Although it remains to establish how far this type of analysis can be taken given the signal-to-noise and many degrees of freedom, the results in this study show that, in principle, it is doable.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c08274.

• Closed-form expression for the mass dependence of the relaxation rates, determination of η^app, the binding models, validation of the models from lysozyme binding, surface net charge estimations, maximum entropy calculations, and validation of R₁/R₂ self-consistency; materials and methods; in-cell transverse and longitudinal relaxation; protein leakage quantification; correlation between leakage and deviation from single exponentiality; apparent viscosity reference curves for longitudinal and transverse relaxation; benchmarking the method using weak interaction between TTHA^pwt and human lysozyme; comparison of the cytosolic proteome size-distributions; histogram of surface charge density for proteins of three different size ranges; family of solutions for possible size distributions of the cytosolic interactome; selected representatives for the cytosolic interactome; relaxation rate parameters need to be globally consistent to give reasonable results; longitudinal and transverse relaxation rates; and collected results for the calculations of both relaxation rates (PDF)

The authors declare no competing financial interest.