PheValuator: Development and Evaluation of a Phenotype Algorithm Evaluator.

Abstract

Background:

The primary approach for defining disease in observational healthcare databases is to construct phenotype algorithms (PAs), rule-based heuristics predicated on the presence, absence, and temporal logic of clinical observations. However, a complete evaluation of PAs, i.e., determining sensitivity, specificity, and positive predictive value (PPV), is rarely performed. In this study, we propose a tool (PheValuator) to efficiently estimate a complete PA evaluation.

Methods:

We used 4 administrative claims datasets: OptumInsight’s de-identified Clinformatics™ Datamart (Eden Prairie,MN); IBM MarketScan Multi-State Medicaid); IBM MarketScan Medicare Supplemental Beneficiaries; and IBM MarketScan Commercial Claims and Encounters from 2000-2017. Using PheValuator involves 1) creating a diagnostic predictive model for the phenotype, 2) applying the model to a large set of randomly selected subjects, and 3) comparing each subject’s predicted probability for the phenotype to inclusion/exclusion in PAs. We used the predictions as a ‘probabilistic gold standard’ measure to classify positive/negative cases. We examined 4 phenotypes: myocardial infarction, cerebral infarction, chronic kidney disease, and atrial fibrillation. We examined several PAs for each phenotype including 1-time (1X) occurrence of the diagnosis code in the subject’s record and 1-time occurrence of the diagnosis in an inpatient setting with the diagnosis code as the primary reason for admission (1X-IP-1stPos).

Results:

Across phenotypes, the 1X PA showed the highest sensitivity/lowest PPV among all PAs. 1X-IP-1stPos yielded the highest PPV/lowest sensitivity. Specificity was very high across algorithms. We found similar results between algorithms across datasets.

Conclusion:

PheValuator appears to show promise as a tool to estimate PA performance characteristics.

1.0. Introduction

In observational research, rule-based phenotype algorithms (PAs) are one way to identify subjects in a dataset who may have a particular health outcome. Empirical evidence for the validation of these PAs has traditionally been performed using clinical adjudication of a patient’s health record for a small subset of the subjects. In most cases the validation results provide an estimate of the positive predictive value (PPV) for the PA but rarely estimate the remaining elements of the validation, namely sensitivity and specificity.^1-4 The reason is often due to the time, expense, and practicality of examining a large set of records from both those with the phenotype and those without. This incomplete validation does not provide researchers with all the necessary information to ensure that they are using the correct approach to finding the correct subjects for their studies. In this study, we propose a method to estimate all the parameters of a PA validation using diagnostic predictive modeling.

Systematic reviews of PA validation studies provide examples of incomplete validation. Rubbo and colleagues performed a systematic review of PA validation for acute myocardial infarction (AMI).¹ In their analysis of 33 validation studies, they found that, while all studies provided estimates of PPV, only 11 also provided estimates for sensitivity and 5 provided estimates for specificity. McCormick et al. examined 21 validation studies for acute stroke PAs where 15 determined sensitivity and 3 determined specificity.² A systematic review of PAs for atrial fibrillation (AF) found, that out of 10 studies examined, 4 studies provided estimates for sensitivity and 2 for specificity.⁵ While PPV is a useful measure, it is dependent on the prevalence of the phenotype in the sampled population.⁶ Unless the data used in one’s research has the same phenotype prevalence, the PPV from the validation study may not be applicable. In addition to the lack of key measures of PA performance (e.g., sensitivity and specificity), Widdifield and colleagues found significant methodological differences in validation efforts for rheumatic diseases.⁴ For example, in the 23 studies included in their analysis, about two thirds used diagnostic codes to determine cases and validated on medical records. The other one third of the studies used the reverse method. They emphasize how these differences may affect the validation results. Incomplete validation results and results from varying methodologies may significantly affect the use of PAs within observational research.

In addition to the high cost for PA validation using traditional methods, another challenge with reliance on source record validation is the assumption that results from validation studies is applicable to the data for the study of interest, whether that be a different dataset or a different time period with the same dataset. Terris et al. presented rationale for potential sources of heterogeneity between databases based on differences on the quality and quantity of data collected prior to entry within the database.⁷ They suggested that these possible sources of bias be included in any presentation of results using secondary data. Madigan et al. found significant heterogeneity in their results from comparative cohort studies.⁸ Their results also suggest that databases may have specific data collection methodologies and different performance characteristics for phenotypes. Understanding the performance characteristics of PAs within specific databases used in research is critical to understanding potential sources of possible bias-driven differences between studies using observational data.

In addition to the time and expense of performing clinical adjudication on medical records associated with observational data, obtaining permission to view the detailed records is difficult and may produce results that are subject to selection bias. Kho and colleagues examined 17 studies where consent was obtained to view detailed medical records.⁹ They found significant differences between the patients whose records were obtained and those whose records were not.

The objective of this research was to develop a method for validating PAs for any phenotype without the need for clinical adjudication of patient records. This method would allow researchers to estimate the full performance characteristics (sensitivity, specificity, positive predictive value, and negative predictive value) for any algorithm in any dataset.

2.0. Methods

Data for this study were collected from 5 datasets: IBM^® MarketScan^® Commercial Claims and Encounters Database, ages 18-62 years (CCAE); IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database, ages 66 years and greater (MDCR); IBM^® MarketScan^® Multi-State Medicaid, ages 18-62 years (MDCD); Optum© De-Identified Clinformatics^® Data Mart Database – Date of Death (OptumInsight, Eden Prairie,MN); and Optum© de-identified Electronic Health Record Dataset (PanTher). CCAE and MDCD were limited to patients aged 18-62, while MDCR was restricted to patients greater than 66. Optum and PanTher were stratified by ages 18-62 years (Optum1862, PanTher 1862) and ages 66 years and greater (OptumGE66, PanTher66);Data were from subject records starting January 1, 2010 until June 30, 2018 with the exception of MDCD, which included data until December 31, 2016. Each database was transformed to the OMOP common data model (CDM). The full specification for each extract, transform, and load (ETL) procedure for each of the databases used in this study is publicly available at: https://github.com/OHDSI/ETL-CDMBuilder. The OMOP CDM is an open community standard that normalizes the structure (e.g. tables, fields, datatypes) and content (e.g. vocabularies used across each clinical domain) for managing observational data, and is accompanied by community conventions for best practices of how to ETL from source data into the CDM. The OMOP CDM is a person-centric model that accommodates timestamped clinical observations from an array of clinical domains, including conditions, drugs, procedures, devices and measurements. For any ETL, source vocabulary codes require mapping to the OMOP standardized vocabularies (which are predominantly based on international standards such as SNOMED-CT, RxNorm, and LOINC); for all of these sources, the mappings used in the ETL were provided by the OHDSI community (as available at athena.ohdsi.org). Source data are routed to the appropriate clinical domain within the OMOP structure and augmented with the OMOP standard concepts. The Optum and IBM^® MarketScan^® databases used in this study were reviewed by the New England Institutional Review Board (IRB) and were determined to be exempt from broad IRB approval, as this research project did not involve human subject research.

The process was as follows:

1. Develop a diagnostic predictive model for a phenotype: Diagnostic predictive models are used to estimate the probability that a specific outcome or disease is present in an individual.¹⁰ The output of the model is a set of weighted predictors for diagnosing a phenotype.

2. Determine the probability of a phenotype for each individual in a large group of subjects: The set of predictors from the model can be used to estimate the probability of the presence of a phenotype in an individual. We use these predictions as a ‘probabilistic gold standard’.

3. Evaluating the performance characteristics of the PAs: We compare the predicted probability to the binary classification of a PA (the test conditions for the confusion matrix). Using the test conditions and the estimates for the true conditions, we can fully populate the confusion matrix and determine the full set of performance characteristics, i.e., sensitivity, specific, and predictive values.

PheValuator was programmed in R, and can be applied to any OMOP CDM v5-compliant database. The full documentation and source code to implement PheValuator is available at: github.com/ohdsi/phevaluator.

Process Steps:

1). Develop a diagnostic predictive model for a phenotype:

A predictive model is developed using a set of labeled data where the label represents the presence or absence of the phenotype for each subject in the dataset. For the subjects labeled as having the phenotype, we used an extremely specific (“xSpec”) PA, ensuring that these subjects would have the phenotype with a very high likelihood. For the subjects to be labeled as not having the phenotype, we excluded any subjects with the diagnosis codes used to create the extremely specific PA for the phenotype, ensuring that these subjects would not have the phenotype with a high likelihood.

For this study, we tested our methods on four phenotypes, chronic kidney disease (CKD), atrial fibrillation (AF), acute myocardial infarction (AMI), and cerebral infarction.

1a). Creating the extremely specific (“xSpec”), sensitive, and prevalence cohorts:

xSpec Cohort: The first step in the process was to find subjects with a very high likelihood of having the phenotype. These subjects are used as ‘noisy labeled’ positives to be used in the predictive model. To achieve high specificity for the phenotype, we used a technique from a prior study which chose subjects with multiple occurrences of the phenotype in their medical record.¹¹ For example, for the AMI xSpec cohort, we used a PA requiring five or more occurrences of a diagnosis of MI in a subject’s record with at least two occurrences being a diagnosis from an in-patient setting. For this PA we used diagnosis codes for specific sub-types of the phenotype. For example, for AMI we included the Systematized Nomenclature of Medicine (SNOMED) diagnosis code, “acute subendocardial infarction”, “acute non-ST segment elevation myocardial infarction”, and “acute ST segment elevation myocardial infarction” along with several other sub-types of AMI. We did not include the SNOMED ancestor diagnosis code, “Acute myocardial infarction”.

Sensitive Cohort: We also developed a sensitive PA used to find a large proportion of the subjects in the database who may have the phenotype, so that they can be excluded when creating the ‘noisy negative’ labels. The PA to identify these subjects was a simple algorithm requiring 1 or more of the condition codes used to create the xSpec PA for the phenotype in the subject record.

Prevalence Cohort: The third PA we developed was for creating a cohort to allow us to determine the prevalence of the phenotype in the dataset. As an example, for AMI, the PA included all subjects with at least one diagnostic code for AMI or any of the sub-types of AMI. For AMI, we used the SNOMED diagnosis code, “acute myocardial infarction” and all the SNOMED descendants, e.g., “acute subendocardial infarction”.

1b). Creating the Target and Outcome Cohorts:

The next step was to create the target and outcome cohorts to be used as a dataset of subjects for the diagnostic prediction model as per the recommendations of Reps et al.¹² The target cohort contains all subjects, both positive and negative for the phenotype, to be used in the model. The outcome cohort is used to label the subjects in the target cohort as positive for the phenotype. The process flow for this step was as follows:

1. Estimate the population prevalence of the phenotype in each database using the prevalence cohort. This was done in order to correctly determine the relative proportion of those positive and negative for the phenotype in the modeling dataset ensuring a well-calibrated model.

2. Construct the target population of subjects for the diagnostic predictive model.

   1. ‘Positive labels’ for the phenotype: for the ‘positive labels’ to be used in the modeling process, we used subjects included in the xSpec cohort.
   2. ‘Negative labels’ for the phenotype: we select a random set of subjects from the overall dataset excluding those in the sensitive cohort.
   3. Balance the number of ‘positive labels’ and ‘negative labels’ to approximate the prevalence of the phenotype: Using the estimated population prevalence, we sample a defined number of ‘positive labels’ and a proportionate number of ‘negative labels’ to make the ratio the same as the prevalence. For example, if the prevalence was 10%, we included 1500 ‘positive labels’ and 9 X 1500 ‘negative labels’ for a total population of 15000.

3. Use the xSpec cohort as the outcome cohort to label the xSpec subjects in the constructed target population as “positive labels”, i.e., positive for the phenotype, and label the remaining subjects “negative labels”.

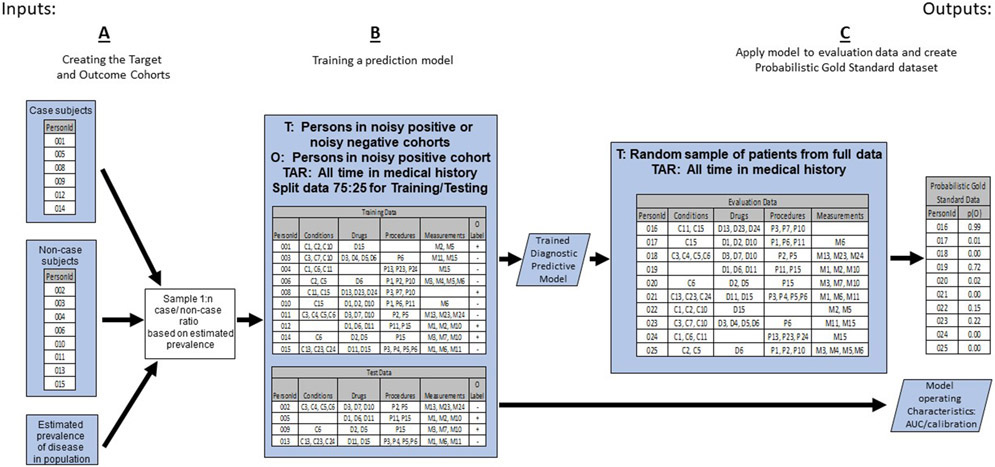
These steps are depicted in “A” of Figure 1.

Figure 1:

The First Portion of the PheValuator Process Flow Creating the Target and Outcome Cohorts to be used in Training the Diagnostic Predictive Model for Developing the Probabilistic Gold Standard Phenotype Data set to be used in Phenotype Algorithm Evaluation.

T – Target Cohort; O – Outcome Cohort; TAR – Time-At-Risk;

1c). Creating a Diagnostic Prediction Model:

We used the Patient Level Prediction (PLP) R package to create a diagnostic prediction model for the phenotype.¹² To inform the model, we extracted data from all time in each subject’s health record including conditions, drugs, procedures, clinical observations, and occurrences of measurements. We used all available data in each data set for development of the prediction model. The covariates used were: age as a continuous variable; sex; presence/absence of in-patient or out-patient diagnosed condition classes based on the Systematized Nomenclature of Medicine-Clinical Terms (SNOMED-CT) hierarchy of conditions; presence/absence of drug exposures based on filled drug prescriptions and using the RxNorm naming system for generic and branded drugs; presence/absence of a clinical procedure based on the Current Procedural Terminology, 4th Edition (CPT-4); and the presence/absence of laboratory measurements. The machine learning algorithm used in this study was logistic regression with Least Absolute Shrinkage and Selection Operator (LASSO) L1-regularization.¹³ For model development, similar to the method used by Agarwal et al., we excluded all diagnosis codes used in the creation of the xSpec model.¹⁴ Thus, none of the codes used to create the positives (i.e., the codes used in the xSpec PA) or negatives in the population to be modeled would be included in the final model used to determine the probability of having the phenotype. The purpose for excluding these codes was to prevent circularity when testing the PAs to be used in research studies. The model was developed on a random selection of 75% of the target cohort, the “train” subjects, and internally validated on the remaining 25% of the subjects, the “test” subjects. The PatientLevelPrediction package performs stratified sampling to ensure the proportion of outcomes in the training (75%) set is equal to the proportion of outcomes in the test (25%) set. Each machine learning algorithm within the PatientLevelPrediction package performs its own cross-validation within the “train” dataset for hyperparameter tuning. The implementation of LASSO logistic regression performs k-fold cross-validation within a grid-search to identify an optimal regularization hyperparameter.¹⁵ Once a model is developed on “train” set, internal validation is conducted by applying the model developed from the train data on the test data and determining the model’s performance characteristics including discrimination, as measured by Area Under ROC curve, and calibration. The models developed were used if they showed excellent performance characteristics on internal validation, i.e., an area under the receiver operator characteristics curve (AUC) of greater than 0.95. The output of this step was a model comprising a set of weighted predictors that were used to determine the probability of the presence or absence of the phenotype in subjects.

This step is depicted in “B” of Figure 1.

2). Determining the probability of a phenotype for each individual in a large group of subjects:

The next step was to develop a cohort of subjects to use for evaluating the performance characteristics of the PAs, the “evaluation cohort”. In traditional PA validation, the PA is compared against a group of subjects whose presence or absence of the phenotype is determined by clinical adjudication using the complete set of patient records. As this is not possible with large administrative datasets, we replaced clinical adjudication with the probability of the presence or absence of the phenotype as determined by the predictive model. First, we selected a large, random subset of subjects from the database. For our very large databases, we selected about 2,000,000 subjects for the evaluation cohort. We extracted covariates from this population from their entire health record based the predictors from the model developed in the previous step. We used the applyModel function of PLP on the evaluation cohort to determine the probability of the presence of the phenotype. The output of this step was a large cohort of subjects each with a predicted probability for the phenotype.

This step is depicted in “C” of Figure 1.

3). Evaluating the Performance Characteristics of the PAs

Developing PAs for Testing:

We used a variety of PAs for testing. Many PAs for cohort development use variations of the phenotype condition codes with either high sensitivity or high specificity depending on the purpose of the cohort. Four commonly used PAs that we included in our testing were:

1. 1 or more occurrences of the diagnosis code for the phenotype (“≥1 X Dx Code”). The diagnostic codes used in this PA, as well as in 2, 3, and 4 below, were the same codes used in the PA for prevalence cohort.

2. 2 or more occurrences of the diagnosis code for the phenotype (“≥ 2 X Dx Code”)

3. 1 or more occurrences of the diagnosis code for the phenotype from a hospital in-patient setting (“≥1 X Dx Code, In-Patient”)

4. 1 or more occurrences of the diagnosis code for the phenotype from a hospital in-patient setting and determined to be the primary reason for hospital admission (“≥1 X Dx Code, In-Patient, 1st Position”)

We also developed several other PAs that included clinical procedures or laboratory measurements for the treatment of the phenotype along with diagnosis codes for the phenotype. As an example, for AF we developed a PA where subjects were selected based on having a procedure for cardioversion or atrial ablation along with a diagnosis code for AF. These PAs were developed to select a group of subjects with a very high likelihood of having the phenotype, i.e., minimal misclassification, as the performance of a clinical procedure would likely eliminate the presence of a diagnosis code as a “rule out” diagnosis or entered in the subject record in error.

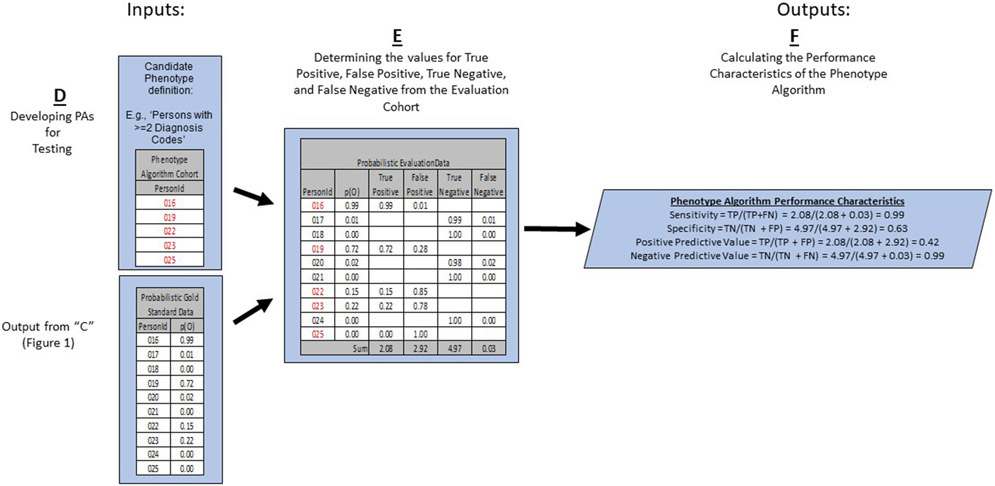
This step is depicted in “D” of Figure 2.

Figure 2:

The Last Portion of the PheValuator Process Flow Using Test Phenotype Algorithms along with the Probabilistic Gold Standard Phenotype Data for Developing the Performance Characteristics of the Phenotype Algorithm.

p(O) – Probability of Outcome; TP – True Positive; FN – False Negative; TN – True Negative; FP – False Positive

Determining the values for True Positive, False Positive, True Negative, and False Negative from the Evaluation Cohort:

In this process, we used the probability of the phenotype determined by the diagnostic predictive model in place of a binary designation as a ‘probabilistic gold standard’. For example, the likelihood that, say, subject #1 has the phenotype would be higher if subject #1 had many diagnoses, clinical procedures, drug exposures, and laboratory measurements indicative of the phenotype (and thus possibly included in the predictive model) compared to, say, subject #2 with only diagnosis codes for the phenotype in his/her health record. In the case of subject #1, the procedure codes, for example, may bring greater assurance that the subject actually had the phenotype rather than simply had a diagnosis code as a “rule out” diagnosis, which may be more likely in subject #2. This may be seen as analogous to the process in traditional PA validations where the adjudication of, say, three clinicians are used while employing the technique of “majority rules”. For a subject where three out of three clinicians deem a subject a case based on the information included the subject’s record and the subject is thereby designated a case, our method should deem this subject as having the phenotype with a probability near one. The advantage of our method becomes apparent in less clear situations. For example, when two out of the three clinicians agree that the subject is a case and one clinician disagrees, the designation for this subject would be as a case based on “majority rules” and, although one clinician did not consider the subject a case, he/she is treated as equivalent to the subject where all three clinicians agreed. Our approach provides the flexibility to designate this subject as having a 67% probability of being a case. Our method incorporates the inherent uncertainty that is present in a subject’s health record.

We continue our example from above to illustrate the use of probabilities for the confusion matrix (Figure 2E). We examined the cohort formed from the PA and found those subjects from the evaluation cohort created in the previous step who were included in the PA cohort (PersonIds 016, 019, 022, 023, and 025) and those from the evaluation cohort who were not included (PersonIds 017, 018, 020, 021, and 024). For each of these included/excluded subjects, we had previously determined the probability of the phenotype using the predictive model.

We approximated the values for True Positives, True Negatives, False Positives, and False Negatives as follows:

1. If the PA included a subject from the evaluation cohort, i.e., the PA considered the subject a “positive”, the predicted probability for the phenotype was added to the True Positives value and one minus the predicted probability for the phenotype was added to the False Positives value. For example, PersonId 016 (Figure 2E) had a predicted probability of 99% for the presence of the phenotype, 0.99 was added to the True Positives (“99% correct”) and 1.00 - 0.99 = 0.01 was added to the False Positives (“1% incorrect”). This was repeated for all the subjects from the evaluation cohort included in the PA cohort (i.e., PersonIds 019, 022, 023, and 025).

2. If the PA did not include a subject from the evaluation cohort, i.e., the PA considered the subject a “negative”, one minus the predicted probability for the phenotype for that subject was added to the True Negatives value and the predicted probability for the phenotype was added to the False Negatives value. For example, PersonId 017 had a predicted probability of 1% for the presence of the phenotype (and, correspondingly, 99% for the absence of the phenotype) and 1.00 – 0.01 = 0.99 was added to the True Negatives (“99% correct”) and 0.01 was added to the False Negatives (“1% incorrect”). This was repeated for all the subjects from the evaluation cohort not included in the PA cohort (i.e., PersonIds 018, 020, 021, and 024).

After summing these values over the full set of subjects in the evaluation cohort, we filled the four cells of the confusion matrix and were able to estimate the PA performance characteristics.

Calculating the Performance Characteristics of the Phenotype Algorithm:

The performance characteristics we calculated were:

1. Sensitivity defined as True Positives/(True Positives + False Negatives)

2. Specificity defined as True Negatives /(True Negatives + False Positives)

3. Positive Predictive Value defined as True Positives/(True Positives + False Positives)

4. Negatives Predictive Value defined as True Negatives /(True Negatives + False Negatives)

In the example in Figure 2F, the sensitivity, specificity, PPV, and NPV were 0.99, 0.63, 0.42, and 0.99, respectively.

We calculated the performance characteristics for each PA for the four phenotypes. All cohort definitions were created using the OHDSI ATLAS tool. JSON files for all the PAs used in this research are available upon request.

3.0. Results

The performance characteristics of the diagnostic predictive models used in this study for the four phenotypes are shown in Table 1. Each model showed excellent performance characteristics with areas under the Receiver Operator Characteristics curve at 0.98 and above for all phenotypes in each of the databases tested. This indicates that the models were able to effectively discriminate between the positive and negative labels. The calibration curves also showed excellent performance with intercepts at 0 and slopes close to unity, the ideal value. This indicates that the models were able to accurately predict outcomes across the full range of predicted probabilities. We found that the average predicted probability for cases in the test dataset ranged from an average of about 77% for AMI to 88% for cerebral infarction. The average predicted probability for non-cases was 2% or less for all phenotypes across the 4 databases tested.

Table 1:

Performance Characteristics of the Diagnostic Predictive Models used to Create Probabilistic Gold Standard Datasets

Phenotype	Database	AUC	Calibration Intercept	Calibration Slope	Average Predicted Probability Case	Median Predicted Probability Case	Average Predicted Probability Non-Case	Median Predicted Probability Non-Case
Chronic Kidney Disease	CCAE	0.997	0	1.00	0.87	1.00	0.00	0.00
	Optum1862	0.996	0	1.05	0.84	1.00	0.00	0.00
	OptumGE66	0.977	0	1.02	0.79	0.97	0.04	0.01
	MDCD	0.997	0	1.02	0.88	1.00	0.00	0.00
	MDCR	0.988	0	1.01	0.85	1.00	0.03	0.00
	PanTher1862	0.993	0	1.02	0.81	0.98	0.01	0.00
	PanTherGE66	0.982	0	1.01	0.78	0.94	0.03	0.00
Atrial Fibrillation	CCAE	0.999	0	0.98	0.86	0.98	0.00	0.00
	Optum1862	0.999	0	0.97	0.87	0.97	0.00	0.00
	OptumGE66	0.992	0	1.00	0.84	0.94	0.02	0.00
	MDCD	0.996	0	0.98	0.78	0.91	0.00	0.00
	MDCR	0.996	0	1.01	0.88	0.99	0.02	0.00
	PanTher1862	0.998	0	1.01	0.84	0.96	0.00	0.00
	PanTherGE66	0.994	0	1.02	0.84	0.95	0.03	0.00
Myocardial Infarction	CCAE	1.000	0	1.00	0.84	0.97	0.00	0.00
	Optum1862	1.000	0	0.98	0.86	0.97	0.00	0.00
	OptumGE66	0.994	0	1.05	0.74	0.91	0.01	0.00
	MDCD	0.998	0	1.01	0.76	0.92	0.00	0.00
	MDCR	0.994	0	1.04	0.77	0.94	0.01	0.00
	PanTher1862	0.998	0	1.03	0.76	0.94	0.00	0.00
	PanTherGE66	0.984	0	1.02	0.68	0.83	0.02	0.00
Cerebral Infarction	CCAE	1.000	0	1.01	0.90	1.00	0.00	0.00
	Optum1862	1.000	0	1.02	0.90	0.99	0.00	0.00
	OptumGE66	0.999	0	1.04	0.87	0.99	0.01	0.00
	MDCD	0.999	0	0.99	0.88	1.00	0.00	0.00
	MDCR	0.998	0	1.00	0.91	1.00	0.01	0.00
	PanTher1862	0.996	0	0.99	0.82	0.99	0.00	0.00
	PanTherGE66	0.991	0	1.01	0.79	0.97	0.01	0.00

AUC – Area Under Receiver Operator Characteristics Curve; CCAE - IBM^® MarketScan^® Commercial Claims and Encounters Database, ages 18-62 years; MDCR - IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database, ages 66 years and greater; MDCD - IBM^® MarketScan^® Multi-State Medicaid, ages 18-62 years; Optum1862 - Optum© De-Identified Clinformatics^® Data Mart Database – Date of Death, ages 18-62 years; OptumGE66 - ages 66 years and greater; PanTher1862 - Optum© de-identified Electronic Health Record Dataset, ages 18-62 years; PanTherGE66 - Optum© de-identified Electronic Health Record Dataset, ages 66 years and greater

We examined how PheValuator performed using four PAs that are common in the literature. We found that as the specificity of the PAs increased by including more parameters in the algorithm (e.g., increasing the specificity of the PA from ≥1 instance of a diagnosis code for the phenotype, “>=1 X DX Code”, to ≥1 instance of a diagnosis code for the phenotype in a hospital in-patient setting with the diagnosis code being the primary reason for discharge, “1 X DX Code, In-Patient, 1st Position”), the results from PheValuator showed increases in specificity as well as decreases in sensitivity (Tables 2a and 2b). Chronic kidney disease (CKD) was one of the phenotypes we examined. We found that as the specificity of the PA increased, we saw small changes in specificity and large changes in sensitivity. The average specificity in the seven datasets tested increased from about 95.2% to 99.9%. The average sensitivity decreased from about 81.9% to about 11.0%. Along with sensitivity and specificity we saw increases in PPV as the specificity of the PA increased. For CKD, the average PPV for the >= 1X PA was about 52.8% and increased to 87.8% for the >=1X, IP, 1^st Pos. PA. Similar patterns of change were found in the other phenotypes tested.

Table 2a:

Performance Characteristics of Four Phenotype Algorithms using Diagnostic Condition Codes to Determine Chronic Kidney Disease and Atrial Fibrillation on Multiple Datasets using PheValuator. The continuous 3-color heat map for the data in the table was defined as Red (value = 0), Yellow (value = 0.5), and Green (value = 1).

		Chronic Kidney Disease					Atrial Fibrillation
Phenotype Algorithm	Database	Sens	PPV	Spec	NPV		Sens	PPV	Spec	NPV
>=1 X HOI	CCAE	0.798	0.445	0.990	0.998		0.924	0.281	0.990	0.999
	Optum1862	0.822	0.497	0.985	0.997		0.912	0.399	0.989	0.999
	OptumGE66	0.856	0.601	0.888	0.969		0.948	0.478	0.906	0.995
	MDCD	0.903	0.484	0.974	0.997		0.930	0.323	0.984	0.999
	MDCR	0.840	0.501	0.910	0.981		0.956	0.360	0.890	0.997
	PanTher1862	0.711	0.592	0.990	0.994		0.908	0.480	0.991	0.999
	PanTherGE66	0.806	0.575	0.929	0.976		0.930	0.459	0.912	0.994
>= 2 X HOI	CCAE	0.707	0.551	0.994	0.997		0.818	0.341	0.993	0.999
	Optum1862	0.760	0.581	0.990	0.996		0.799	0.463	0.993	0.998
	OptumGE66	0.802	0.653	0.916	0.959		0.887	0.525	0.927	0.989
	MDCD	0.841	0.578	0.983	0.996		0.783	0.386	0.990	0.998
	MDCR	0.757	0.574	0.940	0.973		0.890	0.400	0.914	0.992
	PanTher1862	0.679	0.624	0.992	0.994		0.857	0.514	0.993	0.999
	PanTherGE66	0.778	0.596	0.937	0.973		0.895	0.478	0.922	0.991
>=1 X HOI, In-Patient	CCAE	0.282	0.673	0.999	0.993		0.466	0.390	0.997	0.998
	Optum1862	0.371	0.745	0.998	0.988		0.480	0.511	0.996	0.996
	OptumGE66	0.372	0.794	0.981	0.888		0.569	0.550	0.958	0.961
	MDCD	0.579	0.670	0.992	0.989		0.631	0.419	0.993	0.997
	MDCR	0.417	0.699	0.981	0.940		0.623	0.436	0.948	0.975
	PanTher1862	0.231	0.769	0.999	0.985		0.269	0.545	0.998	0.993
	PanTherGE66	0.296	0.718	0.986	0.922		0.357	0.502	0.972	0.950
1 X HOI, In-Patient, 1st Position	CCAE	0.127	0.837	0.999	0.991		0.359	0.422	0.998	0.997
	Optum1862	0.132	0.895	0.999	0.984		0.313	0.551	0.998	0.995
	OptumGE66	0.093	0.907	0.998	0.848		0.355	0.591	0.978	0.943
	MDCD	0.252	0.861	0.999	0.980		0.444	0.513	0.997	0.996
	MDCR	0.093	0.907	0.998	0.848		0.355	0.591	0.978	0.943
	PanTher1862	0.040	0.901	0.999	0.981		0.136	0.617	0.999	0.992
	PanTherGE66	0.035	0.838	0.999	0.897		0.158	0.560	0.990	0.936

Sens – Sensitivity ; PPV – Positive Predictive Value ; Spec – Specificity; NPV – Negative Predictive Value; Dx Code – Diagnosis code for the phenotype; CCAE - IBM^® MarketScan^® Commercial Claims and Encounters Database, ages 18-62 years; MDCR - IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database, ages 66 years and greater; MDCD - IBM^® MarketScan^® Multi-State Medicaid, ages 18-62 years; Optum1862 - Optum© De-Identified Clinformatics^® Data Mart Database – Date of Death, ages 18-62 years; OptumGE66 - ages 66 years and greater; PanTher1862 - Optum© de-identified Electronic Health Record Dataset, ages 18-62 years; PanTherGE66 - Optum© de-identified Electronic Health Record Dataset, ages 66 years and greater

Table 2b:

Performance Characteristics of Four Phenotype Algorithms using Diagnostic Condition Codes to Determine Myocardial Infarction and Cerebral Infarction on Multiple Datasets using PheValuator. The continuous 3-color heat map for the data in the table was defined as Red (value = 0), Yellow (value = 0.5), and Green (value = 1).

		Acute Myocardial Infarction					Cerebral Infarction
Phenotype Algorithm	Database	Sens	PPV	Spec	NPV		Sens	PPV	Spec	NPV
>=1 X HOI	CCAE	0.761	0.598	0.997	0.999		0.811	0.268	0.994	0.999
	Optum1862	0.723	0.530	0.995	0.998		0.808	0.227	0.990	0.999
	OptumGE66	0.643	0.534	0.973	0.982		0.837	0.252	0.938	0.996
	MDCD	0.676	0.468	0.990	0.996		0.836	0.299	0.980	0.998
	MDCR	0.665	0.553	0.977	0.985		0.797	0.317	0.950	0.994
	PanTher1862	0.630	0.479	0.994	0.997		0.741	0.479	0.994	0.998
	PanTherGE66	0.574	0.431	0.971	0.984		0.739	0.419	0.966	0.991
>= 2 X HOI	CCAE	0.585	0.769	0.999	0.998		0.649	0.425	0.998	0.999
	Optum1862	0.495	0.693	0.998	0.996		0.647	0.335	0.995	0.999
	OptumGE66	0.382	0.644	0.990	0.971		0.665	0.340	0.968	0.991
	MDCD	0.454	0.628	0.996	0.993		0.697	0.421	0.990	0.997
	MDCR	0.418	0.674	0.991	0.975		0.632	0.436	0.976	0.989
	PanTher1862	0.519	0.582	0.997	0.996		0.604	0.590	0.997	0.997
	PanTherGE66	0.447	0.501	0.983	0.979		0.619	0.500	0.980	0.987
>=1 X HOI, In-Patient	CCAE	0.674	0.737	0.999	0.998		0.670	0.486	0.998	0.999
	Optum1862	0.623	0.693	0.998	0.997		0.628	0.439	0.997	0.999
	OptumGE66	0.521	0.655	0.987	0.977		0.649	0.446	0.980	0.991
	MDCD	0.573	0.593	0.995	0.994		0.632	0.494	0.993	0.996
	MDCR	0.544	0.649	0.987	0.980		0.624	0.501	0.982	0.989
	PanTher1862	0.267	0.641	0.999	0.993		0.255	0.634	0.999	0.995
	PanTherGE66	0.265	0.541	0.991	0.972		0.302	0.562	0.992	0.977
1 X HOI, In-Patient, 1st Position	CCAE	0.633	0.788	0.999	0.998		0.633	0.529	0.998	0.999
	Optum1862	0.581	0.754	0.999	0.997		0.588	0.479	0.998	0.998
	OptumGE66	0.445	0.711	0.991	0.974		0.604	0.492	0.984	0.990
	MDCD	0.499	0.666	0.997	0.993		0.560	0.544	0.995	0.996
	MDCR	0.445	0.711	0.991	0.974		0.604	0.492	0.984	0.990
	PanTher1862	0.205	0.702	0.999	0.993		0.191	0.686	0.999	0.994
	PanTherGE66	0.185	0.592	0.995	0.970		0.228	0.604	0.995	0.975

Sens – Sensitivity ; PPV – Positive Predictive Value ; Spec – Specificity; NPV – Negative Predictive Value; Dx Code – Diagnosis code for the phenotype; CCAE - IBM^® MarketScan^® Commercial Claims and Encounters Database, ages 18-62 years; MDCR - IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database, ages 66 years and greater; MDCD - IBM^® MarketScan^® Multi-State Medicaid, ages 18-62 years; Optum1862 - Optum© De-Identified Clinformatics^® Data Mart Database – Date of Death, ages 18-62 years; OptumGE66 - ages 66 years and greater; PanTher1862 - Optum© de-identified Electronic Health Record Dataset, ages 18-62 years; PanTherGE66 - Optum© de-identified Electronic Health Record Dataset, ages 66 years and greater

We next examined the performance of PheValuator with PAs using clinical procedure codes or laboratory measurements either stand-alone or combined with diagnosis codes. For CKD, we tested the use of renal dialysis, a procedure specific for CKD, as a PA. As expected, the sensitivity decreased dramatically to an average of about 8.6% while the specificity rose to nearly 100% (Table 3). With those changes we saw a large increase in the average PPV which increased to about 96%. We used estimated glomerular filtration rate (eGFR) as an indicator for CKD. For this PA, we predicted that sustained eGFRs <= 60 ml/min/1.73 m² would be strongly indicative of CKD as per clinical guidelines. However, we found that the PPV for 3 low eGFR measures during one year averaged about 62.5%. This low PPV was similar to that found by Kern and colleagues who concluded that diagnosis codes for CKD were specific but insensitive.¹⁶

Table 3:

Performance Characteristics of Phenotype Algorithms using Diagnosis codes plus Clinical Procedures to Determine Health Outcomes of Interest on Multiple Datasets using PheValuator. The continuous 3-color heat map for the data in the table was defined as Red (value = 0), Yellow (value = 0.5), and Green (value = 1).

Phenotype Algorithm (HOI)	Database	Sens	PPV	Spec	NPV
Dialysis Alone (CKD)	CCAE	0.094	0.954	0.999	0.991
	Optum1862	0.088	0.967	0.999	0.983
	OptumGE66	0.031	0.984	0.999	0.840
	MDCD	0.261	0.965	0.999	0.980
	MDCR	0.058	0.970	0.999	0.908
	PanTher1862	0.047	0.947	0.999	0.981
	PanTherGE66	0.023	0.930	0.999	0.896
Low Glomerular Filtration Rate (CKD)	CCAE	0.013	0.543	0.999	0.985
	Optum1862	0.050	0.705	0.999	0.976
	OptumGE66	0.024	0.547	0.997	0.868
	MDCR	0.078	0.706	0.991	0.802
Atrial Fibrillation plus Atrial Ablation/Cardioversion (AF)	CCAE	0.010	0.979	0.999	0.996
	Optum1862	0.008	0.968	0.999	0.992
	OptumGE66	0.006	0.953	0.999	0.917
	MDCD	0.003	0.924	0.999	0.992
	MDCR	0.005	0.949	0.999	0.940
	PanTher1862	0.014	0.956	0.999	0.991
	PanTherGE66	0.008	0.899	0.999	0.926
Coronary Artery Revascularization Alone (AMI)	CCAE	0.062	0.967	0.999	0.995
	Optum1862	0.073	0.944	0.999	0.993
	OptumGE66	0.037	0.916	0.999	0.955
	MDCD	0.037	0.905	0.999	0.987
	MDCR	0.026	0.915	0.999	0.959
	PanTher1862	0.017	0.771	0.999	0.991
	PanTherGE66	0.010	0.667	0.999	0.964
Cerebral Infarction plus Thrombo-endarterectomy (Cerebral Infarction)	CCAE	0.005	0.976	0.999	0.997
	Optum1862	0.004	0.930	0.999	0.996
	OptumGE66	0.003	0.894	0.999	0.976
	MDCD	0.002	0.974	0.999	0.990
	MDCR	0.002	0.900	0.999	0.972
	PanTher1862	0.002	0.942	0.999	0.993
	PanTherGE66	0.001	0.923	0.999	0.968

Sens – Sensitivity ; PPV – Positive Predictive Value ; Spec – Specificity; NPV – Negative Predictive Value; CKD – Chronic Kidney Disease; AMI – Acute Myocardial Infarction; CCAE - IBM^® MarketScan^® Commercial Claims and Encounters Database, ages 18-62 years; MDCR - IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database, ages 66 years and greater; MDCD - IBM^® MarketScan^® Multi-State Medicaid, ages 18-62 years; Optum1862 - Optum© De-Identified Clinformatics^® Data Mart Database – Date of Death, ages 18-62 years and OptumGE66 - ages 66 years and greater; PanTher1862 - Optum© de-identified Electronic Health Record Dataset, ages 18-62 years and PanTherGE66 - ages 66 years and greater

For atrial fibrillation (AF) we examined a PA using a procedure code for atrial ablation or cardioversion, which is very specific for AF, plus a diagnosis code for AF. For this PA, we found very low values for sensitivity (~1%), very high values for specificity (~99.9%), and high values for PPV (~95%). We used a more complex PA to test AMI. For AMI we developed a PA that required the presence of coronary revascularization (using the CPT4 procedure code for “Percutaneous transluminal revascularization of acute total/subtotal occlusion during acute myocardial infarction, coronary artery or coronary artery bypass graft, any combination of intracoronary stent, atherectomy and angioplasty”) in patients without evidence for concomitant procedures for insertion of a stent, coronary bypass, angioplasty, or atherectomy along with a diagnosis code for AMI during the same visit when the procedure occurred. For this highly specific PA, we again found low values for sensitivity (~4%) and high values for specificity (~99.9%) and PPV (~87%). We examined a very complex PA for cerebral infarction requiring the presence of a magnetic resonance imaging of computed tomography procedure along with a cerebral infarction diagnosis and thromboendarterectomy in the head or neck region followed by rehabilitation therapy. Using this highly specific PA we found results similar to other highly specific procedure codes with low sensitivities (<1%), high specificities (~99.9%), and high PPVs (~93%).

We examined how the results from PheValuator compared to results previously published for traditional PA validation (Table 4a).. Rubbo and colleagues performed a systematic review of PA validation studies.¹ We examined several of the studies to see how the results from their PA validation compared with PheValuator. Wahl and colleagues developed a PA for AMI using standard codes (i.e., ICD-9 410.XX) from an hospital inpatient visit with a length of stay between 3 and 180 days.¹⁷ They excluded subsequent AMI codes from their PA (i.e., ICD-9 410.X2). Their validation was limited to PPV where they found a result of 88.4% (177/200 subjects; 95%CI: 83.2, 92.5%). Using a similar PA, we found lower average PPVs across 5 datasets of 62.6% (range: 56.0-69.8). Choma et al developed a PA using similar AMI codes as Wahl without excluding subsequent AMI codes and required a length of stay greater than 2 days.¹⁸ They determined the PPV for this PA to be 92.8% (313/337 subjects; 95% CI: 89.6, 95.2). For this PA we again found lower average PPVs of 69.4% (range: 62.8-76.3). Finally we compared our results to Cutrona et al using a PA of standard AMI codes in the principal or primary position on facility claims for hospitalizations excluding subsequent AMI codes and without specifying a length of stay.¹⁹ Their results showed a PPV of 86.0% (123/143 subjects; 95% CI: 79.2%, 91.2%). Using a similar algorithm, we found an average PPV of 69.9% (range: 58.9-78.7).

Table 4a:

Performance Characteristics of 3 Phenotype Algorithms Replicating Those From Prior Publications to Determine Acute Myocardial Infarction on Multiple Datasets using PheValuator

Comparison	Database	Sens	PPV	Spec	NPV
Wahl	From Paper1	-	0.884 (95% CI: 0.832, 0.925)	-	-
	CCAE	0.343	0.698	0.999	0.996
	Optum1862	0.323	0.642	0.999	0.995
	OptumGE66	0.359	0.641	0.990	0.970
	MDCD	0.364	0.561	0.996	0.991
	MDCR	0.373	0.636	0.991	0.973
	PanTher1862	0.100	0.642	0.999	0.992
	PanTherGE66	0.129	0.560	0.996	0.968
	Mean:	0.284	0.626	0.996	0.984
Choma	From Paper2	-	0.928 (95% CI: 0.896, 0.952)	-	-
	CCAE	0.332	0.763	0.999	0.996
	Optum1862	0.303	0.716	0.999	0.995
	OptumGE66	0.310	0.701	0.994	0.967
	MDCD	0.324	0.643	0.998	0.991
	MDCR	0.321	0.686	0.994	0.971
	PanTher1862	0.074	0.720	0.999	0.992
	PanTherGE66	0.087	0.628	0.998	0.966
	Mean:	0.250	0.694	0.997	0.983
Cutrona	From Paper3	-	0.860 (95% CI: 0.792, 0.912)	-	-
	CCAE	0.610	0.787	0.999	0.998
	Optum1862	0.565	0.752	0.999	0.997
	OptumGE66	0.430	0.710	0.991	0.973
	MDCD	0.480	0.664	0.997	0.993
	MDCR	0.444	0.692	0.991	0.976
	PanTher1862	0.201	0.700	0.999	0.993
	PanTherGE66	0.180	0.589	0.995	0.969
	Mean:	0.416	0.699	0.996	0.986

¹Standard codes for acute myocardial infarction (i.e., ICD-9 410.XX) excluding subsequent AMI codes (i.e., ICD-9 410.X2) from an hospital inpatient visit with a length of stay between 3 and 180 days or death if length of stay is less than 3 days (Wahl et al ¹⁷)

²Standard codes for acute myocardial infarction from an hospital inpatient visit with a length of stay > 2 days (Choma at al ¹⁸)

³Standard codes for acute myocardial infarction in the principal or primary position on facility claims for hospitalizations excluding subsequent AMI codes (Cutrona et al ¹⁹)

Sens – Sensitivity ; PPV – Positive Predictive Value ; Spec – Specificity; NPV – Negative Predictive Value;; CCAE - IBM^® MarketScan^® Commercial Claims and Encounters Database, ages 18-62 years; MDCR - IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database, ages 66 years and greater; MDCD - IBM^® MarketScan^® Multi-State Medicaid, ages 18-62 years; Optum1862 - Optum© De-Identified Clinformatics^® Data Mart Database – Date of Death, ages 18-62 years; OptumGE66 - ages 66 years and greater; PanTher1862 - Optum© de-identified Electronic Health Record Dataset, ages 18-62 years; PanTherGE66 - Optum© de-identified Electronic Health Record Dataset, ages 66 years and greater

In addition to comparing our results to those from traditional validations of MI algorithms, we also compared our results to prior validation work on CKD and cerebral infarction (Table 4b). Nadkarni and colleagues validated two phenotype algorithms for CKD using data from electronic health record systems at three clinical sites.²⁰ In the first algorithm they used diagnosis and procedure codes plus glomerular filtration rate measurements. At one site (Mount Sinai Hospital) they found a PPV of 0.960 (95% CI: 0.940, 0.973). They found similar results at the other 2 clinical sites. Using a similar algorithm, our approach found a mean PPV of 0.811 (range: 0.692-0.873). We found similar results for NPV as was found in the traditional validation. They also validated an algorithm using diagnosis codes only. They found a lower PPV, 0.629 (95% CI: 0.578, 0.677) using this algorithm. We found a similar mean value for PPV, 0.716 (range: 0.626-0.890) across 5 datasets. Wahl et al developed and validated an algorithm for cerebral infarction.¹⁷ In their algorithm they used diagnosis codes for cerebral infarction and required a length of hospital stay of 3 days or greater. Their validation produced a PPV of 0.874 (95% CI: 0.820, 0.917). Our validation, using a similar algorithm, found a PPV of 0.599 (range: 0.566-0.635).

Table 4b:

Performance Characteristics of Phenotype Algorithms Replicating Those From Prior Publications to Determine Chronic Kidney Disease and Cerebral Infarction on Multiple Datasets using PheValuator

Comparison	Database	Sens	PPV	Spec	NPV
Nadkarni et al (CKD) Conditions, Procedures, GFR Measurements	From Paper1	-	0.960 (95% CI: 0.940, 0.973)	-	0.933 (95% CI: 0.909, 0.951)
	CCAE	0.001	0.814	0.999	0.989
	Optum1862	0.001	0.866	0.999	0.980
	OptumGE66	0.002	0.873	0.999	0.806
	MDCR	0.001	0.692	0.999	0.895
	Mean:	0.001	0.811	0.999	0.918
Nadkarni et al (CKD) Conditions	From Paper1	-	0.629 (95% CI: 0.578, 0.677)	-	0.543 (95% CI: 0.507, 0.578)
	CCAE	0.331	0.626	0.998	0.993
	Optum1862	0.310	0.700	0.997	0.986
	OptumGE66	0.402	0.890	0.988	0.873
	MDCD	0.349	0.700	0.994	0.976
	MDCR	0.376	0.666	0.978	0.931
	Mean:	0.354	0.716	0.991	0.952
Wahl et al (Stroke) Conditions, >=3 Days LOS	From Paper2	-	0.874 (95% CI: 0.820, 0.917)	-	-
	CCAE	0.253	0.607	0.999	0.997
	Optum1862	0.247	0.600	0.999	0.996
	OptumGE66	0.277	0.635	0.993	0.971
	MDCD	0.249	0.589	0.997	0.988
	MDCR	0.290	0.566	0.992	0.976
	Mean:	0.263	0.599	0.996	0.986

¹Nadkarni et al ²⁰

²Wahl et al ¹⁷

Sens – Sensitivity ; PPV – Positive Predictive Value ; Spec – Specificity; NPV – Negative Predictive Value; HOI – Health Outcome of Interest; CKD – Chronic Kidney Disease; CCAE - IBM^® MarketScan^® Commercial Claims and Encounters Database, ages 18-62 years; MDCR - IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database, ages 66 years and greater; MDCD - IBM^® MarketScan^® Multi-State Medicaid, ages 18-62 years; Optum1862 - Optum© De-Identified Clinformatics^® Data Mart Database – Date of Death, ages 18-62 years; OptumGE66 - ages 66 years and greater

To understand how changes in the xSpec PA affect the diagnostic predictive model, we examined 4 different, increasingly specific, versions of the xSpec PA for AF in the MDCR database (Table 5). The least specific algorithm we tested required 2 condition codes for AF in the subject’s health record. The most specific algorithm, and ultimately the xSpec PA we used for our cross-database testing, required 10 condition codes for AF in the subject’s health record. These xSpec PAs were examined using the common PAs we tested previously, e.g., “>=1 X Dx Code”. We found that, in general, as the xSpec PA became more specific for AF, i.e., increasing from requiring 2 to 10 AF condition codes in the subject’s health record, the sensitivity of the common PA increased, the specificity remained relatively unchanged, and the PPV decreased.

Table 5:

Comparison of Performance Characteristics of 4 Extremely Specific (xSpec) Phenotype Algorithms Used for Atrial Fibrillation Diagnostic Predictive Model Development in the IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database, ages 66 years and greater. The continuous 3-color heat map for the data in the table was defined as Red (value = 0), Yellow (value = 0.5), and Green (value = 1).

Test Phenotype Algorithm	xSpec Phenotype Algorithm	Sens	PPV	Spec	NPV
>=1 X AF	2 X AF	0.898	0.449	0.886	0.988
	3 X AF	0.921	0.430	0.883	0.991
	5 X AF	0.933	0.409	0.879	0.993
	10 X AF	0.956	0.360	0.890	0.997
>= 2 X AF	2 X AF	0.815	0.482	0.909	0.979
	3 X AF	0.844	0.467	0.907	0.984
	5 X AF	0.856	0.444	0.904	0.986
	10 X AF	0.890	0.400	0.914	0.992
>=1 X AF, In-Patient	2 X AF	0.527	0.512	0.948	0.951
	3 X AF	0.553	0.502	0.947	0.957
	5 X AF	0.558	0.475	0.945	0.960
	10 X AF	0.623	0.436	0.948	0.975
1 X AF, In-Patient, 1st Position	2 X AF	0.354	0.535	0.968	0.936
	3 X AF	0.377	0.533	0.968	0.942
	5 X AF	0.380	0.504	0.967	0.946
	10 X AF	0.447	0.472	0.968	0.965
AF + Ablation/Cardioversion	2 X AF	0.004	0.955	0.999	0.907
	3 X AF	0.005	0.963	0.999	0.913
	5 X AF	0.005	0.960	0.999	0.918
	10 X AF	0.005	0.949	0.999	0.940

Sens – Sensitivity ; PPV – Positive Predictive Value ; Spec – Specificity; NPV – Negative Predictive Value; AF – Atrial Fibrillation

4.0. Discussion

The results of this study provide support for the PheValuator tool as an alternative mechanism for estimating the performance characteristics of PAs. The results show how increasing the specificity of a PA changes the sensitivity of the algorithm. In many cases, the sensitivity may be lowered to such a great extent as to call into question whether studies using these very specific PAs are experiencing selection bias. We were able to demonstrate that the tool can evaluate PAs that are derived from data elements other than diagnostic condition codes such as procedures and clinical laboratory measures. We also found similar, albeit more conservative, estimates for PPV in our comparison between the results achieved through PheValuator and results from traditional PA validations.

We tested this method on one electronic health record (EHR) database and four insurance administrative claims databases. While the results were similar in many cases, we did observe source-specific performance differences when testing PAs that involved hospital in-patient records. This finding is likely attributable to differential capture of the phenotype in the source data, but may also be reflective of biased estimates from the ‘probabilistic gold standards’ given that each source had a differently fitted predictive model. In either case, observing different performance across sources should stimulate further exploration to assess the generalizability of the PA. In this example, since the EHR dataset is sourced by general and specialty practices and does not fully capture hospital care, a PA requiring hospital records would be expected to have lower sensitivity than a private-payer claims dataset for which most inpatient services are expected to be captured. The performance estimates from PheValuator can enable relative comparisons between data sources and PAs to understand the tradeoff in types of measurement error that may exist when applying a PA to a source for observational research.

Based on our comparisons with the 3 studies examining the PPV’s for AMI, it appears as though PheValuator may produce a more conservative estimate of the performance characteristics of PAs.^17-19 However, strict comparisons between our results and those from traditional PA validations may be prone to bias. The datasets used in our studies are likely very different than those used in prior studies. For example, the data we used to inform our models were from 2010 onward. Those in the prior studies were from data collected between 1999 to 2009. At least one major difference was that during this period US claims datasets transitioned from the use of International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9) to ICD-10. Cutrona et al. used an administrative dataset from hospital claims data which would likely have different data quality characteristics from insurance claims data. As there are likely differences in the prevalence of AMI between the datasets used in this study and those from the 3 studies compared, PPV, which is prevalence dependent, would be impacted. The small sample size used in traditional validation studies will also impact the precision of results. In our analyses we used evaluation cohorts with sample sizes of about two million subjects.

An advantage to the use of this method for PA performance measurement is that any number of PAs may be tested on each database to provide relative advantages and disadvantages of each. The use of validation results from published PAs is limited to the specific PA tested. If changes to the PA are required for study-specific reasons, the published results are no longer directly applicable. Consider, for example, if the study to be conducted required some limitation on prior therapeutic interventions, such as no prior statin use. In this case, the results from the validation studies for the PAs would likely be very different from the performance characteristics of the PAs used in the study to be conducted. Using PheValuator, this new PA for AMI with no prior statin use could be readily tested and would provide information on how the new criteria impacted, say, PA sensitivity. The tool also allows for a comparative examination of the impact of added PA elements on performance. For example, we found that including a diagnosis code from a hospital in-patient visit improved the PPV for AMI with only a small impact on sensitivity while the same PA change for AF produced only a moderate gain in PPV with a large impact on sensitivity (Table 2b).

As the models are developed using the data available within the dataset, the tool provides an estimate of PA performance based on the level of quality of the data in hand. If data is sparse within the dataset, the model will have less information to discriminate between cases and non-cases and may produce poor quality models.²¹ PheValuator provides a set of performance characteristics for the model developed which provides a level of confidence as to the validity of the results from PAs.

The importance using PA performance characteristics from a population similar to that in which the research is to be conducted may be illustrated in the CKD PA validation (Table 2a). When using the PA for “1 X Dx Code, In-Patient, 1st Position”, we found that the PPVs for the 7 datasets were quite similar with a narrow range of values between 84% and 91%. However, there was significant dissimilarity in the values for sensitivity where the values ranged from 4% to 25%. The highest sensitivity was in the MDCD population. MDCD enrollees with CKD have been shown to have poorer outcomes and have higher rates of hospitalization.²² Using performance characteristics from a PA validated on a population very different than those in MDCD would likely give disease burden estimates much higher than is actually the case. This example also underscores the need for a complete set of performance characteristics as the similarities between the PPV estimates may be misleading.

PheValuator may also be used as a way to enhance PAs. During the PheValuator process, a diagnostic prediction model is developed. The selected predictors from the model may be useful to consider as candidate criteria to include within a PA. For example, for AMI, the model included the procedure codes “Measurement of Cardiac Sampling and Pressure, Left Heart, Percutaneous Approach”, “Dilation of Coronary Artery, One Artery with Drug-eluting Intraluminal Device, Percutaneous Approach”, and “Percutaneous transluminal coronary angioplasty”. If the goal of the PA is to achieve an algorithm with a very high specificity, the investigator may want to include these procedures to locate those with AMI.

Understanding the performance characteristics of the xSpec PA used for model development is important as this algorithm ultimately determines the predicted probability of the subjects in the evaluation cohort used to test PAs used in studies. In our comparisons between increasingly specific xSpec PAs for AF in MDCR, we found that the more specific the xSpec PA is for AF, the less likely the model will infer false negatives and the more likely the model will infer false positives. This makes intuitive sense as the more specific the xSpec model the more “particular” the model will be when inferring a subject is positive based in his/her health record. In our research, we chose the most conservative PA, based on the highest PA specificity, for our testing.

Misclassification is a part of the systematic error of a study. PheValuator can be used to gain a better understanding of the level of possible misclassification by estimating the sensitivity and specificity of the PAs for the phenotype used within a study. These performance characteristics may support a researcher in the design of a study by allowing for exploration of alternative PAs with more preferable sensitivity or specificity. It can also support researchers in study execution by providing an estimate of measurement error that can be incorporated into the statistical analysis or communicated in study limitations.

CKD provides an interesting example of one of the limitations of this method: PheValuator uses predictive modeling to create a ‘probabilistic gold standard’ based on binary features extracted from the structured data available in the data, which may not reflect the desired health status for the patient. If the phenotype is undiagnosed and untreated, PheValuator will not form a model with a strong capability for detecting false negatives. In the case of CKD, clinical guidelines indicate that those with eGFR values <= 60 ml/min/1.73 m² should be considered to have CKD. Nadkarni et al found that ICD-9 codes for CKD had a PPV of about 63% based on their PA validation.²⁰ In our data, we found that the PPV for subjects with a sustained low eGFR was about 63%, i.e., PheValuator considers 37% of those with a laboratory measurement indicative of CKD to be false positive. For CKD, it is possible that instead some of these 37% false positives are in fact undiagnosed patients who are in need of treatment but not yet receiving it.

There are a number of other limitations to this method and its validation. This approach is not applicable in situations where there is only a single concept that is used to define a disease as the xSpec PA and the predictive model would both require use of that concept, which would introduce circular logic. This method relies on the use of predictive models that use all patient data for assessing probability of a phenotype. We found that errors in prediction were higher in subjects with sparse data records. This issue occurred both at the micro level (e.g., specific subjects within a database) as well as at the macro level (e.g., comparisons between databases). The development of the prediction models is also dependent on the quality of the data in the dataset, which can vary substantially.²³ The models generated within any phenotype show significant differences between datasets. As we noted, while traditional PA validation from a specific dataset may not apply to any particular observational datasets, e.g., due to prevalence differences, the results from PheValuator should be used with caution between datasets. Source record verification was not conducted as part of the validation of PheValuator in this study.

5.0. Conclusions

PheValuator represents a novel approach to phenotype evaluation by providing an automated process using a probabilistic gold standard for estimating the performance of phenotype algorithms. We believe PheValuator may be a useful tool when phenotype algorithm evaluation is required but manual chart review is infeasible or prohibitively expensive, and when multiple phenotype algorithms require comparison across a network of databases. Future work can seek to improve the predictive modeling approach within PheValuator, and to further validate the approach using additional phenotypes and data sources and comparing with source record review. Current results suggest PheValuator shows promise as a useful tool for researchers seeking to generate reliable evidence from observational data.

Abbreviations:

AF

Atrial Fibrillation

AMI

Acute Myocardial Infarction

AUC

Area Under Receiver Operator Characteristics Curve

CCAE

IBM^® MarketScan^® Commercial Claims and Encounters Database

CDM

Common Data Model

CKD

Chronic Kidney Disease

CPT-4

Current Procedural Terminology, 4th Edition

eGFR

estimated Glomerular Filtration Rate

ICD-9

International Classification of Diseases, Ninth Revision

IRB

Institutional Review Board

LASSO

Least Absolute Shrinkage and Selection Operator

MDCD

IBM^® MarketScan^® Multi-State Medicaid

MDCR

IBM^® MarketScan^® Medicare Supplemental and Coordination of Benefits Database

NPV

Negative Predictive Value

PA

Phenotype Algorithm

PLP

Patient Level Prediction

PPV

Positive Predictive Value

SNOMED

Systematized Nomenclature of Medicine