Belief dynamics extraction

Abstract

Animal behavior is not driven simply by its current observations, but is strongly influenced by internal states. Estimating the structure of these internal states is crucial for understanding the neural basis of behavior. In principle, internal states can be estimated by inverting behavior models, as in inverse model-based Reinforcement Learning. However, this requires careful parameterization and risks model-mismatch to the animal. Here we take a data-driven approach to infer latent states directly from observations of behavior, using a partially observable switching semi-Markov process. This process has two elements critical for capturing animal behavior: it captures non-exponential distribution of times between observations, and transitions between latent states depend on the animal’s actions, features that require more complex non-markovian models to represent. To demonstrate the utility of our approach, we apply it to the observations of a simulated optimal agent performing a foraging task, and find that latent dynamics extracted by the model has correspondences with the belief dynamics of the agent. Finally, we apply our model to identify latent states in the behaviors of monkey performing a foraging task, and find clusters of latent states that identify periods of time consistent with expectant waiting. This data-driven behavioral model will be valuable for inferring latent cognitive states, and thereby for measuring neural representations of those states.

Introduction

An animal’s survival depends on effective planning for future costs and rewards. One of the most fundamental purposes of the brain is to create and execute such plans. However, these plans cannot be directly observed from behavior. To understand how the brain generates complex behaviors and learn how an animal builds a representation of the surrounding environment, it is valuable to construct hypotheses about the brain’s internal states that narrow the search space for neural implementations of planning. These hypotheses often come from models of the task implemented as artificial agents, whose internal state representations provided a latent space. However, differences between the model task and agent and the real task and animal create the potential for severe model-mismatch, injecting unknown biases into scientific conclusions. Here we use a latent-variable model to impute latent behavioral states based on observed behavior directly, using a data-driven latent-variable analysis that is designed to match the dependency structure of agent-based models without enforcing parametric structure.

To understand the mechanisms underlying behaviors, it is crucial to study hard tasks that involve inferring latent variables, since only then will an animal need to create a mental model of the world; otherwise the animal could perform well simply by responding to its immediate sensory input. Naturalistic foraging is one such task where an agent has to make decisions from many difficult choices in an uncertain environment. When foraging, an animal must take actions to procure rewards, and these actions have costs. How the animal schedules its actions determines the balance between total costs and rewards, Charnov & Orians (2006). The animal’s goal in foraging is to use its energy resources for short term and long term sustenance. Decisions must be made continuously, and therefore time is a key ingredient in foraging: An animal benefits from tracking when reward is likely accessible at different locations. A natural way to represent such temporal quantities is in terms of dynamic event rates. For this reason, our work highlights the continuous-time aspects of decision problems.

Fig 1 illustrates our motivation for the foraging problem. An agent develops an internal model and takes an action, which may result in a reward. As a result, the agent updates its internal model in an attempt to learn the environmental dynamics. We explore the plausibility that an animal’s internal states in continuous time manifest as measurable consequences on its behavior, using a switching hidden semi-Markov model, and demonstrate the model’s applicability in inferring latent states on a foraging task.

Figure 1:

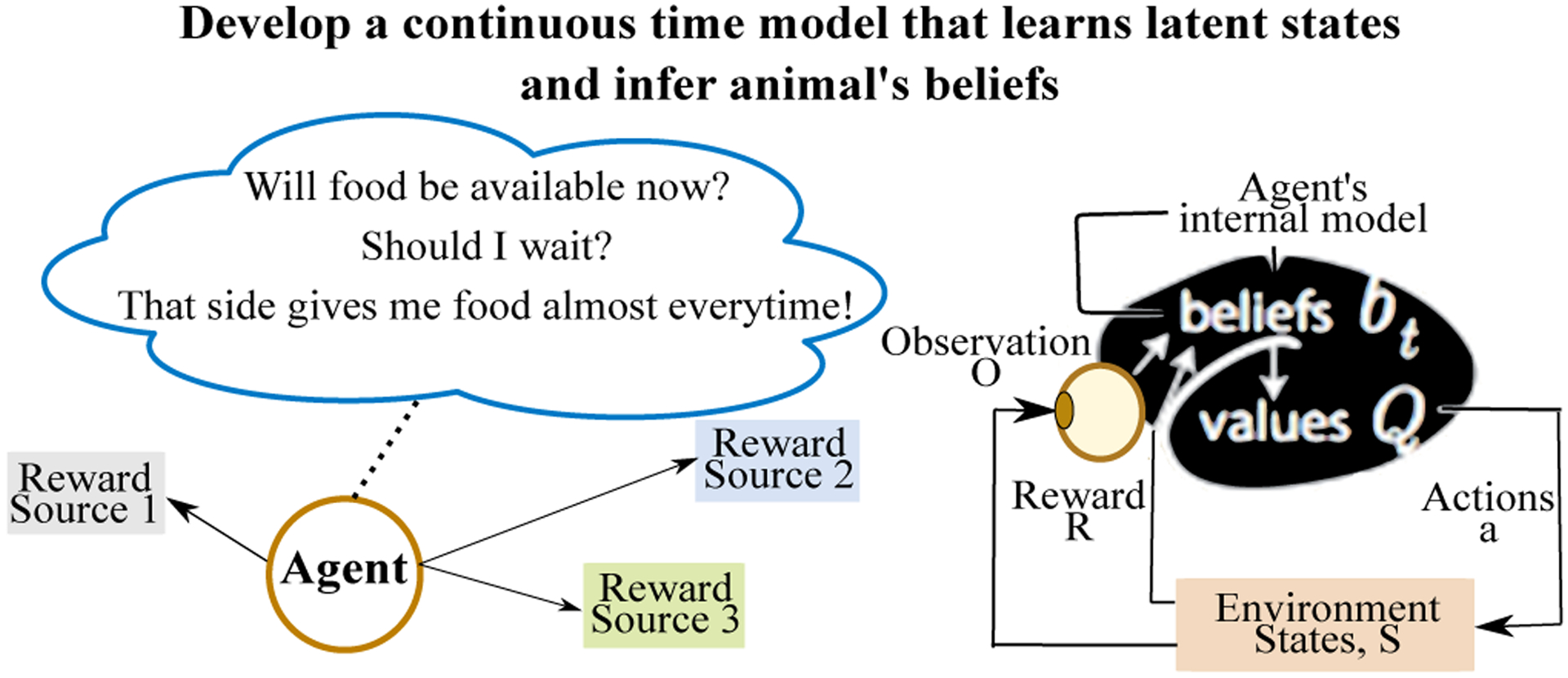
Overview: In complex natural tasks such as foraging, an animal faces a continuous stream of choices. Some of the choices pertain to hidden variables in the world, such as food availability at a given location and time. These variables determine time- and context-dependent rates for observation events and rewards. To perform well at these tasks, animals must learn these hidden rates and act upon what they have learned. Our goal is to develop a data-driven, continuous-time model for inferring an animal’s latent states and their dynamics.

In the remainder of the document, we provide background, discuss the presented model and procedure followed by the experiments, results and discussion.

Background

Behavior identification using computational models has a rich history, and clear value–the ability to learn rich representations of behavioral constituents provides important insights into underlying neural processes which can also be incorporated into the development of artificial agents (Anderson & Perona (2014)). Early behaviorists explored behavioral sequences in an attempt to learn determining causal factors underlying behavior, aiming to explain effects like when an agent switches to an alternate choice. These approaches are still common in animal ecology, where hidden Markov time series models (HMMs) have been used to analyse animal’s internal states Nathan et al. (2008); Langrock et al. (2012). Macdonald & Raubenheimer (1995) proposed using HMMs to capture causal structure in putative motivational states. However, they also observed that there are no one-to-one correspondences between the learned states and behavior, and Zucchini et al. (2008) found that behavior also influences internal states through feedback, challenging the dependency structure assumed by HMMs. To capture non-stationarity in behavior, Li & Bolker (2017) use temporally varying transition probabilities to model animal movement. However, behavior identification has struggled to produce more than a description of the behavior, with unknown relationships between the elicited latent states and the animal’s representations. These failures are less surprising when it’s realized the behavior expressible by HMMs is incompatible with key characteristics of observed behavior.

In these works and others, an important question left unanswered is what kind of latent belief states could be inferred that not only represent belief dynamics but also the choices that an animal or an agent makes. We attempt to uncover latent state beliefs in a continuous time model and apply it to a complex ecological process, foraging, which has multiple underlying sub-processes including satisfaction of needs, searching for alternatives, motivation, decision making, and control. We show that by generalizing allowing action-dependent transitions and more complex temporal dynamics, we can capture the expressivity of artificial agents designed for these domains, and highly interprable representations from animal behavior.

Model

Ecological behavior in animals is often well characterized by quick transitions between discrete behavioral modes. These transitions are difficult to predict from external events, and instead reflect a shift of the animal’s internal state based on integrating events over a longer time scale. A process with quick transitions separated by long inter-event intervals can be approximated by a discrete-time hidden Markov process involving transition probabilities, but many of the probabilities (those for which the state is unchanged) will be close to one, while the remaining probabilities will be very small and decrease with the discrete time scale. Instead, we expect there will be advantages in treating these latent dynamics in continuous time, based on rates or time intervals between transitions and events.

A natural model to account for these point-like transitions in continuous time is the semi-Markov Jump Process, Rao & Teh (2013). This process is a simple but powerful class of continuous-time dynamics featuring discrete states that transition according to a generator rate matrix, producing rich and flexible timing that is potentially better matched to animal behavior. In contrast, times of transitions between states in a Markov process are exponentially distributed, which describe animal behavior poorly.

However, agents who control their environment affect transition rates through their actions, which means a single generator rate matrix is not sufficient to model behavior. An important example are Belief MDPs, which is a representation of a Partially Observable Markov Decision Process (POMDP, Kaelbling et al. (1998)). POMDPs are a model for inference and control when sensory measurements provide only partial observations of the state of the world. Belief MDPs have distinct transition matrices that update beliefs differently for each action. Action-dependent transitions imply that a standard semi-Markov model with a single transition generator is not expressive enough to match action-dependent belief dynamics.

To allow for action-dependent belief dynamics, we propose a switching semi-Markov (SMJP) model that matches an agent’s belief dynamics by switching its generator depending on the action a: A_s′|s,a. Let $s\in S$ be a discrete latent state, and A_s′|s be an N × N generator rate matrix that can be interpreted as an instantaneous transition matrix Adt = P(s′(t + dt)|s(t)). This generator defines a point process that jumps from state s to s′ at time t according to the time-dependent matrix P_t = exp(At). The process can be implemented by sequentially sampling a time t_i(s_i) from the total rate leaving state s_i, followed by sampling a new destination state s′ according to the matrix P_ti(si)(s′|s_i) evaluated at this sample time (Gillespie’s algorithm Gillespie (1977)). An analogous process occurs for the generation of observable events o, through the emission generator matrix B_o|s. The resulting process is similar to a simple Markov process, except that the time between transitions is stochastic and depends on the starting state (but not the end state), illustrated in Fig 3; the animal’s behaviors and decision making are continuous, albeit partially observable only at discrete recording times.

Figure 3:

Comparison of graphical models of behavior. Left: In Belief MDP, belief transitions depend on actions selected by a policy. Center: Transitions in Semi-Markov Jump Process are independent of actions. Right: The Switching SMJP allows transition rates to depend on actions.

The Markov Jump Process extends discrete time Markov processes in continuous time. Rao & Teh (2013) introduced Markov chain sampling methods that simplify structures by introducing auxiliary variables. We adapt jump structures to provide a continuous-time representation for the free foraging task and the trajectory is introduced using a generator matrix. Let $A\in {ℝ}^{N\times N}$ be the generator matrix, which is skew symmetric and negative diagonal entries. We can represent $P_t\in {ℝ}^{N\times N}$ as continuous-time transition matrix given by P_t = exp(A_t), $B_t\in {ℝ}^{N\times N}$ as discrete time transition matrix that is induced by uniformization, and $L_t\in {ℝ}^{N\times \left|O\right|}$ as observation matrix P(O|s).

Uniformization instantiates the Markov Jump Process as a sequence of discrete time transition matrices (Fig 2), by introducing a latent sequence of random times that are adapted to the process generator but occur at a rate Ω ≥ max_s A_s. For each interval, a random discretization vector of sampled times is W = [w₁, w₂, …, w_n], and we impute sampled times for a trajectory. Using this notation, we sample both random times as a Poisson process with intensity Ω and states using the generator matrix. The hidden Markov model characterizes a sample path of a piecewise constant stochastic process over these sampled and event times as (s₀,S,T) where T is now an ordered union of event times and randomly sampled discretized times. The chain can jump from a state to the same state or any other state, while the emissions are observed only at certain specified times. Since we sample intervals with these virtual jump times, the constructed process represents the same chain.

Figure 2:

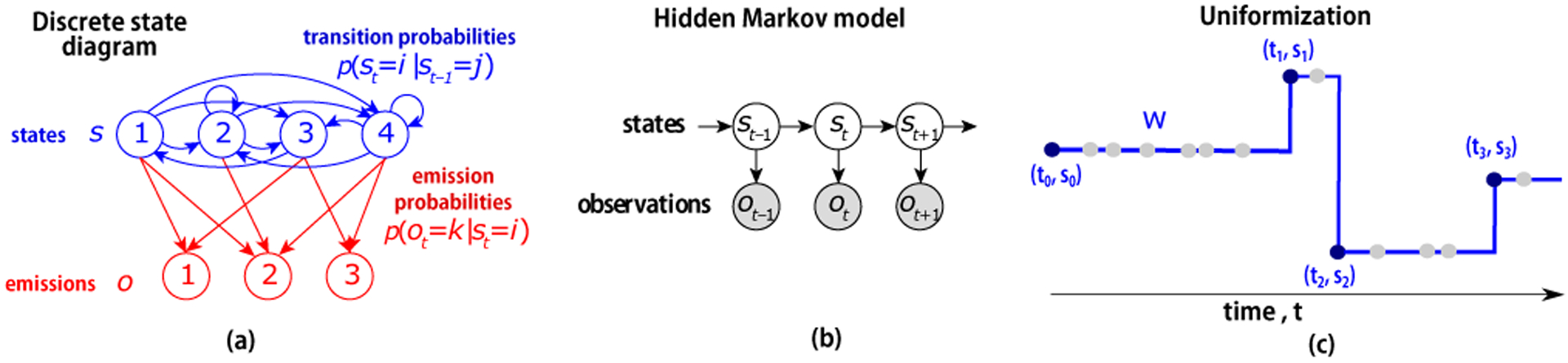
A discrete-state Hidden Markov Model. a: Discrete state diagram shows latent states (blue circles) and their transitions (blue lines), as well as the possible emissions from each state (red circles) with their emission probability (red lines). b: Directed probabilistic graphical model showing dependence of state variable s_t+1 and observation o_t on the previous state s_t. c: We present a continuous-time extension for latent states and discrete time observations using uniformization, Rao & Teh (2013)

To learn the discrete time transition matrix B and emission matrix L, we consider an ensemble of sample sequence of observed emissions as generated from an HMM, and update the matrices using an EM algorithm to best account for the available observations. However, if we sample discrete times once, the estimates would be biased, so we resample latent trajectories repeatedly and randomly based on uniformization. The learned B matrix is then used to update the generator matrix using the relation A_new = (B_new − I)Ω_old while preserving its structure, and the random times are resampled to adapt to the modified A_new. The resulting algorithm exploits uniformization to enable learning the generator via an EM-algorithm, which is orders of magnitude more efficient than Gibbs sampling.

Belief MDPs are a convenient representation for POMDPs that treats current beliefs (posterior probabilities) over partially observable world states as fully observable. Agents following a Belief MDP exhibit transitions between beliefs b_t+1 = f (b_t,a_t,o_t), take actions according to a policy π(a_t|b_t), and expect observations according to their beliefs via p(o_t|b_t) (Fig 3). The proposed SMJP model matches the agent’s action-dependent belief dynamics by switching its generator conditional on the action a: A_s′|s,a. To infer the agent’s model from experimental observations, we develop an EM algorithm to infer it’s parameters. When applied to our switching model, the forward α, backward β and update ξ equations of hidden Markov model, Rabiner (1989), can be written as:

$$\begin{gathered} {\alpha }_{t+1}^{k^{\prime }}(j)=\left[\sum _{i=1}^N{\alpha }_t^k(i)B_{ij}^k\right]L_j\left(o_{t+1}\right); \\ 1\le t\le T-1;1\le j\le N;1\le k,k^{\prime }\le K \end{gathered}$$ (1)

$$\begin{gathered} {\beta }_t^k(i)=\sum _{j=1}^N{B}_{ij}^k{L}_j\left(o_{t+1}\right){\beta }_{t+1}^{k^{\prime }}(j); \\ t=T-1,T-2,\dots ,1;1\le i\le N;1\le k,k^{\prime }\le K \end{gathered}$$ (2)

where k,k′ are the action switching indices at time t and t+1 respectively. We adjust the model parameters to maximize the probability of the observation sequence given the model and train using EM. Updates are made using the ξ variable, which is the probability of being in state i at time t and state j at time t+1, and is given as

$$\begin{gathered} {\xi }_i^k(i,j)=\frac{{\alpha }_i^k(i)B_{ij}^k{L}_j\left(o_{t+1}\right){\beta }_{t+1}^{k^{\prime }}(j)}{{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i^k(i)B_{ij}^k{L}_j\left(o_{t+1}\right){\beta }_{t+1}^{k^{\prime }}(j)}; \\ 1\le t\le T-1;1\le i,j\le N;1\le k,k^{\prime }\le K; \end{gathered}$$ (3)

The usual semi-Markov model is a special case of the switching semi-Markov model where the generator remains the same without action dependent switching. Our model is a switching model that changes rate, transition and emission matrices in accordance with the action taken by the agent. We learn the model using an EM approach , updating model parameters given transition times sampled by the uniformization process, and resampling the transitions given the new model parameters.

Procedure

We provide a brief description of the procedure, illustrated in Fig 4, that consists of pre-processing, initialization, training and validation steps. The overhead video, lever press and reward time sequences were used to set up observations and actions sequence required for training and validation. We processed the video recording using blob tracking to estimate position and velocity. Estimated positions and velocities were then clustered using k-means to assess different locations. By matching the time sequence of lever presses with the time sequence of locations, we augmented the observation space with locations. Therefore, the augmented observations for the model were lever press, reward delivery, and location. The actions were pressing either of the levers, stay at a location or move. The lever pressing actions were directly available from recording and we identified stay and move actions from the video location tracking. We defined similar observation and action spaces for simulations. To facilitate cross validation, we used a fixed 5-fold split to form training and validation sequences.

Figure 4:

Overview of the algorithm.

The proposed SMJP model has two main procedural components. The trajectorySampling function samples time intervals between consecutive observations using uniformization. It gives us imputed time sequences with missing observations within time intervals, allowing the model to transition between its hidden states at missing observations and use observations only at the end of the time interval. The switchHMM function implements EM approach using action switching and imputed sequences. We instantiated the transition, emission and rate matrices by training the model on observation and action sequences without imputed trajectories. Upon learning the emission and transition matrices for a sampled sequence, we use scaling factor, see model description, and make gradient like updates to the rate matrix while preserving its structure in the function GeneratorUpdate. The procedure of trajectory sampling and training on re-sampled sequence is repeated until the log-likelihood on held out data stops changing within a small tolerance. Therefore, we learn transition, emission probabilities and a rate matrix that capture the underlying continuous time process.

Experiment

We perform three experiments. We use the simulated toy data both to estimate a required training size and to ensure that the switching model is able to learn latent states, establish correspondence between partially observable Markov decision process belief states with SMJP latent states using theoretical optimal agent model and, then, apply our method to a real agent in a free foraging task. The number of states were selected by estimating the value at which the log-likelihood on the validation set stops improving.

Simulated toy data

To create a toy test data generated by the assumed model, we set up two transition matrices and one emission matrix with 5 states, 2 emissions and observation dependent actions. The expected size of the output sequence is set to 5000. Initial action is selected randomly and based on the action index, a transition matrix is selected. Thus, the selected transition matrix and emission matrix combination is used to estimate state transition and generate an emission. The observations, times and actions are added to the output sequence and the observation dependent action value is updated to get new observations. The simulated toy data sequence is used as a basic check if the SMJP model can learn and explain the observations. We fit SMJP model to the simulated data and observe that the log-likelihood starts stabilizing as it reaches the true number of states. It means that the model is able to explain the test data with an equivalent number of latent states (Fig 5). Therefore, we pursue a similar procedure to estimate the required number of latent states for both the optimal agent and the real agent.

Figure 5:

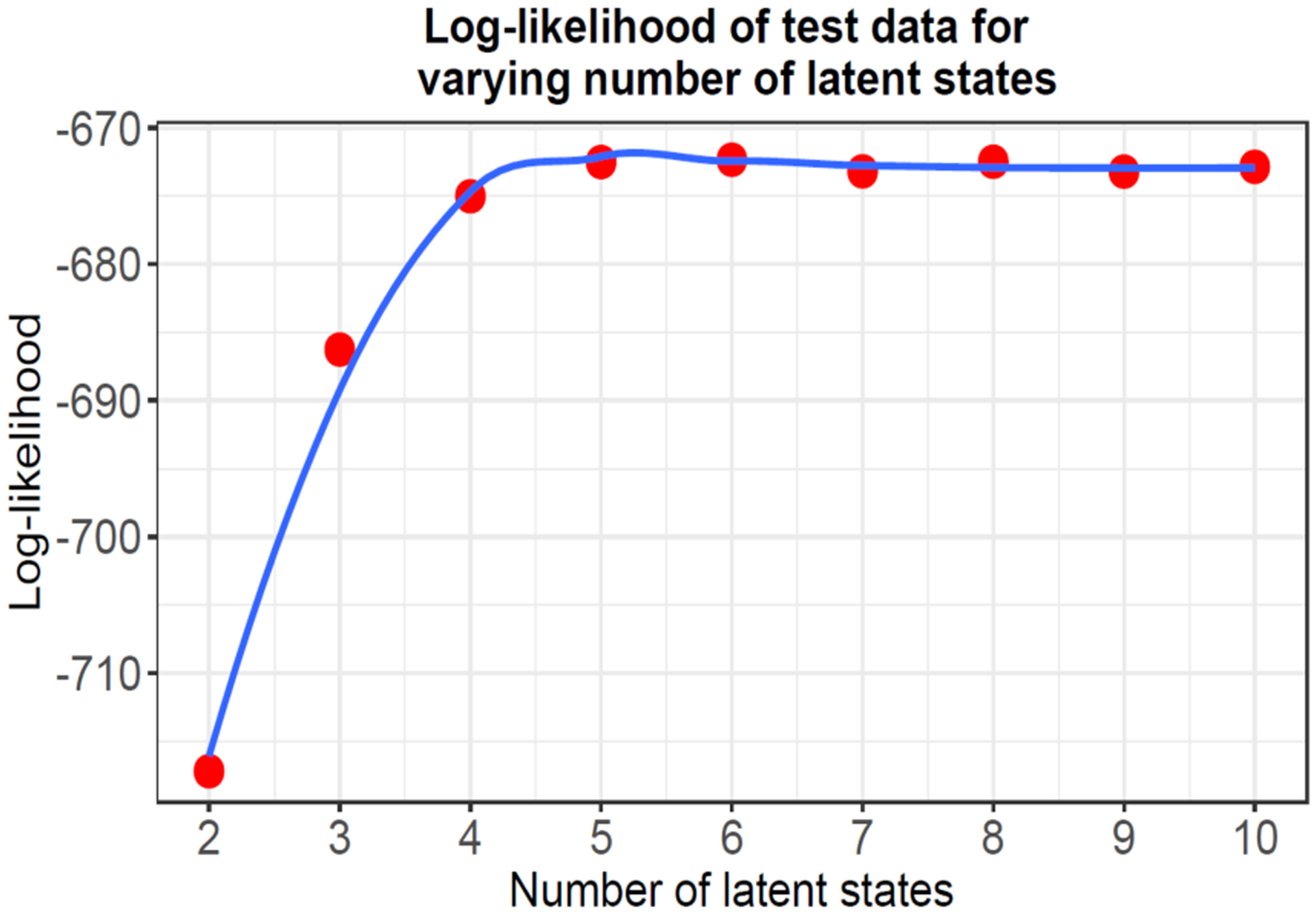
The model is able to explain simulated test data and the log-likelihood on held out data starts flattening out at the true number of states.

Optimal agent

To test our SMJP model we fit it on an optimal agent performing a foraging task. We model the beliefs of an ideal observer in this task using a POMDP. There is a one-to-one correspondence between a POMDP over partially observable world states z and a fully observed Belief MDP in which the ‘state’ is the ‘belief’ b or posterior distribution b_t = p(z_t|o_1:t) over the world state z. We solve this optimal actor problem using a Belief MDP on a discretized belief space. The agent keeps track of its belief state about the world following transition dynamics p(b′|b,a), where b′ is the new belief state, b is the current state, and a is an action. The agent’s sensory information depends on the world state according to the probability p(o|b,a). Upon taking action a, the agent receives immediate reward R(b,b′,a). The goal of the agent is to maximize the long-term expected reward $\mathbb{E}\left[\sum _{t=0}^{t=\infty }{\gamma }^{t}R\left(b_t,{b^{\prime }}_t,a_t\right)\right]$. Our model agent achieves this goal using a policy that solves for its policy Bellman (1957), by value iteration on the discretized belief states.

The beliefs serve as latent states which control the agent’s behaviors, and give its actions a non-exponential interval distribution, which is recapitulated by the fitted SMJP. We find that the likelihood of the observed data is maximal for a number of states that is smaller than the true size of the underlying POMDP belief space, indicating that the semi-Markov process is able to compress the agent’s dynamics into a smaller effective number of latent states. To validate the semi-Markov model in our foraging task, we discover the latent states of the artificial agent for whom we know the ground truth. We model this agent as a near-optimal actor that maximizes reward given partial observations of the true process. This agent maintains beliefs about the availability of food at different locations. Our agent is suboptimal because we do not store the beliefs with arbitrary precision, but rather discretize the beliefs to a finite resolution, and allow some diffusion between those belief states.

Application to the free-foraging task

We apply the SMJP model to infer latent states of agents performing a simple foraging task. We applied the model to both theoretical agents with near-optimal behavior, and real agents (macaques) whose behavior we measured experimentally. In this task, two boxes contained rewards that became available after random exponentially-distributed time intervals. If an agent presses a lever on one box when the food is available, that reward is released and that box timer is reset. The benefit of the reward is offset by two action costs: pressing the lever, and switching boxes. The state of the box is not observable, so the agent must choose its action based on an internal belief about the box, with the presumed goal of maximizing total reward minus costs. This internal belief constitutes a latent state that we infer using the semi-Markov process, both from the artificial agent and behaving monkeys.

We applied the SMJP model to infer latent states of macaques performing a simple two-box foraging task. The animal freely moved between two feeding boxes with levers that released food after an exponentially-distributed random time interval (mean of 10 or 30 sec) had passed. The model observations were lever pressing, reward delivery, and location within the box (Fig 7a). Actions were: stay, move, or press either lever. The monkey’s movements were tracked using overhead video, and quantized by k-means into different locations. The number of latent states is estimated by the log-likelihood maximization (Fig 7b). The resultant process constructs the monkey’s latent states to explain the non-exponentially-distributed intervals between lever presses (Fig 7).

Figure 7:

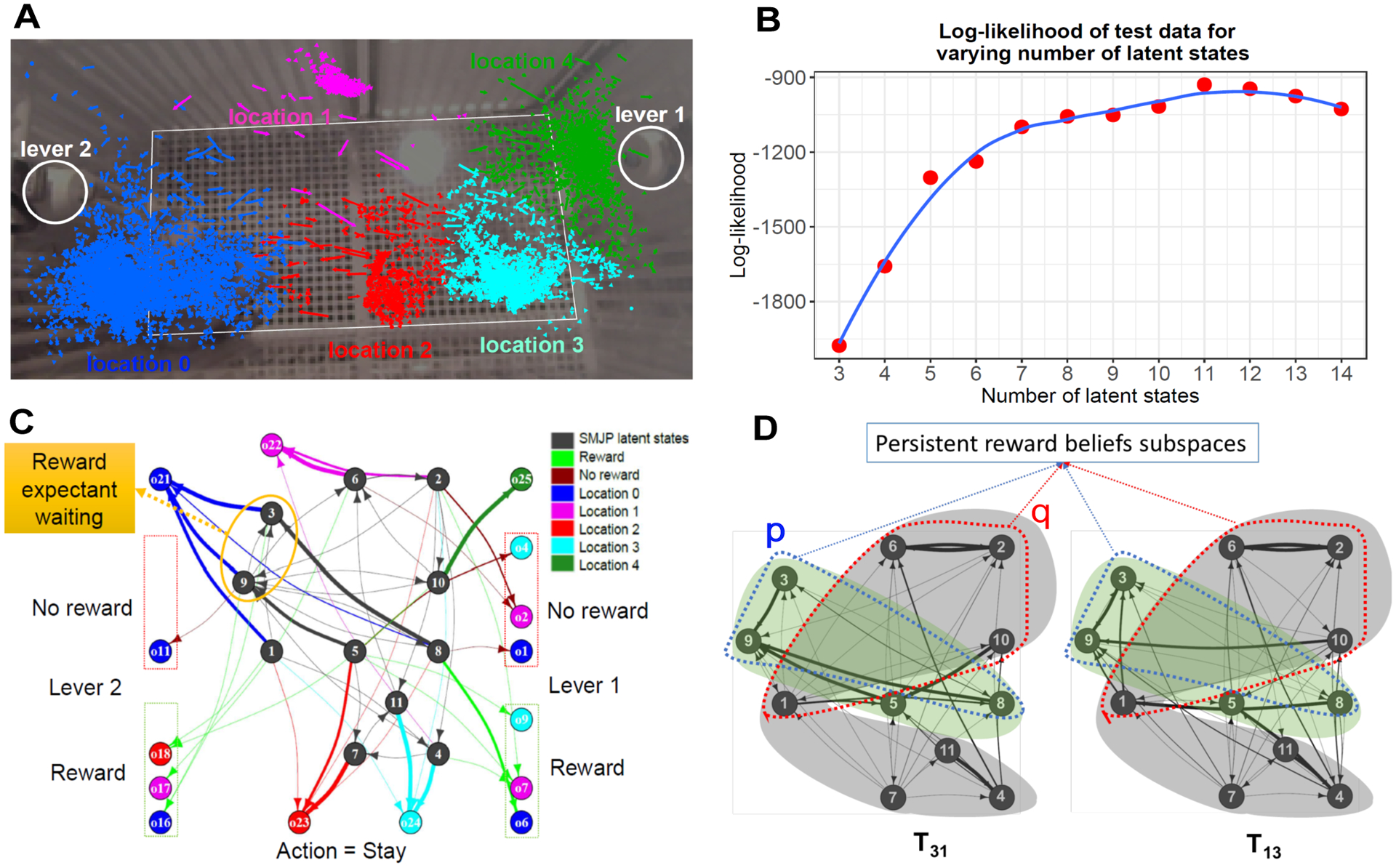
Analyzing behavioral data from a freely moving monkey using the SMJP. (a) Overhead video (background image) tracked the locations and normalized velocities (vectors) of the monkey. These data were then clustered by the k-means algorithm. (b) We get an estimate of the required number of latent states by observing log-likelihood on held out data. (c) SMJP model for observed monkey behavioral data for the action stay. Highlighted reward expectant waiting states illustrate that the latent states as regressors for the beliefs dynamics are useful in understanding monkey’s behavior. (d) Subspaces p and q (blue and red dotted), within the subgraphs (green and gray highlighted) for the joint operators T₃₁ and T₁₃ reveal persistent reward belief states.

Results and Discussion

Optimal agent

We trained the SMJP on an observation sequence generated by the optimal agent, and optimized the number of SMJP latent states by maximizing the log-likelihood of held-out data (Fig 6a). While the Belief MDP agent’s relevant states Z (including location, reward, and beliefs b) should be implicitly embedded in the SMJP latent states s, these two state representations are not immediately comparable.

Figure 6:

Latent states inferred by SMJP for an optimal agent implementing a POMDP. (a) Log-likelihood on held out data provides an estimate of the required number of latent states. (b) Co-clustering of states in a POMDP and our SMJP, based on the conditional probability of observing each POMDP state Z from each SMJP state, P(Z|s,obs). The POMDP states Z are depicted below the horizontal axis. Clustered structure in the plot reveals that the SMJP states have information about the agent’s belief dynamics.

To establish a correspondence, we compute the joint distribution over s and Z at any one time point using the shared time series of observations: $p(s,Z\mid obs)=\frac{1}{T}{\sum }_{t}p\left(s_t\mid o_{1:T}\right)p\left(Z_t\mid o_{1:T}\right)$. This joint distribution shows which SMJP and POMDP states tend to occur at the same time. It therefore provides a dictionary for translating the interpretable POMDP Z states into our learned and unlabeled SMJP s states.

To increase interpretability, we cluster p(Z|s,o) using information theoretic co-clustering, Dhillon et al. (2003), which provides a principled coarse-graining of the states with improved semantic interpretability. We determine the required numbers of SMJP and POMDP co-clusters by finding minimum information loss in information theoretic co-clustering. Fig 6b shows that latent SMJP states are associated with different belief states. Co-clustering also reveals that the SMJP latent states have dynamics that match the belief dynamics (not shown). These results demonstrate that the switching SMJP model can capture latent belief states and dynamics for behavioral data.

Real agent

We trained the SMJP on an observation sequence generated by the real agent (Fig 7a), and optimized the number of SMJP latent states by maximizing the log-likelihood of held-out data (Fig 7b). The SMJP model constructs latent states and dynamics using the real agent’s observations to predict choices and timing, including the non-exponentially-distributed intervals between lever presses. Fig 7c shows states extracted for the action ‘stay’. Beliefs precede an action and the extracted states reflect beliefs for the next action. For example, being in states 5,8 are rewarding to the monkey. States that can be interpreted as ‘expectant waiting for reward’ are highlighted (Fig 7c): these states form a self-exciting delay network that is activated from other rewarded belief states. Moreover, the lower entropy of latent states associated with lever 1 revealed guarding behavior we identified from video. Overall, the model network encodes a set of complex but interpretable dynamics of the animal’s beliefs and reward expectations which emphasize the complex computations underlying the decision making process.

Each transition matrix acts like an action operator and the real agent performs operations in sequences. So, we examine joint operators T_ji = T_iT_j, where T_i and T_j are operators for actions i and j respectively. We use an off-the-shelf package using, Brandes et al. (2008) to extract subgraphs and then persistent subspaces from all the six joint operators corresponding to different action pairs. Fig 7d shows subgraphs for two joint operators of interest (involving actions: lever press and stay). The latent states (within subspaces p and q) appearing in the same subgraphs of the joint operators illustrate the real agent’s persistent reward belief states. The states outside the subspaces p and q correspond to other beliefs, for example, switching. These results demonstrate that the presented model is able to extract subtleties, albeit complex, in the belief states and their dynamics. The extracted latent states and dynamics will be useful regressors for finding neural correlates of the computations underlying the monkey’s behavioral dynamics.

Conclusion

We presented a continuous-time switching semi-Markov model that learns the latent states dynamics in conformance with the belief structure of a partially observable Markov decision process. The revealed latent states are capable of inferring complex animal behavior and its belief dynamics in naturalistic tasks like foraging. Several aspects of the inferred behaviors and belief dynamics were examined to reveal that indeed, the internal latent structural representation match the agent’s belief structure. The data-driven switching semi-Markov model provides useful estimates of the structure of the internal latent states for hard tasks. The latent states from this behavioral model could potentially be used to understand correspondences between neural activity and the latent belief dynamics that govern how an animal selects actions.