Recent advances in point spread function engineering and related computational microscopy approaches: from one viewpoint

Abstract

This personal hybrid review piece, written in light of my recipience of the UIPAB 2020 young investigator award, contains a mixture of my scientific biography and work so far. This paper is not intended to be a comprehensive review, but only to highlight my contributions to computation-related aspects of super-resolution microscopy, as well as their origins and future directions.

The past

In 2008–2013, I was a graduate student at the Technion – Israel Institute of Technology. My research, under the supervision of Prof. Mordechai (Moti) Segev in collaboration with Prof. Yonina Eldar, dealt with recovering seemingly lost information in optical signals, such as phase and high spatial frequencies, by using the prior knowledge of signal sparsity (Shechtman et al. 2010; 2014a, b; Szameit et al. 2012). Towards the end of my studies, I took a class in 3D imaging, where I learned something fascinating, that would change the trajectory of my career: the point spread function (PSF) of an imaging system can be manipulated wildly, such that a point source no longer appears as a point at all—but rather as two points, with an orientation that depends on the distance of the source from the imaging system (Pavani et al. 2009) (Fig. 1). I was immediately hooked by this elegant method to encode depth information in a 2D image, and the simplicity of its implementation: placing a phase mask in the back focal plane of the imaging system. I asked the professor, Yoav Schechner, whether this PSF was the optimal shape to encode 3D information in a 2D image, not knowing at the time that this question would occupy my mind for the next few years.

Fig. 1.

The double-helix PSF encodes depth in the shape of the 2D PSF. Top: imaging setup consisting of an inverted microscope augmented by a 4F system with a phase mask (SLM) in the Fourier plane. Bottom: measured images of a fluorescent bead as it appears for different defocus values. Adapted from (Pavani et al. 2009)

After my PhD, I decided to take a step towards applying my optics and engineering background to biological problems, very broadly defined. I was fortunate enough to find a perfect place for this ambition: W.E. Moerner’s group at Stanford University. At Stanford, I started working on a beautiful system for single-molecule measurements based on electrokinetic trapping, known as the Anti-Brownian ELectrokinetic trap (ABEL) trap (Cohen and Moerner 2005; Squires et al. 2018; Wang and Moerner 2014). This is a system that enables observation of single molecule kinetics in solution over extended durations, by exerting force that negates their Brownian motion, keeping them trapped inside a small observation region. My plan was to apply compressed sensing (Candès 2006; Donoho 2006) to improve the photon efficiency of the trap. Quickly, however, it became clear to me that this system has been already engineered so well by previous group members, that my contribution will be marginal at best, and not worth the precious postdoc time.

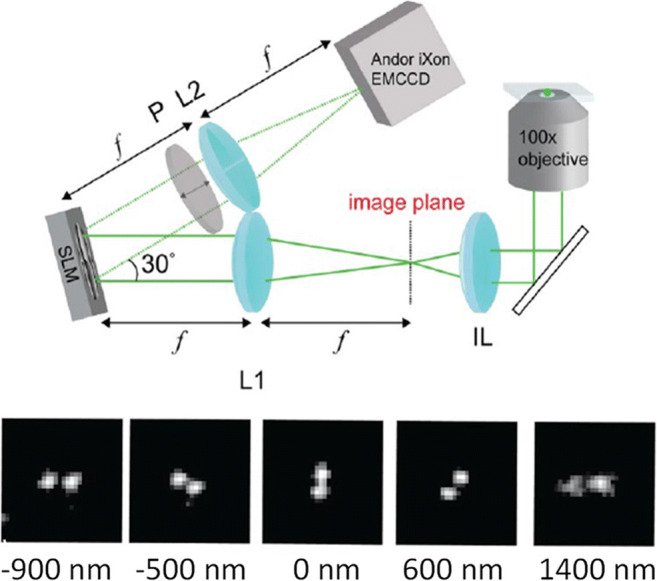
At the same time, I rekindled my interest in 3D imaging. The Moerner lab pioneered the use of sophisticated PSFs for 3D single-molecule microscopy (Backer and Moerner 2014; Backlund et al. 2012; Badieirostami et al. 2010; Pavani et al. 2009), namely, PSF engineering, and I became increasingly motivated to find the optimal PSF for 3D imaging. To briefly explain how PSF engineering works, a phase mask, e.g., an etched dielectric material or a programmable liquid-crystal spatial light modulator (SLM), is placed in the back focal plane (the Fourier plane) of a microscope (Fig. 1a). This acts as a phase filter for spatial frequencies, with the result being a modification of the PSF of the microscope, which can encode 3D information in the 2D PSF shape. Figure 2 shows several examples PSFs modified to encode depth information. Importantly, there is a mapping between the pattern on the phase mask and the resulting PSF. The mathematical relation is that the PSF is, to a good approximation, proportional to the absolute value squared of the Fourier transform of the phase pattern on the mask, multiplied by a depth-dependent defocus term (Petrov et al. 2017).

Fig. 2.

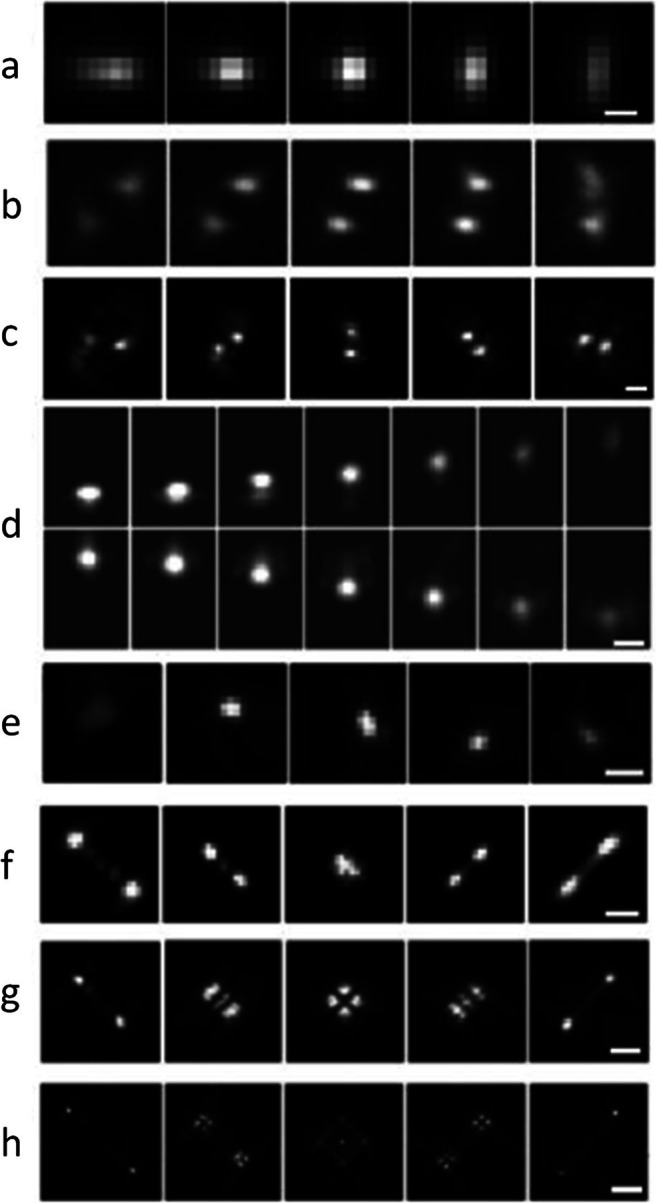
Example of measured PSFs encoding depth in their shapes, shown as a function of defocus; each PSF spans a different axial range. a Astigmatism (0.8 μm) (Huang et al. 2008). b Phase ramp (1 μm) (Baddeley et al. 2011). c Double-helix (3 μm) (Pavani et al. 2009). d Accelerating beam (3 μm) (Jia et al. 2014). e Corkscrew (3 μm) (Lew et al. 2011). f Saddle point (3 μm) (Shechtman et al. 2014a, b). g/h Tetrapod (6/20 μm) (Shechtman et al. 2015). Scale bars (a, c, d, e, f, g, h): 0.5, 2, 1, 1, 1, 2, and 5 μm. Figures adapted from Von Diezmann et al. (2017)

Different phase masks generate different PSFs. Some of these are useful for 3D imaging because they contain information on depth in their shape (Fig. 2), and some are exactly the opposite, extended depth of field PSFs (Ben-Eliezer et al. 2003; Dowski and Cathey 1995), where a point source looks pretty much the same no matter how defocused it is, within some axial range which is designed to be larger than the depth of field of the system. The question on my mind, therefore, was the one from my graduate class: what would be the optimal phase pattern to use in order to best encode the 3D position of a microscopic point source? The first step towards answering this question was to define it better.

Intuitively, a “good” 3D PSF is one that changes dramatically as a function of z, but also, importantly, does not spread the photons too much, otherwise it will be buried in the noise; namely, it should probably consist of some arrangement of spots. But how do you define this mathematically? After testing several unsuccessful definitions, in the sense that they led to no useful solutions (for example, minimizing the inner products between PSFs at different axial positions), I chose to focus on maximizing a mathematical quantity known as Fisher information (Kay 1995), which was shown earlier to be very valuable in single-molecule localization microscopy (Badieirostami et al. 2010; Ober et al. 2004). This quantity determines the lower bound on the variance of an estimated parameter from a set of measurements, using any unbiased estimator. In our case, this corresponds to a lower bound on localization precision. Simply put a PSF with high Fisher information is likely to exhibit better 3D localization precision.

We solved the optimization problem numerically, directing the computer to seek a phase pattern that would yield a PSF with maximal 3D Fisher information over a predetermined axial range. The result is the saddle-point PSF (Shechtman et al. 2014a, b) later extended to the tetrapod PSFs which exhibit larger axial ranges (Shechtman et al. 2015) (Fig. 2 f–h). Our 3D PSF optimization work was published in late September 2014, and 12 days later, it was announced that my advisor, W.E. Moerner, was awarded the Nobel prize in Chemistry for his pioneering work in single-molecule measurements. Overall, it was a good month.

Later, we realized it was also possible to encode color in the shape of the PSF of single molecules (Shechtman et al. 2016), a concept also used by other groups (Broeken et al. 2014; Jesacher et al. 2014). This made it possible to simultaneously image or track in 3D multiple-colored fluorescent emitters on a single optical channel, with no spectral filtering, and differentiate between them according to the shapes of their PSFs.

The present

In September 2016, I returned to the Technion in Israel as a PI, to start my lab in the department of Biomedical Engineering, as part of the Technion’s interdisciplinary program. The main mission of the lab is to develop optical and computational tools to observe life on the nanoscale. Research at this unique interface between engineering and the life sciences requires a highly interdisciplinary mixture of expertise, and I was fortunate to be able to assemble a team of excellent researchers with backgrounds ranging from physics, chemistry, biology, and engineering.

With the resurgence of machine learning and its amazing utility in a variety of image processing challenges (Dong et al. 2016; Kim et al. 2016; Rivenson et al. 2017; Wang et al. 2015), it was obvious that deep learning would be useful for solving difficult problems in super-resolution microscopy. Some of these directions I immediately started pursuing via a fruitful and ongoing collaboration with Tomer Michaeli from the Technion’s electrical engineering department.

First, we focused on single-molecule localization microscopy (SMLM). In SMLM, its most notable variants being (F)PALM and STORM (Betzig et al. 2006; Hess et al. 2006; Rust et al. 2006), the goal is to generate an image at super-resolution, namely beyond the resolution of the microscope, by sequential localization of blinking fluorescent emitters. Determining the position of a single fluorescent molecule from its PSF can be done to a precision much better than the size of the PSF, up to about an order of magnitude smaller, and so, if the molecules are labeling a structure of interest, this structure can be recovered computationally at a practical resolution of tens of nanometers (Hell et al. 2015).

One of the limitations of SMLM is that obtaining a single image requires the acquisition of a movie with typically thousands of frames, which limits the temporal imaging resolution to be on the order of minutes. This is because, traditionally, each frame must contain only a sparse subset of the emitters, to make image analysis feasible. To improve temporal resolution, therefore, a necessary condition is to handle localization of very densely spaced emitters, such that their PSFs overlap. Consequently, many methods have been developed to address the problem of overlapping emitters in SMLM (Barsic et al. 2014; Cox et al. 2011; Dertinger et al. 2009; Gazagnes et al. 2017; Holden et al. 2011; Huang et al. 2011; Hugelier et al. 2016; Qu et al. 2004; Sergé et al. 2008; Solomon et al. 2018; Zhu et al. 2012). Some of these methods can handle dense emitters very well, however, at the cost of long computation and a considerable amount of manual parameter tuning.

We developed a fast, precise, and parameter-free tool based on deep learning for dense emitter localization in SMLM, termed Deep-STORM(Nehme et al. 2018). The idea was to train a neural net to output super-resolved images from a large amount of simulated blinking movies. Advantageously, training on simulated data, with some adjustments using a small quantity of experimental data to refine the imaging model (Ferdman et al. 2020), proved to be possible. Also, since the training data consists of randomly positioned emitters, it does not use a priori structural information and is therefore inherently robust to different sample types.

The problem of emitter overlap is, naturally, even worse for 3D localization with engineered PSFs, because they are larger and therefore overlap even at lower densities. Therefore, we extended our deep learning approach to engineered PSFs with DeepSTORM3D (Nehme et al. 2020a, b). This is conceptually a more difficult task than 2D, because in 3D, different emitters exhibit very different PSFs, depending on their depths, whereas in 2D all emitter PSFs appear very similar. In fact, no existing algorithm was capable of handling such overlap of different PSFs; deep learning proved to be uniquely powerful in solving this difficult inverse problem, producing super-resolved 3D images of cellular structures from dense blinking frames using engineered PSFs (Fig. 3a–b).

Fig. 3.

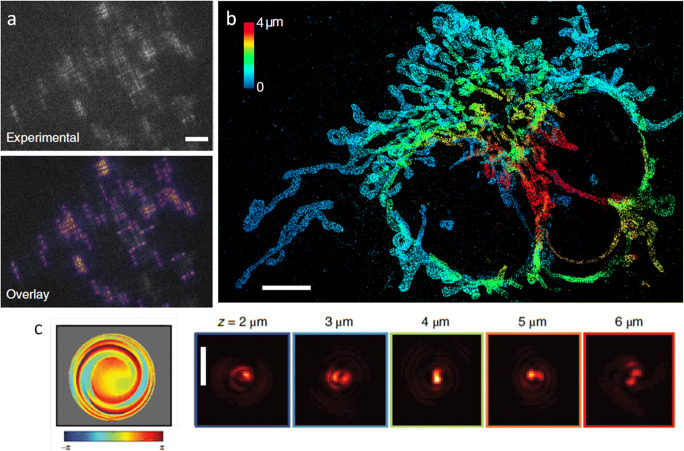
DeepSTORM3D solves the 3D dense emitter localization using a neural network. a Top: Example experimentally measured frame. Each shape (PSF) is a single fluorescent molecule. Bottom: Rendered frame from recovered emitters by the neural net. Scale bar: 5 μm. b Super-resolved mitochondria image from thousands of frames. Color encodes depth. Scale bar: 5 μm. c An optimal phase mask (left) and PSF (right) for dense emitters in 3D, learned by the neural net. Scale bar: 3 μm. Figure adapted from Nehme et al. (2020b)

Importantly, in DeepSTORM3D, we addressed another challenge that was unsolvable by standard approaches: how to design the optimal 3D PSF for a high density of emitters. While the Tetrapod (Fig. 2f–h) is optimal for localizing a single point source, it is laterally large, and therefore would cause severe overlap for multiple adjacent PSFs. It is reasonable to think that a PSF with a smaller lateral footprint would perform better for dense localization. But, how to find the optimal PSF for dense localization? This is not an easy task to solve with classical methods such as Fisher information maximization, because that would require considering numerous individual cases of spatial overlaps and emitter quantities. Therefore, to engineer the optimal 3D PSF for dense localization, we trained a neural net to jointly optimize the phase mask alongside the image recovery part, by training on many instances of randomly and densely positioned emitters. The resulting PSF is shown in Fig. 3c. Interestingly, it exhibits some rotation as well as asymmetric axially dependent spreading—known attributes of previously developed depth-encoding PSFs.

We recently extended the DeepSTORM3D PSF design approach to a two-channel system (Nehme et al. 2020a, b), which is advantageous at very high emitter densities—where the two channels are synergistically used to encode complementary information. In a similar manner, we have also derived the optimal multicolor PSF, namely, a wavelength-dependent PSF, that optimally encodes the colors of point emitters in a grayscale image (Hershko et al. 2019). Nowadays, deep learning has become an extremely useful tool in super-resolution microscopy, with a variety of applications ranging from single-image super-resolution to depth imaging (Belthangady and Royer 2019; Ouyang et al. 2018; Weigert et al. 2018; Zhang et al. 2018), with ever-increasing accessibility to non-expert end users (von Chamier et al. 2020).

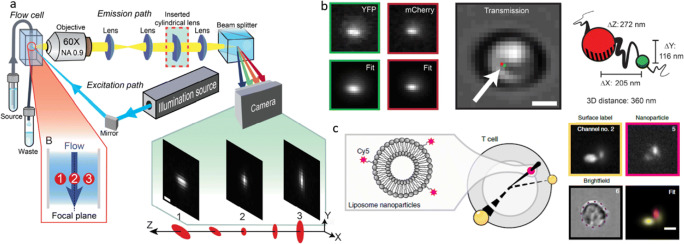
A daunting challenge in 3D microscopy is that of limited throughput; Obtaining a 3D image is typically more time-consuming than obtaining a 2D image, especially when it necessitates scanning. Notably, there are methods to image objects at high rates—a particularly successful one is imaging flow cytometry (Basiji et al. 2007; George et al. 2004; Kay et al. 1979; Kay and Wheeless 1976), where cells are flowing in a microfluidic channel and are imaged as they move through an illuminated region. This typically produces a single 2D image per cell, although light sheet microscopy and holography have been incorporated into image flow cytometry (Dardikman et al. 2018; Gualda et al. 2017; Sung et al. 2014; Wu et al. 2013). Recently, we combined imaging flow cytometry with PSF engineering, to enable 3D co-localization inside live cells at a very high throughput of thousands of cells per minute. This was achieved by integrating a phase-modulating element (we used both a cylindrical lens and a phase mask) inside the imaging path of a commercial imaging flow cytometer (Weiss et al. 2020). This encoding of depth information enabled gathering large statistics about 3D co-localization over short periods of time. We used our method to demonstrate the characterization of physical distances between two labeled DNA loci in live yeast cells, dynamically on a population scale, as well as quantification of cellular entry of nanoparticles designed for therapeutic delivery by Avi Schroeder at the Technion (Fig. 4).

Fig. 4.

Imaging flow cytometry with PSF engineering. a Flow imaging setup, incorporating a cylindrical lens to encode depth via astigmatism. b Measuring 3D chromatin compaction in live yeast cells, using a 2-color fluorescent operator-repressor system for DNA labeling. Scale bar: 2 μm. c Localizing liposome nanoparticles (pink spots) in human T lymphocyte. Yellow spots represent surface-adhered fluorescent beads, encoding the 3D spherical cell shape. Scale bar: 5 μm. Figure adapted from Weiss et al. (2020)

Another application where deep learning has proved to be powerful is extracting information from challenging single-particle tracking data (Dosset et al. 2016; Granik et al. 2019; Kowalek et al. 2019; Muñoz-Gil et al. 2020). A common problem in particle-tracking experiments is that the acquired trajectories can be very short, e.g., due to photobleaching, and therefore, deriving statistical information from them can be difficult. In a collaboration with Yael Roichman from Tel Aviv University, we trained a neural net to classify single-particle trajectories by the type of diffusion—Brownian, fractional Brownian, or continuous time random walk (Granik et al. 2019). A main advantage of our deep learning approach is that it outputs an accurate classification from a relatively small number of steps (~ 25) and can also efficiently handle sets of multiple short trajectories—which is often the only kind of available data.

The future

The field of computational microscopy, in which the captured image need not bear any resemblance to the desired image, holds tremendous potential for capturing seemingly hidden data in biological samples. Freeing microscopes from the burden of generating images that are appealing to the human eye opens up fascinating degrees of freedom.

Specifically, neural nets successfully tackle various challenging inverse problems in microscopy, such as denoising, clustering, volumetric imaging, and more (Belthangady and Royer 2019). However, beyond their use in image analysis, an extremely appealing application for neural nets is in optical design, i.e., learning an optimal imaging system for a specific task. This is especially powerful when the route towards optimizing the design metric is unclear: How would one rationally design an optimal depth-/color-encoding PSF for dense emitters in 3D (Hershko et al. 2019; Nehme et al. 2020a, b), or an optimal illumination system for diagnosing malaria in blood smears (Muthumbi et al. 2019)? How does one achieve fast and robust autofocusing (Pinkard et al. 2019)? These are questions that neural nets are already answering, and they are likely to continue to contribute to related areas.

Our research group will continue to pursue various directions in computational microscopy development, as well as to apply existing techniques to possible bio-medical applications; these include observing chromatin dynamics in live cells by single-particle tracking (Nehme et al. 2020a, b), developing diagnostic tools for bacterial growth detection (Ferdman et al. 2018), dynamic microscopic surface profiling (Gordon-Soffer et al. 2020), and sensitive bio-molecule measurements.

Funding

The author received support from the Zuckerman foundation; from the various funding agencies for the work presented here; and from the private companies, philanthropists, and tax-paying citizens of Israel, the USA, the European Union, and other countries who ultimately pay for this work.