Figure 3.

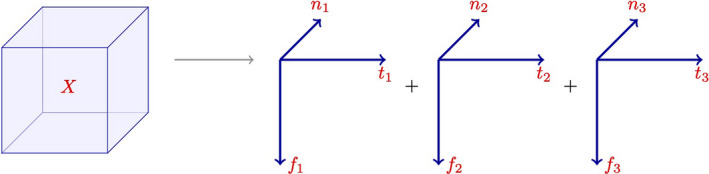
Theoretical canonical polyadic decomposition for tensor X from Figure 2. The outer product of each of the f_i × t_i vectors produces a wavelet power spectra and each of the n places has a score in the n_j vector specific to that wavelet power spectra. In this way we can use the three rank one tensors to approximate the original power spectra for each of the n original places. We can think of the matrix formed by the outer product of t_i × f_i as a component in the principal component analysis sense. Where each entry in the matrix determines the loading of the that time, frequency value. Each entry in the n_j vector represents a place‐specific score which determines the contribution of that matrix in the final wavelet power spectrum