Multi-Scale White Matter Tract Embedded Brain Finite Element Model Predicts the Location of Traumatic Diffuse Axonal Injury

Abstract

Finite element models (FEMs) are used increasingly in the traumatic brain injury (TBI) field to provide an estimation of tissue responses and predict the probability of sustaining TBI after a biomechanical event. However, FEM studies have mainly focused on predicting the absence/presence of TBI rather than estimating the location of injury. In this study, we created a multi-scale FEM of the pig brain with embedded axonal tracts to estimate the sites of acute (≤6 h) traumatic axonal injury (TAI) after rapid head rotation. We examined three finite element (FE)-derived metrics related to the axonal bundle deformation and three FE-derived metrics based on brain tissue deformation for prediction of acute TAI location. Rapid head rotations were performed in pigs, and TAI neuropathological maps were generated and colocalized to the FEM. The distributions of the FEM-derived brain/axonal deformations spatially correlate with the locations of acute TAI. For each of the six metric candidates, we examined a matrix of different injury thresholds (th_x) and distance to actual TAI sites (d_s) to maximize the average of two optimization criteria. Three axonal deformation-related TAI candidates predicted the sites of acute TAI within 2.5 mm, but no brain tissue metric succeeded. The optimal range of thresholds for maximum axonal strain, maximum axonal strain rate, and maximum product of axonal strain and strain rate were 0.08–0.14, 40–90, and 2.0–7.5 s⁻¹, respectively. The upper bounds of these thresholds resulted in higher true-positive prediction rate. In summary, this study confirmed the hypothesis that the large axonal-bundle deformations occur on/close to the areas that sustained TAI.

Introduction

Traumatic brain injury (TBI) is the most common cause of cognitive and behavioral deficits in the United States and worldwide and its rate is increasing every year.¹ Despite ongoing efforts to address and decrease TBI, it is still alarming that ∼1.4 million TBIs occur in the United States each year.² To reduce the number and severity of TBIs, more effective head protective devices and TBI risk reduction and prevention strategies are needed. Finite element models (FEMs), which can provide insights into tissue responses during biomechanical events experienced by the intact head, are among the tools that can play an important role in accelerating technical innovations in head protective equipment and improving TBI diagnostic and prognostic techniques. FEMs have the potential to determine tissue injury thresholds and predict the possible presence, degree, location, and distribution of injury after an incidental event.^3–13 Most of the previous FEM studies have focused mainly on predicting the absence or presence of TBI rather than estimating the extent and/or location of injury.^{3,4,6–10,12}

Prediction of brain regions and/or areas that might have sustained damage after a head impact or rapid rotation can greatly improve TBI diagnosis and treatment strategies and better guide advancement in the design of more effective devices to mitigate the occurrences and severity of TBI. An important question is whether and how closely and accurately FEMs can predict the actual location of brain injury. A practical approach to answer this question is to compare the pattern and location of predicted maximal dynamic biomechanical responses of the brain tissue during an event with the measured locations of injury.

The TBI research community has recently started to explore possible correlations between the outcomes of FEM simulations and location of injury.^5,11,14–18 For example, Ghajari and colleagues¹¹ reconstructed three common biomechanical events that can result in TBI and compared the distribution of the brain strain and strain rate at the boundary of the gray and white matter with the pattern of diffusion tensor imaging (DTI) abnormalities observed in a cohort of TBI patients. They found a correlation between the locations of highest brain tissue deformations induced by the three TBI loading scenarios that they examined and the common locations of imaging features in TBI patients.¹¹ In a study by our group, we reconstructed a set of real-world infant fall-related TBI accidents that resulted in skull fractures and found an agreement between the distribution of finite element (FE)-derived stress and strain in the skull and the location and pattern of skull fracture identified in the corresponding computerized tomography (CT) scans.⁵ In another study, Fahlstedt and colleagues¹⁴ quantified the correlation between the FE-derived brain-strain distribution patterns in three bicycle accident simulations and the hemorrhagic contusion patterns indicated in the image scans. A couple of studies also reconstructed fall-related TBI accidents that resulted in subdural hematoma and focused only on the regions of brain elements that were associated with the area of hemorrhage, as indicated by the corresponding CT scans.^15,16 Some animal studies also found the regional distribution of FEM-derived brain tissue strain and stress to be comparable with the pattern of contusion and cell membrane damage observed experimentally after controlled cortical impact.^17,18

All these studies demonstrated the utility of FEMs for estimating the location and pattern on injuries. However, most of these studies^5,14–18 focused on focal injuries such as skull fracture, hematoma, and contusion, which are observable lesions at the macroscopic level that can be localized using conventional neuroimaging scans. However, we are unaware of a study that examined spatial correlation of FEM results with diffuse soft tissue damage such as diffuse traumatic axonal injury (TAI). Performing such a study is challenging because it requires the whole brain to be explored rather than specific selected areas of interests, attributable to the diffusely dispersed nature of TAI. Another challenge is the absence of observable definitive macroscopic pathology on the current imaging scans specifically in the case of mild-to-moderate TAI. Although advanced neuroimaging modalities, such as diffusion tensor imaging (DTI), susceptibility-weighted imaging, and functional magnetic resonance imaging, have offered potential for improved evaluation and general diagnosis of TAI,^19–22 these techniques have not yet attained sufficient diagnostic criteria^20–22 for a definite localization of TAI pathology.

Animal models of TBI, in which the precise location and extent of TAI are available through microscopic histopathology analysis after euthanization, are great surrogates to investigate a possible correlation between the FEM results and the brain areas that TAI might have occurred. Moreover, the FEM studies in the TBI literature were mainly performed at the macroscale continuum level^{3–6,11,16–18} and lacked the responses of axonal fibers at the micro-/mesoscopic levels where axonal damage occurs and are detected by histopathology. Incorporation of axonal tract details and multi-scale modeling, where kinematic loading experienced by the head can be applied at the macroscopic level and deformation responses can be computed at the micro-/mesoscopic level, can bridge this gap and improve the axonal damage location prediction of FEMs.

Recent developments in FEMs set the stage for simulation of axonal damage by incorporation of the axonal orientations into the FEMs using the DTI technique.^{3,7,9,10,12,13,23} In most recent studies, the tract-oriented approach was used, in which the brain tissue was modeled with an isotropic or fiber-reinforced anisotropic^{3,6,10,23–25} material, and the brain biomechanical responses in the dominant direction of axonal tracts at each brain element were calculated. Although the tract-oriented approach has shown to improve the biofidelity of the FE brain models^6,10 and their injury prediction capability, some simplifications made in that approach resulted in a loss of anatomical information from the axonal tracts and a reduction in the biofidelity and accuracy of the derived axonal biomechanical response. First, for each brain element, one dominant fiber direction was estimated by averaging the fiber orientations of all DTI voxels within that element. These averaged orientations may not necessarily be aligned with the exact orientations of several axonal fiber bundles within that brain element. Second, in some of these studies that used isotropic material model for the brain tissue, the averaged axonal tract orientation in each brain element was determined in the initial undeformed condition and does not take into the account the change of the orientations of axonal tracts with respect to brain tissue given that the brain tissue deforms during the simulation.

More recently, an element embedding approach has been used in a few TBI FEM studies.^{12,13,26–29} This approach overcomes the simplifications of the tract-oriented method by including multiple fiber paths in each brain element. The element-embedding method allows for a coupled modeling of meso features of axonal structures within the three-dimensional (3D) macroscale brain FEM.

The objective of this study was to investigate the utility of such a multi-scale FEM approach to estimating the location of axonal injury. We hypothesized that the distribution of large FEM-derived brain tissue/axonal fiber deformations colocalize with the pattern of TAI. To that end, an embedded axonal tract pig brain FEM was utilized to simulate a set of well-characterized rapid non-impact head rotation (RNR) pig TBI experiments. The spatial distributions of induced TAI in those pig experiments were precisely quantified by histology, and TAI maps were generated and colocalized to the results of FEM simulations. An optimization method was then developed and coupled with the k-fold cross-validation technique to quantify the capability of different FE-derived tissue deformation parameters in estimating the location of axonal injury. The optimal FE-derived tissue injury thresholds and distance to actual TAI were determined and the threshold values were compared with the injury thresholds from in vitro and in vivo studies. This study demonstrates the capability of coupled meso-/macroscale FEMs in localization of axonal injury at the micro-/mesoscopic levels diffusely throughout the brain.

Methods

Animal model of traumatic brain injury

A well-characterized RNR pig TBI model^30–34 was used to produce a single rapid sagittal or axial head rotation causing purely inertial TAI. This TBI model produces unconsciousness, sustained cognitive dysfunction, and bilateral diffuse axonal and hemorrhagic injury.

In this experimental model of TBI, the animal was anesthetized and, while maintained on isoflurane, the animals' heads were secured to the inertial loading apparatus by a snout clamp. The lower part of the clamp, a metal plate covered with a rubber bite plate, was inserted into the animal's mouth and the head was secured by tightening the padded steel spring bands, which encircle the snout onto the metal plate. Immediately before injury, anesthesia, supplemental oxygen, and mechanical ventilation were withdrawn, and the piglet could breathe spontaneously on room air. Then, the pig head rotated through a 60-degree sagittal arc or 90-degree axial arc in 10–40 ms using an inertial loading device. The angular velocity of the pig head rotation was directly measured at 10 kHz, filtered with a fourth-order, low-pass Butterworth filter, and extracted for FE simulations. After injury, the piglet was removed from the bite plate, supplemental oxygen was resumed as needed, isoflurane was discontinued, the piglet was extubated, and stable monitors were discontinued.

All protocols for these experiments were approved by the Institutional Animal Care and Use Committee of the University of Pennsylvania (Philadelphia, PA), where these experiments were previously conducted. For this study, an experimental dataset containing 16 two-month-old and 26 four-week-old pigs with head rotation in the axial or sagittal plane was selected.

Neuropathology analysis

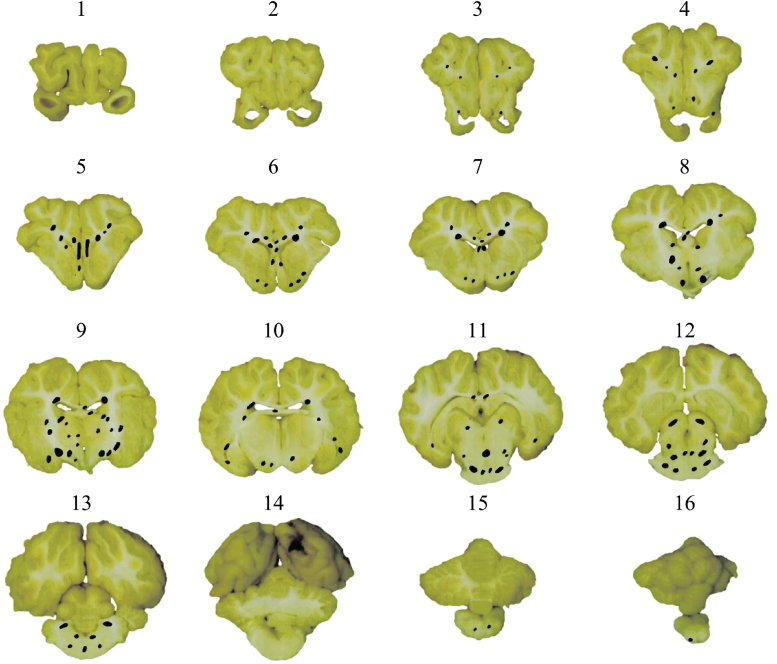
These animals were euthanized at 6 h post-injury, and their brains were perfusion-fixed and sectioned in 3-mm coronal slices (14–22 slices per brain). All coronal brain sections were then photographed, cut into 6-μm-thick slices, and stained for beta-amyloid precursor protein (βAPP; at a dilution of 1:5000), which is a gold-standard marker of damaged axons. For each slice, areas (20 × field size, 0.586 mm²) with at least two positive βAPP immunostaining axonal damage profiles were marked as TAI areas and neuropathological maps were generated. An example of TAI maps for one of the animals is given in Figure 1. The cumulative sum of marked areas of TAI over the whole areas of the examined brain slices (every 3 mm throughout the whole brain) was used to calculate the axonal injury volume (AIV), which indicates the severity of axonal injury. The range of AIV calculated for this dataset is 0.02–1.65%, which represents a no/very minor-to-moderate level of axonal injury.

FIG. 1.

Traumatic axonal injury (TAI) maps at every 3 mm throughout the whole brain for 1 piglet. For each slice, areas of TAI were identified by βAPP immunostaining analysis and marked at each brain slice (black marks). βAPP, beta-amyloid precursor protein. Color image is available online.

Anisotropic axonal tract embedded pig head finite element model

A 4-week-old pig head FEM consisted of brain, falx, skull, and brain-skull connectors (mimicking the relative motion of brain to skull), previously developed and validated by our group,^3,4 was recently enhanced by adding anatomical regions, including lateral ventricles, corpus callosum, and white matter, through mapping the coronal slices of the FEM to the corresponding brain coronal CT images.^12,13 In addition, axonal fiber tract structures were reconstructed by streamlines tractography analysis using a previously acquired DTI scan of an uninjured perfusion-fixed ex vivo 4-week-old piglet brain.³

Fiber tractography analysis was performed in the Advanced Normalization Tools (ANTs) and Camino software packages,³⁵ using a Euler method with linear interpolation algorithm by the tracking stop criterion of fractional anisotropy (FA) <0.2 and the tract-turning angle threshold of 60 degrees, and the fixed step size of 0.2 mm. FA value was calculated for each seed point through all streamlines. The axonal tractography streamlines were then used as an input, and the axonal fiber bundle structure FEM was developed using a custom MATLAB script (V. R2015; The MathWorks, Inc., Columbia, MD) and embedded into the pig brain FEM with *CONSTRATNED_BEAM_IN_SOLID Keyword in LS-DYNA (v 971 R9.2.0; LSTC, Livermore, CA). The new enhanced pig FEM, shown in Figure 2, consists of 13,189 brain, 110 lateral ventricle solid elements, and 72,842 one-millimeter one-dimensional axonal fiber beam elements. The average of FA values of streamline seed points along the element was assigned to each axonal fiber element. The axonal fiber elements were categorized into eight groups depending on the FA value of the element as shown with different colors in Figure 2.

FIG. 2.

The embedded white matter tracts pig brain finite element model. In the top figure, the model was cut at several points for illustration of the components. The bottom figure shows the axonal fiber tract within the head geometry. FA, fractional anisotropy. Color image is available online.

The brain tissue was broken down into axonal fiber and isotropic brain matrix. The brain and axonal fibers were modeled using a modified version of the anisotropic Holzapfel-Gasser-Ogden hyperviscoelastic material model^12,29 and a one-term Prony viscoelastic material,³⁶ as described in detail in the Supplementary Appendix and implemented in LS-DYNA using user-defined material models. The coefficients of the material model of the matrix brain tissue were computed based on a published material testing data of pig brain tissue.³⁶

The material property of axonal fiber bundle was computed using an effective stiffness ratio (R_v) based on the fiber to brain volume fraction (${\gamma }_V$) and stiffness ratios (see the details in the Supplementary Appendix or a previous work¹²) experimentally determined for pig brain.³⁷ The effective stiffness ratio was used to prevent potential volume redundancy and excessive material stiffness that may arise by the embedded FEM approach,^12,29 in which the brain matrix covers the whole brain volume including the volume of embedded fibers.

To minimize the possible effect of mass redundancy which may arise by the element embedding method, a very small density (ρ = 0.00104 g/cm³), which is 0.001 of the brain density, was used for the embedded axonal fiber elements in this model.¹² The total additional mass of the embedded axonal bundles is only 5*10^–4 of the original brain mass and thus its effect is negligible. The cross-section of 0.43 mm² was used for the axonal fiber elements to obtain the axonal fiber/brain matrix fraction of 0.5 that was experimentally identified by Arbogast and Margulies³⁷ for pig brain.

The material property of the eight groups of the axonal fiber elements, assuming similarity between mechanical anisotropy and diffusion anisotropy, was adjusted using a dimensionless structure parameter (κ ; details in earlier works^12,38,39 and the Supplementary Appendix) that accounts for the orientation distribution of the axons in a voxel-scale fiber bundle and can be related with FA values of the fiber bundle elements. It should be noted that in this model the axonal fibers only contribute during tension, but not compression. The detailed material models and coefficients used in this pig FEM for the axonal fiber bundles, brain tissue, skull, lateral ventricle, skull-brain connectors, and falx are given in the Supplementary Appendix of this article and also can be found in our previous work.¹² The mesh size of 1 mm was used for the axonal fiber elements, which is relevant to the brain elements with mesh size of 1.3–2.0 mm. To determine how sensitive the response of the brain model to the fiber element size is, smaller (0.5 mm) and larger (2 mm) mesh sizes were used for fiber elements and the cumulative axonal strain responses of the model with these three mesh sizes were compared (Supplementary Fig. S1), and no difference was observed.

The brain tissue deformation responses of this axonal tract embedded brain FEM were then validated against the brain deformations measured in an ex vivo hemisection experiment previously performed in our laboratory in high strain and strain rate similar to the pig TBI experiments (details published previously^3,12), and the FEM-derived brain deformation cumulative distribution curve was correlated with the curve obtained from the experiment with no significant statistical difference (p value, >0.05). Obtaining a realistic overall brain tissue deformation response was the objective of this validation process. It is worth mentioning that a similar validation approach was used for the previous pig brain models^3,4 from our group by comparing their overall deformation responses with the deformation captured by the same ex vivo pig hemisection experiments. Therefore, although different constitutive material models were used in this study and the previous pig brain models from our group and direct comparison between their coefficients are not possible, the brain material of these models provide similar deformation responses.

In addition, in this study, in order to investigate the effect of embedded axonal fiber bundles on the material behavior of the brain model, the deformation responses of the current anisotropic axonal embedded model was compared with an isotropic brain model with the same mesh properties and a brain visco-hyperelastic constitutive material model as the model in this study, but without the embedded axonal beams. The brain tissue material properties of the isotropic model were calibrated by adjusting the material coefficients of the brain tissue used in this study (multiplying G and k₁ by a ratio) until statistically similar deformation responses were obtained between the isotropic and axonal embedded anisotropic FE models (see Supplementary Fig. S2 in the Supplementary Material). The ratio of 1.3 was found for this calibration, suggesting that the embedding axonal bundles stiffen the brain response by 30% (ratio = 1.3).

Overall, the material property used for this pig model was softer than the ones used in the human brain models in the literature, particularly the axonal embedded human brain model recently developed by another group²⁹ in which the same material model and embedding technique were implemented. It should be noted that the experimental studies of pig and human brain tissue using similar material testing approaches also reported that the pig brain tissue was softer than human brain tissue.⁴⁰

Simulation of animal experiments

Next, we used the model to simulate the 42 selected pig TBI experiments using their measured rotational velocity time histories as input loading conditions to reproduce the experiments. All simulations were performed in LS-DYNA. The details of the brain geometries, required for geometry scaling, were not available for the animals in this dataset, and therefore mass scaling was used. However, in a recent publication by our group,¹² we examined a separate dataset containing 7 four-week-old and 7 two-month-old pigs, in which the brain geometries were available. Then, we measured the anterior-posterior (AP), lateral (L), and superior-inferior (SI) dimensions of the brain and determined that the geometry variations, which were defined as the coefficients of variation (CVs) of the ratios of these dimensions (L/AP and SI/AP), were <6% across subjects within each age group and both combined. The mean, standard deviation, and CV values for these L/AP and SI/AP are given in Table 1 for each age group and both combined. This analysis suggested that uniform mass scaling can be used for scaling the animals with the age range used in this study.

Table 1.

Summary of Brain Geometry Variations Across 4-Week-Old Piglets, 2-Month-Old Piglets, and Both Ages Combined

Pig brain geometry variations	$\frac{lateral\left(L\right)}{anterior-posterior\left(AP\right)}ratio$		$\frac{superior-inferior\left(SI\right)}{anterior-posterior\left(AP\right)}ratio$
	Mean ± standard deviation	Coefficient of variation (%)	Mean ± standard deviation	Coefficient of variation (%)
4-week-old	0.6763 ± 0.0250	3.71	0.6344 ± 0.0376	5.93
2-month-old	0.6606 ± 0.0172	2.61	0.6125 ± 0.0326	5.33
Combined ages	0.6685 ± 0.0222	3.32	0.6234 ± 0.0359	5.76

The anisotropic pig brain FEM was used as the base for the FE simulations and scaled according to the brain mass of each animal using uniform, isometric mass scaling approach (with scale factor ${\lambda }_x={\lambda }_y={\lambda }_z={\left(m_{scaled}∕m_{base}\right)}^{\frac{1}{3}}$).⁴¹ For each brain element in each simulation, first principal strain at each output state (0.1 ms) was extracted and its maximum value during the entire simulation was calculated as the maximum principal strain (MPS). Similarly, for each axonal fiber element in each simulation, the axial logarithmic strain at each output state was calculated and its maximum value over the simulation time was defined as the maximum axonal strain (MAS). The strain rate for each brain/axonal fiber element was calculated at every 0.1-ms time step as the discrete derivative of the 5-point moving-window-average smoothed strain signal (first principal strain for the brain elements and the axial logarithmic strain for the axonal fiber elements) for each element.

The maximum values of the strain rate over the entire simulation time were defined as maximum principal strain rate (MPSR) for each brain element and MASR for each axonal fiber element. Similarly, the strain times strain rate (SxSR) was calculated as multiplication of strain by its strain rate at each time step, and its maximum value over the entire simulation time was defined as MPSxSR for each brain element or MASxSR for each axonal fiber element.

Finite element model and neuropathology colocalization

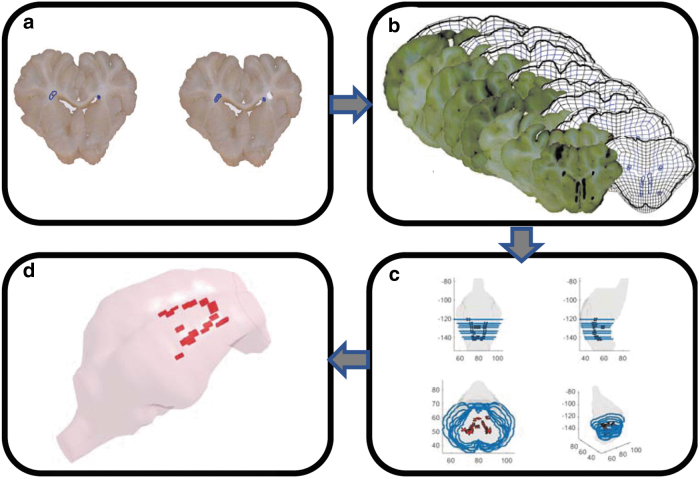
In this step, we registered the neuropathology maps, previously generated for each piglet (details in section on Neuropathology analysis), onto the FEM scaled to the corresponding piglet brain. This step was conducted to find the coordinates of the areas with axonal damage within the 3D geometry of the pig brain FEM. For each animal, the coronal slices of the scaled FEM with a thickness of one brain element (1.0–1.8 mm) were generated and overlayed to the equivalent histopathological maps generated at every ∼3-mm coronal brain tissue slices throughout the whole brain. Criteria, including shape, width, area, and anatomical structures, were considered in order to find the correct location for mapping of histopathological slices onto the FEM slices. A schematic summarizing the workflow of the FEM-neuropathology colocalizaton for 1 animal as an example is shown in Figure 3. TAI areas as shown in Figure 1 had different sizes. In order to standardize the size of TAI areas, each area was partitioned to smaller areas with an almost uniform size of 0.29 ± 0.07 mm² as shown in Figure 3. This area size is close to the value of cross-section area (0.38 mm²) selected for the axonal fiber elements.

FIG. 3.

A schematic workflow for the FEM-neuropathology colocalization process. Color image is available online.

After colocalization of FEM and neuropathology slices and discretization of TAI areas to areas with small, more uniformly area size, the coordinates of the center of each TAI area and its cross-sectional area size were extracted instead of a set of boundary points defining the area of damage. This simplification allowed the use of lower-dimension data structure. For further analysis, we considered each TAI area as a cylinder with 3-mm thickness and the cross-section (0.29 ± 0.07 mm²) that was extracted for that TAI. Then, for each animal, the minimum distance (d) between the location of each brain element centroid and each axonal fiber element centroid of the scaled FEM to any of the TAI cylindrical regions of that animal was calculated. With this definition, for any element whose centroid was within any TAI cylindrical area, d was equal to zero and for any other element d was calculated as the minimum distance between the element centroid to the outer boundary of the closest TAI cylindrical area. All analyses in this step were performed in MATLAB (The MathWorks, Inc.).

The optimal tissue injury threshold and distance to the actual injury areas

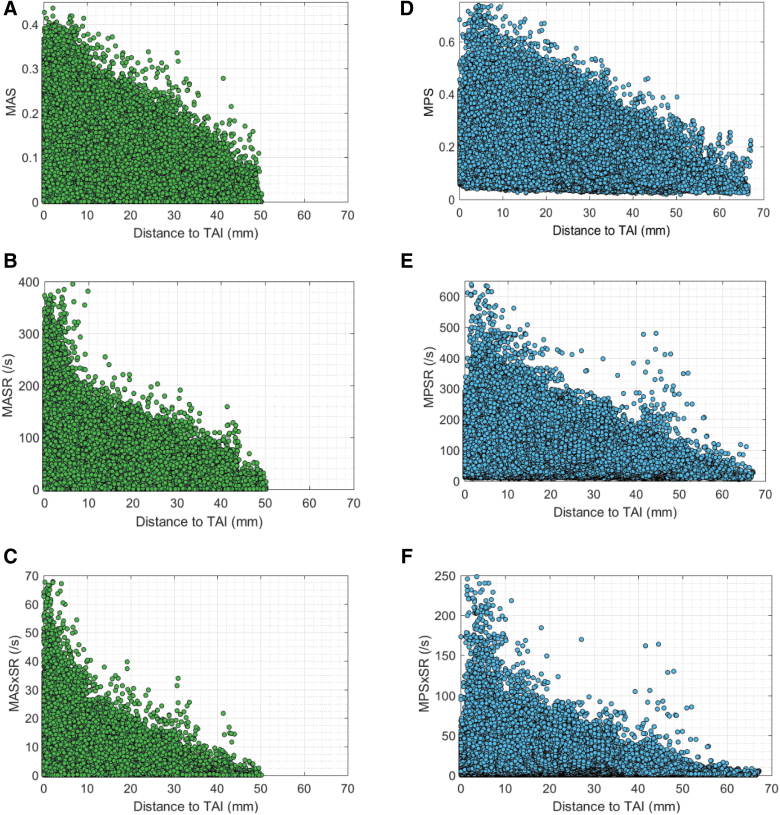
When deformation-related TAI predictor candidates, including MPS, MPSR, MPSxSR, MAS, MASR, and MASxSR, were computed for all animals through FE simulations of the pig TBI experiments and the minimum distance, d, of all FE elements to TAI areas for all animals were calculated (as described in section on Finite element model and neuropathology colocalization), these data were combined and deformation parameters were plotted against “d” for all brain and axonal fiber elements as shown in Figure 4.

FIG. 4.

The brain and axonal fiber deformation parameters including: (A) MAS, (B) MASR, (C) MASxSR, (D) MPS, (E) MPSR, and (F) MPSxSR versus the minimum distance between the location of each brain and axonal fiber element to the regions of TAI identified by histopathology. MAS, maximum axonal strain; MASR, maximum axonal strain rate; MASxSR, maximum product of axonal strain and strain rate; MPS, maximum principal strain; MPSR, maximum principal strain rate; MPSxSR, maximum product of principal strain and strain rate. Color image is availble online.

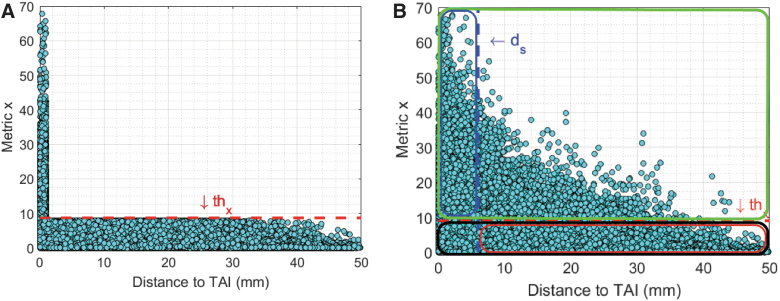
To implement the concept of using FEM for predicting damage at element-by-element approximations, we sought to identify a threshold (th_x) such that any element whose predictor parameter value exceeds that injury threshold as an injured element (predicted as injured; PI) and any element whose predictor value is lower than that injury threshold as a non-injured element (predicted as non-injured; PN). Ideally, all PI elements should be perfectly overlapped (d = 0 mm) with TAI areas identified by histopathology analysis, and all PN elements should be far from (d >> 0 mm) any TAI areas. A schematic representation of an ideal condition is shown in Figure 5A. However, none of the FE-derived predictor candidates fit the ideal characteristics described above. Therefore, instead of looking for a perfect overlap (d = 0), any area within a selected distance (d_s) of any actual TAI can be defined as injured area and any areas with d > d_s can be defined as non-injured area. Given this definition, the PI elements that are within d_s distance (d ≤ d_s) of actual TAI areas can be considered as correctly predicted as injured element (CPI), and the PN elements with d > d_s of actual TAI areas can be determined as correctly predicted as non-injured element (CPN). A schematic representation of CPI and CPN elements for an arbitrary selected th_x and d_s is shown in Figure 5B.

FIG. 5.

(A) Schematic representation of an ideal condition in which all elements whose metric × values exceeding a selected threshold of th_x (dashed red line) are very close to TAIs (d ≈ 0). (B) Schematic representation of predicted injured element (PI; in the green box), correctly predicted injured element (CPI; in the blue box), predicted non-injured elements (PN; in the black box), and correctly predicted non-injured elements (CPN; in the red box) for an arbitrary selected th_x and arbitrary selected distance to actual TAI (d_s). TAI, traumatic axonal injury. Color image is available online.

In order to determine how well the FE-derived predictor candidates can predict TAI spatially, for each of the six TAI predictor candidates (x), we examined a matrix of the threshold values (th_x) and d_s to maximize the average of two optimization criteria: element-based correct prediction rate and TAI detection rate. The overall element-based correct prediction rate was defined as the percentage of the elements that correctly predicted as injured (CPI; x > = th_x and d < = d_s) or non-injured elements (CPN; x < th_x and d > d_s). The element-based true positive prediction rate and true negative prediction rate were defined as CPI/PI and CPN/PN, respectively. The percentage of actual TAI areas that were within distance of d_s from elements predicted as injured (PI; x > = th_x) was defined as TAI detection rate. To calculate the TAI detection rate, the regions within d_s distance of the PI elements for each animal were searched for the actual TAI regions, identified by histopathology analysis. Higher TAI detection rate indicates that more actual TAI regions can be predicted as damaged by the FEM tool using the selected th_x and d_s values. Higher overall element-based correct prediction rate represents better prediction capability of the FE-derived predictor candidate spatially at the element level.

The optimization criterion defined as the average of overall element-based correct prediction rate and TAI detection rate criteria for the selected matrices of th_x and d_s were calculated for all the six FE-derived predictor candidates. To obtain more reliable results, this optimization process was coupled with a k-fold CV technique with k = 5.⁴² Accordingly, for each of the TAI predictor candidates, the data were partitioned into k equal or nearly equal subsamples and at each iteration of k-fold CV, k-1 subsamples were combined and used as a training dataset to determine the optimal injury values (th_x) and d_s, and one subsample was left out as a testing dataset to evaluate the overall element-based correct prediction rate and TAI detection rate performance of the selected th_x and d_s on the new dataset. For each TAI predictor candidate at each iteration of the 5-fold CV, ∼80% of the data were used as training, the th_x and d_s values that resulted in the highest average value of the two criteria, if available, were selected as the optimal combination of injury threshold and distance to actual injury, the determined optimal th_x and d_s values were then examined on the remaining ∼20% testing data set, and the overall element-based correct prediction rate and TAI detection rate on the testing dataset were calculated. The averages of the 5-fold CV results were then calculated and are reported in Table 1.

Results

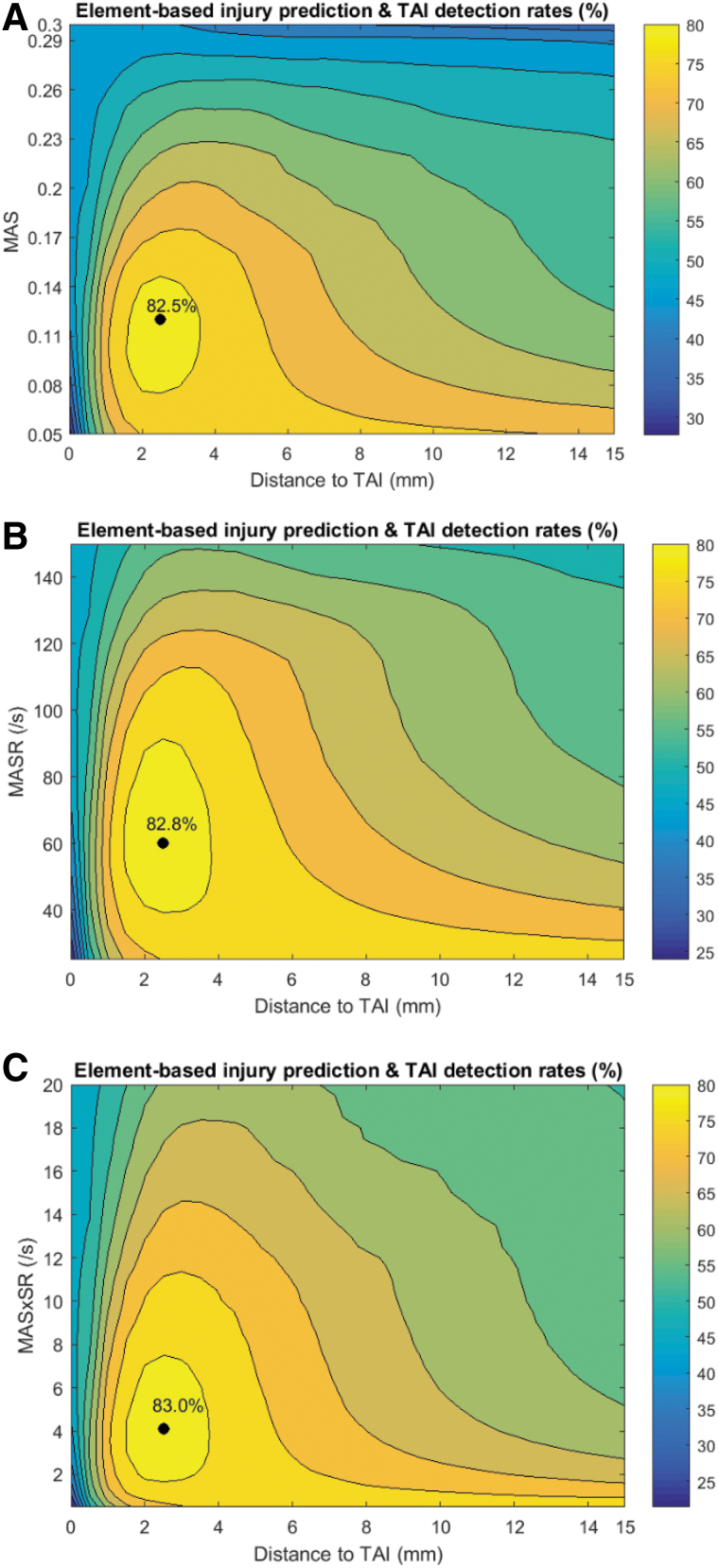
All six selected TAI candidates showed higher values at elements closer and lower values at elements farther from TAI sites (Fig. 4). No optimal d_s and th_x were found for brain tissue metrics MPS, MPSR, and MPSxSR as shown in Supplementary Figure S3. In contrast, all the three axonal deformation-related TAI candidates showed promise for TAI localization. The results of the optimization analysis for these three axonal deformation metrics are given in Table 2. The average of optimal threshold values (and d_s) in 5-fold CV analyses for MAS, MASR, and MASxSR that maximized the optimization criterion (≥82%, shown with black points in Fig. 6 for one of the 5-fold analyses as an example) were 0.118 (2.5 mm), 60 s⁻¹ (2.5 mm), and 4 s⁻¹ (2.5 mm), respectively. These optimal values for MAS, MASR, and MASxSR resulted in 70–73% overall element-based correct TAI prediction rates and 93–95% TAI detection rates.

Table 2.

Summary of the Results of the Optimization Coupled with 5-Fold CV Analyses Including the Results of the Optimal Threshold Values (Highlighted in Bold) and Upper Bound (UB) and Lower Bound (LB) of the Optimal Threshold Ranges

TAI metrics	Threshold (optimal, UB, LB)		On training dataset				On test dataset
		Optimization criterion %	Overall element-based prediction rate %	TAI detection rate %	Element-based true positive rate %	Element-based true negative rate %	Optimization criterion %	Overall element-based prediction rate %	TAI detection rate %	Element-based true positive rate %	Element-based true negative rate %
MAS	0.118 ± 0.005	82.4 ± 0.2	72.2 ± 2.6	93.4 ± 0.7	47.2 ± 0.8	75.4 ± 0.9	82.5 ± 1.2	71.8 ± 3.6	93.1 ± 1.8	47.0 ± 3.1	75.4 ± 3.5
	0.14 ± 0.00	81.0 ± 0.1	72.8 ± 1.7	89.3 ± 0.4	49.1 ± 0.9	75.0 ± 0.9	81.2 ± 1.2	73.2 ± 3.6	89.2 ± 2.5	49.2 ± 3.6	75.1 ± 3.5
	0.08 ± 0.00	80.7 ± 0.7	64.4 ± 0.9	96.2 ± 0.4	42.7 ± 0.9	71.4 ± 1.0	80.7 ± 1.0	65.4 ± 3.4	96.1 ± 1.6	42.5 ± 3.1	71.4 ± 4.1
MASR	60 ± 0	82.8 ± 0.3	73.0 ± 0.7	92.6 ± 1.1	49.5 ± 0.7	76.5 ± 0.9	82.6 ± 2.0	70.5 ± 4.2	94.7 ± 0.6	49.5 ± 3.1	76.5 ± 3.6
	90 ± 0	80.5 ± 0.3	72.8 ± 1.7	87.6 ± 1.2	53.4 ± 0.9	75.1 ± 0.9	79.2 ± 2.8	73.7 ± 3.7	84.7 ± 2.6	53.9 ± 3.9	75.2 ± 3.5
	42.0 ± 2.7	80.3 ± 0.3	64.4 ± 0.9	95.8 ± 1.1	46.2 ± 0.8	73.3 ± 1.0	80.3 ± 2.5	64.4 ± 4.7	96.3 ± 0.5	46.0 ± 3.1	73.2 ± 4.1
MASxSR	4.0 ± 0.0	83.1 ± 0.2	71.5 ± 0.9	94.7 ± 0.57	49.6 ± 0.7	75.8 ± 0.9	83.2 ± 1.2	71.7 ± 3.8	96.1 ± 1.5	49.6 ± 2.6	75.8 ± 3.5
	7.5 ± 0.0	80.2 ± 0.3	73.7 ± 0.8	86.8 ± 1.0	54.1 ± 1.0	74.9 ± 0.9	80.4 ± 1.7	73.9 ± 3.6	86.8 ± 3.6	53.3 ± 3.6	75.0 ± 3.5
	2.0 ± 0.0	80.9 ± 0.5	65.5 ± 0.8	96.2 ± 0.3	45.4 ± 0.8	72.2 ± 1.0	81.2 ± 1.2	66.3 ± 3.9	96.1 ± 1.5	45.2 ± 2.8	72.2 ± 4.1

CV, coefficient of variation; TAI, traumatic axonal injury; MAS, maximum axonal strain; MASR, maximum axonal strain rate; MASxSR, maximum product of axonal strain and strain rate.

FIG. 6.

The average of the two optimization criteria, correct prediction rate and TAI detection rate, for one of the 5-fold analyses as an example, for a matrix of threshold values and ds based on (A) MAS, (B) MASR, and (C) MASxSR metrics. Black dots and yellow contours in each of these plots represent the absolute and range of the optimal threshold values and ds, respectively, for each of these TAI predictor candidates. MAS, maximum axonal strain; MASR, maximum axonal strain rate; MASxSR, maximum product of axonal strain and strain rate; TAI, traumatic axonal injury. Color image is available online.

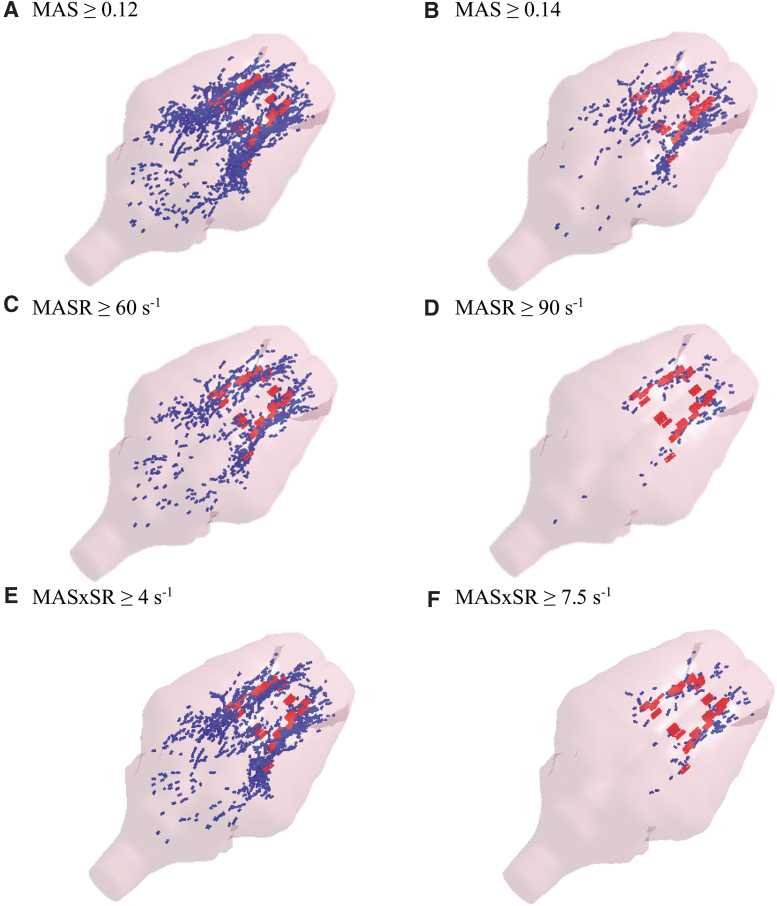
The optimal ranges, defined as threshold values that resulted in a high optimization criterion of ≥80%, were 0.08–0.14, 40–90 s⁻¹, and 2.0–7.5 s⁻¹ for MAS, MASR, and MASxSR, respectively. Elements predicted as injured based on optimal threshold values (0.12, 60 s⁻¹, and 4 s⁻¹) and the high bounds of the optimal threshold ranges (0.14, 90 s⁻¹, and 8 s⁻¹) of the MAS, MASR, and MASxSR metrics for an animal subject as an example are shown in Figure 7. This figure illustrates that a reasonable prediction of the locations of sustained TAI, as evidenced by microscopic histopathology analysis, was obtained. At the optimal thresholds (e.g., MAS = 0.12), which have lower values than the upper threshold bounds (e.g., MAS = 0.14), more elements were past the thresholds and predicted as injured, which resulted in larger blue areas (Fig. 7A,C,E) in comparison to the upper threshold bounds (Fig. 7B,D,F).

FIG. 7.

FEM-predicted sites of TAI (blue areas) using the optimal threshold value (left plots) or the upper bound of the optimal threshold range (right plots) based on (A,B) MAS, (C,D) MASR, and (E,F) MASxSR metrics and TAI areas identified by βAPP histopathology (red areas). βAPP, beta-amyloid precursor protein; FEM, finite element model; MAS, maximum axonal strain; MASR, maximum axonal strain rate; MASxSR, maximum product of axonal strain and strain rate; TAI, traumatic axonal injury. Color image is available online.

This observation was expected and can be explained by the optimization approach that was used in which the threshold values including the optimal and the bounds of the optimal threshold ranges were determined based on the average of two optimization criteria: overall element-based correct prediction rate and TAI detection rate. The optimal thresholds resulted in lower element-based true positive prediction rate and lower element-based overall correct prediction rate or, in other words, overprediction as shown in Figure 7A,C,E by larger FEM predicted injury areas (blue areas) that might not completely overlap with actual measured injury areas (red areas). On the other hand, the upper threshold bounds resulted in a higher overall element-based correct prediction rate and higher element-based true positive prediction rate, which can be observed with close overlap between predicted blue injury areas and actual red injury areas, and a lower detection rate, which increased the chance of missing the detection of actual injury areas.

A good example is the upper bound threshold of MASR (90 s⁻¹; shown in Fig. 7F) in which several actual injured areas in the middle of the brain were not detected by FEM simulations. Therefore, when detection and overall prediction rates are equally important, the optimal thresholds (MAS = 0.12, MASR = 60 s⁻¹, or MASxSR = 4 s⁻¹) are more appropriate to be used, and when the overall prediction rate and true prediction positive rate are more important than the detection rate, and thus less possible overprediction is desirable, the upper bound of the optimal threshold ranges (MAS = 0.14, MASR = 90 s⁻¹, or MASxSR = 7.5 s⁻¹) are suggested to be used. The detection rates using the upper bound of the optimal threshold ranges were lower than the optimal threshold values. For example, as given in Table 2, the detection rate for MAS thresholds of 0.14 and 0.12 are 83.1 ± 1.8 and 89.2 ± 2.5, respectively.

Discussion

In this study, for the first time, we demonstrated that there is spatial correlation between the large brain/axonal deformations obtained from FEM and the actual locations of sustained acute TAI after rapid head rotation. Consistent with our hypothesis, our results showed that the highest FEM-derived brain tissue/axonal fiber deformation parameters, including strain, strain rate, and product of strain and strain rate, were located on/close to the areas where TAI were identified through neuropathology and these deformation parameters were lower farther away from the TAI sites (Fig. 4). Among the six metrics examined herein, the trends of axonal-related metrics, especially MASR and MASxSR, are a more comparable trend to an ideal condition, in which elements with values > threshold are expected to be on/very close (d → 0) to the actual locations of TAI than brain-related metrics.

Using the MAS, MASR, and MASxSR metrics as TAI predictors, we found the optimal prediction distance of 2.5 mm to the actual locations of TAI. All these three metrics are related to the axonal deformations and derived from axonal fiber elements. These results suggest that axonal tract embedded FEM can closely predict the sites of acute TAI. Given the ∼1-mm axonal fiber element length that was used in our FEM and 3-mm thickness increments and 0.586-mm² field size that we used in our TAI histopathology evaluation, this estimation distance is reasonable. Previously, our laboratory attempted to spatially correlate the results of pig brain FEM to the location of TAI using the classical^32,43–45 or white matter tract–oriented isotropic FEM,^3,46 without success, and were limited to predicting the overall absence or presence and volume of TAI.

Therefore, we postulate that this close prediction between the locations of the FE-derived axonal fiber deformations and actual TAIs are attributable to the improvements that were made to the pig FEM herein, including the explicit incorporation of the mesoscopic axonal tract structures and the inclusion of anisotropy into the constitutive model of the brain tissue. Also, it should be noted that although metrics similar to the ones used in the current axonal embedded anisotropic pig brain FEM were used in the previous white matter tract–oriented isotropic pig brain FEMs from our group,^3,46 no spatial correlation was observed between regions of TAI and regions of brain with high tract-oriented MAS, MASR, and MASxSR in those FEMs.^3,46

These results support our postulation that the successful TAI localization obtained herein was mainly attributed to the anisotropic material and modeling approach that we used rather than the FEM-derived metrics used in this study. Our newly developed and validated multi-scale pig FEM is substantially different from the published FEMs in two particular ways. First, the details of the axonal tract structure are now explicitly incorporated into the brain model using the element embedded method.²⁸

This method, in contrast to projecting brain strain responses onto the averaged axonal orientation calculated for each element (e.g., tract-oriented strains), can incorporate the specific axonal tract information by including multiple fiber orientations in each brain element to capture the heterogeneity of orientation and distribution of axonal bundles and the associated axonal-related directional reinforcing https://www.sciencedirect.com/topics/engineering/micromechanical-modellingresponse of the brain tissue throughout the whole brain. With this method, the deformation of each individual axonal bundle throughout the biomechanical loading experienced by the head can be determined. Second, the anisotropic behavior of the brain tissue was modeled by not only embedding the axonal tract pathways into the brain, which automatically reinforce the brain in the direction of axonal bundles, but also tuning the axonal bundle material property based on local FA dispersions using an 8-point scale (details in the Supplementary Appendix and Fig. 2).

In addition, there are some other considerations made in this study that might have contributed to the successful TAI localization obtained herein. For example, our FEM was validated for brain deformation response whereas many (listed in an earlier work⁴⁷), but not all,^3,6,25,28,48 FE head models in the TBI literature have been validated for intracranial pressure response, which may not to be a sufficient validation approach⁴⁸ when a goal of the model is to compare tissue deformation with injury pathology. Moreover, our FE model was validated against in vitro experiments performed using the same system and under similar loading conditions that were used for our TBI experiments. In addition, the center and direction of rotation as well as magnitude of applied kinematics were precisely controlled, measured, and replicated in simulations. These precise kinematic data are not necessarily available for human TBI reconstruction studies. Further, the TAI histopathology was assessed at 6 h post-TBI to minimize the effect of later secondary sequelae that might be caused by hypoxic or ischemic injuries and to more focus on primary injury, which is believed to be caused mainly by the biomechanical loading/deformation.³⁰

The optimal value (and range) of TAI thresholds obtained for the MAS, MASR, and MASxSR metrics were 0.118 (0.80–0.14), 60 s⁻¹ (40–90), and 4 s⁻¹ (2.0–7.5 s⁻¹), respectively. The sites of TAI were determined within a 2.5-mm accuracy distance with 70–73% (and 64–74%) correct overall prediction rates at the element-by-element level using these axonal-deformation optimal values (and ranges) of TAI thresholds. These threshold ranges agree closely with functional thresholds obtained from in vivo, in vitro, and ex vivo studies conducted on isolated axons, axonal and neural cell cultures, and peripheral, spinal, and optic nerve fibers.^49–55 For example, an in vivo stretch study conducted on the spinal nerve found engineering strain thresholds of 0.09–0.16 (equivalent logarithmic strain of 0.086–0.148) for a 50% probability of complete conduction block, resulting in functional axonal injuries.⁴⁹

Another in vivo experimental study on isolated peripheral nerve root⁵⁰ was also shown to hold evidence of a partial conduction block at an engineering strain of 0.12. Another in vivo stretch study of guinea pig optic nerve also reported the optimal receiver operating characteristic Lagrangian strain thresholds of 0.18 and 0.21 (equivalent logarithmic strain of 0.154 and 0.175) for occurrence of electrophysiological impairment and morphological axonal injury by NF68 staining, respectively.⁵¹ The higher strain injury threshold found in the Bain and Meaney⁵¹ study in comparison to ours may be attributed to the NF68 staining for TAI assessment used in that study, which has been shown to be less sensitive³² to axonal damage than βAPP staining used in this study.

Although previous experimental studies found the formation of the axonal/neuronal damage to be dependent on both strain and strain rate,^{49,52,54–59} none of these studies examined a wide range of strain rates with the purpose of determination of threshold values for strain rate (SR) and/or combination of strain and strain rate (SxSR). These studies have shown evidence of axonal damage, such as cell death, conduction block, axonal swelling, bulb formation, and breakage and disintegration of microtubules in axons, which lead to axonal swelling and degeneration at different combinations of strain and strain rate such as strain rate of 50 and 70 s⁻¹ for strain of 0.15 (SxSR = 7.5–10.5), strain rate of ≥30 s⁻¹ for strain of 0.2 (SxSR > = 6),⁵² strain rate of ≥10 s⁻¹ for strain of 0.3 (SxSR ≥3 s⁻¹)⁵⁴ and 0.5 (SxSR ≥5 s⁻¹),⁵⁶ and strain rate of 44 s⁻¹ for strain of ≥0.3 (SxSR ≥13.2 s⁻¹).⁵⁵ The ranges of threshold values that we found in this study are comparable to the range of strain-rate values (SR = 10–70 s⁻¹) and combination of strain and strain-rate values (SxSR = 3.0–13.2 s⁻¹) where axonal damage was observed in the experimental stretch studies.^{49,52,54–57} Also, it should be noted that many in vivo and in vitro studies suggested that the strain threshold for axonal injury is lower at higher strain rates.^49,52,53,58

Future improvements deserve mention. First, an idealized geometry of the pig brain was used in this study and might not capture all the anatomical and geometrical details of the pig brain. In particular, the sulci and gyri anatomical details were not incorporated and thus the effect of these anatomical details on TAI local prediction capability has not been investigated in this study. However, the deformation results of a high-resolution tract-oriented isotropic pig brain FEM recently developed in our laboratory, in which the details of anatomical features such as sulci and gyri were included, did not show spatial correlation with TAI pathology.⁴⁶ In addition, the axonal damage identified through βAPP immunostaining and pathology analysis, as shown in Figure 1, was observed mainly in the deep white matter areas and around the lateral ventricle, and not close to sulci or gyri areas and thus the lack of sulci and gyri might not affect the TAI location prediction results substantially. Second, the brain geometry and axonal tractography were developed based on a single animal whereas the histopathology maps were generated for each animal subject individually. Therefore, although the FEM-histopathology coregistrations were reasonable, they were not perfect.

Future research may use high-resolution subject-specific models to improve the credibility of FEM simulations and FEM-histopathology coregistration analyses. Third, the pig brains were examined for axonal injury at every 3 mm, and TAI areas at each coronal histopathology maps were assumed to be relevant throughout the 3-mm thickness. The 3D spatial resolution of FEM-histopathology coregistration can be increased by finer brain-slice increments in future studies. Finally, the axonal damage was evaluated at 6 h post-TBI in this study. Axonal damage has been shown to evolve over time subsequent to the primary injury, and our data do not capture the possible secondary pathologies that might become apparent later (after 6 h).⁶⁰ However, it should be noted that secondary injuries are shown to be caused by metabolic disturbances, excitotoxicity, and hypoxic or ischemic mechanisms rather than biomechanical mechanisms,³⁰ which is the main focus of the FEM analysis in this article. Therefore, although it was possible to assess TAI at a later time post-TBI, 6 h was selected to reduce the effect of any axonal injury mechanisms other than mechanical causations.

Conclusion

By examining a matrix of different tissue injury threshold values (th_x) and distance to actual TAI sites (d_s) to maximize the overall element-based TAI correct prediction rate and TAI detection rate, defined as the percentage of actual TAI sites ≤d_s from elements ≥th_x, our results showed that three FE-derived metrics related to strain and strain rate of the axonal fiber bundles, including MAS, MASR, and MASxSR, can predict the location of TAI acutely within 2.5 mm with a 93–95% TAI detection rate and 70–73% overall element-based correct prediction rate. Also, the optimal FE-derived tissue injury threshold ranges that we determined in this study agree closely with threshold ranges reported in in vitro and in vivo experimental studies of isolated axonal bundles in the literature. The upper bound of the threshold range lowers the overprediction that usually accompanies with FEM prediction of TBI. We conclude that coupled multi-scale modeling using the element embedding method, which allows axonal bundle tract information to be explicitly incorporated into the macroscale model of brain and the deformation responses along the axonal bundles to be computed at the mesoscopic level, enhance the axonal injury location predictions of the FE tools.

Funding Information

Research reported in this publication was supported by a grant from Football Research, Inc. (FRI) and Biomechanics Consulting and Research, LLC (Biocore) and the National Institutes of Health under award numbers R01NS097549 and R56NS055951. The views expressed are solely those of the authors and do not represent those of any funding sources or their affiliates.

Author Disclosure Statement

No competing financial interests exist.

Supplementary Material

Supplementary Appendix

Supplementary Table S1

Supplementary Figure S1

Supplementary Figure S2

Supplementary Figure S3

Supplementary References