Figure 1:

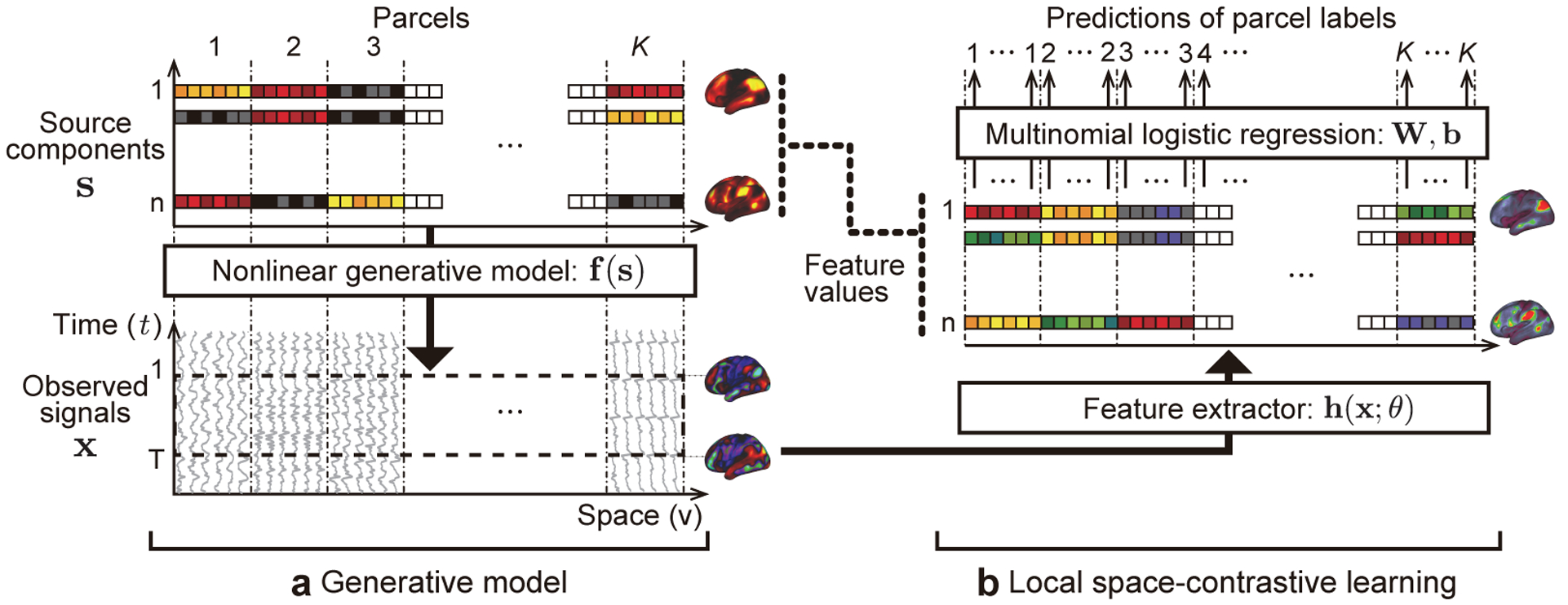
The concept of local space-contrastive learning (LSCL). (a) The generative model is basically a nonlinear version of sICA. The source components are spatial patterns which are spatially (conditionally) mutually independent. The observed time series are given by a nonlinear transformation of the components for each location. Different from ordinary sICA, the components have spatial-parcel-wise stationarity, i.e. different statistics in different parcels, and spatial-parcel-wise independence, which does not necessary mean marginal independence generally assumed in sICA. In addition, LSCL assumes that the components generating the time series can be different for each short temporal window (dotted rectangle on the observed signals), which is in contrast to ordinary sICA, which assumes that the whole time series are generated from the common components. (b) In LSCL, we attempt to find the original components by training a feature extractor to be sensitive to the spatial nonstationarity of the data by using a multinomial logistic regression. The feature extractor is given a short fragment of time series randomly picked from the whole time series at a location as an input, and the logistic regression attempts to predict the parcel label (1, …, K) corresponding to it from the output of the feature extractor (feature values). This framework makes the feature extractor learn component-specific local nonlinear temporal structures, referred to as temporal primitives. See Inline Supplementary Fig. 5 for the detailed procedures to obtain the feature values, which are described in Section 2.5.