Fig. 1. Linear stability of accretion disks.

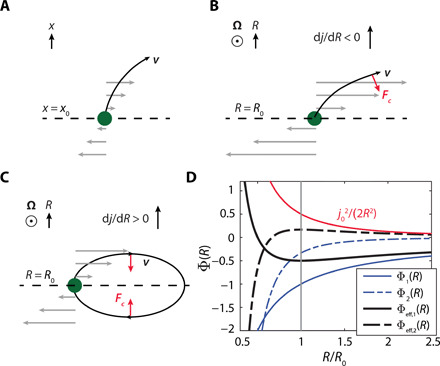
Consider three flows with shears in fluid velocity, v (gray). (A) In a nonrotating flow, small displacements of fluid parcels (green) from initial position x = x₀ lead to unbounded motion (black curved arrow). (B) A rotating flow with angular velocity Ω(R) for radius R in which the specific angular momentum j = ΩR² decreases with R forms a strong shear such that despite the restorative influence of the Coriolis force F_c= −2Ω×v (red arrow), the motion is unbounded. (C) In a rotating Keplerian flow, dj(R)/dR > 0, leading to reduced shear compared to that of (B). As a result, the Coriolis force confines the motion into epicyclic trajectories (black loop). (D) Stability of a parcel on a circular orbit around R = R₀ (gray line) over two disk potentials Φ₁(R) [corresponding to (B)] and Φ₂(R) [corresponding to (C)], where $j_i(R)=\sqrt{R^3\mathrm{d}{\mathrm{\Phi }}_i/\mathrm{d}R}$ (for i = 1, 2) increases with R for Φ₁ (as for a point mass potential) and decreases with R for Φ₂ (here more steeply than for a point mass). We have set j₁(R₀) = j₂(R₀) ≡ j₀. Φ_eff,1 has a minimum at R = R₀ (motion is stable), whereas Φ_eff,2 has a maximum at R = R₀ (motion is unstable). (A) and (C) after (17).