Integration of imaging (epi)genomics data for the study of schizophrenia using group sparse joint nonnegative matrix factorization

Abstract

Schizophrenia (SZ) is a complex disease. Single nucleotide polymorphism (SNP), brain activity measured by functional magnetic resonance imaging (fMRI) and DNA methylation are all important biomarkers that can be used for the study of SZ. To our knowledge, there has been little effort to combine these three datasets together. In this study, we propose a group sparse joint nonnegative matrix factorization (GSJNMF) model to integrate SNP, fMRI and DNA methylation for the identification of multi-dimensional modules associated with SZ, which can be used to study regulatory mechanisms underlying SZ at multiple levels. The proposed GSJNMF model projects multiple types of data onto a common feature space, in which heterogeneous variables with large coefficients on the same projected bases are used to identify multi-dimensional modules. We also incorporate group structure information available from each dataset. The genomic factors in such modules have significant correlations or functional associations with several brain activities. At the end, we have applied the method to the analysis of real data collected from the Mind Clinical Imaging Consortium (MCIC) for the study of SZ and identified significant biomarkers. These biomarkers were further used to discover genes and corresponding brain regions, which were confirmed to be significantly associated with SZ.

I. Introduction

Schizophrenia (SZ) is a complex mental disorder which affects the way one thinks, feels and acts. It has been widely accepted that both genetic and environmental factors play an important role in the causes of SZ. The disorder tends to inherit in a family. In recent years, many studies have been conducted on exploring critical genes associated with SZ and many genetic variants have been identified, for example, the G72/G30 gene locus on chromosome 13q [1], copy number variations on gene GRIK3, EFNA5, AKAP5 and CACNG2 [2], [3] and gene DISC1 variation [4]. In addition, DNA methylation, one of the main epigenetic markers to regulate gene expression, has also been determined to be involved with the development of SZ. Davies et al. showed that the interindividual variations of DNA methylation are significantly correlated between the blood and the brain. Some studies have used blood DNA methylation to identify potential biomarkers for SZ [5], [6]. On the other hand, fMRI has been used to measure brain activity and to identify functional abnormalities within brain regions in SZ [7], [8]. These different datasets (e.g., SNP, fMRI and DNA methylation) represent the same biological sample from different views and provide partial while complementary information; their joint analysis has the potential to reveal the mechanism underlying SZ. Since these imaging and genomic data have different scales and formats, they cannot be simply aggregated for joint analysis. Most of existing works either use single dataset [9], [10], [11] or two datasets [12] and only a few studies [13], [14] exist that can take advantage of three or more datasets for a more comprehensive analysis of SZ.

Canonical correlation analysis (CCA) [15] and partial least squares (PLS) [16] are two popular methods for exploring the relationships between two data sets. The CCA (PLS) method maximizes the correlation (covariance) between the linear combinations of variables from two datasets to find the correlated components. To overcome the small sample size but large dimension of feature problem in imaging (epi)genomics, sparse CCA [17], sparse PLS [18] and sparse reduced rank regression [19] have been proposed by using sparse constraint in the model. To incorporate biological knowledge and group structures (e.g., SNPs within a gene, voxels within a region, and methylation sites within a gene), group sparse CCA [12] and network-regularized PLS [20] model were proposed. However, the above models were for the analysis of pairwise datasets and cannot handle three or more datasets. D.M. Witten et al. [21] proposed a sparse multiple CCA (SMCCA) model, which is an extension of two-way sparse CCA model when three or more datasets are considered for correlation analysis. In our recent work et al. [22] we proposed an adaptive SMCCA model to adaptively adjust the weight coefficients on the pairwise covariances in the SMCCA model. Despite of these efforts, there has been limited work to combine three or multiple imaging genomics data sets.

Nonnegative matrix factorization (NMF) [23] has been proposed to represent objects by incorporating the nonnegativity constraints, i.e., factorizing the representation matrix into two nonnegative ones. Specifically, it represents data as a linear combination of a set of nonnegative basis vectors. The nonnegativity constraints facilitate the interpretation of discovered latent factors, and many variants of NMF have been developed such as sparse NMF [24], [25], group sparse NMF (GSNMF) [26] and graph regularized NMF [27]. These methods incorporate both prior knowledge and specific data structure (e.g., sparsity, group and graph constrains). Zhang et al. [28] proposed a joint nonnegative matrix factorization (JNMF) framework, which simultaneously factorizes multiple data matrices to reveal hidden associations for pattern discovery in cancer genomic data. In JNMF framework, multiple data matrices were projected into a common subspace (i.e., the same set of basis vectors) to explore the correlation among multiple datasets. Since the correlated component pairs correspond to the same basis vectors, it is different from CCA-based or PLS-based model.

In [29], we have employed the JNMF model to extract correlative modules from SNP, fMRI and methylation for the SZ study. However, we haven’t taken into account specific group structures in the data. In our preliminary work [30], we proposed a group sparse joint nonnegative matrix factorization (GSJNMF) model for multiple data integration. In current paper, we present the detailed procedure for the solution of the model and the convergence analysis. We also propose a parameter selection strategy based on variable stability selection for the stability of the results. Then we employ the GSJNMF model to identify correlative modules associated with SZ. Based on the modules, we can identify significant genes or biomarkers associated with SZ.

The rest of the paper is organized as follows. In Section II, we briefly review NMF and its variants. In Section III we describe the proposed GSJNMF model and the numerical algorithm for its solution. We then present the experimental results on both simulation and real SZ datasets in Section IV. We conclude the paper in Section V by summarizing the major contributions of the work.

II. Related work

In this section, we will briefly review NMF and some of its variants.

A. NMF

NMF [23] is a matrix factorization algorithm with many applications. Given m samples in ${ℝ}^n$, whose elements are all nonnegative and arranged in columns of a nonnegative matrix $X\in {ℝ}_{+}^{m\times n}$, NMF aims to find its approximation with two low-rank nonnegative matrices $W\in {ℝ}_{+}^{m\times r}$ and $H\in {ℝ}_{+}^{r\times n}$, with r < min(m, n). It can be formulated as

$$\underset{W,H}{\min }\Vert X-WH{\Vert }_F^2\text{s.t.}W,H\ge 0,$$ (1)

where $\Vert \cdot {\Vert }_F$ is the Frobenius norm, $W\in {ℝ}_{+}^{m\times r}$ stores the basis column vectors and $H\in {ℝ}_{+}^{r\times n}$ stores the corresponding column coefficient vectors. r is the number of the basis vectors.

The objective function of NMF in Eq. (1) is nonconvex with respect to W and H, so it is impractical to find the global minimizer. Fortunately, it is convex in either W or H only, so an iterative optimization can be used to find a local minimizer. Lee et al. [31] developed the multiplicative update algorithm to solve the optimization problem in Eq. (1) as follows

$$W_{ik}\leftarrow W_{ik}\frac{{\left(X{H}^T\right)}_{ik}}{{\left(WH{H}^T\right)}_{ik}},H_{jk}\leftarrow H_{jk}\frac{{\left(W^{T}X\right)}_{jk}}{{\left(W^{T}WH\right)}_{jk}}.$$ (2)

For each column X_·j, a linear, nonnegative combination of the basis vectors is given by

$$X_{.j}=\sum _{i=1}^r{W}_{.i}{H}_{ij}=W{H}_{.j},$$ (3)

where W_·i is the i-th column vector of W. Thus, the r basis vector W_·i can be considered as the skeleton of the data, while the r-dimensional coefficient vector H_·j gives the weights of each basis vectors on X_·j. The basis vectors can often discover data structures that are latent in the X.

B. Variants of NMF

With the nonnegativity constraint, NMF can learn a parts-based representation of a dataset. However, NMF sometimes fails to discover intrinsic structures of the data, which is essential to the real-world applications. By incorporating prior information about the dataset or enforcing a sparsity constraint, we can further improve the model or make the results more interpretable.

For a nonnegative data matrix X ≥ 0, Hoyer proposed nonnegative sparse coding (NSC) model [24] to ensure sparsity of the encoding matrix as follows

$$\underset{W,H}{\min }\frac{1}{2}\Vert X-WH{\Vert }_F^2+\lambda \sum _{ij}{H}_{ij}\text{s.t.}W,H\ge 0,$$ (4)

where λ > 0 is a parameter for balancing the two terms.

In Eq. (4), since H ≥ 0, we can get

$$\sum _{ij}{H}_{ij}=\sum _{ij}\left|H_{ij}\right|=\Vert \mathrm{vec}(H){\Vert }_1,$$ (5)

which is the sparse constraint. vec(·) is a vectorization operator. In [25], Hoyer proposed a novel sparseness measure based on the relationship between the L₁ norm and L₂ norm. Given a vector $x\in {ℝ}^n$

$$\text{sparseness}(x)=\frac{\sqrt{n}-\Vert x{\Vert }_1/\Vert x{\Vert }_2}{\sqrt{n}-1}.$$ (6)

This function equals to 1 if and only if x contains only a single non-zero element, and equals to 0 if and only if all elements are equal (up to signs), a trade-off between the two extremes. Hoyer [25] enforced this sparse constraint to the columns of W and rows of H with desired sparseness values as follows

$$\begin{gathered} \text{sparseness}\left(W_{.i}\right)=S_w,\forall i,i=1,\dots ,r, \\ \text{sparseness}\left(H_{i.}\right)=S_h,\forall i,i=1,\dots ,r, \end{gathered}$$ (7)

where S_w and S_h are predefined.

Liu et al. [26] proposed a group sparse NMF (GSNMF) model to learn multiple linear manifolds for face recognition. GSNMF imposes the group sparsity constraint on the column vectors of the coefficient matrix to get a group sparse representation. For nonnegative coefficient matrix $H\in {ℝ}_{+}^{r\times n}$, let’s assume there are K manifolds and the dimension of each manifold is p. For each row vector of H, it can be divided into K groups and each group has p coefficients. The i-th row, k-th group norm ${\Vert H_{i\cdot }\Vert }_{{\mathcal{G}}_k}$ is defined as

$${\Vert H_{i.}\Vert }_{{\mathcal{G}}_k}={\left(\sum _{\alpha \in {\mathcal{G}}_k}{H}_{i\alpha }^2\right)}^{\frac{1}{2}},$$ (8)

where ${\mathcal{G}}_k$ is the column index set of the k-th group and i is the row index. Then the group sparsity for H is defined by

$$\Vert H{\Vert }_{\mathcal{G}}=\sum _{i,k}{\Vert H_{i.}\Vert }_{{\mathcal{G}}_k}=\sum _{i,k}{\left(\sum _{\alpha \in {\mathcal{G}}_k}{H}_{i\alpha }^2\right)}^{\frac{1}{2}}.$$ (9)

If we consider each row as a group, $\Vert \cdot {\Vert }_{\mathcal{G}}=\Vert \cdot {\Vert }_{2,1}$.

All the variants of NMF model described above just factorize one single matrix and cannot handle multiple data matrices. Zhang et al. [28] proposed a joint NMF (JNMF) framework, which simultaneously projects multiple types of data matrices onto a common subspace. The common subspace is spanned by nonnegative basis vectors, which can be used to represent the heterogeneous variables with nonnegative weights. Based on the nonnegative weights on a particular basis vector, JNMF can identify the correlated variables and reveal the hidden associations. Given three nonnegative matrices $X_1\in {ℝ}_{+}^{m\times n_1}$, $X_2\in {ℝ}_{+}^{m\times n_2}$, $X_3\in {ℝ}_{+}^{m\times n_3}$, the JNMF model is formulated as follows

$$\begin{gathered} \underset{{}_{W,H_1,H_2,H_3}}{\min }\sum _{q=1}^3{\Vert X_q-W{H}_q\Vert }_F^2 \\ \text{s.t.}W,H_1,H_2,H_3\ge 0, \end{gathered}$$ (10)

where $W\in {ℝ}_{+}^{m\times r}$ stores the common basis vectors shared by the three data matrices and $H_q\in {ℝ}_{+}^{r\times n_q},(q=1,2,3)$ are the corresponding coefficient vectors.

III. Proposed method

The nonnegative constraint in NMF model only allows additive combinations of the nonnegative basis vectors, which differs from other matrix factorization methods such as singular value decomposition (SVD). As a result, NMF can learn parts-based representation, which find good applications to many real-world problems such as document clustering [32] and DNA gene expression analysis [33]. JNMF simultaneously projects multiple data matrices into a common subspace to explore their correlations but overlook the prior knowledge or specific structure information in the data. In this section, we propose the group sparse JNMF (GSJNMF) model by enforcing group sparse constraint.

A. GSJNMF

We consider three types of datasets from the same samples. After preprocessing, we make the data matrices nonnegative and denote them as $X_1\in {ℝ}_{+}^{m\times n_1}$, $X_2\in {ℝ}_{+}^{m\times n_2}$, and $X_3\in {ℝ}_{+}^{m\times n_3}$, where m is the sample size and n_i is the number of variables in data X_i. For data X_i (i = 1, 2, 3), assuming there are K_i disjoint groups in the n_i variables, we denote the group information of variables in X_i as

$$\begin{gathered} {\mathcal{G}}^i=\left\{{\mathcal{G}}_1^i,{\mathcal{G}}_2^i,\cdots ,{\mathcal{G}}_{K_i}^i\right\} \\ \text{s.t.}{\mathcal{G}}_p^i\cap {\mathcal{G}}_q^i=\varnothing ,p\ne q \\ \underset{j=1}{\overset{K_i}{\cup }}{\mathcal{G}}_j^i=\left\{1,2,\cdots ,n_i\right\}, \end{gathered}$$ (11)

where ${\mathcal{G}}_j^i$ is the column index set of the j-th group in data X_i. The GSJNMF model is then formulated as

$$\begin{gathered} \underset{{}_{W,H_1,H_2,H_3}}{\min }\mathcal{F}=\sum _{i=1}^3\left(\frac{1}{2}{\Vert X_i-W{H}_i\Vert }_F^2+{\lambda }_i{\Vert H_i\Vert }_{{\mathcal{G}}^i}\right), \\ \text{s.t.}W,H_1,H_2,H_3\ge 0, \\ {\Vert W_{.j}\Vert }_2^2=1(j=1,\cdots ,r), \end{gathered}$$ (12)

where $W\in {ℝ}_{+}^{m\times r}$, $H_1\in {ℝ}_{+}^{r\times n_1}$, $H_2\in {ℝ}_{+}^{r\times n_2}$, $H_3\in {ℝ}_{+}^{r\times n_3}$. r is a predefined rank and λ₁, λ₂, λ₃ are regularization parameters. W_.j is the j-th column basis vector in matrix W. ${\Vert H_i\Vert }_{{\mathcal{G}}^i}$ is the group sparse penalty term of matrix H_i defined as follows

$${\Vert H_i\Vert }_{{\mathcal{G}}^i}=\sum _{j,k}{\left(\left|{\mathcal{G}}_k^i\right|\sum _{\alpha \in {\mathcal{G}}_k^i}{\left(H_i\right)}_{j\alpha }^2\right)}^{\frac{1}{2}},$$ (13)

where $\left|{\mathcal{G}}_k^i\right|$ is the number of elements in ${\mathcal{G}}_k^i$.

GSJNMF simultaneously factorizes multiple data matrices and obtains the shared basis vectors. Since the variables in each data matrix have group structure, the group sparse penalty on the coefficient vectors can yield simultaneously nonzero weights within the same group. The constraint on the basis vectors W is used to prevent the elements in W from growing arbitrarily large. In particular, the term $\left|{\mathcal{G}}_k^i\right|$ in (13) can reduce the effect of group size difference during the process of optimizing the coefficient values.

B. Multiplicative updating algorithm

The objective function of GSNMF in Eq. (12) is nonconvex in W, H₁, H₂, H₃. Therefore, it is difficult for an algorithm to find the global minimizer. In the following, we introduce an iterative algorithm to find a local minimizer. Let $\mathrm{\Psi }\in {ℝ}^{m\times r}$, ${\mathrm{\Phi }}_1\in {ℝ}^{r\times n_1}$, ${\mathrm{\Phi }}_2\in {ℝ}^{r\times n_2}$, ${\mathrm{\Phi }}_3\in {ℝ}^{r\times n_3}$ be the Lagrange multipliers for constraint W ≥ 0, H₁ ≥ 0, H₂ ≥ 0, H₃ ≥ 0, respectively; the Lagrange function is then given by

$$\begin{gathered} \mathcal{L}=\sum _{i=1}^3\left(\frac{1}{2}{\Vert X_i-W{H}_i\Vert }_F^2+{\lambda }_i{\Vert H_i\Vert }_{{\mathcal{G}}^i}\right) \\ +\sum _{i=1}^3\mathrm{tr}\left({\mathrm{\Phi }}_i{H}_i^T\right)+\mathrm{tr}\left(\mathrm{\Psi }{W}^T\right), \end{gathered}$$ (14)

where tr(·) is the trace of a matrix. The partial derivatives of $\mathcal{L}$ with respect to W and H_i (i = 1, 2, 3) are

$$\frac{\partial \mathcal{L}}{\partial W}=\sum _{i=1}^3\left(\left(W{H}_i-X_i\right)H_i^T\right)+\mathrm{\Psi },$$ (15)

$$\frac{\partial \mathcal{L}}{\partial H_i}=W^T\left(W{H}_i-X_i\right)+{\lambda }_i\frac{\partial {\Vert H_i\Vert }_{{\mathcal{G}}^i}}{\partial H_i}+{\mathrm{\Phi }}_i.$$ (16)

Based on the Karush-Kuhn-Tucker conditions Ψ_jkW_jk = 0, or specifically (Φ_i)_jk(H_i)_jk = 0, we can get the following equations for W_jk and (H_i)_jk:

$$\begin{gathered} \sum _{i=1}^3{\left(W{H}_i{H}_i^T\right)}_{jk}{W}_{jk}=\sum _{i=1}^3{\left(X_i{H}_i^T\right)}_{jk}{W}_{jk}, \\ {\left(W^{T}W{H}_i+{\lambda }_i\frac{\partial {\Vert H_i\Vert }_{{\mathcal{G}}^i}}{\partial H_i}\right)}_{jk}{\left(H_i\right)}_{jk}={\left(W^T{X}_i\right)}_{jk}{\left(H_i\right)}_{jk}. \end{gathered}$$

Then we can get the following multiplicative updating rules:

$$W_{jk}\leftarrow W_{jk}\frac{{\sum }_{i=1}^3{\left(X_i{H}_i^T\right)}_{jk}}{{\sum }_{i=1}^3{\left(W{H}_i{H}_i^T\right)}_{jk}},$$ (17)

$${\left(H_i\right)}_{jk}\leftarrow {\left(H_i\right)}_{jk}\frac{{\left(W^T{X}_i\right)}_{jk}}{{\left(W^{T}W{H}_i+{\lambda }_i\frac{\partial {\Vert H_i\Vert }_{{\mathcal{G}}^i}}{\partial H_i}\right)}_{jk}},$$ (18)

where

$${\left(\frac{\partial {\Vert H_i\Vert }_{{\mathcal{G}}^i}}{\partial H_i}\right)}_{jk}=\frac{\sqrt{\left|{\mathcal{G}}_q^i\right|}{\left(H_i\right)}_{jk}}{\sqrt{{\sum }_{\alpha \in {\mathcal{G}}_q^i}{\left(H_i\right)}_{j\alpha }^2}}.$$ (19)

The iteration will terminate when the relative error of the value of the objective function in Eq. (12) between two iterations is smaller than a predefined tolerance τ > 0. We summarize the algorithm to solve GSJNMF model in Algorithm 1. Since the objective function (12) is nonconvex on W, H₁, H₂, H₃ as a whole, the above algorithm may only find a local minimizer. We repeat the procedure for 100 times with different initialization settings. The solution with the lowest objective function value was used as the final result for further analysis.

C. Convergence analysis

From Eq. (12), we can know that the objective function $\mathcal{F}$ is bounded from below by zero. If we can prove that the $\mathcal{F}$ is nonincreasing under the multiplicative update rule given in Eq. (17) and Eq. (18), the objective function $\mathcal{F}$ will be invariant if and only if W and H_i (i = 1, 2, 3) are at a stationary point. The final solution will be a local minimizer. To simplify the proof, we just prove that $\mathcal{F}$ is nonincreasing under the update rule for H_i (i = 1,2,3). The proof for $\mathcal{F}$ being nonincreasing under the update rule for W can follow a similar way. We introduce an auxiliary function to prove the convergence as Lee et al. used in [31] and the definition of the auxiliary function is given in the following.

Definition 1: G(h, h^∗) is an auxiliary function for F(h) if the condition G(h, h^∗) ≥ F(h), G(h, h) = F(h) is satisfied.

Algorithm 1.

The algorithm to solve GSJNMF model

Input: $X_i\in {ℝ}_{+}^{m\times n_i}$, ${\mathcal{G}}^i$, λi, (i = 1, 2, 3), r, τ.

Initialize W and Hi, (i = 1, 2, 3) to random positive matrices.

k = 1.

while 1 do

Calculate the current function value fk on Eq. (12).

update W by using Eq. (17).

for j = 1 : r

W.j = W.j/||W.j||2.

end for

Update Hi (i = 1, 2, 3) by using Eq. (18).

Calculate the current function value fk+1 on Eq. (12).

if |(fk − fk+1)/fk+1| < τ

break.

end if

k = k + 1.

end while

Output: W, Hi, (i = 1, 2, 3).

For H_i, considering any element (H_i)_jk, we use Fi_jk to denote the part of $\mathcal{F}$ which is only relevant to (H_i)_jk. The first order and second order derivative of Fi_jk are given as

$$\begin{gathered} F{i}_{jk}^{\prime }={\left(W^T\left(W{H}_i-X_i\right)\right)}_{jk}+{\lambda }_i{\left(\frac{\partial {\Vert H_i\Vert }_{{\mathcal{G}}^i}}{\partial H_i}\right)}_{jk}, \\ F{i}_{jk}^{\prime \prime }={\left(W^{T}W\right)}_{jj}+{\lambda }_i{\left(\frac{{\partial }^2{\Vert H_i\Vert }_{{\mathcal{G}}^i}}{{\partial }^2{H}_i}\right)}_{jk}. \end{gathered}$$

Lemma 1: Function

$$\begin{gathered} G(h,{(H_i^{(t)})}_{jk}) \\ =F{i}_{jk}({(H_i^{(t)})}_{jk})+F{i}_{jk}^{\prime }({(H_i^{(t)})}_{jk})(h-{(H_i^{(t)})}_{jk}) \\ +\frac{{(W^{T}W{H}_i^{(t)})}_{jk}+{\lambda }_i{\left(\frac{\partial {\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{\partial H_i^{(t)}}\right)}_{jk}}{2{(H_i^{(t)})}_{jk}}{(h-{(H_i^{(t)})}_{jk})}^2 \end{gathered}$$ (20)

is an auxiliary function for Fi_jk.

Proof: Obviously, G(h, h) = Fi_jk(h), we only need to prove $G(h,{(H_i^{(t)})}_{jk})\ge F{i}_{jk}(h)$. The Taylor series expansion of Fi_jk(h) in ${(H_i^{(t)})}_{jk}$ is given as

$$\begin{gathered} F{i}_{jk}(h) \\ =F{i}_{jk}({(H_i^{(t)})}_{jk})+F{i}_{jk}^{\prime }({(H_i^{(t)})}_{jk})(h-{(H_i^{(t)})}_{jk}) \\ +\frac{F{i}_{jk}^{\prime \prime }({(H_i^{(t)})}_{jk})}{2}{(h-{(H_i^{(t)})}_{jk})}^2. \end{gathered}$$ (21)

Comparing Eq. (20) with Eq. (21), we can find that $G(h,{(H_i^{(t)})}_{jk})\ge F{i}_{jk}(h)$ is equivalent to

$$\begin{gathered} {(W^{T}W{H}_i^{(t)})}_{jk}+{\lambda }_i{\left(\frac{\partial {\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{\partial H_i^{(t)}}\right)}_{jk} \\ \ge \left({\left(W^{T}W\right)}_{jj}+{\lambda }_i{\left(\frac{{\partial }^2{\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{{\partial }^2{H}_i^{(t)}}\right)}_{jk}\right){(H_i^{(t)})}_{jk}. \end{gathered}$$ (22)

Obviously, we have

$$\begin{gathered} {\left(W^{T}W{H}_i^{(t)}\right)}_{jk} \\ =\sum _v{\left(W^{T}W\right)}_{jv}{\left(H_i^{(t)}\right)}_{vk}\ge {\left(W^{T}W\right)}_{jj}{\left(H_i^{(t)}\right)}_{jk}. \end{gathered}$$ (23)

From Eq. (19), we have

$${\left(\frac{\partial {\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{\partial H_i^{(t)}}\right)}_{jk}=\frac{\sqrt{\left|{\mathcal{G}}_q^i\right|}{\left(H_i^{(t)}\right)}_{jk}}{\sqrt{{\sum }_{\alpha \in {\mathcal{G}}_q^i}{\left(H_i^{(t)}\right)}_{j\alpha }^2}}.$$ (24)

We can also get

$$\begin{gathered} {\lambda }_i{\left(\frac{{\partial }^2{\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{{\partial }^2{H}_i^{(t)}}\right)}_{jk}{\left(H_i^{(t)}\right)}_{jk} \\ ={\lambda }_i{\left(\frac{\partial {\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{\partial H_i^{(t)}}\right)}_{jk}\left(1-\frac{{\left(H_i^{(t)}\right)}_{jk}^2}{{\sum }_{\alpha \in {\mathcal{G}}_q^i}{\left(H_i^{(t)}\right)}_{j\alpha }^2}\right) \\ \le {\lambda }_i{\left(\frac{\partial {\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{\partial H_i^{(t)}}\right)}_{jk}. \end{gathered}$$ (25)

Adding Eq. (23) and Eq. (25), we can get Eq. (22). Thus $G(h,{(H_i^{(t)})}_{jk})\ge F{i}_{jk}(h)$ holds and function $G(h,{(H_i^{(t)})}_{jk})$ is an auxiliary function for $F{i}_{jk}$. ∎

Lemma 2: If G is an auxiliary function of F, then F is nonincreasing under the update h^(t+1) = arg min G(h, h^(t)).

Proof:

$$\begin{gathered} G\left(h^{(t+1)},h^{(t+1)}\right)=F\left(h^{(t+1)}\right) \\ \le G\left(h^{(t+1)},h^{(t)}\right)\le G\left(h^{(t)},h^{(t)}\right)=F\left(h^{(t)}\right), \end{gathered}$$

then F(h^(t+1)) ≤ F(h^(t)). So F is nonincreasing under the update h^(t+1) = arg min G(h, h^(t)). ∎

Based on Lemma 2, we only show that the multiplicative updating rules given in Eq. (18) is the optimum of $G(h,{(H_i^{(t)})}_{jk})$.

$$\begin{gathered} \frac{\partial G(h,{(H_i^{(t)})}_{jk})}{\partial h} \\ =\frac{{\left(W^{T}W{H}_i^{(t)}\right)}_{jk}+{\lambda }_i{\left(\frac{\partial {\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{\partial H_i^{(t)}}\right)}_{jk}}{{\left(H_i^{(t)}\right)}_{jk}}(h-{(H_i^{(t)})}_{jk}) \\ +{\left(W^T\left(W{H}_i-X_i\right)\right)}_{jk}+{\lambda }_i{\left(\frac{\partial {\Vert H_i\Vert }_{{\mathcal{G}}^i}}{\partial H_i}\right)}_{jk}=0. \end{gathered}$$ (26)

Then we can get

$$h={\left(H_i^{(t)}\right)}_{jk}\frac{{\left(W^T{X}_i\right)}_{jk}}{{\left(W^{T}W{H}_i^{(t)}+{\lambda }_i\frac{\partial {\Vert H_i^{(t)}\Vert }_{{\mathcal{G}}^i}}{\partial H_i^{(t)}}\right)}_{jk}},$$ (27)

which is the updating rule of H_i given in Eq. (18). Due to the property of the auxiliary function, Fi_jk is nonincreasing under this updating rule.

D. Identification of modules

After GSJNMF, the three datasets were projected onto a common subspace whose basis vectors were stored in the basis matrix W. The basis vectors can be considered as the skeleton of the three datasets. For j-th basis vector, we can select the variables in X_q with large coefficients in j-th row of H_q to form a membership variable set $S_j^q,(j=1,2,\cdots ,r;q=1,2,3)$. Since $S_j^1$, $S_j^2$ and $S_j^3$ all have large coefficients on the j-th basis vector in the common subspace, the j-th basis vector is the bridge that link the three member variable sets. In other words, each basis vector can define a module and the member variables across the three datasets in the module are correlated. For example, $S_j=\{S_j^1,S_j^2,S_j^3\}$ is a module corresponding to the j-th basis vector. In [33], researchers have used the maximum of each column of coefficient matrix to determine the variable’s membership. In this way, each variable can belong to only one module. However, some variables may be either inactive in any module or active in multiple modules.

Considering above facts, we calculated the z-score [28] for each element in each row of coefficient matrices H_q (q=1, 2, 3) by

$$z_{ij}=\frac{x_{ij}-{\mu }_i}{{\sigma }_i}$$ (28)

where μ_i is the mean value of i-th row vector in H_q and σ_i is the standard deviation. For H_q, z_ij > T means that the j-th variable in dataset X_q is a member of $S_i^q,q=1,2,3$ and T > 0 is a given threshold. Since GSJNMF extract the correlated variables from multiple datasets based on the shared basis vectors from the same sample, this model can only be used for multiple datasets from the same subject.

E. Significance estimation

For module S = {S¹, S², S³}, we expect that the variables in S¹, S² and S³ are correlated. To check if such relationship is statistically significant, we employ a permutation test to estimate the P-value of the identified modules. Assuming the number of elements in S¹, S² and S³ are l₁, l₂ and l₃, respectively, we then denote them by $A=\left[a_1,a_2,\cdots ,a_{l_1}\right],B=\left[b_1,b_2,\cdots ,b_{l_2}\right],C=\left[c_1,c_2,\cdots ,c_{l_3}\right]$, where a_i, b_j, c_k are column vectors from X₁, X₂, X₃, respectively, and the length of the vector is the number of samples. We use ρ(x, y) to represent the Pearson correlation between x and y. Based on the above assumption, the mean correlation among the three datasets in a module can be given by

$$\begin{gathered} {\rho }^{*}=\frac{1}{3}(\frac{1}{l_1{l}_2}\sum _{i=1}^{l_1}\sum _{j=1}^{l_2}\left|\rho \left(a_i,b_j\right)\right|+\frac{1}{l_1{l}_3}\sum _{i=1}^{l_1}\sum _{k=1}^{l_3}\left|\rho \left(a_i,c_k\right)\right| \\ +\frac{1}{l_2{l}_3}\sum _{j=1}^{l_2}\sum _{k=1}^{l_3}\left|\rho \left(b_j,c_k\right)\right|). \end{gathered}$$ (29)

We permutate the row order of matrices A and B while keep the matrix C unchanged for Θ times. For each permutation, the mean correlation ${\rho }_{\theta }^{*}(\theta =1,2,\cdots ,\mathrm{\Theta })$ can be calculated by Eq. (29), which is used to build the null distribution of the mean correlation. By large number of permutations, the significance of the mean correlation can be evaluated by

$$\text{P-value}=\left|\left\{\theta \mid {\rho }_{\theta }^{*}\ge {\rho }^{*},\theta =1,2,\cdots ,\mathrm{\Theta }\right\}\right|/\mathrm{\Theta },$$ (30)

where | · | is the number of elements in the set. Variables with P-values smaller than 0.05/r were considered to be significant.

F. Parameter selection

For NMF-based model, how to determine the number of basis vectors r is still a challenging problem. If r is too large, the matrices will be over-factorized and we cannot achieve the goal of dimension reduction. If r is too small, e.g., r = 1, the limited basis vectors will represent the original data with a large residual error and we cannot discover the hidden skeleton in the datasets. A common method is to choose r based on the stability of the corresponding solutions [33]. Most of the time, we prefer a smaller value and let r ≪ min(m, n₁, n_2, n₃). The convergence tolerance was set to τ = 1 × 10⁻⁶. As for the regularization parameters λ₁, λ₂, λ₃, we apply grid search method based on variable stability selection to find the optimal value, which were proposed by Sun et al. in [34]. In Sun et al.’s work, there is only one sparse coefficient vector used to select variables. However, in our model, based on multiple coefficient vectors, we select multiple set of variables for the basis vectors simultaneously. Not all of the modules will be adopted in the following analysis and we just keep the modules with significant mean correlations defined in Eq. (29). In a word, we cannot use the pipeline in our model directly. Given a decreasing sequence for λ₁, λ₂, λ₃, we assume Λ = {Λ¹, Λ², ⋯, Λ^ν}, where ${\mathrm{\Lambda }}^j=\left[{\lambda }_1^j,{\lambda }_2^j,{\lambda }_3^j\right]$. is the j-th parameter combination (j = 1, 2, 3, ⋯, ν). The procedure of selecting the optimal combination of parameters is as follows:

1. The sample set was denoted as Ω and |Ω| = m, where m is the number of matrices rows. We randomly partition the Ω into two disjoint sets Ω¹ and Ω² and |Ω¹| = |Ω²| = m/2. If m is an odd number, we delete one sample randomly. For Λ^j, we perform the GSJNMF on Ω¹ and Ω² and obtain two sets of significant modules represented as $M_j^1$, $M_j^2$, respectively. The modules in these two sets were sorted by ascending order of P-values.

2. Assume ${\delta }^j=\min \left(\left|M_j^1\right|,\left|M_j^2\right|\right)$, $\delta =\max \left(1,\min \left\{{\delta }^1,{\delta }^2,\cdots ,{\delta }^{\nu }\right\}\right)$. Once we get δ, it will not change in the following operations.

3. For Λ^j (j = 1, 2, ⋯, ν), we rerun Step 1) and extract the top δ modules in $M_j^1$ and $M_j^2$. For each dataset and each sample set, we compute the union set of variables in the δ modules. For example, ${\mathcal{A}}_j^i$ is the union set of variables in the first dataset of Ωⁱ; ${\mathcal{B}}_j^i$ is the union set of variables in the second dataset of Ωⁱ; and ${\mathcal{C}}_j^i$ is the union set of variables in the third dataset of Ωⁱ (i = 1, 2).

4. The variable selection stability of the first dataset can be measured by Cohen’s kappa coefficient [35] as follows

   $$\kappa ({\mathcal{A}}_j^1,{\mathcal{A}}_j^2)=\frac{P_a\left({\mathcal{A}}_j^1,{\mathcal{A}}_j^2\right)-P_c\left({\mathcal{A}}_j^1,{\mathcal{A}}_j^2\right)}{1-P_c\left({\mathcal{A}}_j^1,{\mathcal{A}}_j^2\right)},$$ (31)

   where P_a is the relative probability of observed agreement and P_c is the hypothetical probability of chance agreement, which can be calculated by using the method in [34]. Analogically, the variable selection stability of the second and third datasets can also be measured. We use the mean value of these three Cohen’s kappa coefficient κ_j to represent the variable selection stability on the parameters combination Λ_j.
5. Repeat Step 3), 4) for D times and the d-th mean Cohen’s kappa coefficient for Λ^j is ${\kappa }_j^d$. The average variable selection stability of these D times repeats is given by

   $${\overline{\kappa }}_j=\frac{1}{D}\sum _{d=1}^D{\kappa }_j^d,j=1,2,\cdots ,\nu .$$ (32)

   We select the parameter combination, corresponding to the largest average variable selection stability.

IV. Materials and results

A. Simulation study

To assess the performance of the proposed GSJNMF model, we simulate three datasets with correlated components and then we compare JNMF and GSJNMF based on their abilities to identify the hidden associations within these simulated datasets. Since we want to simulate the group effect in the datasets, each dataset consists of some disjoint groups. The variables in a group are generated based on one single seed vector. For example, a group component with n variables can be denoted as

$$\alpha [n]=\left\{{\beta }_i\mid {\beta }_i=\alpha +\sigma {\eta }_i,i=1,2,\dots ,n\right\},$$ (33)

where $\alpha \in {ℝ}^m$ is a seed vector with entries randomly chosen from the standard normal distribution and ${\eta }_i\in {ℝ}^m$ is a Gaussian noise vector. $\sigma \in {ℝ}^{+}$ indicates the noise level. We arrange the column vectors β_i, $(i=1,2,\dots ,n)$ to form a sub-matrix of size m × n. The group components generated from the same seed vector are considered as correlated. Then these sub-matrices are concatenated to form the final data matrix. Based on the number of variables in each group and the number of groups in each data matrix, we generate four types of cases for the three data matrices in Table I, where “√” means equal while “×” means unequal. Two correlated group components are set across the three data matrices in all cases.

TABLE I.

The experiment setting of different cases

Case index	1	2	3	4
# groups in three data matrices	√	√	×	×
# variables in each group	√	×	√	×

In our simulation test, the length of variable vector m = 40. We generate the seed vectors randomly from the standard normal distribution and form the three data matrices as follows,

1. Case1: X₁ ← {α₁[20], α₂[20], α₃[20], α₄[20], α₅[20]}, X₂ ← {α₃[20], α₆[20], α₁[20], α₇[20], α₈[20]}, X₃ ← {α₉[20], α₁₀[20], α₁₁[20], α₃[20], α₁[20]}.

2. Case2: X₁ ← {α₁[15], α₂[5], α₃[9], α₄[12], α₅[10]}, X₂ ← {α₃[11], α₆[19], α₁[11], α₇[7], α₈[2]}, X₃ ← {α₉[6], α₃[8], α₁₀[17], α₁₁[18], α₁[6]}.

3. Case3: X₁ ← {α₁[20], α₂[20], α₃[20], α₄[20], α₅[20]}, X₂ ← {α₂[20], α₆[20], α₁[20]}, X₃ ← {α₇[20], α₈[20], α₉[20], α₁₀[20], α₁[20], α₁₁[20], α₂[20]}.

4. Case4: X₁ ← {α₁[10], α₂[13], α₃[8], α₄[9], α₅[11]}, X₂ ← {α₁[8], α₆[11], α₃[13]}, X₃ ← {α₇[8], α₈[9], α₃[12], α₉[10], α₁₀[7], α₁[13], α₁₁[11]}.

In each case, there are two correlated modules across the three data matrices. The corresponding variable indices of the correlated group components are displayed in Table II.

TABLE II.

The variable indices of modules in each case

Case index	Module index	Variable index
		X1	X2	X3
1	1	1 ∼ 20	41 ∼ 60	81 ∼ 100
	2	41 ∼ 60	1 ∼ 20	61 ∼ 80
2	1	1 ∼ 15	31 ∼ 41	50 ∼ 55
	2	21 ∼ 29	1 ∼ 11	7 ∼ 14
3	1	1 ∼ 20	41 ∼ 60	81 ∼ 100
	2	21 ∼ 40	1 ∼ 20	121 ∼ 140
4	1	1 ∼ 10	1 ∼ 8	47 ∼ 59
	2	24 ∼ 31	20 ∼ 32	18 ∼ 29

We normalize the three data matrices and make them to fit the constraints of nonnegativity with the following transformations. First, we standardize each column vector in the matrices to make the mean value be 0 and variance be 1. Second, we use the function F(x) = x − min(x)+ϵ to make each column be nonnegative, where x is the objective column vector and ϵ ∼ unif(0, 10⁻³). Third, we normalize each column vector to make the L₂ norm equal to 1. Fourth, we scale all the matrices so that the three data matrices have the same Frobenius norm. It is worth noting that the operations from the second to fourth step are all linear transformations, which will not change the Pearson correlation between the column vectors.

In the synthetic data experiments, because there are only two correlated modules in our design, we set r = 5 > 2. Since we identify the modules based on the z-score of each variables in the coefficient vectors, in each case we assess the performance of the GSJNMF and JNMF models by comparing the distribution of the z-scores of the variables in their identified modules. Based on the variable indices of the correlated module in Table II, we draw Figure A.1(a), A.2(a), A.3(a), A.4(a) (see Appendix A) to show the active variable indices in the four cases. The color of a line indicates a corresponding dataset. For example, red, blue and green means that the variables are from X₁, X₂ and X₃, respectively. In each case, we calculate the z-score of the 5 modules from JNMF and GSJNMF models and select the modules that are most likely to be the true correlated modules we generated. Three noise levels (σ = 0.5, 1, 1.5) are considered in each case and the z-scores of the variables of the two selected modules from JNMF and GSJNMF model are displayed in Figure A.1–A.4 (see Appendix A). A variable with a large z-score means that it is active in the module.

From the results of the four cases, we can know that the z-score of the variables in the modules from GSJNMF model can reflect the true correlated modules. When the noise level σ = 0.5, the z-scores of the variables in the same group are at the same level, and the z-score line looks very flat. If we increase the noise level to σ = 1, the GSJNMF model can still find the true correlated modules, but the z-score line becomes fluctuant. When the σ = 1.5, the fluctuation gets more severe. It’s worth noting that for all noise levels, the high z-score variables are all in the true correlated modules and the variables with Z-scores outside of the correlated modules are all very small. In this way, the GSJNMF model can identify the true variables in the modules.

As to the JNMF model, in the experiments of the four cases, even though the z-score of the variables in the true module are large, some variables outside of the true modules are still very large because of the fluctuations in the lines. These variables will be easily identified as wrong active variables. For example, in Figure A.1(a) (see Appendix A), the z-score of the variables (index from 21 to 40) from X₂ in JNMF-module2 are large, but are not the members of module2. When the noise level σ = 0.5, the distance between the lines in the large z-score region is relatively large. When the noise level σ = 1, the z-score lines become closer due to the increase of fluctuation and it is difficult to separate the true modules from the whole variables. When the noise level σ = 1.5, the fluctuations become more severe and we can hardly get any module information from the lines.

From this comparison, we can know that JNMF model is more sensitive to noise. In GSJNMF model, even though there are some fluctuations, the z-score lines still reflect the true variables in each module. When there exists group structure in the datasets, GSJNMF can employ this group information and improve performance.

B. Data preparation and preprocessing

Participants in this study were from the Mind Clinical Imaging Consortium (MCIC). 80 SZ patients (age: 34±11, 20 females) and 104 healthy controls (age: 32 ± 11, 38 females) were analyzed here. We used three types of datasets (e.g., SNP, fMRI, DNA methylation data) of the 184 samples. Each SNP was categorized into three clusters based on their genotype and was represented with discrete numbers: 0 for ‘BB’ (no minor allele), 1 for ‘AB’ (one minor allele) and 2 for ‘AA’ (two minor alleles). The fMRI data were extracted with 53×63×46 voxels and all the voxels with missing measurements were excluded. 116 ROIs were extracted based on the AAL brain atlas. DNA from blood samples was assessed by the Illumina Infinium Methylation27 Assay. A methylation value represents the ratio of the methylated probe intensity to the total probe intensity. We followed the same preprocessing procedures in [12] for SNP and fMRI, as well as the one [11] for DNA methylation, resulting in 722,177 SNPs, 41,236 fMRI voxels and 27,508 methylation sites, respectively. Since we want to find the biomarkers only associated with SZ, we applied the t-test to these three datasets between SZ and healthy samples, and only selected those variables with P-value < 0.05. For SNP data, we only keep the SNPs included in the Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway [36]. After variable selection, we obtained 10,351 SNPs, 2,428 fMRI voxels and 2,724 methylation sites in 2,006 genes, 76 brain regions, 2,134 genes from 184 samples, which were represented in three matrices $X_1\in {ℝ}^{184\times 10351}$, $X_2\in {ℝ}^{184\times 2428}$ and $X_3\in {ℝ}^{184\times 2724}$, respectively. We used the same procedure to process the three data matrices and normalize them to the same value level. We then applied the GSJNMF model to the three matrices.

C. Module discovery and validation

The variables in SNP, fMRI and DNA methylation datasets were grouped based on the genes and brain regions of interest (ROIs) (e.g., SNPs within the same gene, voxels within the same region, and methylation sites within the same gene). As a result, there were 2,006 groups in X₁, 76 groups in X₂, 2134 groups in X₃ and these groups have different sizes. We then performed the GSJNMF model on the preprocessed datasets to identify multi-dimensional modules. In our test, we set the number of basis vectors r = 20 and the threshold for z-score T = 3 corresponding to the P-value = 0.0013 < 0.01. We searched the regularization parameters in $\{0.1\times \frac{1}{2^n}\mid n=1,2,\cdots ,10\}$ and set λ₁ = 1.9531 × 10⁻⁴, and λ₂ = λ₃ = 0.025 by using the proposed selection procedure. The three data matrices were broken down into 20 basic building blocks, which capture the major information embedded in the original data. In other words, the variables in the three datasets can be linearly represented with the 20 basis vectors. For each basis vector, we identified a module, which consists of multiple variables from the three datasets. Within the 20 modules, four of them were significantly correlated, and these four modules were used for the subsequent analysis. Table III and IV provide the gene lists within the four modules identified from the SNP variables and DNA methylation sites, respectively. The brain ROIs identified from the fMRI voxels are displayed in Table V, where ‘*’ means null and each voxel’s volume is 3×3×3 mm³.

TABLE III.

The list of genes selected from the significantly identified modules

Module	Gene ID (SNP)
1	VTI1B, DNMT3B, NFX1, NUMB, SEC61G, ASS1, ACTG2, ADCY2, FOXO3, ABCA12, PAK3, COL4A2, DIAPH2, GOT2, NCOR2, DCC, PRKG1, PLA2G4A
2	NLN, AVPR1A, NCOR2, IL7, MAN1A1, PLA2G4A, CD28
3	CACNG5, SGPP2, MKNK1, MASP1, PRKCQ, FUCA2, NDST4, GRIK2, ERBB4, FUT8, CBLB, RYR2, PRKG1, NEGR1, NRG1
4	ATM, ACP6, TGFBR2, GNA14, PPP1R12A, CTNNA2, PLXNA2

TABLE IV.

The list of genes selected from significantly identified modules

Module	Gene ID (DNA methylation)
1	FLJ22746, FLJ11155, CDKN2A, C10orf26, C10orf10, CDH13,
2	BRDT, EEF1E1, IKIP, MYO9A, LOC400696
3	C1orf26, FLJ11017, MICA, GMPR, COMMD5, WDR68, DCC,
4	FCGR3B, FLJ20245, NTNG2, TUB, DGAT2L6

TABLE V.

Brain regions detected from significantly identified modules

Brain region╲Module	L/R volumn(cm3)
	1	2	3	4
Insula	*	*	1.296/*	*
Lingual Gyrus	*	0.432/*	*	*
Fusiform Gyrus	*	*/0.678	*	*
Postcentral Gyrus	*	*	1.944/*	2.403/*
Supramarginal Gyrus	*	*	0.648/1.107	*
Superior Temporal Gyrus	*	0.486/*	0.486/*	*
Superior Temporal Pole	*	*	0.405/*	*
Lobule VI of Cerebellar Hemisphere	0.486/*	*	*	*

In the 1-st module, there are 18 genes identified from SNPs, 6 genes from DNA methylations and 1 brain ROIs from fMRI, which can be further validated. Among them, DNMT3B may increase the risk for SZ because of the gene-gene interaction with DRD1 [37]. DCC is a promising novel candidate gene that may contribute to the genetic basis behind individual differences in susceptibility to SZ [38]. PRKG1 [39] has shown its association with SZ with the 21-st most significant SNP in the CATIE GWAS [40]. PRKG1 also interacts with RGS2 and GABRR1, which has modest association with SZ symptoms [41] and schizoaffective disorder [42]. The PLA2G4A gene has been found to be associated with negative symptoms of SZ [43]. The abnormalities of PLA2G4A may be involved in a subgroup of the illness. C10orf26 as one of the target gene of miR-137 was also reported to have genome-wide significant associations with SZ [44]. CDH13 has been implicated in the susceptibility to a variety of psychiatric diseases, which may contribute to the genetic risk of SZ [45], [46].

In the 2-nd module, there are 7 genes identified from SNP, 5 genes identified from DNA methylation and 3 brain ROIs identified from fMRI. CD28 gene polymorphisms may not only act in immune deregulation observed in SZ, but may also influence the course of the illness by modifying the susceptibility to the co-occurrence of psychotic and affective symptoms [47]. In [48], fMRI results showed reduced clusters of activation in left lingual gyrus in SZ subjects as compared to controls during empathy task, which means that the left lingual gyrus is associated with empathy in SZ patients. The bilateral reduction in fusiform gyrus [49] and progressive reduction in left superior temporal gyrus [50] gray matter volume are associated with SZ patients in first-episode.

In the 3-rd module, 15 genes from SNP, 7 genes from DNA methylation and 6 brain ROIs were identified. A real effect of variation on CACNG5 may modify the susceptibility to SZ, which means CACNG5 might contribute to the risk of SZ [51]. The maternal GRIK2 transmission disequilibrium previously reported for autism supports that GRIK2 is a susceptibility gene for SZ [52]. NRG1 and ERBB4, critical neurodevelopmental genes, are implicated in SZ [53]. FUT8 may associate with SZ because of its lower expression [54]. Within insula, abnormalities in gray matter volume, cortical thickness, cellular structure and the expression of proteins can be observed in SZ, which means insula may play an important role in the development of SZ [55]. The SZ patients’ gray matter in left postcentral gyrus significantly decreases relative to the control group, indicating that the left postcentral gyrus maybe associated to the SZ [56].

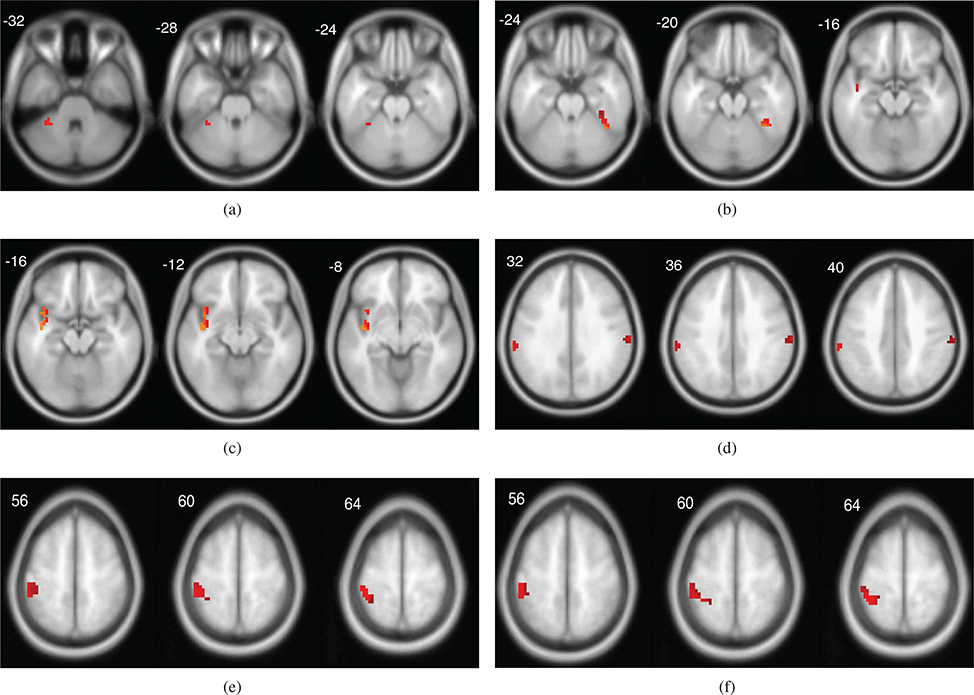
In the 4-th module, we identified 7 genes from SNP, 5 genes from DNA methylation and 1 brain ROI from fMRI dataset. ATM was considered as one of the biomarker genes to discriminate SZ from controls. The combination of ATM and ADSS may confer susceptibility to the development of SZ [57]. Since the TGFBR2 mRNA levels in the peripheral leukocytes may be a potential state marker for SZ, TGFBR2 gene may be involved in the pathogenesis of SZ [58]. CTNNA2 is differentially regulated by smoking in SZ patients and it represents a promising candidate gene for SZ based on previous genetic linkage and expression study [59]. PLXNA2 is involved in axonal guidance during development and may modulate neuronal plasticity and regeneration and the PLXNA2 ligand semaphorin 3A is upregulated in the cerebellum of SZ patients, which means PLXNA2 is likely a candidate susceptibility gene for SZ [60]. We also plot the selected fMRI voxels corresponding to the four modules in Figure 1.

Fig. 1.

(a) Brain ROIs in module 1 (b) Brain ROIs in module 2. (c,d,e) Brain ROIs in module 3. (f) Brain ROIs in module 4. The color indicates the z-score value of the selected voxels.

From the above analysis, each module contains significant biomarkers, which correspond to genes and brain ROIs related to SZ supported with existing literatures. Moreover, the genes and brain ROIs within the same module are significant correlated numerically. It indicates that these biomarkers may also have some functional associations with SZ. For real data integration, since we don’t have the ground truth, the genes and ROIs not reported in the literatures may contribute to new candidate biomarkers associated with SZ. These biomarkers in the same module and their correlation with clinical outcomes need to be further verified by the biologists. We also found that there are some genes and ROIs overlapping between the modules. For example, NCOR2 and PLA2G4A correspond to both 1-st and 2-nd modules’ SNP components. PRKG1 corresponds to the 1-st and 3-rd modules’ SNP component. DCC is derived from the 1-st module’s SNP component and 3-rd module’s DNA methylation component. The left postcentral gyrus is shown in 3-rd and 4-th modules’ fMRI component. The left superior temporal gyrus appears in 2-nd and 3-rd modules’ fMRI component. These overlaps among the multi-dimensional modules may infer that these genes and ROIs are active and involved with multiple biological and brain functions. All these findings therefore demonstrate the implications of the selected modules related to SZ.

V. Conclusions

SNP, fMRI and DNA methylation provide important and complementary information about SZ, but most existing approaches either focus on one or two datasets analysis. If we represent the three datasets as a joint matrix with rows for the same subjects, JNMF simultaneously projects the matrices into a lower dimension subspace shared by the three datasets and the nonnegative coefficient values for each matrix can be used to select significantly correlated features among the three datasets. Since the SNP, fMRI and DNA methylation datasets have group structures (e.g., multiple SNPs spanning a gene, a group of voxels within a ROI, and multiple methylation sites within a gene), we can take advantage of the group information to improve the JNMF model. In other words, our GSJNMF model can incorporate prior knowledge by enforcing group sparse constrains into the corresponding coefficient matrices in the model. As a result, the hidden dependence structures can be identified and the data heterogeneity in the datesets can also be reflected. In addition, the new GSJNMF model will render the results to be more easily interpretable. The model is finally validated by applying to the real imaging genomic data from MCIC to identify significant genes or biomarkers associated with SZ. In the future, we will incorporate gene networks and/or brain region network information into our analysis model. Although in this work we focus on the study of SZ, the model can be applicable to the study of many other diseases, where multi-omics data are ubiquitous.

Biography

Min Wang received the B.S. degree from the School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, China, in 2012, where he is currently pursuing the PhD degree with the School of Mathematical Sciences. His current research interests include image processing, biomedical imaging and bioinformatics.

Ting-Zhu Huang is currently a Professor with the School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, China. He received the B.S. degree, the M.S. degree, and the PhD degree from Xi’an Jiaotong University, Xi’an, China, in 1986, 1992, and 2001, respectively. His current research interests include numerical linear algebra and scientific computation with applications in electromagnetics, modeling, and algorithms for image processing. He has authored over 100 papers in international journals, including the SIAM Journal on Scientific Computing, the SIAM Journal on Matrix Analysis and Applications, the IMA Journal of Numerical Analysis, the Journal of Computational Physics, Computer Physics Communications, Numerical Linear Algebra with Applications, Automatica, the IEEE TRANSACTIONS ON ANTENNAS AND PROPAGATION, the IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, Information Sciences, the Journal of the Optical Society of America A, Computing, Linear Algebra and its Applications, Applied Mathematics Letters, Computers and Mathematics with Applications, Applied Mathematical Modelling, the Journal of The Franklin Institute, the Journal of Computational and Applied Mathematics, and Communications in Nonlinear Science and Numerical Simulation. Dr. Huang received the Science and Technology Progress Award of Sichuan Province from the Chinese Information Ministry for several times. He has served on the Editorial Board of several international journals.

Jian Fang received the B.S. degree in mathematics from Nanjing Normal University, Nanjing, China, in 2008, and the PhD degree in Applied Mathematics from Xi’an Jiaotong University, China, in 2016. He is currently a Postdoctoral Fellow of Biomedical Engineering at Tulane University School of Science and Engineering. His research interests include signal processing, sparse modeling, machine learning, and their applications to the integration of multi-omics and biomedical imaging data.

Vince D. Calhoun received the bachelor degree in electrical engineering from the University of Kansas, Lawrence, Kansas, in 1991, master degree in biomedical engineering and information systems from Johns Hopkins University, Baltimore, in 1993 and 1996, respectively, and the PhD degree in electrical engineering from the University of Maryland Baltimore County, Baltimore, in 2002. He worked as a senior research engineer at the psychiatric neuroimaging laboratory at Johns Hopkins from 1993 until 2002. He then served as the director of medical image analysis at the Olin Neuropsychiatry Research Center and as an associate professor at Yale University. He is currently the chief technology officer and the director of Image Analysis and MR Research at the Mind Research Network and is a professor in the Departments of Electrical and Computer Engineering (primary), Neurosciences, Psychiatry and Computer Science at the University of New Mexico. He is the author of more than 650 full journal articles and more than 300 technical reports, abstracts, and conference proceedings. Much of his career has been spent on the development of data driven approaches for the analysis of brain imaging data. He has won more than $18 million in NSF and NIH grants on the incorporation of prior information into independent component analysis (ICA) for functional magnetic resonance imaging, data fusion of multimodal imaging and genetics data, and the identification of biomarkers for disease. He is a chartered grant reviewer for NIH. He has organized workshops and special sessions at multiple conferences. He is currently serving on the IEEE Machine Learning for Signal Processing (MLSP) technical committee and previously served as the general chair of the 2005 meeting. He is a reviewer for many journals and is on the editorial board of the Human Brain Mapping and Neuroimage journals. He is a senior member of the IEEE, the Organization for Human Brain Mapping, the International Society for Magnetic Resonance in Medicine, and the American College of Neuropsychopharmacology.

Yu-Ping Wang received the B.S. degree in applied mathematics from Tianjin University, China, in 1990, and the M.S. degree in computational mathematics and the PhD degree in communications and electronic systems from Xi’an Jiaotong University, China, in 1993 and 1996, respectively. After his graduation, he had visiting positions at the Center for Wavelets, Approximation and Information Processing of the National University of Singapore and Washington University Medical School in St. Louis. From 2000 to 2003, he worked as a senior research engineer at Perceptive Scientific Instruments, Inc., and then Advanced Digital Imaging Research, LLC, Houston, Texas. In the fall of 2003, he returned to academia as an assistant professor of computer science and electrical engineering with the University of Missouri-Kansas City. He is currently a professor of biomedical engineering and biostatistics & bioinformatics with the Tulane University School of Science and Engineering & School of Public Health and Tropical Medicine. He is also a member of the Tulane Center of Bioinformatics and Genomics, Tulane Cancer Center, and Tulane Neuroscience Program. His research interests include computer vision, signal processing, and machine learning with applications to biomedical imaging and bioinformatics, where he has over 200 peer reviewed publications. He has served on numerous program committees and NSF/NIH review panels, and served as editors for several journals such as Neuroscience Methods. He is a senior member of the IEEE.