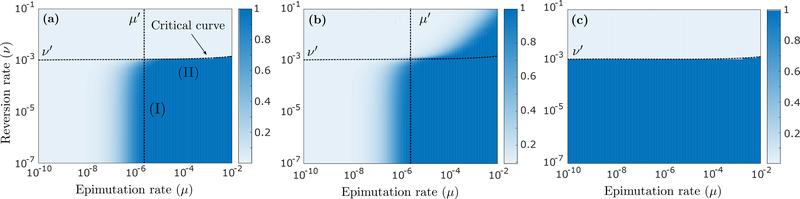
Figure 3:
(a) Probability that the tumor survives continuous anti-cancer therapy, as a function of μ and ν, assuming n = 106 and m = 0 and the absence of permanent resistance mechanisms (η = 0 and ξ0 = ξ1 = 0), calculated using (C.2). The black dotted curve (’critical curve’) separates the regions in the (μ, ν) plane where the population is subcritical (top) and supercritical (bottom). This curve can be extracted from expression (10) upon logarithmic scaling (see Fig 2a). Region (I) in the figure indicates a parameter regime where inhibiting epimutations (decreasing μ) with an epigenetic drug can be an effective treatment strategy, whereas inducing reversions (increasing ν) does little. The reverse is true in the parameter regime of region (II), where a slight perturbation to the reversion rate ν can guarantee eradication of the tumor cell population. (b) Same as (a), now assuming η = 4 · 10−7 (per hour) and ξ0 = ξ1 = 10−7 (per cell division), calculated using (G.5). (c) Same as (a), now assuming n = 106 · 0.999 and m = 106 · 0.001, calculated using (C.2). Other parameter values are r0 = 0.04 (per hour), d0 = 0.08, r1 = 0.0162, d1 = 0.015, μ = 4 · 10−5 and ν = 4 · 10−4.