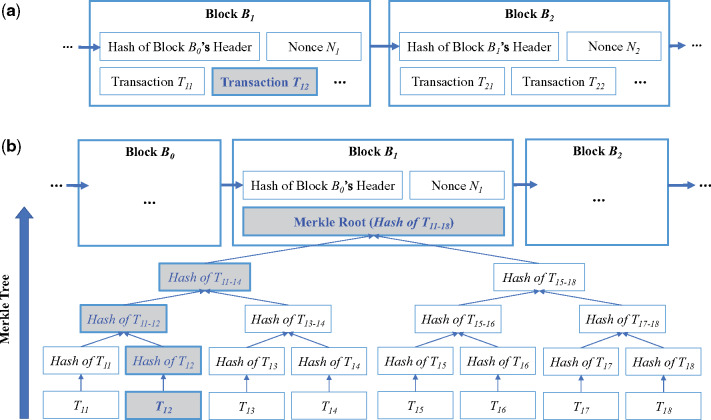
Figure 2.
To reduce storage, if a block B is “voted” to be correct because the chain is long enough (ie, there are already many blocks created after B), we can discard the transactions contained in B, without changing the hash of B’s header (otherwise all blocks after B would need to be changed). To do this, instead of saving the content of all transactions directly in a block, we first compute the hash values of each transaction, and then construct a tree structure (a Merkle tree),26–28 to “combine” (ie, hash again) all hash values, and store only the Merkle Root hash value at the block header. This way we can prune the transactions in the tree later, without changing the Merkle Root and the block header. In other words, the size of the blockchain is now proportional to the number of blocks instead of being proportional to the number of transactions. (A) An example blockchain without a Merkle tree. The blocks enclose transactions without adopting a Merkle tree. As a result, the size of a block will grow proportionally to the number of transactions (eg, transaction T12) that are enclosed. (B) A blockchain with a Merkle tree. A Merkle tree is constructed by hashing paired data (the leaves) to create a parent node iteratively, until a single hash, the Merkle Root,1 remains. In this example, the transactions (eg, T12) are first encoded into a binary raw-transaction format and then hashed to create the hashes (eg, Hash of T12). Then, hashes such as the Hash of T12 are paired with other hashes such as the Hash of T11 (if a hash does not have a pair, it simply duplicates itself to be paired) to compute the hash as their parent node (ie, Hash of T11–12). The pairing/hashing process repeats until only 1 hash (the Merkle Root) remains, and the Merkle tree construction process is then completed. Finally, by only enclosing the Merkle Root in each block header, the storage space required to verify the integrity/validity of transactions can be reduced.56 That is, if an attacker tries to change the content of any transaction such as T12, all of the related hashes (ie, Hash of T12, Hash of T11–12, and Hash of T11–14), and eventually the Merkle Root (ie, Hash of T11–18) will also change and can be easily verified. To enclose this new Merkle Root to pass the verification process, the attacker then needs to re-create block B1 and all blocks thereafter, which is computationally expensive and is enough to prevent such modification.2,57 A Merkle tree is the basis of lightweight nodes described in Figure 3 (ie, the blockchain nodes that only need to verify transactions can store parts of the Merkle trees to save space, while the full blockchain nodes that need to “mine” new blocks store all of the Merkle trees).