Fig. 3. Rotational dynamics of particles under linearly polarized illumination.

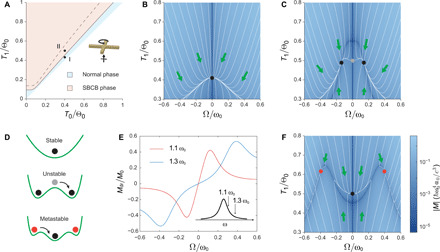
(A) Stability of the nanocross considered in Fig. 2 (B and E) at rest under linearly polarized illumination of frequency ω = 1.1ω₀ (solid curve) and 1.3ω₀ (dashed curve), as a function of vacuum and particle temperatures T₀ and T₁ normalized to Θ₀ = ħω₀/k_B. For each value of T₀, a steady particle temperature T₁ is reached at a laser intensity I(T₁). The black solid and dashed curves denote phase boundaries for frequencies ω = 1.1ω₀ and 1.3ω₀, respectively. (B and C) Evolution of the nanocross at arbitrary initial T₁ and Ω for light frequency ω = 1.1ω₀, with vacuum temperature T₀ = 0.4Θ₀ and laser intensities I(0.41Θ₀) (B) or I(0.5Θ₀) (C), which correspond to the black dots I and II in (A). (D) Illustration of the particle state in different phases. Top: The equilibrium state at Ω = 0 is stable [black dot, also in (B)]. Middle: The equilibrium state at Ω = 0 is unstable for high light intensity [gray dot, also in (C)]. Bottom: A metastable configuration (see below). (E) Driving torque acting on the particle rotating at different velocities Ω for light frequencies ω = 1.1ω₀ and 1.3ω₀. (F) Same as (C) for light frequency ω = 1.3ω₀. Two metastable configurations are observed, yielding the equilibrium at Ω = 0 stable [point II in (A) is in the normal phase for ω = 1.3ω₀], which is intuitively illustrated in the bottom panel of (D).