Validation of a GPU-based Monte Carlo code (gPMC) for proton radiation therapy: clinical cases study

Abstract

Purpose:

Monte Carlo (MC) methods are recognized as the gold-standard for dose calculation, however they have not replaced analytical methods up to now due to their lengthy calculation times. GPU-based applications allow MC dose calculations to be performed on time scales comparable to conventional analytical algorithms. This study focuses on validating our GPU-based MC code for proton dose calculation (gPMC) using an experimentally validated multi-purpose MC code (TOPAS) and compare their performance for clinical patient cases.

Methods:

Clinical cases from five treatment sites were selected covering the full range from very homogeneous patient geometries (liver) to patients with high geometrical complexity (air cavities and density heterogeneities in head-and-neck and lung patients) and from short beam range (breast) to large beam range (prostate). Both gPMC and TOPAS were used to calculate 3-dimensional dose distributions for all patients. Comparisons were performed based on target coverage indices (mean dose, V₉₅, D₉₈, D₅₀, D₀₂) and gamma index distributions.

Results:

Dosimetric indices differed less than 2% between TOPAS and gPMC dose distributions for most cases. Gamma index analysis with 1%/1mm criterion resulted in passing rate of more than 94% of all patient voxels receiving more than 10% of the mean target dose, for all patients except for prostate cases. Although clinically insignificant, gPMC resulted in systematic underestimation of target dose for prostate cases by 1–2% compared to TOPAS. Correspondingly the gamma index analysis with 1%/1mm criterion failed for most beams for this site, while for 2%/1mm criterion passing rates of more than 94.6% of all patient voxels were observed. For the same initial number of simulated particles, calculation time for a single beam for a typical head and neck patient plan decreased from 4 CPU hours per million particles (2.8–2.9GHz Intel X5600) for TOPAS to 2.4 sec per million particles (NVIDIA TESLA C2075) for gPMC.

Conclusions:

Excellent agreement was demonstrated between our fast GPU-based MC code (gPMC) and a previously extensively validated multi-purpose MC code (TOPAS) for a comprehensive set of clinical patient cases. This shows that MC dose calculations in proton therapy can be performed on time scales comparable to analytical algorithms with accuracy comparable to state-of-the-art CPU-based MC codes.

1. Introduction:

The number of proton radiation therapy facilities is constantly increasing. With new technological advances, new options for treatment plan design and verification become available. Concepts to improve treatment plans continue to be developed, such as intensity modulated proton therapy (IMPT), image guided proton therapy (IGPT) and adaptive proton therapy (APT). In current clinical practice, treatment plans are generally created using analytical dose calculation methods due to their short calculation time. However, in order to achieve fast dose calculations, several approximations have to be made in analytical algorithms, occasionally compromising the accuracy (Schuemann et al 2014). It has been shown that analytical calculations do not predict multiple-Coulomb scattering accurately, which results in an increasing discrepancy between the calculated and actual dose distributions with increasing patient heterogeneity (Schuemann et al 2014, Yang et al 2012, Sawakuchi et al 2008, Bueno et al 2013, Paganetti 2012). To account for the uncertainties in dose calculation and delivery, margins are introduced in the delineation of target volumes. It has been shown that uncertainties in dose calculations can be reduced significantly using Monte Carlo (MC) simulations (Paganetti 2012). Recently, some treatment planning systems (TPSs) for proton therapy include the option to run post-planning MC-based dose verification, and there is currently one commercial treatment planning system offering the option for MC based plan optimization. The main reason for the limited availability of MC-based proton treatment planning or re-planning options is the relatively long computation time of full MC simulations (Parodi et al 2007, Schümann et al 2012). For example, to achieve acceptable levels of statistical uncertainty, the computation time for a head-and-neck patient dose distribution from a typical single beam, using the Geant4 (Agostinelli et al 2003, Allison et al 2006) based TOPAS MC toolkit (Perl et al 2012), is 135 CPU hours on a 2.8–2.9GHz Intel X5600.

In order to make MC simulations available for treatment planning, IGPT or APT, dose calculations have to be extremely fast, i.e. in the order of a few seconds. Graphical processing units (GPUs) are a frequently used option to achieve fast calculations and several efforts to use GPUs for MC simulations are underway. Yepes et al have suggested a GPU-based track-repeating fast dose calculation algorithm utilizing a pre-generated database of histories of particles produced by a proton impinging on a water phantom (Yepes et al 2010). We have recently developed a GPU-based code for proton dose calculations (Jia et al 2012) implementing full simulation of each particle history, without any track-repeating process. Compared to a recently published approach (Tseung et al 2014), instead of using a detailed modeling of non-elastic interactions, our code, GPU Proton Monte Carlo (gPMC), follows an empirical strategy developed by Fippel and Soukup (Fippel and Soukup 2004). With 448 thread processors available on an Nvidia C2050 GPU card, gPMC achieves single field dose calculations in the order of 10 seconds. Note that the actual number of threads executed concurrently is less than the processor number depending on how the GPU manages the proton transport kernel executions. The results has been compared against dose distributions calculated with TOPAS (based on Geant4) for phantom geometries and a single, non-clinical field on a patient computed tomography (CT) volume (Jia et al 2012).

In this study, we expand our previous effort to validate gPMC against TOPAS for a comprehensive set of clinical patient cases. Previously delivered treatment plans for five clinical sites, including 30 patients in total, were calculated using both MC codes. The impact of the different MC algorithms on clinically relevant dosimetric indices, extracted from dose volume histograms (DVH), was investigated. To verify the systematic agreement between the full three-dimensional (3D) dose distribution produced by TOPAS and gPMC, the gamma index method was employed.

2. Methods:

2.1. GPU-based proton Monte Carlo simulations using gPMC

Our GPU-based MC code used in this study, gPMC, was described in detail previously (Jia et al 2012). It follows various publications (Agostinelli et al 2003, Kawrakow 2000, Fippel and Soukup 2004, Salvat and Fernández-Varea 2009) for the physics implementation and is written in CUDA (docs.nvidia.com). It employs various innovative techniques to optimize calculation speed and to avoid memory writing conflicts. The physics settings for neutral and charged particles as well as their handling was described in our previous publication (Jia et al 2012).

For every patient included in the study, dose-to-water (Paganetti 2009) was calculated on the planning CT grid. The patient CT usually consists of a varying number of axial slices, usually between 70 and 300 with thickness between 1.25 mm and 3.75 mm, depending on the treatment site. Each slice had a resolution of 512×512 voxels corresponding to a voxel size of less than 1×1 mm² in most cases. gPMC has the option to score doses on a different, user-defined dose grid. For this study the dose distributions were computed on the original clinical dose calculation grid, which has a default resolution of 2 × 2 × 2.5 mm³. To obtain the dose distribution on a user-defined grid, the dose for each voxel is re-calculated using trilinear interpolation based on the calculated dose for the 8 surrounding voxels of the original CT grid.

2.2. TOPAS Monte Carlo

The Geant4-based TOPAS MC toolkit was selected as the gold standard and reference for this study. TOPAS has been extensively validated (Testa et al 2013) versus measurements, using clinically relevant ranges and modulation widths measured at the Francis H. Burr Proton Therapy Center at MGH. Both ranges and modulation widths, as calculated by TOPAS, were found to agree with measurements within clinical requirements. Additional validation procedures were performed, including but not limited to, dose verification using inhomogeneous phantoms and multi-layer Faraday cups, dose rate functions and output factors measured by ion chambers inside the treatment head (Testa et al 2013).

For this study, we used TOPAS version beta 8, based on Geant4.9.6.p02. The standard physics settings, secondary production cuts and step sizes of the TOPAS package were used (Perl et al 2012, Testa et al 2013). Dose-to-water is calculated on the patient planning CT grid. TOPAS allows users to specify different dose calculation grids for scoring, in which case the dose to each voxel is calculated by volumetric interpolation. In this study we scored dose-to-water on the same clinical dose calculation grid as described in the previous section.

2.3. Patient data and calculation process

Previously delivered treatment plans were selected from the MGH patient database, for a total of 30 patients treated for five clinical sites: breast, head-and-neck, liver, lung and prostate. Patients selected for each clinical site had a variety of prescription doses and target volumes. Table 1 summarizes the clinical data set.

Table 1:

Treatment data of the clinical cases under study

Treatment Site	Number of patients	Range of Target Volumes [cc]	Range of Prescription Dose [Gy(RBE)]	Range of Ranges [mm]	Range of Modulation widths [mm]
Lung	4	114–439	35–75	99–175	53–114
Breast	7	358–1274	45–50.4	53–102	18–98
Head-and-Neck	11	22–134	54–76	53–195	16–139
Liver	4	139–459	7.74–58.05	109–194	73–133
Prostate	4	30–178	33–79	230–271	66–122

For every patient, the original treatment plan CT image set and beam geometry were imported into TOPAS via a software script used routinely for MC dose calculation of proton patients at MGH. For each treatment field, the path of a proton beam of appropriate energy was simulated through the specific nozzle geometry using TOPAS and the result was scored as a phase space file at the exit of the treatment head, which included the corresponding aperture and range compensator elements. A total number of 7.5 million original histories per beam were simulated at this first part of the calculation. Variance reduction techniques were used (Ramos-Méndez et al 2013), splitting each initial history to 64, resulting in a total number of 480 million initial particles per beam. The number of particles in each resulting phase space file varied depending on the treatment site, initial proton energy and tumor size. Each phase space file was used as a source by both the gPMC and the TOPAS MC codes for the simulation of particle tracking through the patient geometry.

The dose in the patient was scored as dose-to-water and was normalized to the prescribed dose per beam in the same way for both MC codes following the method described in Schuemann et al (Schuemann et al 2014): a treatment field-specific normalization factor was obtained by simulating the SOBP dose distribution in a water phantom, which mimics the actual clinical dose normalization. The resulting dose distributions for individual beams as well as the total dose distributions, i.e the summation of all individual beams for each patient, were then compared for the two MC codes.

2.4. Analysis method

Comparison between the dose calculations by the two MC codes was performed in terms of 3D dose distributions, DVH results and gamma index analysis (Low et al 1998, Clasie et al 2012).

2.4.1. Dosimetric analysis

Based on the calculated 3D dose distributions and patient structure set, the DVHs were obtained for target structures specified either as the clinical target volume (CTV) or planning target volume (PTV), depending on treatment planning method and site. Several DVH indices were then used as surrogates to quantitatively compare the DVHs obtained from the two different MC codes:

• Mean target dose: dose averaged over all voxels in the target

• V₉₅: percent target volume covered by 95% of the prescription dose for the specific target

• D₉₈: maximum dose covering 98% of the target volume (surrogate index for minimum dose)

• D₅₀: median target dose

• D₀₂: maximum dose covering 2% of the target volume (surrogate index for maximum dose)

2.4.2. Gamma index analysis

The 3D gamma index distribution (Low et al 1998), (Clasie et al 2012) was calculated for every beam as well as the complete treatment plans for all patients under study, using a criterion of 1mm and 1% of the reference dose (TOPAS calculated dose) in each voxel. For the prostate cases additional gamma analysis was performed using a criterion of 1mm and 2% of the reference dose. A dose threshold of 10% of the mean target dose received by the searched (gPMC) 3D dose cube was used. The percentage of voxels passing the gamma criterion was defined for each clinical target volume and for the whole patient.

3. Results

3.1. Dosimetric analysis

Two-dimensional comparison of the dose distributions as calculated by the two MC methods shows very good agreement. Figure 1 presents the dose distributions calculated by TOPAS (figure1a) and gPMC (figure 1b), their dose difference distribution (figure 1c) and DVHs (figure 1d) for a head-and-neck patient, as a representative example. The dose comparison in this case shows almost identical dose distributions for both methods, resulting in differences of less than 2% (1.6 Gy(RBE)) of the maximum dose (80 Gy(RBE) for this case) for most voxels within the treatment field (figure 1c).

Figure 1:

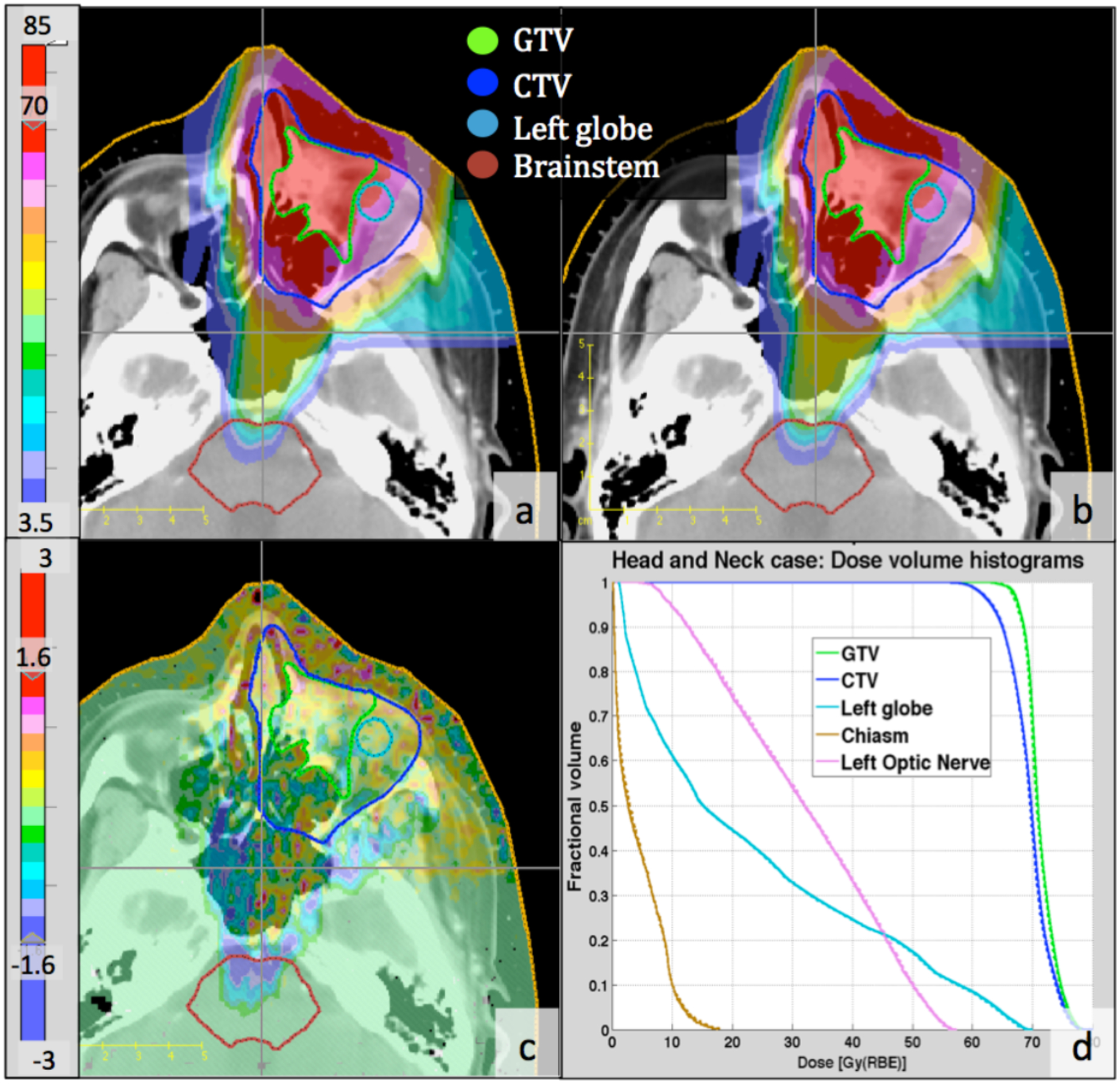
Two-dimensional and DVH comparison between gPMC and TOPAS calculated doses for a head- and-neck case, (a): gPMC-calculated dose distribution; (b): TOPAS-calculated dose distribution; (c): Absolute dose difference (gPMC - TOPAS); (d): DVHs for targets and OARs; Solid lines: gPMC; Dashed lines: TOPAS. Colorbars on the left are in units of Gy(RBE).

All dosimetric indices mentioned in paragraph 2.4.1 were calculated by both MC codes for the target volume and the full dose distribution of each patient. The corresponding relative difference with reference to the TOPAS dose was obtained for each dosimetric index as presented in figure 2. Every data point in figure 2 corresponds to the relative difference of a dosimetric index.

Figure 2:

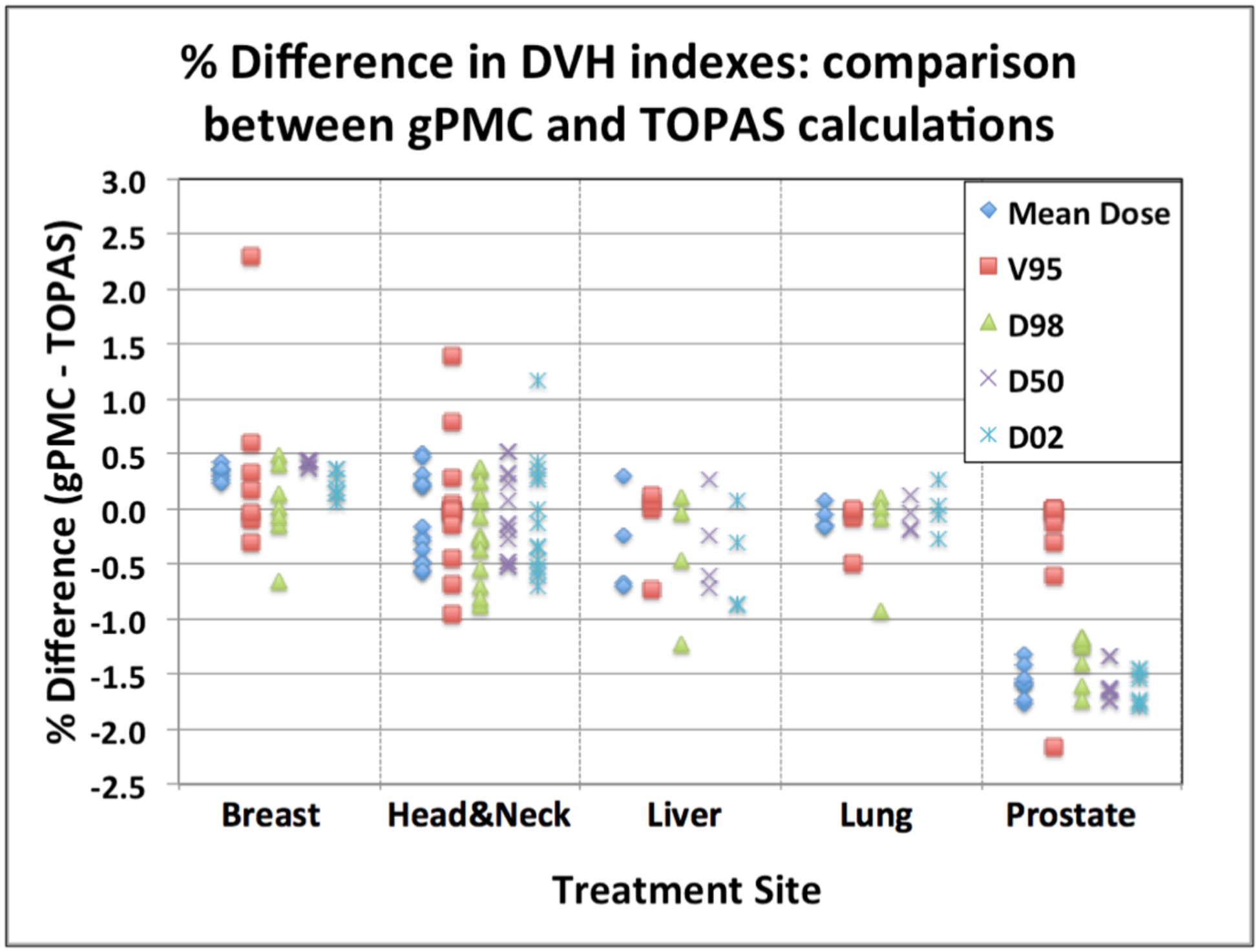
Percent discrepancies of dosimetric evaluators for the target volumes: comparison between gPMC and TOPAS calculations. Data for all patients are displayed, grouped per treatment site. Each point corresponds to the difference in the dosimetric represented by the symbol for the target volume of a patient belonging to the treatment site given at the bottom of the graph section.

The gPMC calculated mean dose for all patients is within ±1% of the TOPAS calculated doses. For all breast and lung cases, as well as for 12 out of 14 head-and-neck targets under study, the agreement was within 0.5%. D₉₈, median dose (D₅₀) and D₀₂, as calculated by gPMC, is within ±1% of the TOPAS results for most patients, except for the prostate cases, where differences of −1% to −2% were observed for all cases. Although systematic, these differences are not considered clinically significant, since they are below 2%. Minimum clinically acceptable target coverage as given by the V₉₅ index was also within ±1% agreement between the two codes for 27 out of 30 patient cases and within ±2% for 28 of the patients.

3.2. Gamma index analysis

The results for the gamma index analysis are shown in Tables 2a and 2b, along with the target volume and the corresponding prescription dose for each patient. When accounting only for the voxels in the target volume and the treatment field for the full plan, an excellent passing rate of more than 96.9%, for 1%/1mm criterion, was observed for the cases in all clinical sites, except for prostate, were the passing rate was less than 90%, ranging from 58.2% to 84.6%. For the same criterion of 1%/1mm, when accounting for all voxels in the patient receiving at least 10% of the mean target dose (6^th column of table 2a), the passing rate was higher but still below 90% for 3 out of 4 prostate cases. The seventh column in table 2a lists the minimum passing rate among single beams of the plan, for the 1%/1mm gamma criterion for voxels receiving at least 10% of the mean target dose. For most cases these passing rates, although still clinically acceptable, were smaller compared to corresponding results for the full plan (sixth column of table 2a). Prostate cases showed a different trend and the passing rate of the gamma index for 1%/1mm criterion was higher for the individual beams compared to the whole plan, however there were still individual beams with gamma passing rate below 90% for 3 out of 4 patients (Prostate 3 in table 2a).

Table 2a:

Gamma statistics and calculation time analysis per patient. PxDose: Prescription dose in Gy(RBE); V_tar: Total Target Volume (CTV or PTV) in cc; #Beams: Number of beams; V_tar(|γ|<=l, for 1%/1mm): Percentage of target volume passing γ criterion for whole treatment plan; V_tot(|γ|<=l, for 1%/1mm): Percentage of whole dose receiving area passing γ criterion for whole treatment plan; V_tot,min(|γ|<=l, for 1%/1mm): Minimum percentage of whole dose receiving area passing y criterion among individual beams; T_total: Total plan calculation time of whole GPU run (including reading in the phase space files) in seconds per million particles(MP); T_GPU: Total plan calculation time of GPU part of the calculation (without reading in the phase space files) in seconds per million particles; Nprotons: Total number of protons in all phase space files for the complete patient plan run in millions.

Patient	PxDose[Gy(RBE)]	Vtar [CC]	# Beams	Vtar(|γ|<=l) (for 1%/1mm) [%]	Vtot(|γ|<=l) (for 1%/1mm) [%]	Vtot,min(|γ|<=l) (for 1%/1mm) [%]	Ttotal [s/MP]	TGPU [s/MP]	Nprotons[MP]
Lung 1	35	439	2	99.5%	97.4%	96.4%	2.8	1.2	77.4
Lung 2	47.5	114	2	99.8%	99.5%	99.2%	2.5	0.8	31.8
Lung 3	45	186	5	100.0%	99.8%	99.4%	2.9	1.3	155.4
Lung 4	75	132	3	99.8%	97.9%	96.8%	3.2	1.5	50.4
Breast 1	50.4	1274	9	99.4%	99.6%	97.4%	2.7	1.2	463.5
Breast 2	50.4	894	5	99.5%	99.7%	99.0%	2.3	0.7	215.0
Breast 3	50	761	4	98.9%	99.3%	98.8%	2.2	0.7	164.0
Breast 4	50.4	813	7	99.4%	99.7%	98.0%	2.3	0.8	273.6
Breast 5	45	904	5	99.6%	99.7%	97.8%	2.7	1.2	172.7
Breast 6	50.4	358	2	99.0%	99.6%	99.7%	2.3	0.7	61.4
Breast 7	45	824	5	99.6%	99.7%	98.3%	2.2	0.7	215.4
HeadNeck 1	60	89	7	100.0%	99.7%	98.7%	2.9	1.0	77.4
HeadNeck 2	60	51	6	99.9%	98.5%	98.0%	2.6	1.0	91.6
HeadNeck 3	60	50	3	99.6%	99.9%	99.3%	2.6	0.6	23.3
HeadNeck 4	60	22	7	100.0%	99.9%	99.6%	2.8	1.0	93.9
HeadNeck 5	54	128	12	99.9%	99.3%	98.2%	2.9	1.3	267.7
HeadNeck 6	60	100	3	99.2%	99.6%	99.1%	2.2	0.5	36.5
HeadNeck 7	60	87	6	99.9%	99.8%	99.3%	2.6	0.9	51.5
HeadNeck 8	60	134	6	99.9%	99.9%	99.0%	2.8	1.0	53.7
HeadNeck 9	66	68	13	100.0%	100.0%	99.2%	2.9	0.8	95.0
HeadNeck 10	66	86	10	100.0%	97.7%	97.3%	2.8	1.1	125.3
HeadNeck 11	76	38	6	100.0%	99.7%	99.2%	2.7	1.0	55.7
Liver 1	7.74	150	2	99.0%	93.9%	92.3%	2.8	1.1	44.6
Liver 2	58.05	139	2	96.9%	93.4%	93.6%	2.5	0.9	44.6
Liver 3	58.05	176	2	99.2%	97.9%	97.1%	2.7	1.1	46.2
Liver 4	52.5	459	2	98.6%	99.4%	97.2%	2.4	0.8	51.5
Prostate 1	45/77	142/124	4	79.1%/76.5%	87.9%	89.9%	2.9	1.4	240.7
Prostate 2	34	66	2	84.8%	89.6%	91.3%	2.8	1.3	83.1
Prostate 3	50/78	149/178	6	58.2%/64.2%	86.6%	88.1%	3.0	1.5	451.4
Prostate 4	45/79	146/128	4	63.4%/66.6%	87.7%	89.2%	3.0	1.5	290.3

Table 2b:

Patient	PxDose [Gy(RBE)]	Vtar [CC]	# Beams	Vtar(|γ|<=l) (for 2%/1mm) [%]	Vtot(|γ|<=l) (for 2%/1mm) [%]
Prostate 1	45/77	142/124	99.8%	94.8%	96.1%
Prostate 2	34	66	99.8%	95.6%	96.4%
Prostate 3	50/78	149/178	99.8%	94.6%	95.6%
Prostate 4	45/79	146/128	99.7%	94.8%	95.5%

For the prostate cases the failing gamma analysis with 1%/1mm criterion is attributed to the systematic dose differences of 1–2% shown by the dosimetric analysis (section 3.1). To verify this assumption, the gamma distributions and statistics were re-calculated using a more relaxed criterion of 2%/1mm. These results are listed in table 2b, where clinically acceptable passing rates for all cases were observed, both for individual beams and the full plans with a minimum passing rate of 94.6%. If we use a 2%/2mm criterion, the minimum passing percentage is 99.5% for the target volume and 99% for the entire patient for all patients except prostate patients, where the minimum value is 97%.

The eighth column on table 2a shows the total calculation time for the whole patient plan (T_total) in seconds per million particles (s/MP) for the GPU-based calculation, for the full calculation code, including the time spent to tread-in the phase space file data and transfer it to the CPU. Full code calculation times ranges from 2.2 to 3.2 s/MP. Time spent for the GPU calculation part only of the gPMC code (T_GPU in Table 2a) was less than half the full code calculation time, ranging from 0.5 to 1.5 s/MP. The last column in Table 2a shows the total number of protons simulated for the complete patient plan. Accounting for the full simulation time and the total number of protons per plan, average time of less than 2 minutes per beam was observed for all cases except for prostate where the total time was relatively higher but still less than 4 minutes per beam.

4. Discussion

Very good agreement between the two MC calculation methods was observed for the majority of the patient cases. For 23 out of 30 clinical cases all dosimetric indices calculated for the target volumes and full treatment plans by the gPMC method agreed with the corresponding TOPAS results within ±1%. Mean, median dose, D₉₈ and D₀₂ as calculated by gPMC agreed with TOPAS within 2% for the entire patient cohort. Results for all prostate cases showed systematic 1%−2% lower target dose for the gPMC calculation method compared to the TOPAS calculations as shown by the observed differences in mean dose, D₅₀, D₉₈ and D₀₂ in figure 2 for this treatment site.

A similar pattern was observed in the gamma index analysis results, where a criterion of 1%/1mm resulted in clinically acceptable passing rates for individual beams and whole treatment plans for all patient cases except for the prostate patients. Failing gamma index analysis for 1%/1mm criterion for the prostate cases were consistent with the systematic target dose underestimation of 1–2% by the gPMC code, as mentioned above. For these cases clinically acceptable passing rates of the gamma index were achieved for all individual beam and combined plans when a slightly less stringent gamma criterion of 2%/1mm was used, which is still within clinically acceptable dose discrepancies of 2%.

The higher discrepancies observed for the prostate site can be attributed to the higher range used for these cases (Table 1). In gPMC, simulations of nuclear interactions were performed via an approach developed by Fippel et. al. (Fippel and Soukup 2004). Particularly for the inelastic interaction channel, secondary particles were generated through an empirical model. In addition, the cross section data for nuclear interaction channels in gPMC is also from Fippel’s fitted formula, which are likely different from those in TOPAS. The approximations and discrepancy in data yield slightly different dose distributions from the ground truth results in TOPAS. The impacts become more profound in cases with long proton ranges, where dose contributions from nuclear interaction channels are relatively large. We have investigated this issue in cases where a monoenergetic proton beam normally impinges to a homogeneous water phantom. When only electromagnetic channel was considered, dose distributions in TOPAS and in gPMC agree well within MC statistical uncertainty, regardless the proton beam energy. However, when nuclear interactions were turned on, while doses in TOPAS and in gPMC are still in good agreement for a low energy case (100MeV proton beam), discrepancy of the order of ~1% appears for a high energy case (200MeV proton beam). These observations are consistent with results in patient cases. About 1% of protons experience nuclear interactions per cm inside a patient. Thus, for prostate cases for example, even a small difference in nuclear modeling can result in considerable difference at the target, due to the long-range proton beams used for these cases (~25cm).

Figure 3 shows the dose comparison for a single beam for a representative prostate case. Top figure displays the dose difference (gPMC calculation minus the TOPAS calculation) emphasizing that a significance portion of the target volume receives less than 2% lower dose (purple areas). A significant dose difference is also located at the end of range area (left of the target) due to the difference in the range predicted by the two calculation methods. This range difference is smaller than 1 mm, as it can be shown by the gamma distribution using 1%/1mm criterion (figure 3 bottom), in which the area at the end of range passes the gamma criterion (absolute gamma value of less than 1). Larger discrepancies are observed at the entrance region and inside the target. More specifically we observe a sloped dose distribution within the patient, having higher doses at the entrance region and lower inside the target. Since we normalize the results of both calculation methods in the same way, assigning the prescription dose to the center of the SOBP, this slope in the dose presents as an overestimation of the dose at the entrance region and an underestimation at the distal end, keeping the integral dose the same. We are currently in the process of implementing an updated model of the nuclear interactions in gPMC to resolve these discrepancies. It will be included in the next version of the code.

Figure 3:

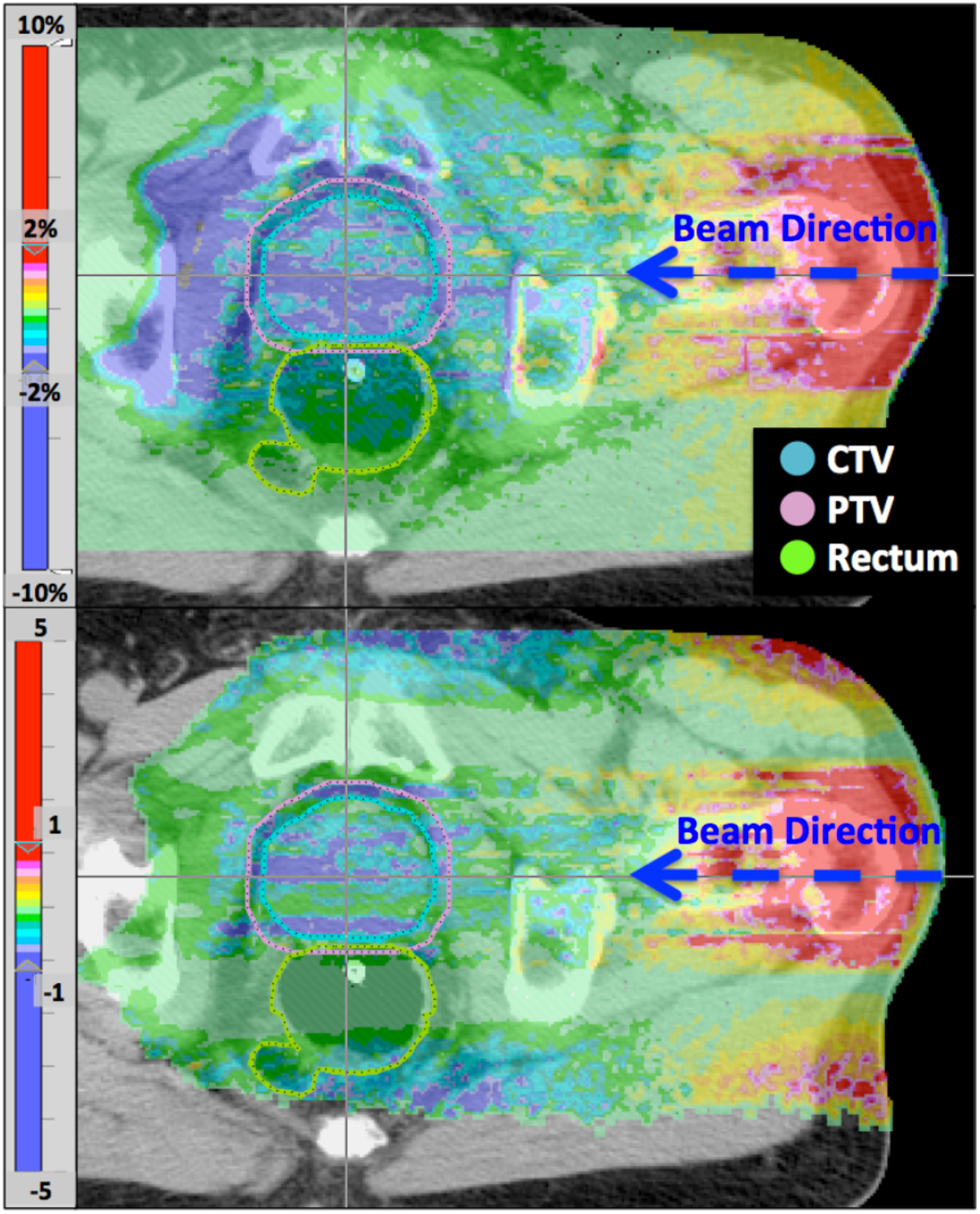
Dose difference (top) and gamma distribution (bottom) of a single beam from a prostate plan. Top colorbar is in percent of prescription dose for this beam.

Overall a very good agreement was observed between the GPU-based and the full MC codes. To estimate the statistical uncertainty in the gPMC calculations, the standard deviation of the scored dose per voxel was recorded. The mean standard deviation among all voxels receiving at least 30% of the prescription dose per beam ranged from 0.5% to 2.4%, which is comparable to the 1–2% estimated uncertainty in dose calculation by TOPAS. The exact uncertainty value depends mainly on the number of particles in the phase space file and the treatment site. Head-and-neck cases showed the highest statistical uncertainty, especially for individual beams covering smaller target areas for which the number of protons in the phase space file after the aperture was relatively small.

The calculation time for the gPMC code is just a small fraction of the corresponding time for TOPAS calculation, when using the same initial number of particles. As an a example, for a typical head-and-neck case, the gPMC calculation time is 2.6 seconds per million particles on a NVIDIA TESLA C2075 card versus 4 hours per million particles for TOPAS calculation on a 2.8–2.9GHz Intel X5600 CPU. We should keep in mind, however, that gPMC is a proton therapy dose calculation code optimized for speed, whereas TOPAS is a versatile particle simulation toolkit, not optimized for speed accordingly. Almost half of the total GPU-based calculation time is spent on data communication between the GPU and hard drive and thus it can be greatly reduced if more efficient data transfer processes are implemented. Keeping the data in the main memory and then initializing the GPU processing could potentially reduce the time needed for data transfer. However in our current implementation we were not able to keep the data in CPU memory, since TOPAS, which generated the phase-space files at the end of the treatment nozzle, and gPMC were run on different computer systems.

Both processing times include reading-in the phase space file at the exit of the treatment head and calculating the dose within the patient CT. For passive scattering treatment, the first part of the calculation, simulating the treatment head including the patient specific aperture and compensator, is performed by TOPAS for both calculation methods and is not accounted in the total calculation time reported in this study. This calculation method, starting from a phase space file at the exit of the treatment head, is a scenario applicable to Monte Carlo simulation for pencil beam scanning (PBS) dose calculation where beam models instead of patient specific treatment head geometries can be used. Excellent calculation accuracy and minimal calculation times show the potential of gPMC to be used in inverse and even adaptive treatment planning for proton therapy.