All-atom adaptively biased path optimization of Src kinase conformational inactivation: Switched electrostatic network in the concerted motion of $\mathbf{\alpha }$C helix and the activation loop

Abstract

A method to optimize a conformational pathway through a space of well-chosen reduced variables is employed to advance our understanding of protein conformational equilibrium. The adaptively biased path optimization strategy utilizes unrestricted, enhanced sampling in the region of a path in the reduced-variable space to identify a broad path between two stable end-states. Application to the inactivation transition of the Src tyrosine kinase catalytic domain reveals new insight into this well studied conformational equilibrium. The mechanistic description gained from identifying the motions and structural features along the path includes details of the switched electrostatic network found to underpin the transition. The free energy barrier along the path results from rotation of a helix, αC, that is tightly correlated with motions in the activation loop (A-loop) as well as distal regions in the C-lobe. Path profiles of the reduced variables clearly demonstrate the strongly correlated motions. The exchange of electrostatic interactions among residues in the network is key to these interdependent motions. In addition, the increased resolution from an all-atom model in defining the path shows multiple components for the A-loop motion and that different parts of the A-loop contribute throughout the length of the path.

I. INTRODUCTION

Conformational flexibility of protein molecules has long been recognized as essential for biological function, but our understanding of the relationship between the function and the conformational landscape is far from complete. While experiments provide essential information about some of the features of the landscape (static structures and rate constants), computer simulations are needed to achieve the atomistic details of protein conformational ensembles required for mechanistic understanding. With the development of powerful methodologies, including Markov State modeling (MSM),^1,2 and the enormous increase in computational power, considerable headway is being made toward computationally mapping protein conformational landscapes and relating their features to the function. With greater computational capacity through algorithmic and hardware advancements, straightforward sampling and enhanced sampling methods have extended molecular dynamics (MD) timescales to hundreds of microseconds and even milliseconds for a limited number of cases.^3–5 Nevertheless, the resources for computing on these timescales are limited and not generally available. Furthermore, many important biological processes occur on timescales that remain beyond what is achievable with extensive sampling and state-of-the-art MSM. Path-directed methods offer a complementary approach to extensive sampling of the conformational landscape.⁶ An example is a recent proposal that explicitly combines the minimum-free-energy path (MFEP) method with MSM in a hierarchical scheme to enable investigating transitions with timescales exceeding that of simulations.⁷ By their nature of utilizing a reduced set of variables to define a transition path between two stable end-states, path-directed methods have faster convergence in sampling than that required by MSM. While the dependence of the path on the selected variables makes the choice of variables a critical step, a well-chosen set can define a path that approaches the transitions that occur spontaneously in unbiased MD simulations.⁸ A mechanistic description of the transition process between the reactant and product is a direct outcome of path-directed methods without the need to extract this information from a broad conformational landscape. Finally, once a path is defined, images extracted along the path are useful as starting coordinates to initiate multiple MD simulations focused on the region of interest for the extensive sampling needed to construct MSMs⁹ when detailed information on microstates and transition probabilities is desired.

We present here the application of a path-sampling strategy, adaptively biased path optimization (ABPO),¹⁰ which seeks to define a conformational transition between two known end-states by optimization of a path through a reduced-variable space.¹⁰ The free energy along the path is an immediate result. ABPO and two other strategies^11,12 differ from most path-sampling methods by allowing the system to explore the region of the path in contrast to restraining the system to the path in the fashion of a “chain-of-states.” A complete description of the ABPO method is published.¹⁰ Briefly, ABPO is an optimization scheme to converge a path to the principal curve for the transition, where the principal curve runs through a single reaction channel that connects two stable states on a free energy landscape. ABPO utilizes the path description of the finite-temperature string method^13,14 and defines the path in terms of the mean position in hyperplanes orthogonal to the tangent at each point of the path. The ABPO scheme updates the path to the mean position of trajectories that freely sample the path to converge to the principal curve and compute the potential of mean force (PMF) along that curve. The path is constructed in a reduced dimensionality space, a key simplification for the computation of a PMF along the path.¹⁵ An adaptive biasing potential constructed from the sampling history¹⁶ accelerates sampling along the path in molecular dynamics simulations to efficiently evolve the path. An important feature of the method is that the sampling is not restrained to the path, and only a “tube” potential is used to focus on conformational configurations within a given radius of the path.¹⁰ The tube potential enables efficient sampling while allowing a certain breadth of conformations along the path. Given that the target objective is specifying the principal curve, ABPO affords efficient sampling that will not be trapped by a rugged free energy landscape. The computation is initiated from multiple trajectories launched from the two known stable end-states without the need to generate starting, often unphysical, structures built at intervals along the initial path, which is a necessary component of path-restrained search algorithms. ABPO was first applied using a coarse-grained Gō-model to obtain a path for a conformational transition of the Lyn kinase domain^10,17 and later with an all-atom model to study simple motions for short-loop closures and a rigid-body helix flip movement in three proteins.¹⁸ ABPO was shown to efficiently converge the path to the principal curve, defining an optimal transition path in these systems. Comparison in one case of ABPO with the maximum flux path approach, which is similar to the string method, found ABPO to be twice as fast to reach convergence, a result attributed to the need to equilibrate structures as part of the protocol in path-restrained approaches.¹⁰ Here, we apply ABPO using an all-atom model of the Src kinase domain to compute the conformational transition.

Protein kinases (PKs), particularly the Src-family kinases, have become an archetypical computational system for exploring conformational landscapes and complex structural transitions. The keen interest in PKs derives partly from their central role in human disease; PKs regulate essential intracellular and intercellular signal transduction pathways, including cell migration, cell cycle, and survival,^19,20 and dysregulation of the kinase activity often leads to aberrant signaling pathways causing cancer, diabetes, or inflammation.^21,22 Indeed, PKs are the second largest protein family targeted for drug design.²³ Computational interest also stems from the fact that most protein kinases with published crystal structures are known to exist in multiple forms, generally considered to be either catalytically active or a down-regulated, inactive structure. A number of structural features distinguish active and inactive states, and this rich complexity of conformational flexibility and manifold in states, not amenable to harmonic-type analysis, has attracted computational efforts from many fronts.

The transition between active and inactive forms of Lyn, a Src-family kinase, was among the first for computational analysis by nonequilibrium methods.^24,25 Recent studies of the Src transition exploiting the enormous increase in current computational power include the use of extensive MD and MSM,^9,26–28 coupled with enhanced sampling methods such as metadynamics,²⁹ pH tempering,³⁰ or biased sampling methods.³¹

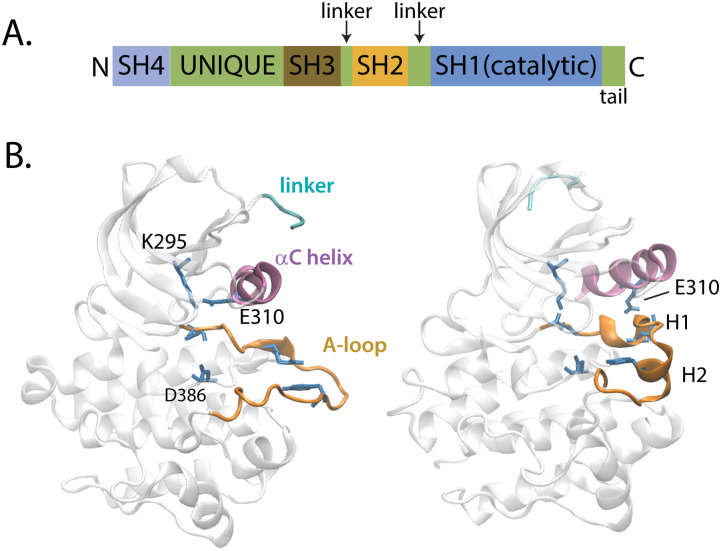
Src tyrosine kinase comprises three folded domains connected by linkers [Fig. 1(a)]. The kinase catalytic domain (CD), with ∼270 residues, contains all that is needed for catalytic transfer of a phosphoryl group from ATP to a substrate tyrosine. The two smaller regulatory domains (SH3 and SH2) are for cellular localization mediated through protein–protein interactions and a unique/SH4 region for anchoring to the plasma membrane. Here, the interest lies in the isolated Src CD [Fig. 1(b)], which undergoes the conformational activation process associated with regulation of enzymatic activity. The CD has a smaller N-lobe with a five-stranded β-sheet and αC helix and a larger C-lobe mostly with a helical structure. The activation loop [orange in Fig. 1(b)], A-loop, is part of the C-lobe and lies at the interface with the N-lobe. Phosphorylation on the A-loop is part of the tight regulation of Src catalytic activity. By examining the unphosphorylated Src CD system (residues 255–521, chicken c-Src numbering), we investigate the state of Src in which the domains are disassembled and the A-loop available for phosphorylation.

FIG. 1.

Src structure. (a) Linear domain structure of Src-family kinases. Folded domains include the large catalytic, or kinase domain, and smaller regulatory SH2 and SH3 domains. (b) The Src catalytic domain, SH1, used for the ABPO computation (residues L255–T521) shown in the activated form (left, PDB entry 1Y57) and the inactive form (right, PDB entry 2SRC). Structural differences include the rotational orientation of the αC helix (pink, residues 304–316), the internal structure of the A-loop (orange, residues 404–424), and the linker residues 255–260 (cyan) that connect the kinase domain to the SH2 domain. Key residues described in the text are shown in stick representation.

Crystallography has revealed the disparate downregulated and activated forms of the kinase domain structures [Fig. 1(b)]. The major structural differences between the downregulated (PDB entry 2SRC³²) and activated (PDB entry 1Y57³³) crystallographic structures are as follows: (1) the αC-helix is rotated either out or in as indicated with the position of the E310 sidechain, (2) the A-loop conformation is either folded in or extended outward, and (3) the relative position of the N-lobe and C-lobe is either closed or open. In the downregulated form, the folded-in A-loop has two single-turn helices, H1 and H2, that lie between the N-lobe and the C-lobe, preventing access to the catalytic site. In the activated form, the extended A-loop is displaced from the catalytic site allowing access to the catalytic residue D386. The αC-helix orientation affects catalysis by altering the position of E310, whose catalytic role is to stabilize the position of ATP. In the activated form, the αC helix rotates ∼25° from the downregulated form to bring E310 in close contact with K295 to form a catalytically important salt bridge.³⁴ The opening between the N-lobe and C-lobe at the catalytic site increases in the activated form to accommodate the inwardly rotated αC helix. While crystallography defines the stable structural states of Src, it is clear from nuclear magnetic resonance (NMR) that the Src CD is a highly dynamic and mobile protein.^29,35–37

Our investigation of the Src CD inactivation process using the path-sampling strategy of all-atom ABPO has yielded new information on the transition. The role of the previously recognized electrostatic network involved in the transition process is illuminated with a description of the exchange between electrostatic residue interactions along the path. The exchange of residue partners underpins the coupled motion of the A-loop with the rotation of the αC helix that contributes to the free energy barrier. In addition, the A-loop motion is complex, with different regions of the loop changing throughout the transition path.

II. RESULTS

A. Reduced variable selection and evolving the path

An initial step of transition-path optimization methods is the selection of the reduced set of geometric descriptors that define the search space and the path. A well-chosen set that captures the structural changes necessary and sufficient for the transition can enable an accurate description of the path using enhanced sampling of path-directed methods. The importance of identifying an appropriate variable set was illustrated by comparison of paths from enhanced sampling to paths obtained from unbiased simulations.⁸ We use the term “reduced variable” (RV) here in preference to the commonly used term “collective variable” because the variables chosen are not generally descriptors of a correlated motion. The ABPO protocol implemented in the Chemistry at Harvard Molecular Mechanics (CHARMM) program evolves the path in cycles, including a path optimization step at the end of each cycle. The path is described in terms of hyperplanes orthogonal to the path¹³ and is updated to the mean position in the hyperplanes based on the combined adaptive sampling of multiple trajectories for the cycle. Enhanced sampling of the path is achieved with the gradient resulting from an added bias potential, V_b, at point λ in the reduced variable space on the path,¹⁰

$$V_b\left(\lambda ,t\right)=k_{B}T\frac{b}{1-b}\text{ln}\left[c\left(1-b\right)h\left(\lambda ,t\right)+1\right],$$ (1)

where the histogram h(λ,t) counts visits to the region λ over time t, b is the fraction of the free energy flattened by the bias, c has inverse time units and controls how the bias couple to the dynamics, k_B is the Boltzmann constant, and T is the temperature. The system is not restrained to the path coordinates, but sampling is held to the region of the path with a tube potential of specified diameter, here set to 20 Å.

The evolution of the RV as a function of the path with each cycle is convenient to assess the effectiveness of a particular RV to promote the system progress along the path,¹⁸ as well as to follow convergence to the optimal path. The geometric descriptors considered here are internal distances and torsion angles from regions of the protein with substantial structural differences. The complexity of the conformational transition of Src CD (residues L251 to T521) is greater than previous transitions evaluated with all-atom protein models and ABPO,¹⁸ requiring assessment of several sets of RVs to find an optimum path for Src inactivation. Transitioning from the active to inactive conformation, the A-loop structure changes from an outwardly extended loop to a folded-in, two-helical structure [Fig. 1(b)], and most of the main chain torsion angles vary during this process. As torsion-angle motions are the basis of conformational fluctuations of molecules and a natural choice for RVs, we first considered for RVs a linear combination of torsion angles. Torsion-angle based RVs successfully promoted an open/closed transition of a short loop in the protein dihydrofolate reductase.¹⁸ For the Src CD A-loop residues 404–424, the differences in backbone torsion angle values are evident from the (ϕ, ψ) distributions (see Fig. S1 of the supplementary material). We ran ABPO with a combination of distance-based RVs for αC helix rotation and dihedral angle RVs for A-loop folding. Nevertheless, in the simulation, we observed that the torsion angle RVs for the A-loop showed progress with the number of cycles, but visualization of the trajectories determined that the tertiary structure of the polypeptide chain did not change and no transition between the two end-states occurred. We concluded that the flexibility of the loop backbone atoms accommodated the local rotation about the dihedral angle without moving the system between end-states. The lack of sampling along the path suggests that dihedral angle RVs are not good choices for protein folding-like conformational transitions. This example also illustrates the importance of examining structures in addition to monitoring the progress of the reduced variables to gage the quality of sampling directed by a reduced set of conformational coordinates.

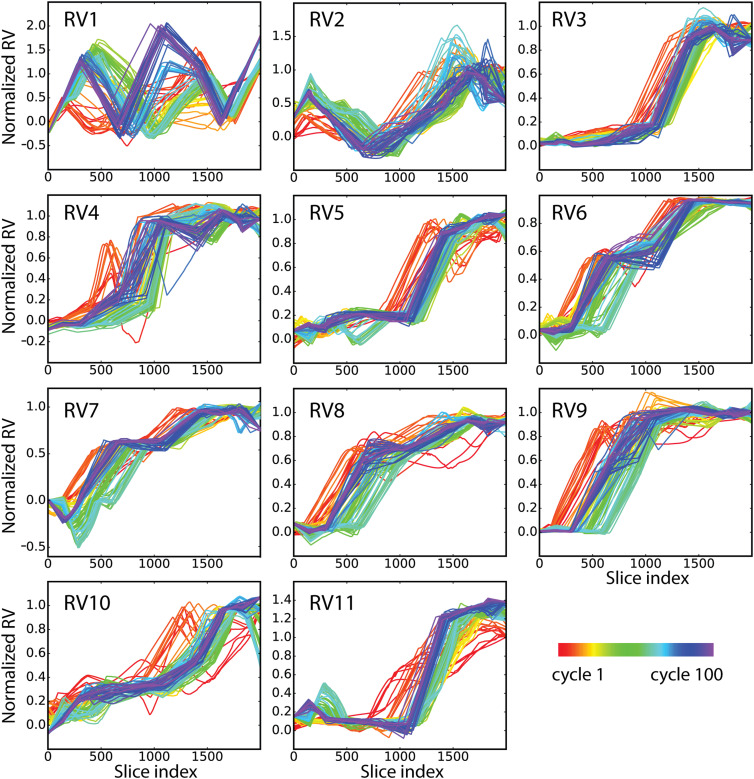
Based on these observations, we turned our focus to RVs that are a linear combination of only internal distances. RVs were defined based on the larger structural differences between active and inactive forms of Src CD. Internal distances were mostly between main chain atoms (Cα-Cα ≥ 2.5 Å), and certain side chain motions were captured with Cα-side chain and side chain–side chain internal distances. The resulting RVs included internal distances for residue pairs with one or both residues being in the αC helix or the A-loop (see Table S2 of the supplementary material). A final group of 11 RVs was defined according to the procedure and criteria detailed in Sec. IV. To examine convergence of the RV profiles, the evolution from the first cycle to the last cycle 100 of the 11 RVs averaged over 16 replicas is shown in Fig. 2, where the normalized RV value is plotted as a function of the path hyperplane specified by a “slice” index. Many RV profiles are converged within ∼70 cycles, and all profiles show reasonable convergence with 100 cycles, except one region of the RV4 profile.

FIG. 2.

RV profiles illustrating convergence of the 11 normalized RVs. Panels (a)–(k): the evolution from cycle 1 (red) to cycle 100 (purple) of a normalized RV as a function of the ABPO transition path between active (RV = 0) and inactive (RV = 1.0) forms of Src CD. The path is discretized into 2000 hyperplanes (slice index). The ordinate is scaled individually for each RV. RV3, RV5, and RV11 profiles exhibit correlated motions starting near index 1100 on the ABPO path.

B. Reduced variable, RV1, of the N-terminal linker residues

Linker residues L255 to W260 at the N-terminus of the Src CD that connect to the SH2 domain were found important for the inactivation transition. We initially truncated full-length Src at residue Trp 260 so that the simulation system for Src CD included residues W260–T521, similar to systems used in several computational studies of Src CD.^9,30,38 Nevertheless, this system was found to be unreliable and difficult to obtain reproducible results (for details, see the supplementary material). It was also determined that including an RV with internal distances between the N-linker residues L255 to W260 and αC helix was needed to achieve a complete path between the known end-states. These results are sensible given that experimental studies determined residues Leu 255 and Trp 260 in the linker separating the SH2 domain and kinase domain of full-length Src play a role in regulating activation of Src-family kinases.^39–42 Computational studies have also examined Trp 260 behavior^24,43,44 and suggest that the role of Trp 260 in regulation is to “lock” the αC helix in the outward form, and the interaction releases upon disassembly of the regulatory domains to allow αC helix to rotate in upon activation.

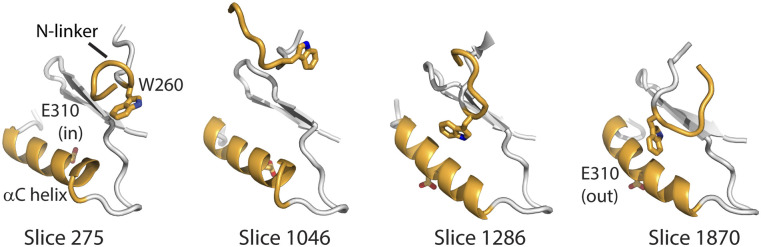
RV1, comprising N-linker to αC helix internal distances (Table S2), displays an unusual profile (Fig. 2). In the optimized ABPO path obtained for Src CD, RV1 does not traverse from 0 to 1 directly, as typically observed, but oscillates over the range ∼0 to ∼2 [Fig. 2(a)]. This RV1 profile can be explained by the nature of the N-linker movement and the relative conformational changes between the N-linker and the αC helix. Visual examination of the structures along the path (Fig. 3) finds that displacement of the N-linker outward from the rest of the Src CD occurs to allow rotation of the αC helix. At the inactive end-state of the ABPO path length, RV1 deviates somewhat from the normalized value 1, which is set from equilibrium MD sampling of this end-state. ABPO does not restrain the path ends, and that the value is not close to 1 likely results because RV1 comprises distances of the flexible N-terminus of the Src CD. The rich variation over the path of RV1 reflects a nonlinear nature in the transition identified with ABPO that perhaps would not be revealed with a path-restrained approach.

FIG. 3.

Structures of the N-terminal linker region highlighting the variation in RV1 along the ABPO path (RV1 profile shown in Fig. 2). W260 in the N-linker and E310 in the αC helix are shown in stick representation. In the active state (slice 275), W260 is distant to the αC helix, which is rotated with E310 positioned inward. In the inactive state (slice 1870), W260 is tucked between the αC helix and a β-strand stabilizing the outward orientation of the αC helix. In an intermediate conformation along the path (slice 1046, RV1 ∼ 2), W260 is positioned outwardly, allowing subsequent rotation of the αC helix indicated by the position of E310.

C. Transition path PMF: The free-energy barrier is $\mathbf{\alpha }$C helix rotation and correlated A-loop motions

The potential of mean force (PMF), A(λ, t), along a path of length Λ parameterized with λ, where 0 ≤ λ ≤ Λ, is computed from the histograms obtained from sampling the optimized ABPO path over time, t,

$$A\left(\lambda ,t\right)=-k_{B}T\frac{1}{1-b}\text{ln}\left[h\left(\lambda ,t\right)/\text{max}\left[h\left(\lambda ,t\right)\right]\right].$$ (2)

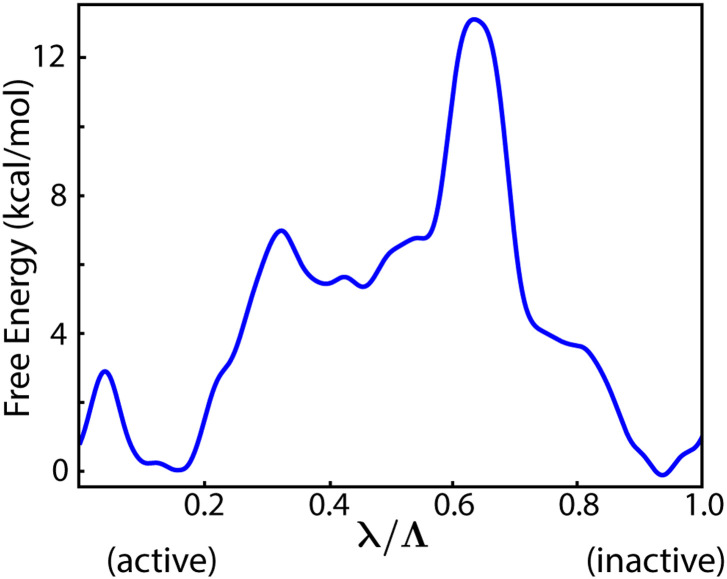
Here, b is the fraction of the free energy canceled by the potential that adaptively biases the dynamics, k_B is the Boltzmann constant, and T is the temperature. The PMF computed for Src CD inactivation along the optimized ABPO path with extended sampling (see Sec. IV) is shown in Fig. 4.

FIG. 4.

PMF of the ABPO path for the Src conformational transition between active and inactive forms. The maximum free energy barrier reflects rotation of the αC helix.

The inactivation-path PMF free-energy (FE) barrier occurs near λ/Λ ≈ 0.64. The ∼12 kcal/mol barrier height is somewhat higher than expected for the timescales estimated by others²⁸ and likely reflects the difficulty of sampling high FE regions of the conformational landscape. In the previous work using a double-basin Gō model,^10,17 the FE barrier is later in the inactivation transition and near the end-state at λ ∼ 0.82. In contrast to the path determined using a coarse-grained model, the ABPO path from an all-atom model reveals higher complexity in the conformational landscape between the FE barrier and the inactive end-state basin (0.64 < λ/Λ < 1). The added complexity not captured with the Gō model is the formation of a short helical structure in the A-loop C-terminus (described below), which may require the side chain interactions missing in the Gō model.

Even though the position of the FE barrier on the path differs, the structural change causing the FE barrier in the all-atom PMF (Fig. 4) is the same as that for the path obtained with the coarse-grained model.¹⁷ Examination of the structures near the FE barrier finds the rotation of the αC helix to be the major change at the high free energy. The αC helix movement was identified to be the primary energetic barrier in the transition of the kinase domains of Src and CDK4 conformational transitions.^10,17 We note that during our assessment of different combinations and numbers of RVs, the highest energy barrier on the path is consistently associated with the rotation of the αC helix, which is similar to the behavior observed previously using a maximum flux approach to define the inactivation transition.¹⁷ Based on analysis of kinase structures in the PDB, this energetic role of αC helix rotation in the transition is suggested to be a kinome-wide property. As such, it provides a rationale for numerous regulatory structures, which is difficult to glean from the static structures alone.

The RV profiles (Fig. 2) give additional insight into conformational changes taking place at the FE barrier. Examination of the RV profiles finds that the converged profiles of RV3, RV5, and RV11 are correlated and change abruptly in the path region of the FE barrier. The RV3, RV5, and RV11 profiles are relatively invariant up to the slice index ≈1100 (λ/Λ = 0.55) and then increase sharply to near their final values at the slice index ≈1400 (λ/Λ = 0.7). The large, correlated change in these RVs encompasses the FE maximum in the PMF (λ/Λ ≈ 0.64). RV3 comprises internal distances of the αC helix with the N-lobe and A-loop (see Table S2 of the supplementary material) and therefore describes rotation of the helix. RV5 captures motions within the A-loop and RV11 captures the relative movement of the A-loop with the C-lobe. The correlated motions associated with the FE barrier provide a description of the inactivation transition as an interdependence of αC-helix rotation with the A-loop motion between extended and folded-in forms. The nature of these two structural features requires that residues more than 20 Å apart are coupled during the conformational transition. The early work on Src family kinases using non-equilibrium methods recognized that these two motions must be concerted due to the contact between the αC helix and the A-loop and the steric conflicts that would occur if the motions were independent.²⁵ Correlated motions of residue groups in the Src kinase domain have been observed in previous computational simulations.^9,36

The active and inactive ensembles are observed from the path PMF in Fig. 4 to have nearly equivalent free energy. Previous investigations of the conformational transition for Src CD using umbrella sampling^31,44 or Markov state modeling²⁶ and of the Src family as a whole²⁸ found that the inactive state is favored by 1 kcal/mol–5 kcal/mol. The ABPO results are therefore consistent with the lower end of this range.³⁷

D. Switched electrostatic network

A switched electrostatic network (SEN) was detected in early computational studies of Lyn kinase conformational activation using nonequilibrium methods.^24,25 A network of electrostatic residues was observed to switch from a set of interactions in the active end-state [Fig. 5(a); E310–K295 and R409–Y416] to an alternative set in the second end-state [Fig. 5(c); E310–R409 and Y416–D386]. The key finding was that the change from one electrostatic pair to the second pair occurred during the transition with no intermediate condition of breaking one pair without forming the alternative pair. This direct hand-off of partners was suggested to be energetically favorable by suppressing possible off-pathway intermediates that could slow the transition. There is experimental support that the SEN contributes to the Src transition,²⁴ and the participation of the electrostatic network has emerged in other computational analysis.^31,44–46 Because the SEN residues are in the A-loop and aC helix, their behavior along the transition path provides additional insight into the correlated motion of these two structural features.

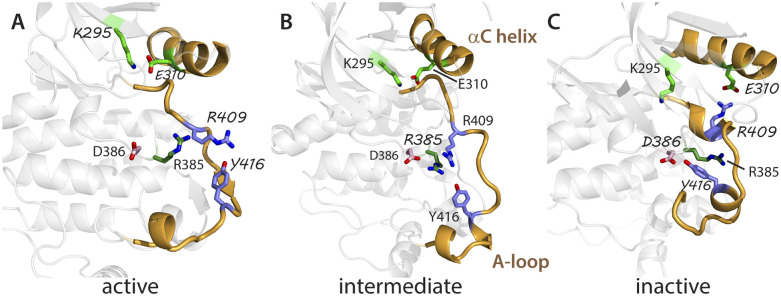
FIG. 5.

The switched electrostatic network (SEN) of SrcCD (ribbon) with different electrostatic pairs (residues in stick representation) illustrated with structures for (a) the stable active form, (b) an intermediate on the inactivation path prior to αC helix rotation, and (c) the stable inactive form. Highlighted interactions are indicated with different fonts. The pairs in the active state are K295–E310 (green) and R409–Y416 (slate), which switch to E310–R409 and Y416–D386 (pink). In switching from R409 to D386, Y416 interacts favorably with R385 (forest) of the HRD motif in an escort-manner over nearly the full path length to stabilize transition of the A-loop between the extended and folded-in conformations. The αC helix and A-loop are highlighted in gold.

We examined the SEN interactions over the path determined using the all-atom model ABPO approach, which should yield a more accurate description of the transition path than the nonequilibrium method. Inter-residue distance distributions specified in terms of a coarse binning of the path were computed to characterize the interaction of residue pairs in the electrostatic network. Inter-residue distances for SEN residue pairs and the corresponding slice index were determined for each frame of the path-optimization trajectories. The path was coarsely divided into ten bins, giving a bin width of 0.1 λ/Λ, or 200 slices. The resulting inter-residue distance distributions along the path are shown for the SEN pairs in Fig. 6.

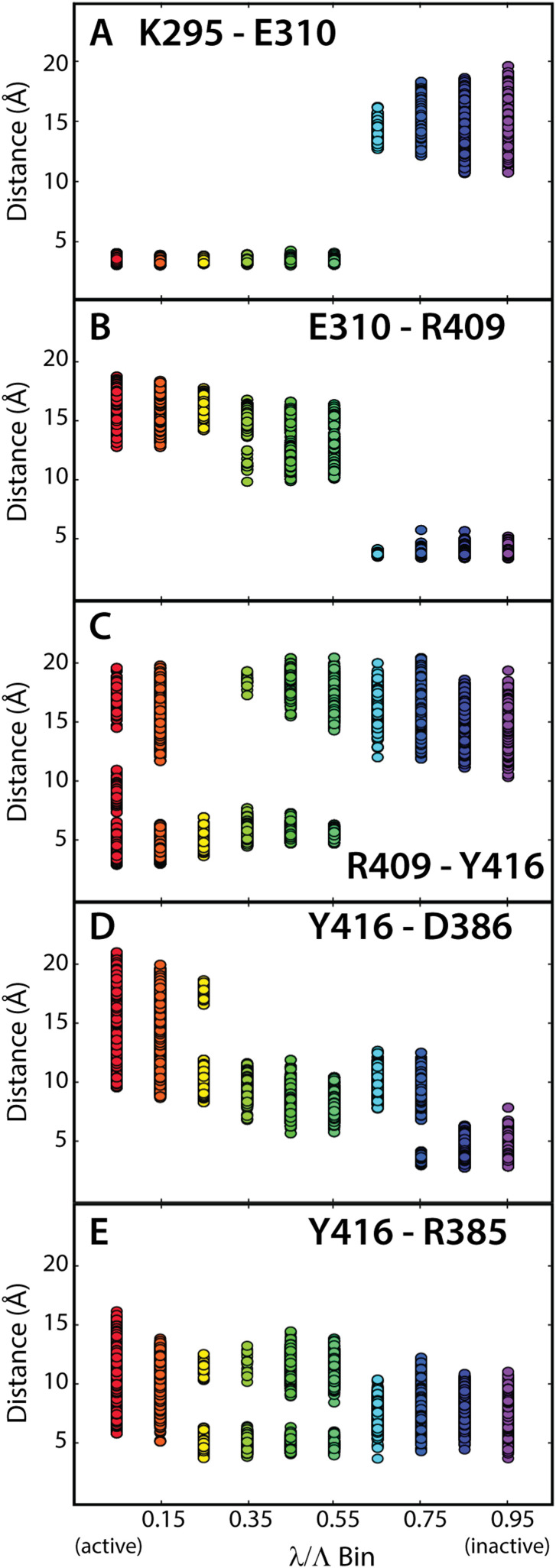
FIG. 6.

Inter-residue distance distributions of the SEN electrostatic residue pairs as a function of the path length. Distances between polar groups of the indicated side chains are binned in 0.1 increments of the ABPO path index λ/Λ and shown with the rainbow color scale from 0 to 1. SEN residues switch from one salt-bridge partner directly to another during the transition. E310 in the αC helix switches between K295 [panel (a)] and R409 [panel (b)]. R409 switches between Y416 in the A-loop [panel (c)] and E310. Y416 switches between R409 and D386 [panel (d)]. The transition of the A-loop is further affected by interaction of Y416 and R385 that occurs transiently throughout the transition [panel (e)]. R385 and D386 are residues of the HRD motif on the catalytic loop. Distances are between sidechain atoms: Cγ for Asp, Cδ for Glu, Nζ for Lys, Cζ for Arg, and Oη for Tyr.

The pattern of the path-dependent distributions in Fig. 6 shows the expected SEN behavior for the all-atom ABPO path. An SEN switch is characterized from two distributions of a central residue, i.e., two panels in Fig. 6 with a common residue E310, R409, or Y416; one distribution with short distances at small λ values switches to longer distances at larger λ concomitant with the switch to shorter distances for the alternate SEN partner shown in the second panel. E310 manifests clear switch behavior by having a short-distance interaction with K295, which at λ/Λ ≈ 0.6 is lost concomitant with gaining a strong interaction with its alternative partner R409 [Figs. 6(a) and 6(b)]. The sharp hand-off between two binding partners for E310 derives from αC helix rotation. In the inactivation transition, R409 switches to E310 from its interaction with Y416 [Fig. 6(c)]. The R409–Y416 distribution does not show as distinct a switching behavior in that the loss of this interaction takes place over nearly one third of the path or three bins. A broad switching also occurs for the part of the Y416 switch changing to interact strongly with D386 [Fig. 6(d)]; in this arm of the Y416 switch, the exchange occurs continuously over the full path. Figure 6(e) shows the distribution for the pair Y416–R385. The original SEN description²⁵ did not include R385, but analysis of the all-atom ABPO path discovered that Y416 closely associates with R385 as well as with R409 and D386 identified in the original SEN. An intermediate conformation on the path illustrates the favorable Y416–R385 association [Fig. 5(b)]. R385 and D386 are part of the conserved amino-acid sequence motif, HRD, in the catalytic loop of PKs, while R409 and Y416 are on the A-loop. Together, the orchestrated interactions of R409, D386, and R385 act as escort for Y416 between the end-states. The importance of the HRD motif to the A-loop dynamics and activation has been recognized,⁴⁷ and this new insight of its role in the conformational transition adds to that understanding. The continuous nature of the exchange in Figs. 6(d) and 6(e) arises from the internal mobility of two interacting side chains anchored to the ∼20-residue-long A-loop.

E. Activation loop motion contributes to the full path

To visualize the transition from the active to the inactive forms of Src CD, a path was constructed from the ABPO trajectories sampling the optimized path. Frames were extracted from the trajectories according to the hyperplane associated with the coordinates. The series shown in Fig. 7 illustrates conformational characteristics of the transition events along the path.

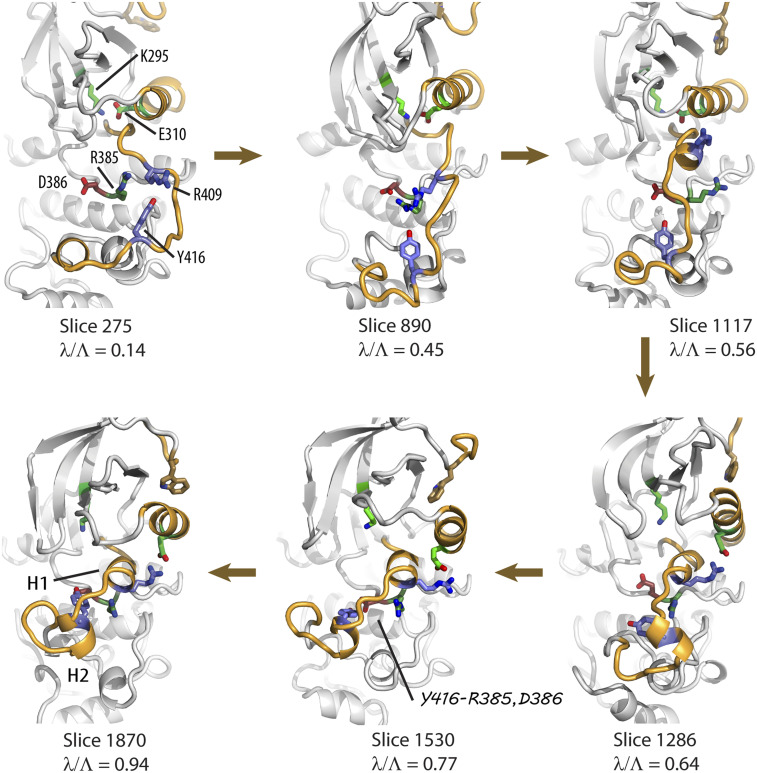
FIG. 7.

Representative structures along the inactivation path showing some of the key steps in the transition process. The αC helix, the A-loop, and the N-terminal linker are in gold. The SEN residues (K295, E310, R409, Y416, R385, and D386) are shown in stick representation and colored as in Fig. 5. W260 in the N-linker is in gold. The A-loop motion occurs along the full path, moving from the outward, activated form (λ/Λ = 0.14), crossing below αC helix as viewed (λ/Λ = 0.56), and then folding over the catalytic site (λ/Λ = 0.77) with the final docking of the short H2 helix (λ/Λ = 0.94).

The A-loop motions going between the extended (active) and the folded-in (inactive) forms are complex such that different regions of this 20-residue loop (residues D404–F424) vary in conformation over the full length of the transition path. The extended A-loop in active Src CD lies along the surface of the C-lobe helical core crossing below αC helix, as shown in Fig. 7 (λ/Λ = 0.14). In the inactive Src CD end-state (λ/Λ = 0.94), the folded A-loop conformation comprises two short helices, the first, H1, at its N-terminal end (residues G406–L410) and the second, H2, is midway in the loop (residues N414–A418) and covers the catalytic site. Early in the transition from the active state, the A-loop moves toward the catalytic site (right to left in Fig. 7), still in an extended conformation but with internal conformational variations (λ/Λ = 0.45). This motion is captured with RV6, RV7, RV8, and RV9 (Fig. 2). Approaching the FE maximum, H1 residues at the N-terminal region of the A-loop take on a helical propensity (λ/Λ = 0.56) captured with the RV4 prior to rotation of the αC helix (E310 is still “in”). At the FE maximum (λ/Λ = 0.64), rotation of the αC helix occurs over a short path length and H2 residues midway in the A-loop adopt a helical structure, but this short helix is not yet positioned relative to the catalytic site as in the stable end-state. This path region shown for λ/Λ = 0.56 and 0.64 is that of the correlated changes in the RV3, RV5, and RV11 profiles described above. Along the path following the FE maximum (λ/Λ = 0.77) is motion of the H2 helix relative to the C-lobe that is directed toward its position covering the catalytic site in the stable inactive conformation (λ/Λ = 0.94). The SEN pairs Y416–R385 and Y416–D386 form stabilizing interactions in the latter part of the inactivation path. The low-resolution description of the path obtained with the Gō model, starting from the active-state basin to the FE maximum, is consistent with the all-atom optimized path presented here,^10,17 except that the later stage of inactivation to dock the H2 helix deep in the catalytic site region was not reproduced with the Gō model. The two ABPO paths both identify extensive interactions along the path between the A-loop and αC helix requiring their motions to be interdependent.^25,46 In addition, we note that the ABPO path here appears consistent with transition paths generated from the string method³⁸ and enhanced-sampling schemes,^31,46 as well as the path constructed from Markovian microstates.^9,26 Specifically, some previous studies describe the path in terms of distances related to E310 for rotation of the αC helix and distances that report on the helical structure of H2 in the A-loop for folding of the A-loop. Thus, the A-loop motion is followed using a descriptor localized to the H2 helical formation. The sequence of events for inactivation is reported to be αC helix rotation then A-loop folding, which is measured from H2 formation.^9,26,31,38 The all-atom ABPO inactivation path shows that both of these events occur near the maximum FE barrier, with other structural changes in the A-loop preceding and subsequent to this barrier.

III. CONCLUSIONS

In this study, we used ABPO, an unrestrained computational approach to identify a transition path between conformationally disparate end-states of the protein Src tyrosine kinase. An optimized path, specified in terms of a set of reduced variables, is obtained from the adaptively biased dynamics that enhances sampling in a tube region of the path. Extended, unrestricted sampling in the tube of the optimal converged path yields information on the set of conformations along the path, in contrast to a transition path characterized with conformations tied to the path. In the study here, the free sampling of ABPO in the tube region evolved a path that included a range of motions for the N-terminal linker residues, which may not have been detected with path-restricted methods. A limitation of the biased sampling of ABPO observed in this study is the potential of insufficient sampling of high free-energy regions of the reduced variable space within the available computer time so that high free-energy barriers in the PMF are poorly determined. In contrast, path-restrained methods by nature enforce sampling at all parts of the path including high free-energy regions. It is also possible that a major factor leading to this limited sampling of the free-energy barrier in ABPO is the choice of reduced variables to capture the SrcCD transition. As a directed approach, ABPO provided here in a reasonable amount of simulation time (1–10 µs) a straightforward view of the structural features of the transition process. The resulting trajectories readily afford an atomistic description of the transition process from a combined assessment of the free energy along the path and corresponding analysis of conformational properties along the path, highlighted in certain cases by the RV profiles.

By utilizing this combined assessment, the work presented here yielded new insight into the conformational inactivation/activation of Src CD. First, large-scale correlated motions near the FE maximum are apparent from the RV profiles (Fig. 2). The internal distances composing RV3, RV5, and RV11 capture concerted motions for rotation of the αC helix, rearrangement in the mid-region of the A-loop, and motion of the A-loop relative to the C-lobe. Furthermore, the path profiles of the inter-residue distances (Fig. 6) demonstrate the important role of the SEN exchange partners in this concerted motion. Thus, the concerted motion involves the E310 switch from a close interaction with K295 in the active state to interaction with R409 in the inactive state (Fig. 6), with the concomitant switch of R409 away from being engaged with Y416 in the active state. Second, the A-loop motion is complex and occurs over the length of the path with structural changes on both sides of the FE maximum, in contrast to the rotation of the αC helix, which occurs over a short segment of the path at the free-energy barrier (Fig. 7). For inactivation, the extended N-terminus of the A-loop first moves inward of the αC helix, allowing outward rotation of the helix, followed by folding in of the A-loop and formation of the single-turn H2 helix over the catalytic site. This description, we find, is consistent with the sequence of events put forward in other studies.^{9,10,17,31,38,46} Together, we learn that the SEN contributes to the mechanism of the coupled, interdependent motions of the A-loop and αC helix in the transition process.

IV. METHODS

A. Simulation systems

Src kinase domain in active and inactive states are from the PDB entries 1Y57³⁵ and 2SRC,³⁶ respectively. Residues 255–521 were included in the simulations. All ions, ligand, and crystal waters were removed from the structures. The coordinates of the missing atoms in the two structures and all hydrogen atoms were added using the CHARMM IC BUILD facility. Simulations of the proteins were carried out using the CHARMM 22 all-atom force field with CMAP dihedral angle corrections with the implicit solvent model FACTS. To prepare the systems for ABPO, we first performed energy minimization on the two crystal structures. The energy was minimized using the steepest descent and Powell algorithms to a gradient less than 1.0. The initial velocities were generated from Gaussian distributions at 100 K, and then, the energy-minimized structures were heated to and equilibrated at 298 K for a total of 500 ps. The leapfrog integrator was used to calculate the trajectories with a 2 fs time step.

A 10-ns simulation in Langevin dynamics was initiated using coordinates from the end of the equilibration run at 298 K. The long-range interactions cutoff distances were set to 10 Å, 12 Å, and 14 Å. The time series of temperature, potential energy, and root-mean-square deviation (RMSD) of heavy-atom coordinates with respect to the energy-minimized structure were monitored to assess the stability of the simulation. The closest-to-average structures from the last 4 ns of the trajectories were used to define the distance RVs to set values for the RVs at the end-states and initiate the ABPO simulations.

B. ABPO parameters and transition path computation

The transition pathway was optimized using the ABPO module implemented in CHARMM. The theoretical foundation of ABPO has been described,¹⁰ and its implementation is previously described in detail.^10,18 For an abbreviated description, ABPO proceeds in cycles, and for the ith cycle,

• i.Evolve replicate trajectories for a block of N steps with the potential V = V_MM + V_T + V_b, where V_MM is the molecular mechanics function, V_b is the bias potential [Eq. (1)], and V_T is a one-sided harmonic tube-wall potential to limit sampling to configurations within a tube-shaped space of the current path. V_T is zero within the tube radial distance from the path.
• ii.Determine from the aggregate histograms accumulated over replicate trajectories visits to path slices (hyperplanes).
• iii.If insufficient visits at all slices, increment the block number by 1 and go to i. If sufficient visits, update the path to the mean positions and apply a smoothing and spacing routine for the slice points to obtain the ith path.
• iv.Check the distance between the ith and (ith-1) path. If greater than a threshold, set the block number to 1 and go to i. If less than a threshold, stop.

The parameters specific to the Src transition pathway are summarized here. The path was initially defined starting with the active and down-regulated end-state structures obtained from equilibrium MD described above in Sec. IV A. Eight replicate trajectories were launched from each end-state, thus averaging over 16 total replicas for sampling the transition path. The initial path was set to be the linear value of the RVs between each end-state. The path was evolved in cycles comprising multiple blocks set to 40 000 time steps. At the end of each block, the extent of path sampled was assessed, and if the path was sampled sufficiently over the full path length, the cycle was terminated and the path coordinates were updated to start the next cycle. The maximum number of blocks per cycle was set to 30 so that the cycle was terminated with a maximum 2.4 ns per replica, and the path coordinates updated for the next cycle. In all simulations, Langevin dynamics was used at 298 K with a time step of 2 fs. The fraction of the free energy canceled by the bias potential was 0.8 [b in Eq. (1), CHARMM BFCT = 0.8]. The coupling of the bias to the dynamics was 2.5 t⁻¹ [c in Eq. (1)]. The histogram for visits to path slices is smoothed using a Gaussian mollification factor set to 0.05. The number of slices was set to 2000 as indicated in the plots for each path to achieve the desired sampling resolution along the path. For the tube radius and potential parameters, the radius was 20 Å, and the force constant was 5 kcal/mol to enable efficient sampling of the system. The tube radius was chosen based on an estimation of the RMSD difference between the two states.

The metric tensor D was evaluated using Eq. (2) in Ref. 10. D was evaluated from short unbiased simulations at each end-state, and the inverse of D was stored for input to ABPO. For the Src kinase domain, D was estimated from 2 ns unbiased simulations with a 2 fs time step. The D is viewed as a constant for further calculations.

RV plots (Fig. 2) were used to follow the evolution and convergence of the ABPO path in the reduced-variable space. Each RV path-profile is updated at the end of an ABPO cycle and monitored for converging to a stable profile over consecutive cycles. Reasonable convergence was achieved with 100 cycles and a total simulation time of 1.446 µs. Adaptive sampling of the optimized path after 100 ABPO cycles was 384 ns for computing the PMF and structural analysis of the path.

C. Reduced variables of the ABPO inactivation path for Src CD

The ABPO calculation is conducted in a reduced variable (RV) space to adaptively bias sampling on a path that defines the transition progress between the two known end-states. The conformational transition was characterized in terms of four regions of the Src CD: αC helix, N-lobe excluding the αC helix, A-loop, and C-lobe excluding the A-loop. The residue numbers for each region are listed in Table S3. Following the previous work,¹⁷ RVs were defined to capture the relative position of two protein regions having large structural differences between the active and inactive forms. Inter-residue distances were specified between the region pairs αC helix–N-linker, αC helix–N-lobe, αC helix–A-loop, αC helix–C-lobe, A-loop–A-loop, A-loop–N-lobe, and A-loop–C-lobe. The Cα–Cα distances ≥2.5 Å were extracted from the closest-to-average active and inactive structures from the 10 ns equilibrium simulations. For the residues with long side chains, movement of the sidechain was captured by including the farthest heavy atom from the Cα atom for some RVs in the inter-residue distances of Cα–sidechain and sidechain–sidechain. The sidechain-related pairs were included for cases where the difference in the Cα–Cα distance between the two states is smaller than the sidechain–sidechain distance difference.

Residue pairs were combined to form an RV Z according to

$$Z={\sum }_{j=1}^n\frac{r_j^{state1}-r_j^{state2}}{|r_j^{state1}-r_j^{state2}|}{r}_j,$$ (3)

where n is the number of residue pairs, r_j is the inter-atom distance of residue pair j, and $r_j^{statex}$ is the value of the residue pair in the state x. Preliminary ABPO simulations for ∼10 cycles were used to refine the definition of the RVs and eliminate inappropriate reduced variables. Inappropriate RVs were determined using the criteria: (1) a lack of the system sampling long portions of the path and the maximum number of blocks was reached in each cycle, (2) the normalized RV does not evolve from 0 to 1 at the path ends (not applied to RVs with residues in the flexible N-linker), and (3) the normalized RV profiles are not reproducible among independent simulations with identical input. The RV profiles that are not reproduced well are thought to indicate flexibility as the basis for differences among the two states and that the conformational difference may not be energetically important to the transition. A complete list of the final RVs is in Table S2.

D. Data analysis

The normalized RVs are calculated using the following equation:.

$$\text{R}{\text{V}}_{\text{normalized}}=\frac{\left(\text{R}{\text{V}}_{\text{i}}-\text{R}{\text{V}}_{\text{state}1}\right)}{\left(\text{R}{\text{V}}_{\text{state}2}-\text{R}{\text{V}}_{\text{state}1}\right)}.$$ (4)

For each RV, RV_state1 and RV_state2 are the RV values for the two end-states, respectively, while RV_i is the value on the ith slice.

The PMF profile is smoothed as described. Taking the raw PMF data array as x, a window length of window_len = 160 is used for data processing. The subarray of window_len from each end of the PMF profile is padded before slice 0 and after slice 2000 as preprocessing to generate data array s. Then, numpy window function hanning is used to generate a window array w with the length of window_len. The smoothed array y is generated by calling numpy.convolve[w/w.sum(), s, mode = “valid”]. The final plot shows slice 0–2000 of data array y.

SUPPLEMENTARY MATERIAL

See the supplementary material for explanation and figures from MD simulations for the two stable end-states of activated and downregulated Src CD for the mainchain dihedral angle distributions (Fig. S1) and N linker structures (Fig. S2) and Table S1 listing residue numbering for regions of the domain structures, Table S2 providing details of the 11 RVs and listing the inter-residue distances for each, and Table S3 listing residue numberings of structural features of the CD domain.

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.