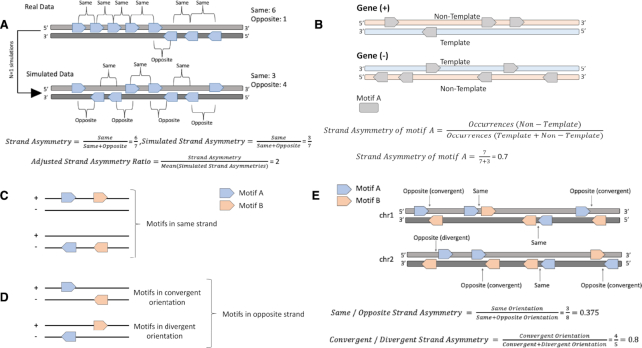
Figure 2.
Schematic of strand asymmetry analyses across different scenarios. (A) Estimation of biases in the orientation patterns of consecutive occurrences of a motif relative to those found in the shuffled simulated data. Calculation of orientation patterns for consecutive motif occurrences is performed using the function consecutive_patterns.py function. In the presented example, there are seven motifs, six of them in the same orientation and one in the opposite orientation. We perform N simulations (in the schematic N = 1) and calculate the adjusted strand asymmetry ratio and empirical P-value. In this simple case, simulated strand asymmetry = 3/7 < strand asymmetry = 6/7, so the set of successes, as defined in the methods section, for which the simulated asymmetry is higher than the strand asymmetry has a cardinality of 0. This results in a trivial P-value of 1, as is to be expected from only a single simulation. (B) Estimation of transcriptional strand asymmetry of a motif in genic regions. Genes in both orientations are shown. Calculation of transcriptional strand asymmetries can be performed using the function contained_asymmetries.py. In the schematic, there are ten motifs distributed across two opposite oriented genes; the null hypothesis is that they are equally-likely to have either orientation relative to the gene direction. There are seven motifs in the non-template orientation resulting in 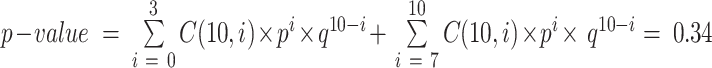 , calculated with the two-tailed binomial test. Motifs can occur in (C) same (++ and –) or (D) in opposite (+- and −+) strand orientations. The order of two same-type or different motifs is not taken into consideration because the double strand DNA molecule is bidirectional; nevertheless, if a third strand-oriented feature was included, their order would be another factor to account for. (D) For those motifs in opposite strands, they can be separated in convergent (+−) or divergent (-+) orientations. These orientations of motif pairs are specific to non-palindromic motifs. (E) Orientation of motif pairs and estimation of same/opposite and convergent / divergent strand asymmetry ratios using a miniature genome example of two chromosomes and several occurrences of two motifs in pairs. Calculation of the strand asymmetry for motif pairs is performed with the function pairwise_asymmetries.py. In the schematic, there are eight motif pairs, across the two chromosomes; the null hypothesis is that they are equally-likely to have same or opposite orientation and in the subset of opposite orientation cases, they are equally likely to be in convergent or divergent orientation. There are three motif pairs in same orientation, resulting in
, calculated with the two-tailed binomial test. Motifs can occur in (C) same (++ and –) or (D) in opposite (+- and −+) strand orientations. The order of two same-type or different motifs is not taken into consideration because the double strand DNA molecule is bidirectional; nevertheless, if a third strand-oriented feature was included, their order would be another factor to account for. (D) For those motifs in opposite strands, they can be separated in convergent (+−) or divergent (-+) orientations. These orientations of motif pairs are specific to non-palindromic motifs. (E) Orientation of motif pairs and estimation of same/opposite and convergent / divergent strand asymmetry ratios using a miniature genome example of two chromosomes and several occurrences of two motifs in pairs. Calculation of the strand asymmetry for motif pairs is performed with the function pairwise_asymmetries.py. In the schematic, there are eight motif pairs, across the two chromosomes; the null hypothesis is that they are equally-likely to have same or opposite orientation and in the subset of opposite orientation cases, they are equally likely to be in convergent or divergent orientation. There are three motif pairs in same orientation, resulting in 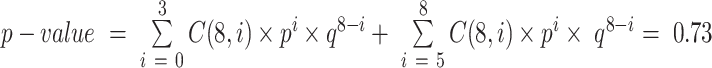 and there are five motif pairs in opposite orientation resulting in
and there are five motif pairs in opposite orientation resulting in 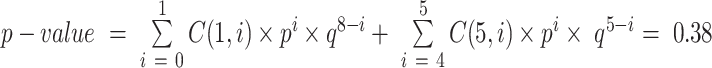 , for same/opposite and convergent/divergent strand asymmetries, respectively, calculated with the two-tailed binomial test.
, for same/opposite and convergent/divergent strand asymmetries, respectively, calculated with the two-tailed binomial test.