Abstract
Multilevel thresholding image segmentation has received considerable attention in several image processing applications. However, the process of determining the optimal threshold values (as the preprocessing step) is time-consuming when traditional methods are used. Although these limitations can be addressed by applying metaheuristic methods, such approaches may be idle with a local solution. This study proposed an alternative multilevel thresholding image segmentation method called VPLWOA, which is an improved version of the volleyball premier league (VPL) algorithm using the whale optimization algorithm (WOA). In VPLWOA, the WOA is used as a local search system to improve the learning phase of the VPL algorithm. A set of experimental series is performed using two different image datasets to assess the performance of the VPLWOA in determining the values that may be optimal threshold, and the performance of this algorithm is compared with other approaches. Experimental results show that the proposed VPLWOA outperforms the other approaches in terms of several performance measures, such as signal-to-noise ratio and structural similarity index.
Keywords: Image segmentation, Multilevel thresholding, Swarm algorithm, Volleyball premier league algorithm, Whale optimization algorithm
Introduction
The segmentation is a fundamental and crucial step in image processing and artificial vision. A significant number of applications explored the process of segmentation, such as medical imaging [29], video semantic [38], script identification [26], historical documents [51], and remote sensing [47]. Segmentation is defined as an operation that partitions the image into several homogeneous objects. Mainly, the segmentation image includes several techniques such as thresholding, edge detection, split and merge method, and region growing [47].
Among the methods mentioned above, thresholding is the most used and exploited due to its efficiency and more straightforward implementation. Typically, two variants of thresholding are widely used in the literature known as binary thresholding (bi-level) and multilevel thresholding (ML-TH). The main idea of binary thresholding is to find the optimal value of threshold (T), which aims to create two classes by comparing the pixel intensity to T. The lower values are affected to the first class while the higher values are assigned to the second class.
Generally, ML-TH is the most exploited in image processing because the number of classes is more significant than the two classes. Besides, this type requires several values of thresholds. The main problem of thresholding is how to find automatically the optimal value of threshold(s), which leads to determining the number of clusters (classes) correctly.
For binary thresholding, we distinguish two strategies. The first one is introduced by Otsu in [36] that aimed to maximize the variance between classes. The second strategy is provided by Kapur [24] that used the entropy criteria as a measure to maximize the homogeneity between classes.
For ML-TH, a new class of metaheuristic algorithms based on genetic evolution, swarm theory, and physical laws have been applied. Several methods, such as genetic algorithm (GA) [45], differential evolution (DE) [41], particle swarm optimization (PSO) [2], multi-verse optimizer (MVO) [11], artificial bee colony (ABC) [14], artificial bee colony (ABC) [18], chicken swarm optimization [28], electromagnetism optimization [34], and gravitational search algorithm (GSA) [31], are available in the literature. They are applied to obtain the optimal set of thresholding by maximizing the interclass variance defined by Otsu’s function.
Recently, the intention of scientific is attracted by the simulation of the natural behavior of insects and animals, which increase the development of several algorithms. We find the work of Farshi in [16] that introduced a novel technique named animal migration optimize for finding the optimal set of multiple thresholds. The author used two criteria most exploited in the field of image thresholding known as Kapur entropy and Otsu method. The experimental study showed better results in comparison with other optimization algorithms such as GA, PSO, and BFO. In [7], the authors proposed three heuristics based ML- thresholding, namely OA-TH, PSO-TH, and GWO-TH, for selecting the optimal thresholds. The authors used the Otsu method to maximize the between-class variance. The experimental results demonstrated the high performance of WOA-TH compared to GWO-TH and PSO-TH.
In the same context, in Ref [22], the authors proposed a novel enhanced version of bee algorithms (BAs) to multilevel image thresholding, called PLBA. This algorithm aimed to determine the optimal values of the threshold by maximizing between class-variance and Kapur’s entropy. Besides, this algorithm included two searches (i.e., local and global). The first one applied the greedy Levy local algorithm [39], which is based on the levy flight operator. Also, the global search incorporated the path levy in the initialization phase that is used in PLBA. The PLBA outperformed other metaheuristic algorithms.
A new approach to multilevel thresholding based on GWO is developed by [25]. The researchers imitated the social life of wolves, which usually depended on their leadership hierarchy and hunting activities. The proposed method selected the optimal threshold values using the criteria of Kapur’s entropy or Otsu’s between-class variance. The experimental results showed that the GWO provided an excellent performance over BFO and PSO. Moreover, the computational complexity of GWO is greatly diminished because it was faster than the BFO.
Mohamed et al. [9] proposed two algorithms based on swarm intelligence, called whale optimization algorithm (WOA) and moth-flame optimization (MFO), for multilevel threshold segmentation. The WOA emulated the natural cooperative behavior of whales, whereas the MFO mimicked the behavior of moths, which have a unique navigation style at night based on the moonlight. Otsu’s between-class variance evaluates the fitness function, and the experimental result showed that MFO provided a better result than WOA.
The authors of [4] developed a novel multilevel thresholding algorithm based on swarm intelligence theory, called krill herd optimization (KHO), which simulates the herding behavior of krill agents. This study introduced the KHO to find the optimal threshold values of image segmentation by maximizing the Kapur and Otsu measures. A comparative study showed that the proposed method outperformed other existing bio-inspired approaches, such as GA, MFO, and PSO.
The segmentation of color images has recently grown remarkably in image processing. A new method has been proposed [20], which presented an improved version of the FA, called MFA, by minimizing cross-entropy, intra-class variance, and Kapur’s method. The main difference between MFA and FA resided in the initialization and movement phase. The initialization phase is conducted by a chaotic map, which improved the diversification and convergence, whereas the phase of the movement is based on PSO.
Physical and mathematical theories attracted the attention of researchers, which allows to develop several algorithms for MLT. This category included sine cosine algorithm (SCA) [19], Multiverse optimizer (MVO) [23], Electro-magnetism (EM) [6], Equilibrium Optimizer (EO) [48] and Gravitational Search Algorithm [44].
Physical rules are considered as a new source for studying the ML-TH, for example Xing and Jia [49] proposed a multi-threshold image segmentation based on grey level co-occurrence matrix (GLCM) and improved Thermal exchange optimize (TEO) using two operators: levy flight and oppsition-based-learning (OBL). To validate the efficiency of the proposed method, natural-color image, satellite image, and Berkeley images are taken as an experiment. GLCM-ITEO has shown a high quality of segmentation with less CPU time.
An improved thermal exchange optimization using a levy flight function is proposed [50]. For validating the efficiency of LTEO, six swarms are used for comparison tested on color nature image and satellite image. The experimental study has shown high accuracy of segmentation and speed convergence.
Recently, the use of the volleyball premier league (VPL) algorithm proposed by Moghdani et al. [32] is a known great success for solving global optimization problems. In general, the VPL consists of applying several strategies inspired by a volleyball game, which are used to improve the population during the seasons. The VPL showed some difficulties in terms of convergence and local optima. So, the learning phase has the most substantial effect on the performance of the VPL algorithm. To avoid the problem of convergence and to enhance the learning phase, we integrate the whale optimization algorithm (WOA), which is used as a local search.
In general, the WOA emulated the behavior of whales during the searching for prey [30]. The WOA has been applied to different applications based on these characteristics (e.g., economic dispatch problem [46], bioinformatics [3], feature selection [42], and content-based image retrieval [10]).
The main contributions of this paper are:
For the first time, the sports inspiration based on basic VPL is applied for multilevel thresholding
A new hybrid algorithm called VPLWOA is developed for selecting the optimal threshold values on various images by maximizing the between class-variance defined by Otsu’s function.
Assess the quality of the proposed VPLWOA using eleven natural images that have different properties.
A new real application of blood cell segmentation based on VPLWOA is realized to find the optimal thresholds.
Experimental results show that VPLWOA outperforms other different metaheuristic algorithms in terms of performance criteria.
The general structure of the paper takes the form of five chapters. Image segmentation using Otsu’s function, the VPL algorithm, and the WOA are described in Section 2. The proposed method (i.e., VPLWOA) is explained in Section 3. A comprehensive evaluation of our method with a statistical study of various images is presented in Section 4. Finally, our conclusion and future work are discoursed in Section 5.
Related work
Recently, many studies are explored by the researcher for understanding the behavior of the life cycle of insects, animals, and nature or physical theory. These inspirations lead deeply to appear several thresholding algorithms inspired from genetic as evolutionary algorithms. More recently, the swarm intelligence family still more attractive with the simulation of insects and animal’s life including harris hawks, ant lion, whales grey wolves, salps, ant’s colonies, bees. In this side, several algorithms are introduced for multilevel thresholding images including Harris hawk’s optimizer, grey wolf optimizer, ant colony optimization, artificial bee colony ant lion optimizer, whale optimization algorithm, salp swarm algorithm.
Recently, Eric et al. [40] introduced an efficient swarm optimizer called harris hawks optimizer (HHO) for solving multilevel thresholding based on minimum cross-entropy. The authors treat the standard benchmark of images and medical mammograms. The proposed method is shown their efficiency compared to basic machine learning and metaheuristics approaches, including PSO, FFA, DE, HS, SCA, and ABC in terms of PSNR, FSIM, SSIM, PRI, and VOL. In addition, HHO consumed less time compared to PSO, FFA, and DE.
In this literature review, we give more importance to segmentation images based on hybrid metaheuristics. For example, Abdelaziz et al. [12] developed a new hybrid algorithm based on the HHO and salp swarm algorithm (SSA) for finding the optimal values of the multilevel threshold. The general idea consists of dividing the population into two parts, where the process of exploration and exploitation of HHO is applied to the first part, and the searching process of SSA is used for updating the solutions of the second part. The proposed method HHOSSA achieved high performance compared to original versions of HHO and SSA in terms of PSNR and SSIM, tested on natural gray-level images.
Ahmadi et al. [1] proposed a hybrid algorithm for seeking the optimal values of the level threshold using differential evolution (DE) and bird mating optimization (BMA). The numerical results have shown the high performance of the proposed method assessed on standard test images and compared to other optimizers like PSO, PSO-DE, GA, Bacterial foraging (BF), and enhanced BF in terms of fitness and standard deviation.
In the same context of MLT segmentation image based on hybrid metaheuristics, a new combination between Spherical search optimizer (SSO) and sine cosine algorithm (SCA) is developed by Husein et al. [33]. The fuzzy entropy is considered as the main fitness function for testing the quality of the segmented image. The experimental study is assessed on several images taken from Berkeley datasets and the obtained results of SSOSCA outperformed other optimizer that included Cuckoo search (CS), Grey wolf optimizer (GWO), WOA, SCA, SSA, SSO, GOA over different performance metrics as PSNR, FSIM, and SSIM. The proposed method took a lower time for achieving the segmentation task compared to other optimizers.
In [5], The authors introduced a new hybrid algorithm called HHO-DE for MLT color segmentation image. Their idea consists of dividing [5] firstly the main population into two equal subpopulations. Secondly, HHO and DE update the position of each subpopulation in a parallel way. Two fitness functions are used based on Otsu and Kapur entropy to determine the optimal set of threshold levels. The experimental results indicated that HHO-DE could be considered as an efficient tool for MLT color image segmentation compared to other optimizers as DE HHO SCA BA HSO PSO DA according to PSNR SSIM and FSIM measures.
With the fast propagation of COVID-19, several researchers presented many solutions for the detection and segmentation of chest CT gray-level images. In [13], the authors proposed a new version of the marine predator’s algorithm (MPA) improved by MFO based on fuzzy entropy. The proposed method MPAMFO presented their efficiency compared to the existing swarm intelligence works in terms of PSNR and SSIM.
Sun et al. [43] introduced an algorithm called GSA-GA, which combined GSA with a genetic technique for multilevel thresholding. This algorithm used the roulette selection and mutation operator inspired by genetic technique, which is integrated into GSA. Two standard criteria (i.e., entropy and between-class variance) are used as fitness functions. The statistical significance test demonstrated that GSA-GA considerably diminished the computational complexity of all images tested.
Furthermore, Oliva et al. [35] proposed a new evolutionary algorithm that combines Antlion optimization and a sine-cosine algorithm to determine the optimal set of thresholding segmentation using Otsu’s between-class variance and Kapur’s entropy. According to the experimental study, the SCA does not outperform other evolutionary computation from state of the art.
Ouadfel and Taleb-Ahmed [37] investigated the ability of two nature-inspired metaheuristics, called social spiders optimization (SSO) and flower pollination (FP) to solve the image segmentation via multilevel thresholding. During the optimization process, each solution is evaluated using the between-class variance or Kapur’s entropy. The experimental results illustrated that the SSO and FP better than PSO and bat algorithms. Furthermore, the SSO guaranteed a balance between exploration and exploitation and showed the stability of results for all images.
Background
In this section, the necessary information of the multilevel thresholding image segmentation using Otsu’s function, VPL, and WOA are discussed.
Problem formulation
In this section, the definition of the multilevel thresholding problem is explained. Assumed that the tested image I contains a set of K + 1 classes, and a set of K threshold values (tk, k = 1, 2…, K) are required to divide I into these classes (Ck, k = 1, 2…, K). This condition can be represented by the following equation [37]:
| 1 |
where L is the gray level of I.
In general, the task of determining the optimal threshold values to segment the image is by conversion to an optimization problem through maximizing or minimizing a specific objective function. We suppose the maximization in this paper, which is defined as follows:
| 2 |
Where F is the objective function used to evaluate each solution. In the following sections, the most popular two functions used in the multilevel threshold image segmentation are defined.
Otsu’s method
In [36], the description of the Otsu’s method was given. This method aims to maximize the variance between the classes of the given image I using the following equation:
| 3 |
| 4 |
where μ1 is the mean intensity of the image I; and Pi and Fri are the probability and frequency of the ith gray level of the image, respectively. The total number of pixels in the image is given by Np.
Volleyball premier league algorithm
This subsection is demonstrated the mathematical modeling of the proposed algorithm, Volleyball Premier League algorithm (VPL) [32], which is explained comprehensively. The general flow of VPL is presented in Fig. 1, including all steps of the proposed algorithm.
Fig. 1.

The framework of the VPL algorithm
In this algorithm, we use two parts that contain formation and substitutes for each solution, wherein random numbers are used in the identified interval values, as shown in Eqs. (5) moreover, (6) [32]:
| 5 |
| 6 |
where lbj and ubj denote the range of variable j, respectively; and Rand() is a random number generated between zero and one. In the VPL algorithm, we perform a well-known procedure, which is named single round robin (SRR), to provide the league’s schedule.
In the typical volleyball game, the better team can beat its rival in the match. Each team has a chance of running up against its competitors according to the probability rules in the match. The power index π(i) is defined on the basis of the following formulas:
| 7 |
| 8 |
In the above formulas, denotes the objective function of the ith team, which is calculated based on its formation property; Z denotes the summation of the objective function in the current iteration. Moreover, the following formulations are given to compute the π value for both teams, which are going to play each other in this match.
| 9 |
| 10 |
where and denote the position of formation property of teams j and k, respectively. Therefore, we can compute the probability of winning team j against k with the following formula:
| 11 |
According to the laws of probability, the following formula is given as:
| 12 |
A new formation and corresponding strategies are used for the winner and loser teams, considering that the winning team is determined. In this regard, different operators, including knowledge sharing, repositioning, and substitution, are used for the loser team, and the winning team operates the leading role strategy. Generally, the coach shares his knowledge about the condition of the game with players to obtain improved performance. Thus, knowledge sharing strategy can be specified by:
| 13 |
| 14 |
In the above formulas, we have defined coefficients values (λf andλs) for formation and substitutes properties; and also, two new random numbers, which are indicated r1 and r2, are uniformly engendered in range zero to one. Furthermore, the rate of sharing knowledge is indicated by δks which is computed as follows:
| 15 |
where Nks denotes the amount of knowledge sharing for any solution, and J is considered as the amount of positions in solutions. Repositioning is a common strategy, which has considerable effects on a volleyball game during a match. This operator positions the best players in the ideal to attain excellent performance. On this basis, we mention δrs as the rate of repositioning procedure, and the number of this operator in the current iteration is given as:
| 16 |
where Nks states the number of this operator in each iteration. At this point, we randomly select two positions (i.e., i and j), and α and β (two virtual objects) are used for storing the value of active and passive players, respectively. Then, the properties of solutions i and j to are assigned to α and β. Therefore, the following formulas are given:
| 17 |
| 18 |
| 19 |
| 20 |
At the end of this process, the following formulas are given, which are indicated that properties of selected positions (A and B) are assigned to each other reversely.
| 21 |
| 22 |
| 23 |
| 24 |
We can increase our knowledge in performing the corresponding operators in this algorithm by understanding the similarities and differences among sports. Therefore, the coaches use substitution for the intervention to find the best formation for their teams. The number of substitution (Ns) in each iteration is calculated by the following formula::
| 25 |
Where r represents a random number that is distributed uniformly between zero and one, and J specifies the dimension of each solution, which is identified as the number of players in this algorithm. As previously mentioned, some operators are used just for the loser team and substitution strategy. On this basis, let set h, F, and S denote randomly selected position indexes, formation, and substitution property of the loser team, respectively. Subsequently, these property values of all players of set h are swapped together. The specific operator, named the winner strategy, is given, which is similar to those used in many evolutionary methods, such as PSO, to reach this goal in the proposed algorithm [8]. In this operator, first, we determine the position of the winning team and combine it with a random one to obtain a new position using the following formulas:
| 26 |
| 27 |
Where ψf and ψs symbolize inertia weights of formation and substitute properties, respectively, and r1 and r2 are random numbers, which are generated uniformly in [0, 1]. In the learning operator, coaches examine the behavior of teams for obtaining the best results to enhance their teams’ performance. Moreover, we define the formula to explain the learning phase as follows:
| 28 |
where g signifies a set that compromise substitute and formation properties (g = {s, f}), and index Φ yields a value from one to three, which indicates the first, second, and third best solutions, also known as ranks 1, 2, and 3, respectively. shows the value of position j of property g with respect to the best solution Φ. is the value of position j of the current iteration t. Finally, θ and ϑ are coefficient values, which are defined as follows:
| 29 |
| 30 |
Where r1 and r2 are random numbers that are uniformly generated between zero to one, and b is linearly decreased from β to zero, which is computed as follows:
| 31 |
The coaches pursue to recognize the best combination of active (formation) and passive players (substitutes) concerning the top three teams in the league. Therefore, the following formulas are assumed to capture the learning phase for formation property:
| 32 |
| 33 |
| 34 |
| 35 |
Similarly, the formulas mentioned above can also be used for substitute property by using term s instead of f in the corresponding position. Notably, we have used these formulas to enhance the exploitation process of the proposed algorithm. The transfer process takes place when a season ends. On this occasion, the players can move among teams. On this basis, we have mathematically expressed this concept in the proposed algorithm to perform the convergence toward an optimal solution.
Let set H be the randomly selected teams for this operator if only if a random value (r), generated randomly between 0 to 1, is greater than 0.5. Thus, the number of teams involved in the season transfer is expressed as follows:
| 36 |
where δst denotes the percentage of teams in this operator. Similar to the typical league in a volleyball game, top teams of any league go up to a higher division. Consequently, the worst teams are dropped down to the lower division. While only one league exists in this algorithm. The relegation of the worst teams is considered in this operator, which is called promotion and relegation. Thus, we intentionally eradicate the worst teams and then exchange them by new ones that are generated randomly. Let Npr be the number of teams moving up to the upper league, and N be the total number of teams in the current league.
| 37 |
where δpr symbolizes the percentage of teams, which are relegated and promoted accordingly.
Whale optimization algorithm
The WOA is presented in [30] as a new metaheuristic algorithm based on the social behavior of the humpback whales.
Moreover, the WOA begins by randomly generating a set of N solutions TH, which represents the solution for the given problem. Then, for each solution THi, i = 1, 2, …, N, the objective function is computed, and the best solution is determined TH∗. Subsequently, each solution is updated either by using the encircling or bubble-net methods. In the bubble-net method, the current solution THi is updated using the shrinking encircling method, in which the value of a is decreased, as shown in the following equation:
| 38 |
where g and gmax are the current iteration and the maximum number of iterations, respectively.
Also, the solution THi can be updated using the encircling method, as shown in the following equation:
| 39 |
| 40 |
where D is the distance between TH∗ and THi at the gth iteration. The r1and r2 represent the random numbers, and the symbol ⨀ is the element-wise multiplication operation. Moreover, the value of a is decreased in the interval [2, 0] with increasing iterations using Eq. (38).
Also, the solution THi can be updated using the spiral method that simulates the helix-shaped movement around the TH∗, as shown in the following equation:
| 41 |
where l ∈ [−1, 1] and b are the random variables and constant value used to determine the shape of a logarithmic spiral.
Moreover, the solutions in the WOA can be updated by using either the spiral-shaped path and shrinking, as defined in the following equation:
| 42 |
where r3 ∈ [0, 1] represents the probability of switching between the spiral-shaped path and shrinking methods.
The whales can also search on the TH∗ by using a random solution THr, as follows:
| 43 |
According to [30], the process of updating the solutions depends on a, A, C, and r3. The current solution THi is updated using Eq. (41) when r3 ≥ 0.5; otherwise, it is updated using Eqs. (39)–(40) when |A| < 1 or Eq. (44) when |A| ≥ 1. The process of updating the solutions is repeated until the stopping criteria are satisfied.
Proposed method
In this section, the main steps of the proposed VPLWOA for determining the optimal threshold values for image segmentation are discussed. The VPLWOA depends on improving the VPL algorithm using the operators of the WOA. Hence, the method is called VPLWOA. In the VPLWOA, the Otsu’s function (as defined in Eq. (3)) is used to evaluate the quality of each solution.
The proposed approach begins by computing the histogram of the given image I, and then generates a random set of N teams (TH) as:
| 44 |
| 45 |
where LHj and HHj are the lower and higher histogram values at the jth dimension. The next step in the proposed VPLWOA approach is to create the league schedule and evaluate the quality of each team THi by computing the objective function (as defined in Eq. (2)). Then, the VPLWOA performs the competition between each team to determine the loser and winner teams using Eqs. (9)–(10). Knowledge sharing, repositioning, and substitution strategies are used to improve the behavior of the loser teams; whereas, the leading role strategy is applied for the winning teams. Thereafter, the behaviors of all competitive teams are enhanced during the modified learning phase (the main contribution). The VPLWOA can simultaneously update the behavior of the team by using the operators of the WOA and traditional learning phase, as shown in the following equation:
| 46 |
where r5 ∈ [0, 1] is a random number used to switching between the VPL and WOA. The Probi represents the probability of the fitness function (fi) for the ith team and is defined as follows:
| 47 |
The next step in the proposed VPLWOA is to use the promotion and relegation and season transfer processes similar to the traditional VPL. The previously mentioned steps are performed until the terminal criteria are satisfied. The full steps of the developed VLPWOA are given in Algorithm 1.
Experiments and discussion
In this section, a set of experimental series is performed to verify the performance of the proposed VPLWOA method. Two different sets of images are also used, and the results of VPLWOA are compared with other methods. The parameter setting and performance measure to evaluate the performance of the algorithms are discussed in this section. Then, experimental series one is performed using the first set of images that contains eleven images. Experimental series two is performed using the second set of images that have six medical graphics for leukemia blood cells.
Parameter setting
The results of the proposed VPLWOA are compared with the other five methods. These methods are social-spider optimization [37], sine–cosine algorithm [35], FA [21], WOA [9], and traditional VPL [32]. These approaches are selected because their performance is established in several fields, including image segmentation. However, the VPL is used for the first time in image segmentation.
The value of the parameters for each algorithm is set similar to the original reference. The size of the population and the maximum number of iterations are set at 25 and 100, respectively. Each algorithm was executed 25 independent times along with each threshold level overall the tested images. A total of eight different levels of the threshold are used to segment each image to two, four, six, eight, 10, 16, 18, and 20. All the algorithms are implemented using MATLAB 2017b, which is installed in Windows 10 (64 bits).
Performance measures
A set of three performance measures are used to verify the performance of proposed VPLWOA, including peak signal-to-noise ratio (PSNR) Eq.(48), structural similarity index (SSIM) Eq. (50), fitness value (Otsu’s method is used as a fitness function), and CPU time. All results are tabulated and summarized in figures.
| 48 |
| 49 |
| 50 |
where I and Is are the original and segmented images, respectively; μI and are the mean intensities; and determine the standard deviation; σ is the covariance; c1 = 6.502; and c2 = 58.522.
Experimental series 1: benchmark images
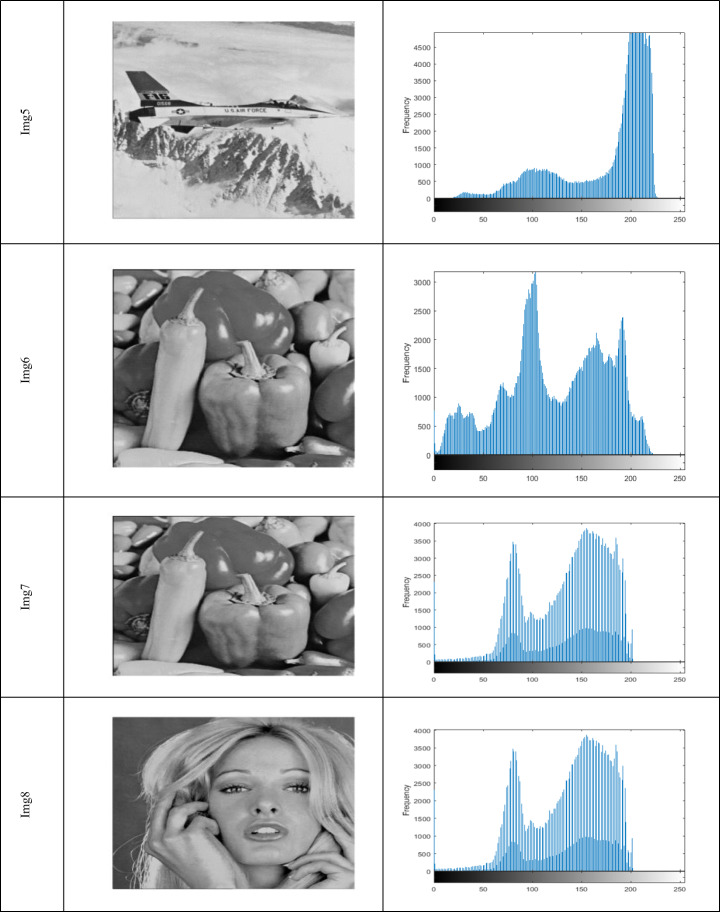
In this experimental series, a set of eleven benchmark images are used to evaluate the accuracy of the VPLWOA to determine the optimal threshold values. These images have different properties, such as variant size, and resolutions. The histogram for the tested images is given in Fig. 2.
Fig. 2.
Original images and their histogram
The comparison results of the VPLWOA with the other five methods are given in Figs. 5, 6, 7, 8 and 9 and Table 2 and For further analysis, the CPU time results for each algorithm are recorded in Table 3. From this table, the VPLWOA achieved the best results in 21 cases and is ranked third after both WOA (with 27 cases) and SSO (with 24 cases). The SCA obtained the fourth rank (with 10 cases) followed by the FA (with 6 cases), it was ranked fifth. Whereas, the VPL was considered as the slowest algorithm in the experiments. The VPLWOA showed good CPU time in a large threshold than the smallest one.
Fig. 5.
Average of the PSNR for all algorithms at each threshold level
Fig. 6.
a SSIM ranking of all algorithms. b Ranking of the fitness values
Fig. 7.
Average of the SSIM for all algorithms at each threshold level
Fig. 8.
Average of the fitness values for all algorithms at each threshold level
Fig. 9.

CPU time ranking of all algorithms
Table 2.
Results of SSIM measurement
| Thresholds | Image | FA | SCA | SSO | VPL | WOA | VPLWOA |
|---|---|---|---|---|---|---|---|
| 2 | Img1 | 0.62007 | 0.63155 | 0.62947 | 0.64640 | 0.63715 | 0.63186 |
| Img2 | 0.55168 | 0.55300 | 0.54803 | 0.55257 | 0.56523 | 0.55384 | |
| Img3 | 0.54377 | 0.53753 | 0.54016 | 0.53564 | 0.54395 | 0.53245 | |
| Img4 | 0.52383 | 0.54937 | 0.52714 | 0.53655 | 0.54037 | 0.52874 | |
| Img5 | 0.59020 | 0.56884 | 0.57902 | 0.57992 | 0.58575 | 0.57883 | |
| Img6 | 0.64846 | 0.63458 | 0.62959 | 0.64663 | 0.64851 | 0.65495 | |
| Img7 | 0.60689 | 0.60665 | 0.61443 | 0.60847 | 0.61138 | 0.61210 | |
| Img8 | 0.56698 | 0.54439 | 0.55416 | 0.54765 | 0.54701 | 0.55928 | |
| Img9 | 0.52741 | 0.52098 | 0.53480 | 0.52159 | 0.52232 | 0.54442 | |
| Img10 | 0.51784 | 0.51099 | 0.50089 | 0.51950 | 0.51008 | 0.50525 | |
| Img11 | 0.58516 | 0.59776 | 0.58666 | 0.58575 | 0.59709 | 0.58516 | |
| 4 | Img1 | 0.75152 | 0.73157 | 0.73265 | 0.74466 | 0.73718 | 0.73101 |
| Img2 | 0.70734 | 0.69656 | 0.67500 | 0.69769 | 0.70686 | 0.68571 | |
| Img3 | 0.68303 | 0.66521 | 0.67242 | 0.66969 | 0.68518 | 0.66582 | |
| Img4 | 0.66515 | 0.67008 | 0.66349 | 0.64503 | 0.65041 | 0.67427 | |
| Img5 | 0.68432 | 0.69230 | 0.69433 | 0.70338 | 0.69295 | 0.70058 | |
| Img6 | 0.72783 | 0.76940 | 0.74140 | 0.72477 | 0.71779 | 0.75041 | |
| Img7 | 0.69644 | 0.69312 | 0.69607 | 0.68898 | 0.69318 | 0.69664 | |
| Img8 | 0.68544 | 0.66179 | 0.67548 | 0.67163 | 0.67151 | 0.68019 | |
| Img9 | 0.66903 | 0.65581 | 0.66893 | 0.66342 | 0.66159 | 0.66908 | |
| Img10 | 0.67230 | 0.66341 | 0.67123 | 0.67060 | 0.67279 | 0.66705 | |
| Img11 | 0.67324 | 0.67231 | 0.68064 | 0.68115 | 0.67647 | 0.66814 | |
| 6 | Img1 | 0.79139 | 0.80993 | 0.79955 | 0.80387 | 0.79338 | 0.79875 |
| Img2 | 0.78000 | 0.78954 | 0.79261 | 0.78299 | 0.78469 | 0.78459 | |
| Img3 | 0.74271 | 0.74306 | 0.75043 | 0.75201 | 0.73621 | 0.72995 | |
| Img4 | 0.76452 | 0.74915 | 0.74879 | 0.73331 | 0.74042 | 0.73414 | |
| Img5 | 0.75337 | 0.74868 | 0.74835 | 0.75195 | 0.74770 | 0.75856 | |
| Img6 | 0.78010 | 0.79715 | 0.78944 | 0.77581 | 0.75769 | 0.78408 | |
| Img7 | 0.73565 | 0.74193 | 0.73885 | 0.73971 | 0.73636 | 0.73717 | |
| Img8 | 0.74491 | 0.72207 | 0.72770 | 0.72875 | 0.73023 | 0.74149 | |
| Img9 | 0.72997 | 0.71769 | 0.72779 | 0.72180 | 0.73227 | 0.72590 | |
| Img10 | 0.74584 | 0.75258 | 0.75511 | 0.75461 | 0.75412 | 0.76505 | |
| Img11 | 0.72512 | 0.71959 | 0.71829 | 0.73485 | 0.72624 | 0.72201 | |
| 8 | Img1 | 0.83465 | 0.83274 | 0.82936 | 0.82961 | 0.83625 | 0.83236 |
| Img2 | 0.83022 | 0.81869 | 0.83049 | 0.83798 | 0.82977 | 0.83588 | |
| Img3 | 0.78725 | 0.79040 | 0.79685 | 0.79661 | 0.78906 | 0.80267 | |
| Img4 | 0.79390 | 0.79712 | 0.79315 | 0.78668 | 0.77327 | 0.79252 | |
| Img5 | 0.78530 | 0.78842 | 0.78941 | 0.78515 | 0.79004 | 0.79062 | |
| Img6 | 0.79754 | 0.79183 | 0.77495 | 0.79418 | 0.81333 | 0.80073 | |
| Img7 | 0.76955 | 0.76395 | 0.76719 | 0.76216 | 0.77385 | 0.76990 | |
| Img8 | 0.78343 | 0.78284 | 0.76606 | 0.78341 | 0.76120 | 0.76736 | |
| Img9 | 0.76176 | 0.75645 | 0.76541 | 0.77553 | 0.76999 | 0.76295 | |
| Img10 | 0.79469 | 0.79342 | 0.80503 | 0.80223 | 0.79821 | 0.80305 | |
| Img11 | 0.76679 | 0.75258 | 0.75893 | 0.75663 | 0.75419 | 0.76395 | |
| 10 | Img1 | 0.85393 | 0.85126 | 0.86114 | 0.85099 | 0.85786 | 0.85692 |
| Img2 | 0.86085 | 0.85327 | 0.86212 | 0.86015 | 0.86448 | 0.84318 | |
| Img3 | 0.82542 | 0.80763 | 0.81514 | 0.82625 | 0.81150 | 0.81515 | |
| Img4 | 0.81674 | 0.81181 | 0.80371 | 0.80668 | 0.81400 | 0.80677 | |
| Img5 | 0.81139 | 0.81460 | 0.81419 | 0.80777 | 0.80816 | 0.80845 | |
| Img6 | 0.83596 | 0.82182 | 0.83152 | 0.82765 | 0.83215 | 0.83299 | |
| Img7 | 0.78608 | 0.79426 | 0.78940 | 0.79323 | 0.79614 | 0.81313 | |
| Img8 | 0.79260 | 0.77799 | 0.80316 | 0.81062 | 0.81100 | 0.80267 | |
| Img9 | 0.78946 | 0.79534 | 0.80092 | 0.79660 | 0.80563 | 0.79799 | |
| Img10 | 0.83321 | 0.84227 | 0.83723 | 0.83698 | 0.83503 | 0.84430 | |
| Img11 | 0.78419 | 0.77809 | 0.77896 | 0.78340 | 0.77011 | 0.78662 | |
| 16 | Img1 | 0.90309 | 0.89723 | 0.89111 | 0.90074 | 0.89362 | 0.89316 |
| Img2 | 0.90714 | 0.90743 | 0.90890 | 0.88984 | 0.91142 | 0.90814 | |
| Img3 | 0.89022 | 0.87489 | 0.88257 | 0.87913 | 0.87152 | 0.88039 | |
| Img4 | 0.87810 | 0.88037 | 0.87324 | 0.88613 | 0.87160 | 0.87360 | |
| Img5 | 0.86509 | 0.85639 | 0.86148 | 0.86612 | 0.86943 | 0.86321 | |
| Img6 | 0.85456 | 0.85087 | 0.85834 | 0.86093 | 0.84822 | 0.85379 | |
| Img7 | 0.84555 | 0.84044 | 0.84054 | 0.84534 | 0.84466 | 0.84682 | |
| Img8 | 0.85458 | 0.85425 | 0.85009 | 0.84894 | 0.85948 | 0.86234 | |
| Img9 | 0.85912 | 0.84753 | 0.86324 | 0.86138 | 0.85539 | 0.84868 | |
| Img10 | 0.89768 | 0.89241 | 0.89531 | 0.89361 | 0.89658 | 0.89853 | |
| Img11 | 0.83583 | 0.83681 | 0.83795 | 0.83971 | 0.84713 | 0.84060 | |
| 18 | Img1 | 0.89989 | 0.90440 | 0.90409 | 0.90427 | 0.90525 | 0.89976 |
| Img2 | 0.91568 | 0.91765 | 0.92067 | 0.91541 | 0.91283 | 0.92272 | |
| Img3 | 0.88911 | 0.89435 | 0.89316 | 0.88739 | 0.88993 | 0.88571 | |
| Img4 | 0.88548 | 0.87562 | 0.87823 | 0.88102 | 0.88474 | 0.89268 | |
| Img5 | 0.87071 | 0.87146 | 0.88009 | 0.86997 | 0.87076 | 0.87427 | |
| Img6 | 0.85141 | 0.85844 | 0.86367 | 0.86135 | 0.86176 | 0.88035 | |
| Img7 | 0.86011 | 0.84889 | 0.85520 | 0.85587 | 0.85473 | 0.85340 | |
| Img8 | 0.86045 | 0.86248 | 0.86570 | 0.86360 | 0.86810 | 0.86159 | |
| Img9 | 0.86652 | 0.86377 | 0.87029 | 0.86366 | 0.85799 | 0.87157 | |
| Img10 | 0.90457 | 0.90303 | 0.90631 | 0.90356 | 0.89989 | 0.90686 | |
| Img11 | 0.85625 | 0.85331 | 0.84847 | 0.84114 | 0.85254 | 0.84888 | |
| 20 | Img1 | 0.91490 | 0.90339 | 0.91016 | 0.91534 | 0.90493 | 0.90802 |
| Img2 | 0.92091 | 0.91383 | 0.93098 | 0.92135 | 0.93193 | 0.92561 | |
| Img3 | 0.89921 | 0.91193 | 0.90325 | 0.88678 | 0.89498 | 0.88790 | |
| Img4 | 0.89685 | 0.88324 | 0.89057 | 0.88823 | 0.89949 | 0.89371 | |
| Img5 | 0.87979 | 0.88946 | 0.88626 | 0.88296 | 0.87717 | 0.87991 | |
| Img6 | 0.88307 | 0.86524 | 0.87218 | 0.86817 | 0.87648 | 0.86861 | |
| Img7 | 0.86612 | 0.85758 | 0.86956 | 0.85634 | 0.86260 | 0.87039 | |
| Img8 | 0.88052 | 0.88322 | 0.87936 | 0.87173 | 0.87383 | 0.87501 | |
| Img9 | 0.88274 | 0.87620 | 0.88605 | 0.87728 | 0.88568 | 0.88642 | |
| Img10 | 0.91520 | 0.91304 | 0.91879 | 0.91296 | 0.91590 | 0.91466 | |
| Img11 | 0.86196 | 0.86802 | 0.84826 | 0.85719 | 0.85733 | 0.87540 | |
| Mean | 0.78340 | 0.78060 | 0.78217 | 0.78170 | 0.78201 | 0.78341 |
Table 3.
Results of the fitness value for all algorithms
| Thresholds | Image | FA | SCA | SSO | VPL | WOA | VPLWOA |
|---|---|---|---|---|---|---|---|
| 2 | Img1 | 1703.456 | 1712.468 | 1711.894 | 1734.926 | 1725.392 | 1713.615 |
| Img2 | 1708.328 | 1687.862 | 1725.929 | 1711.276 | 1729.670 | 1713.464 | |
| Img3 | 1724.513 | 1694.385 | 1713.239 | 1708.673 | 1733.949 | 1736.985 | |
| Img4 | 1724.520 | 1726.138 | 1714.449 | 1701.156 | 1698.402 | 1722.211 | |
| Img5 | 4991.201 | 4950.548 | 4962.917 | 4983.714 | 5001.077 | 4984.048 | |
| Img6 | 1581.792 | 1587.016 | 1588.829 | 1586.535 | 1585.781 | 1584.810 | |
| Img7 | 1581.144 | 1582.674 | 1585.659 | 1584.588 | 1583.912 | 1590.158 | |
| Img8 | 1589.786 | 1579.850 | 1580.631 | 1583.905 | 1585.623 | 1589.878 | |
| Img9 | 1584.106 | 1583.971 | 1586.660 | 1593.023 | 1583.499 | 1584.887 | |
| Img10 | 1588.729 | 1583.783 | 1585.024 | 1590.103 | 1582.797 | 1585.010 | |
| Img11 | 1579.357 | 1584.041 | 1578.944 | 1576.600 | 1588.166 | 1580.550 | |
| 4 | Img1 | 1880.266 | 1875.024 | 1863.270 | 1873.830 | 1878.473 | 1864.501 |
| Img2 | 1883.126 | 1873.014 | 1872.826 | 1878.365 | 1878.864 | 1873.284 | |
| Img3 | 1891.211 | 1865.781 | 1881.080 | 1870.542 | 1875.042 | 1872.578 | |
| Img4 | 1874.896 | 1875.750 | 1869.678 | 1875.425 | 1879.000 | 1881.252 | |
| Img5 | 5216.947 | 5218.272 | 5224.690 | 5233.415 | 5222.599 | 5238.445 | |
| Img6 | 1646.383 | 1648.282 | 1649.349 | 1645.340 | 1641.283 | 1649.298 | |
| Img7 | 1642.318 | 1645.523 | 1646.438 | 1643.822 | 1647.067 | 1647.473 | |
| Img8 | 1645.481 | 1643.398 | 1646.144 | 1644.864 | 1644.308 | 1651.244 | |
| Img9 | 1645.896 | 1642.698 | 1649.793 | 1648.858 | 1647.242 | 1650.972 | |
| Img10 | 1645.121 | 1639.877 | 1646.028 | 1644.678 | 1645.269 | 1648.037 | |
| Img11 | 1646.481 | 1646.782 | 1639.757 | 1648.802 | 1644.731 | 1646.305 | |
| 6 | Img1 | 1936.724 | 1943.265 | 1946.757 | 1935.825 | 1932.088 | 1940.910 |
| Img2 | 1937.723 | 1940.812 | 1933.451 | 1934.636 | 1937.021 | 1942.985 | |
| Img3 | 1939.130 | 1940.977 | 1943.996 | 1944.390 | 1938.656 | 1944.699 | |
| Img4 | 1949.749 | 1938.982 | 1942.062 | 1939.091 | 1929.229 | 1933.273 | |
| Img5 | 5320.981 | 5314.785 | 5324.966 | 5322.433 | 5314.672 | 5326.078 | |
| Img6 | 1669.798 | 1667.301 | 1670.316 | 1668.778 | 1670.771 | 1671.528 | |
| Img7 | 1670.176 | 1670.114 | 1668.018 | 1669.107 | 1667.986 | 1668.906 | |
| Img8 | 1671.052 | 1667.890 | 1665.367 | 1669.956 | 1668.178 | 1669.466 | |
| Img9 | 1670.098 | 1668.495 | 1671.635 | 1667.210 | 1670.245 | 1669.733 | |
| Img10 | 1667.459 | 1668.249 | 1670.933 | 1671.194 | 1670.717 | 1672.183 | |
| Img11 | 1669.845 | 1666.510 | 1668.733 | 1670.057 | 1670.452 | 1669.176 | |
| 8 | Img1 | 1969.910 | 1969.996 | 1971.522 | 1965.633 | 1971.525 | 1979.465 |
| Img2 | 1969.583 | 1969.388 | 1977.017 | 1977.974 | 1976.591 | 1967.421 | |
| Img3 | 1979.697 | 1973.113 | 1965.554 | 1978.375 | 1966.828 | 1976.470 | |
| Img4 | 1977.538 | 1969.431 | 1974.153 | 1970.882 | 1967.643 | 1973.971 | |
| Img5 | 5372.387 | 5368.011 | 5368.828 | 5362.795 | 5369.879 | 5373.830 | |
| Img6 | 1681.891 | 1682.540 | 1681.386 | 1681.988 | 1682.062 | 1681.316 | |
| Img7 | 1681.365 | 1679.654 | 1681.552 | 1680.014 | 1683.024 | 1680.958 | |
| Img8 | 1682.874 | 1681.450 | 1681.727 | 1681.702 | 1680.891 | 1680.439 | |
| Img9 | 1680.004 | 1678.793 | 1681.110 | 1683.465 | 1681.823 | 1682.041 | |
| Img10 | 1682.271 | 1678.720 | 1682.618 | 1682.315 | 1680.996 | 1682.159 | |
| Img11 | 1682.297 | 1682.160 | 1681.707 | 1680.938 | 1682.940 | 1680.916 | |
| 10 | Img1 | 1990.431 | 1988.302 | 1992.985 | 1992.739 | 1988.937 | 1995.718 |
| Img2 | 1989.846 | 1989.727 | 1991.627 | 1987.391 | 1993.901 | 1987.550 | |
| Img3 | 1991.617 | 1982.272 | 1989.948 | 1991.725 | 1987.954 | 1983.224 | |
| Img4 | 1992.034 | 1990.704 | 1987.544 | 1991.167 | 1989.722 | 1991.375 | |
| Img5 | 5394.623 | 5392.315 | 5399.817 | 5392.619 | 5392.841 | 5397.687 | |
| Img6 | 1689.660 | 1688.722 | 1689.179 | 1689.525 | 1689.656 | 1689.690 | |
| Img7 | 1686.208 | 1688.681 | 1688.886 | 1688.607 | 1689.402 | 1689.058 | |
| Img8 | 1690.424 | 1685.208 | 1688.664 | 1688.127 | 1689.522 | 1687.526 | |
| Img9 | 1687.180 | 1688.590 | 1687.812 | 1687.531 | 1689.867 | 1687.390 | |
| Img10 | 1690.395 | 1688.587 | 1688.781 | 1688.665 | 1688.690 | 1688.352 | |
| Img11 | 1687.900 | 1687.781 | 1689.748 | 1688.661 | 1687.864 | 1688.373 | |
| 16 | Img1 | 2016.800 | 2013.430 | 2017.447 | 2017.023 | 2016.951 | 2015.364 |
| Img2 | 2016.590 | 2015.907 | 2016.962 | 2012.270 | 2018.092 | 2017.226 | |
| Img3 | 2018.654 | 2018.339 | 2018.765 | 2019.093 | 2017.148 | 2017.648 | |
| Img4 | 2018.135 | 2016.896 | 2016.444 | 2018.430 | 2017.962 | 2015.885 | |
| Img5 | 5438.271 | 5433.432 | 5437.368 | 5437.218 | 5438.574 | 5437.083 | |
| Img6 | 1697.317 | 1696.644 | 1698.112 | 1697.936 | 1697.921 | 1698.410 | |
| Img7 | 1698.651 | 1698.606 | 1698.342 | 1698.515 | 1698.717 | 1698.737 | |
| Img8 | 1698.501 | 1697.873 | 1698.916 | 1698.827 | 1697.757 | 1697.058 | |
| Img9 | 1698.529 | 1696.035 | 1698.576 | 1698.087 | 1697.421 | 1697.605 | |
| Img10 | 1698.305 | 1698.054 | 1697.960 | 1697.835 | 1698.562 | 1698.233 | |
| Img11 | 1697.598 | 1697.661 | 1698.475 | 1699.315 | 1698.596 | 1697.381 | |
| 18 | Img1 | 2018.848 | 2020.102 | 2020.419 | 2019.776 | 2023.681 | 2020.558 |
| Img2 | 2021.382 | 2020.628 | 2022.967 | 2020.404 | 2018.636 | 2022.772 | |
| Img3 | 2021.335 | 2021.488 | 2022.468 | 2020.472 | 2021.385 | 2019.220 | |
| Img4 | 2021.508 | 2018.974 | 2020.616 | 2020.838 | 2021.338 | 2022.868 | |
| Img5 | 5439.587 | 5442.411 | 5445.801 | 5439.403 | 5444.172 | 5441.609 | |
| Img6 | 1700.246 | 1699.000 | 1699.802 | 1698.880 | 1700.041 | 1700.336 | |
| Img7 | 1700.496 | 1699.619 | 1699.874 | 1699.989 | 1700.016 | 1699.656 | |
| Img8 | 1699.626 | 1698.794 | 1699.347 | 1699.707 | 1700.438 | 1699.196 | |
| Img9 | 1699.056 | 1699.161 | 1700.094 | 1699.321 | 1700.025 | 1698.867 | |
| Img10 | 1700.230 | 1700.155 | 1699.514 | 1699.738 | 1699.900 | 1698.842 | |
| Img11 | 1700.575 | 1699.832 | 1699.939 | 1699.511 | 1700.258 | 1699.678 | |
| 20 | Img1 | 2024.802 | 2022.751 | 2023.736 | 2023.926 | 2024.863 | 2026.248 |
| Img2 | 2024.885 | 2021.444 | 2025.606 | 2025.655 | 2025.529 | 2022.107 | |
| Img3 | 2024.421 | 2020.847 | 2020.286 | 2022.098 | 2021.090 | 2026.276 | |
| Img4 | 2025.917 | 2020.931 | 2024.377 | 2021.573 | 2022.553 | 2024.495 | |
| Img5 | 5447.912 | 5447.243 | 5445.748 | 5448.770 | 5445.784 | 5442.893 | |
| Img6 | 1701.980 | 1700.648 | 1700.412 | 1700.950 | 1701.446 | 1700.980 | |
| Img7 | 1701.476 | 1700.213 | 1701.468 | 1701.583 | 1700.594 | 1701.904 | |
| Img8 | 1700.864 | 1701.527 | 1701.106 | 1701.463 | 1701.016 | 1700.868 | |
| Img9 | 1701.278 | 1701.106 | 1701.605 | 1700.433 | 1701.487 | 1701.386 | |
| Img10 | 1700.953 | 1701.042 | 1701.736 | 1700.214 | 1700.238 | 1700.895 | |
| Img11 | 1700.270 | 1701.583 | 1701.006 | 1701.040 | 1701.172 | 1701.721 | |
| Mean | 2103.442 | 2100.921 | 2102.806 | 2102.821 | 2103.160 | 2103.714 |
Table 4 whereas, Fig. 3 shows a sample of a segmented image and its histogram with the corresponding thresholds at level 8. The results of the PSNR measurement are listed in Table 1 and Fig. 4. As shown in this table, VPLWOA has achieved the best results in 26 cases out of 88 (11 images × eight thresholds), followed by SSO (with 15 cases), WOA (13 cases), VPL (12 cases), FA (12 cases), and SCA (10 cases). Moreover, the VPLWOA has obtained the best PSNR values in most images in six thresholds out of eight (i.e., two, four, eight, 10, 18, and 20); whereas, in thresholds six and 16, it performed equally with SSO, VPL, and WOA. In addition, Fig. 4 illustrates the PSNR ranking of the algorithms overall thresholds and images. The proposed VPLWOA method is better than the other algorithms, whereas Fig. 5 shows the average of the PSNR values for all algorithms at each threshold level.
Table 4.
CPU time was obtained by each algorithm
| Thresholds | Image | FA | SCA | SSO | VPL | WOA | VPLWOA |
|---|---|---|---|---|---|---|---|
| 2 | Img1 | 0.2022 | 0.2045 | 0.2103 | 0.6251 | 0.1869 | 0.4105 |
| Img2 | 0.1953 | 0.2419 | 0.2003 | 0.5627 | 0.1760 | 0.4746 | |
| Img3 | 0.3379 | 1.5403 | 1.1506 | 1.2506 | 0.3920 | 1.1734 | |
| Img4 | 0.7806 | 0.7262 | 0.5917 | 0.7442 | 1.2155 | 0.6172 | |
| Img5 | 0.3423 | 0.4351 | 0.2391 | 0.5371 | 0.3206 | 0.4052 | |
| Img6 | 0.6497 | 0.3231 | 0.4015 | 0.5168 | 0.5045 | 0.3866 | |
| Img7 | 0.4918 | 0.4501 | 0.3458 | 0.5368 | 1.9572 | 0.4037 | |
| Img8 | 0.3049 | 0.3035 | 0.2941 | 0.5252 | 0.2966 | 0.3987 | |
| Img9 | 0.3089 | 0.3075 | 0.2981 | 0.7579 | 0.2953 | 0.5518 | |
| Img10 | 0.3028 | 0.3007 | 0.2942 | 0.5197 | 0.2919 | 0.3492 | |
| Img11 | 0.3058 | 0.3033 | 0.2993 | 0.4999 | 0.2918 | 0.2857 | |
| 4 | Img1 | 0.2727 | 0.2420 | 0.2039 | 0.4771 | 0.2032 | 0.3827 |
| Img2 | 0.2036 | 0.2116 | 0.2131 | 0.6500 | 0.2158 | 0.4677 | |
| Img3 | 0.2373 | 0.3730 | 0.2163 | 0.3901 | 0.2793 | 0.2640 | |
| Img4 | 0.2873 | 1.5276 | 0.1734 | 0.4766 | 0.4261 | 0.3385 | |
| Img5 | 1.5127 | 1.3529 | 0.9766 | 1.2575 | 0.8781 | 1.1817 | |
| Img6 | 0.5174 | 0.5886 | 0.3999 | 0.6302 | 0.3849 | 0.4758 | |
| Img7 | 2.2474 | 0.7447 | 0.6062 | 0.8582 | 0.6320 | 0.7324 | |
| Img8 | 0.3343 | 0.3186 | 0.3128 | 0.7674 | 0.3111 | 0.5785 | |
| Img9 | 0.3173 | 0.3211 | 0.3111 | 0.7156 | 0.3130 | 0.5263 | |
| Img10 | 0.3259 | 0.3178 | 0.3150 | 0.7685 | 0.3034 | 0.6411 | |
| Img11 | 0.3227 | 0.3180 | 0.3183 | 0.6012 | 0.3091 | 0.4933 | |
| 6 | Img1 | 0.3110 | 0.2132 | 0.2308 | 0.6504 | 0.2147 | 0.5290 |
| Img2 | 0.2337 | 0.2310 | 0.2399 | 0.3935 | 0.2197 | 0.1784 | |
| Img3 | 0.3839 | 0.6003 | 0.3843 | 0.5104 | 0.6447 | 0.3684 | |
| Img4 | 1.1227 | 0.3617 | 0.5346 | 0.7846 | 3.5723 | 0.6594 | |
| Img5 | 0.9692 | 0.4990 | 0.3868 | 0.6362 | 0.6764 | 0.4515 | |
| Img6 | 0.4025 | 0.3859 | 0.5560 | 0.8496 | 0.6305 | 0.7230 | |
| Img7 | 0.6364 | 0.5864 | 0.3796 | 0.8673 | 0.3892 | 0.6623 | |
| Img8 | 0.3332 | 0.3333 | 0.3292 | 0.5660 | 0.3234 | 0.4685 | |
| Img9 | 0.3326 | 0.3353 | 0.3230 | 0.5240 | 0.3231 | 0.3988 | |
| Img10 | 0.3335 | 0.3318 | 0.3231 | 0.6570 | 0.3466 | 0.4494 | |
| Img11 | 0.3346 | 0.3372 | 0.3200 | 0.6295 | 0.3228 | 0.4821 | |
| 8 | Img1 | 0.2406 | 0.2516 | 0.2383 | 0.4037 | 0.2264 | 0.3201 |
| Img2 | 0.2300 | 0.2488 | 0.2319 | 0.5264 | 0.2267 | 0.3461 | |
| Img3 | 0.5868 | 0.2019 | 0.2278 | 0.5262 | 0.5714 | 0.4555 | |
| Img4 | 0.7221 | 1.6001 | 1.3738 | 1.8111 | 0.7654 | 1.2506 | |
| Img5 | 0.8904 | 1.7213 | 1.1490 | 1.5715 | 0.6922 | 1.3579 | |
| Img6 | 0.4337 | 0.8156 | 0.5367 | 0.9798 | 0.5664 | 0.8502 | |
| Img7 | 0.8669 | 1.0865 | 0.4703 | 0.8142 | 0.8047 | 0.6345 | |
| Img8 | 0.3413 | 0.3425 | 0.3333 | 0.6596 | 0.3398 | 0.4869 | |
| Img9 | 0.3503 | 0.3473 | 0.3356 | 0.6804 | 0.3330 | 0.4636 | |
| Img10 | 0.3441 | 0.3510 | 0.3420 | 0.4832 | 0.3337 | 0.3827 | |
| Img11 | 0.3487 | 0.3514 | 0.3433 | 0.5066 | 0.3420 | 0.3476 | |
| 10 | Img1 | 0.2390 | 0.2426 | 0.2528 | 0.7334 | 0.2388 | 0.4602 |
| Img2 | 0.2675 | 0.2292 | 0.2513 | 0.4554 | 0.2355 | 0.1737 | |
| Img3 | 0.5649 | 0.2682 | 0.4288 | 0.7347 | 0.8408 | 0.4058 | |
| Img4 | 1.2186 | 1.5791 | 0.6133 | 0.9679 | 1.7173 | 0.6544 | |
| Img5 | 0.3093 | 0.3412 | 0.2778 | 0.5382 | 0.4382 | 0.2222 | |
| Img6 | 0.6658 | 0.5761 | 0.6460 | 0.9406 | 0.6861 | 0.6368 | |
| Img7 | 0.5375 | 0.4684 | 0.4356 | 0.8357 | 1.6676 | 0.4938 | |
| Img8 | 0.3611 | 0.3589 | 0.3502 | 0.5007 | 0.3500 | 0.1727 | |
| Img9 | 0.3601 | 0.3655 | 0.3507 | 0.4679 | 0.3480 | 0.1852 | |
| Img10 | 0.3610 | 0.3659 | 0.3545 | 0.6028 | 0.3559 | 0.2790 | |
| Img11 | 0.3626 | 0.3627 | 0.3491 | 0.7264 | 0.3551 | 0.4327 | |
| 16 | Img1 | 0.3089 | 0.3109 | 0.2693 | 0.7436 | 0.2640 | 0.4344 |
| Img2 | 0.3954 | 0.4252 | 0.3583 | 0.6493 | 0.3070 | 0.3879 | |
| Img3 | 0.6055 | 1.0184 | 0.7830 | 0.9346 | 0.4263 | 0.6527 | |
| Img4 | 1.5707 | 1.3989 | 2.7816 | 4.0752 | 2.5318 | 3.7630 | |
| Img5 | 0.9095 | 0.5433 | 2.5066 | 1.9848 | 0.3279 | 1.6453 | |
| Img6 | 1.1070 | 1.9950 | 0.6404 | 0.8875 | 2.3921 | 0.5411 | |
| Img7 | 0.3927 | 0.4389 | 0.4030 | 0.6344 | 0.3918 | 0.3824 | |
| Img8 | 0.3984 | 0.4155 | 0.3900 | 0.7991 | 0.3955 | 0.5381 | |
| Img9 | 0.4024 | 0.4086 | 0.3970 | 0.6159 | 0.3927 | 0.3256 | |
| Img10 | 0.3904 | 0.4331 | 0.3885 | 0.5596 | 0.3945 | 0.2999 | |
| Img11 | 0.4108 | 0.4207 | 0.3908 | 0.7671 | 0.4042 | 0.4878 | |
| 18 | Img1 | 0.2957 | 0.3210 | 0.2701 | 0.4757 | 0.2695 | 0.1578 |
| Img2 | 0.2994 | 0.3032 | 0.2654 | 0.5485 | 0.2983 | 0.2006 | |
| Img3 | 0.8833 | 0.6712 | 0.6500 | 1.0875 | 0.5037 | 0.7975 | |
| Img4 | 1.7662 | 1.5250 | 2.8344 | 3.2870 | 0.9450 | 2.5549 | |
| Img5 | 0.6127 | 4.5505 | 5.8708 | 6.2508 | 0.2685 | 4.9877 | |
| Img6 | 0.9035 | 0.8290 | 0.7067 | 1.1090 | 1.3385 | 0.7745 | |
| Img7 | 0.4038 | 0.4271 | 0.4048 | 0.8946 | 0.4105 | 0.6213 | |
| Img8 | 0.4227 | 0.4343 | 0.4173 | 0.6782 | 0.4078 | 0.4214 | |
| Img9 | 0.4103 | 0.4324 | 0.4062 | 0.5587 | 0.4072 | 0.2756 | |
| Img10 | 0.4163 | 0.4385 | 0.3972 | 0.7871 | 0.4028 | 0.4796 | |
| Img11 | 0.4225 | 0.4295 | 0.4045 | 0.8643 | 0.4116 | 0.6006 | |
| 20 | Img1 | 0.3472 | 0.3427 | 0.2971 | 0.4654 | 0.3163 | 0.1286 |
| Img2 | 0.3824 | 1.7523 | 0.3089 | 0.4261 | 0.5682 | 0.1432 | |
| Img3 | 12.6460 | 1.9598 | 2.7243 | 3.0159 | 1.4341 | 2.7171 | |
| Img4 | 0.6017 | 2.3836 | 0.4317 | 0.5692 | 0.6093 | 0.2761 | |
| Img5 | 0.3827 | 0.5513 | 0.4618 | 0.8218 | 0.4369 | 0.5457 | |
| Img6 | 1.0707 | 0.5798 | 2.9782 | 2.4591 | 0.7232 | 1.1108 | |
| Img7 | 0.4296 | 0.4432 | 0.4131 | 0.6962 | 0.4200 | 0.3496 | |
| Img8 | 0.4190 | 0.4399 | 0.4183 | 0.7330 | 0.4238 | 0.3882 | |
| Img9 | 0.4187 | 0.4396 | 0.4160 | 0.5426 | 0.4194 | 0.2474 | |
| Img10 | 0.4288 | 0.4502 | 0.4354 | 0.7329 | 0.4180 | 0.4498 | |
| Img11 | 0.4232 | 0.4501 | 0.4221 | 0.6891 | 0.4420 | 0.4384 | |
| Mean | 0.6599 | 0.6376 | 0.6081 | 0.8926 | 0.5726 | 0.6369 |
Fig. 3.
Results of histogram and corresponding thresholds over a segmented image at threshold eight. a FA, b SCA, c SSO, d VPL, e WOA, f VPLWOA
Table 1.
Results of the PSNR measurement
| Thresholds | Image | FA | SCA | SSO | VPL | WOA | VPLWOA |
|---|---|---|---|---|---|---|---|
| 2 | Img1 | 16.9862 | 16.8935 | 17.1603 | 17.3468 | 17.1875 | 17.0841 |
| Img2 | 13.2816 | 13.6248 | 13.3721 | 13.4621 | 13.7191 | 13.6955 | |
| Img3 | 14.7014 | 14.6223 | 14.6354 | 14.5269 | 14.8620 | 14.5815 | |
| Img4 | 15.4938 | 15.5432 | 15.0432 | 15.2320 | 15.2529 | 15.2961 | |
| Img5 | 14.8236 | 14.2742 | 14.2438 | 14.5781 | 14.5772 | 14.4622 | |
| Img6 | 10.8031 | 10.3949 | 10.2884 | 10.6508 | 10.7562 | 10.9401 | |
| Img7 | 14.1213 | 14.2473 | 14.4905 | 14.0071 | 14.4507 | 14.2719 | |
| Img8 | 13.3395 | 12.6509 | 12.8209 | 13.0921 | 12.6868 | 13.0681 | |
| Img9 | 15.0914 | 14.9508 | 15.1863 | 14.8873 | 14.7754 | 15.5376 | |
| Img10 | 14.0840 | 13.9958 | 13.7820 | 13.7806 | 14.0249 | 14.2581 | |
| Img11 | 14.5445 | 14.8750 | 14.5309 | 14.8307 | 14.5633 | 14.0745 | |
| 4 | Img1 | 19.6342 | 19.7965 | 19.9100 | 19.9361 | 19.9437 | 20.2089 |
| Img2 | 16.3032 | 16.3605 | 15.9675 | 16.8962 | 16.5774 | 16.7006 | |
| Img3 | 18.6885 | 17.7943 | 18.2413 | 17.8756 | 18.0391 | 17.5693 | |
| Img4 | 17.9319 | 18.3011 | 18.2807 | 17.8867 | 17.6242 | 18.4572 | |
| Img5 | 17.6923 | 17.4820 | 17.9605 | 18.2067 | 17.9319 | 17.8631 | |
| Img6 | 13.6680 | 15.0067 | 13.9716 | 13.2850 | 13.5077 | 15.0171 | |
| Img7 | 17.5034 | 17.3859 | 17.8057 | 17.9000 | 17.8836 | 17.0503 | |
| Img8 | 16.1245 | 16.5052 | 15.7997 | 15.3265 | 15.3318 | 16.6781 | |
| Img9 | 18.7365 | 18.2300 | 18.7015 | 18.5667 | 18.4587 | 18.6853 | |
| Img10 | 17.4172 | 17.1563 | 17.2624 | 17.2452 | 17.4938 | 17.0338 | |
| Img11 | 17.7822 | 17.9915 | 18.3657 | 18.2104 | 18.0186 | 17.9002 | |
| 6 | Img1 | 21.8711 | 22.1926 | 22.3355 | 22.0531 | 21.7297 | 22.2850 |
| Img2 | 19.0305 | 19.5836 | 18.3253 | 19.0123 | 19.4015 | 19.2176 | |
| Img3 | 19.7792 | 19.9261 | 19.9955 | 20.1673 | 20.2162 | 19.4665 | |
| Img4 | 20.4034 | 20.3900 | 20.2203 | 20.5867 | 20.4517 | 20.1880 | |
| Img5 | 20.3119 | 19.8147 | 19.5662 | 19.9159 | 19.7799 | 20.1632 | |
| Img6 | 16.6484 | 18.0173 | 17.5689 | 16.3299 | 15.5464 | 16.7274 | |
| Img7 | 19.3891 | 19.7564 | 19.1947 | 19.7649 | 19.4240 | 20.0239 | |
| Img8 | 18.1171 | 18.1848 | 18.4227 | 17.5898 | 17.8169 | 18.1277 | |
| Img9 | 20.5292 | 20.2279 | 20.4146 | 20.2544 | 20.7545 | 20.4219 | |
| Img10 | 19.0979 | 19.5323 | 19.5047 | 19.7654 | 19.4606 | 19.7980 | |
| Img11 | 20.5565 | 19.9965 | 19.6923 | 20.9513 | 20.1597 | 20.0072 | |
| 8 | Img1 | 23.4005 | 23.6178 | 23.4981 | 23.2342 | 23.8442 | 24.0403 |
| Img2 | 21.0204 | 20.3202 | 20.4069 | 20.9336 | 20.8015 | 21.1191 | |
| Img3 | 21.5551 | 21.6998 | 21.6198 | 21.8398 | 21.1747 | 22.0062 | |
| Img4 | 21.8089 | 21.6952 | 21.8598 | 21.5358 | 21.6700 | 22.2265 | |
| Img5 | 21.7953 | 21.6565 | 21.4703 | 21.5033 | 21.6945 | 21.6175 | |
| Img6 | 18.9127 | 18.9125 | 18.1487 | 18.3825 | 19.7630 | 18.5474 | |
| Img7 | 20.8264 | 21.8325 | 21.3857 | 21.5586 | 21.5723 | 21.1429 | |
| Img8 | 19.8939 | 20.4165 | 19.7376 | 20.8707 | 20.1677 | 19.8744 | |
| Img9 | 21.9230 | 21.6003 | 21.7185 | 22.1995 | 21.9198 | 21.9226 | |
| Img10 | 20.6575 | 20.7922 | 21.1773 | 20.8688 | 21.1152 | 21.0868 | |
| Img11 | 22.4731 | 21.5464 | 21.9168 | 21.8332 | 21.2763 | 21.3172 | |
| 10 | Img1 | 24.9131 | 24.6436 | 25.1112 | 25.1223 | 24.7852 | 25.2767 |
| Img2 | 22.9298 | 22.3258 | 22.2202 | 21.6003 | 21.8324 | 21.8329 | |
| Img3 | 22.8483 | 22.7410 | 22.8056 | 22.8915 | 23.0721 | 23.2224 | |
| Img4 | 22.8853 | 22.2719 | 23.0292 | 22.6176 | 23.0109 | 22.5664 | |
| Img5 | 22.5748 | 22.7365 | 22.7957 | 22.7754 | 22.6471 | 23.0254 | |
| Img6 | 20.4181 | 20.7873 | 21.6068 | 21.0494 | 20.3512 | 20.4688 | |
| Img7 | 22.4259 | 23.2611 | 22.9225 | 22.9851 | 23.0355 | 22.8292 | |
| Img8 | 21.5567 | 20.9912 | 21.7195 | 21.7886 | 21.8700 | 21.7690 | |
| Img9 | 22.9021 | 23.1008 | 23.3730 | 23.1387 | 23.4843 | 23.2412 | |
| Img10 | 22.7883 | 22.8892 | 22.4168 | 22.5975 | 22.3539 | 22.4242 | |
| Img11 | 23.3315 | 22.7852 | 22.9233 | 23.4181 | 22.4418 | 23.3100 | |
| 16 | Img1 | 27.6762 | 27.2667 | 27.5283 | 27.3741 | 27.5076 | 27.0934 |
| Img2 | 25.0974 | 25.2490 | 25.2954 | 24.5264 | 25.2225 | 24.9576 | |
| Img3 | 26.2217 | 26.1339 | 26.3436 | 26.1970 | 26.2373 | 25.9069 | |
| Img4 | 25.7223 | 25.8743 | 25.8358 | 26.5395 | 25.9065 | 25.7018 | |
| Img5 | 25.8069 | 25.4509 | 25.6042 | 25.8854 | 26.1860 | 25.7348 | |
| Img6 | 24.0556 | 24.5077 | 24.1605 | 24.6704 | 22.5051 | 24.1373 | |
| Img7 | 25.8530 | 25.8553 | 25.6168 | 25.7108 | 26.1082 | 26.2627 | |
| Img8 | 25.3821 | 24.9393 | 24.5859 | 25.3535 | 25.1894 | 24.6683 | |
| Img9 | 26.0149 | 25.6271 | 25.7360 | 26.3322 | 26.0496 | 26.5161 | |
| Img10 | 25.8328 | 26.0055 | 25.7168 | 25.5605 | 25.6689 | 25.4011 | |
| Img11 | 25.8789 | 25.9319 | 25.7039 | 25.7906 | 26.5908 | 26.2482 | |
| 18 | Img1 | 27.7591 | 27.9813 | 27.8874 | 27.8711 | 28.5719 | 27.9615 |
| Img2 | 26.3565 | 26.3264 | 26.6271 | 25.8362 | 25.8313 | 25.3133 | |
| Img3 | 26.6226 | 26.7536 | 27.2143 | 26.6853 | 26.3976 | 26.8314 | |
| Img4 | 26.9177 | 25.9322 | 26.5718 | 26.4380 | 26.3406 | 26.9832 | |
| Img5 | 26.2371 | 26.1858 | 26.9611 | 26.5100 | 26.5049 | 26.2094 | |
| Img6 | 24.5866 | 24.4716 | 23.8208 | 24.5621 | 24.3140 | 24.9845 | |
| Img7 | 27.0527 | 25.9377 | 26.7618 | 26.9897 | 26.5329 | 26.1927 | |
| Img8 | 25.9400 | 25.7817 | 25.5159 | 25.4062 | 26.4015 | 25.6718 | |
| Img9 | 26.7999 | 26.5582 | 26.9210 | 26.5695 | 26.1238 | 26.9544 | |
| Img10 | 26.1791 | 26.0432 | 26.3823 | 25.9803 | 26.1400 | 26.4556 | |
| Img11 | 27.0401 | 26.8415 | 26.7430 | 26.0961 | 27.0144 | 26.9094 | |
| 20 | Img1 | 28.8200 | 28.2206 | 28.9546 | 28.4840 | 28.9119 | 28.2841 |
| Img2 | 26.9989 | 26.5946 | 27.0054 | 27.3749 | 27.3322 | 26.5047 | |
| Img3 | 27.1811 | 27.3694 | 27.9064 | 26.9528 | 26.7792 | 27.0252 | |
| Img4 | 27.0817 | 26.2157 | 26.9658 | 26.4252 | 27.2940 | 27.4291 | |
| Img5 | 26.9088 | 27.5567 | 27.3600 | 27.5012 | 26.7439 | 26.7573 | |
| Img6 | 25.7701 | 24.9364 | 26.2360 | 25.9663 | 26.2371 | 25.2798 | |
| Img7 | 27.1759 | 26.8212 | 27.8297 | 26.7927 | 27.0538 | 27.6239 | |
| Img8 | 27.1320 | 27.3327 | 26.5732 | 26.3279 | 26.3411 | 25.5980 | |
| Img9 | 27.5672 | 27.4286 | 27.8230 | 27.2482 | 27.7252 | 27.8239 | |
| Img10 | 26.9166 | 26.8282 | 26.9848 | 27.0354 | 27.0661 | 27.2370 | |
| Img11 | 27.3730 | 27.5262 | 26.8973 | 26.9435 | 27.0785 | 27.9653 | |
| Mean | 21.8442 | 21.7820 | 21.8295 | 21.8046 | 21.7977 | 21.8449 |
Fig. 4.

PSNR ranking of all algorithms
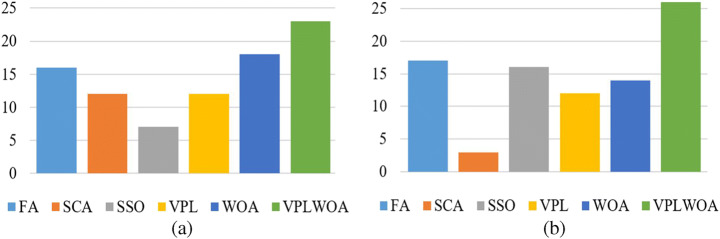
The results of the SSIM measurement are shown in Table 2 and Fig. 6 (a). As shown in the table, VPLWOA has achieved the best results in 23 cases out of 88 (11 images × 8 thresholds), followed by WOA (with 18 cases), FA (with 16 cases), SCA (with 12 cases), VPL (with 12 cases), and SSO (with seven cases). Besides, the VPLWOA has obtained the best SSIM values in most images in threshold 18 and performed equally with WOA in thresholds 10 and 16. At threshold 2, all algorithms obtained the best SSIM value in two images except for SSO. The VPLWOA and FA outperformed all other algorithms in three images for each one in thresholds four and 20. However, the best algorithms are SCA and WOA at thresholds six and eight, respectively, followed by VPLWOA, VPL, and FA. Moreover, Fig. 8(a) illustrates the SSIM ranking of the algorithms overall thresholds and images. This approach achieved better results than other algorithms, whereas, Fig. 7 shows the average of the SSIM values for all algorithms at each threshold level.
The results of the fitness value are illustrated in Table 3. As shown in the table, VPLWOA has achieved the highest fitness value in 26 cases out of 88 (11 images × eight thresholds), followed by FA (with 17 cases), SSO (with 16 cases), WOA (with 14 cases), VPL (with 12 cases), and SCA (with three cases).
The VPLWOA has obtained the high fitness values in most images in thresholds four, six, and 20 and performed equally with WOA and VPL in threshold two. In thresholds eight, 10, 16, and 18, VPLWOA performed nearly like WOA, VPL, SSO, and FA. The SSA is the worst one among all the algorithms. Figure 8 shows the average of the fitness values for all algorithms at each threshold level.
Based on these results, VPLWOA outperformed the other algorithms with 30%, 26%, and 30% for PSNR, SSIM, and fitness value, respectively, thereby indicating that the VPL is improved using WOA as a local search.
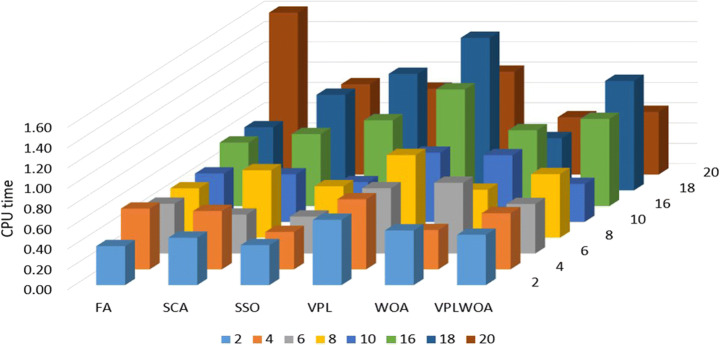
For further analysis, the CPU time results for each algorithm are recorded in Table 4. From this table, the VPLWOA achieved the best results in 21 cases and is ranked third after both WOA (with 27 cases) and SSO (with 24 cases). The SCA obtained the fourth rank (with 10 cases) followed by the FA (with 6 cases), it was ranked fifth. Whereas, the VPL was considered as the slowest algorithm in the experiments. The VPLWOA showed good CPU time in a large threshold than the smallest one.
Moreover, the results can be summarized as in Fig. 9. This figure illustrates the CPU time ranking of the algorithms overall thresholds and images. Whereas Fig. 10 shows the average of CPU time for all algorithms at each threshold level.
Fig. 10.
Average CPU time for all algorithms at each threshold level
Experimental series 2: medical images
In this experiment, the performance of the presented algorithm is assessed to determine the optimal threshold to segment a medical dataset. This dataset contains a set of lymphoblastic leukemia image database [27], which is classified into two groups (for more details, see [27]). The main task of this experiment is to segment the leukocytes (darker cells). However, this task is difficult because the blood cells do not have the same abnormalities that can influence the performance of the segmentation method. The VPLWOA is compared with the same algorithms used in previous experiments with the same parameter settings. Figure 11 shows the tested blood cell images with their histogram. These images have different characteristics.
Fig. 11.
Original and histogram of the blood cell images of leukemia image
The results of PSNR and SSIM measures of the VPLWOA method against the other methods are given in Table 5 and Figs. 12 and 13; whereas, Fig. 14 shows a sample of segmented Leukemia image and its histogram with corresponding thresholds at threshold level 8.
Table 5.
Results of blood cell segmentation
| Threshold | FA | SCA | SSO | VPL | WOA | VPLWOA | |
|---|---|---|---|---|---|---|---|
| PSNR | 2 | 17.018 | 17.724 | 18.332 | 17.369 | 17.260 | 17.910 |
| 4 | 19.567 | 19.913 | 19.813 | 20.220 | 19.093 | 20.492 | |
| 6 | 21.032 | 22.404 | 21.937 | 21.593 | 21.266 | 22.231 | |
| 8 | 21.828 | 21.563 | 23.976 | 21.878 | 23.738 | 24.384 | |
| 10 | 24.853 | 22.989 | 24.204 | 22.403 | 24.742 | 25.183 | |
| 16 | 23.764 | 24.578 | 26.263 | 23.356 | 25.584 | 26.406 | |
| 18 | 24.393 | 26.586 | 25.748 | 26.529 | 26.252 | 28.501 | |
| 20 | 25.439 | 28.892 | 27.065 | 26.098 | 27.757 | 31.292 | |
| Mean | 22.237 | 23.081 | 23.417 | 22.431 | 23.212 | 24.550 | |
| SSIM | 2 | 0.744 | 0.775 | 0.760 | 0.760 | 0.740 | 0.769 |
| 4 | 0.785 | 0.780 | 0.796 | 0.780 | 0.788 | 0.791 | |
| 6 | 0.800 | 0.805 | 0.801 | 0.804 | 0.792 | 0.802 | |
| 8 | 0.818 | 0.820 | 0.837 | 0.826 | 0.839 | 0.844 | |
| 10 | 0.846 | 0.824 | 0.832 | 0.815 | 0.799 | 0.855 | |
| 16 | 0.854 | 0.867 | 0.858 | 0.846 | 0.814 | 0.868 | |
| 18 | 0.868 | 0.844 | 0.848 | 0.855 | 0.845 | 0.887 | |
| 20 | 0.884 | 0.861 | 0.860 | 0.879 | 0.882 | 0.899 | |
| Mean | 0.8249 | 0.8220 | 0.8240 | 0.8206 | 0.8124 | 0.8394 |
Fig. 12.
Ranking of the (a) PSNR measure. (b) SSIM measure
Fig. 13.

Comparison between the VPLWOA and the other algorithms in terms of PSNR and SSIM in blood cell segmentation. a PSNR measure, b SSIM measure
Fig. 14.
Results of the histogram and corresponding thresholds over a segmented image at threshold eight. a FA, b SCA, c SSO, d VPL, e WOA, f VPLWOA
Concerning PSNR, the results illustrate that the VPLWOA has achieved the best results in 19 cases out of 48, followed by SSO with 14 cases; whereas, VPL and SCA obtained similar results (five cases for each one). The WOA came in the fifth rank with four cases, followed by FA with one case only. Moreover, the VPLWOA has the best PSNR values in threshold four and the highest threshold levels (i.e., eight, 10, 16, 18, and 20), while it came in the second rank in threshold levels two and six after SCA and SSO, respectively.
In terms of SSIM, the VPLWOA has obtained the best SSIM results in the highest threshold levels (i.e., eight, 10, 16, 18, and 20), while it came in the second rank in threshold levels two and six after SCA and four after SSO, as shown in Table 5.
Figure 12 illustrates the ranking of the algorithms overall thresholds and images for the PSNR and SSIM. As shown in this figure, the VPLWOA method is better than all other algorithms.
Besides, Fig. 13 depicts the average of PSNR and SSIM overall, the tested image at each threshold level. From this figure, it can be noticed the high ability of the proposed VLPWOA to find the optimal threshold value that improves the quality of the segmented image, and this reflected from the PSNR and SSIM values.
Based on the previous discussion, the proposed VPLWOA image segmentation outperforms the other methods. However, this approach has some limitations; for example, the time complexity needs to be improved, which can be decreased by enhancing the other phases of the VPL.
In addition, the parameters of the VPL algorithm need a suitable value to be determined. More efficient methods, such grid search, can be used to solve this problem. In the future, we can evaluate the proposed method over different applications and fields such as image retrieval and feature selection; moreover, we can develop it to work with the salient object detection (SOD) methods. SOD works to save the most visually distinctive items in an image [15, 17, 52], which can effectively improve the segmentation results, especially with the blood cell image segmentation.
Conclusions
This study introduces an alternative multilevel image segmentation method. The proposed method is called VPLWOA, given that it uses the operators of WOA to improve the learning phase of the traditional VPL algorithm. This phase has the main effect on the performance of the VPL. The proposed VPLWOA uses the histogram of the image as the input for maximizing the Otsu’s function to find the best threshold to segment the given image. The performance of the proposed VPLWOA is verified through a set of experiments using two datasets, and the results are compared with SSO, SCA, FA, VPL, and WOA. The experimental results show that the proposed VPLWOA outperforms the other algorithms in terms of PSNR, SSIM, and fitness function.
According to the promising results, the proposed method can be used in many other applications and subjects in future, such as feature selection and improving the clustering and classification of galaxy images. Also, the method can be applied in cloud computing and big data optimization.
Acknowledgments
This work is supported by the Hubei Provincinal Science and Technology Major Project of China under Grant No. 2020AEA011 and the Key Research & Developement Plan of Hubei Province of China under Grant No. 2020BAB100.
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants performed by any of the authors.
Informed consent
Informed was obtained from all individual participants included in the study.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Mohamed Abd Elaziz, Email: abd_el_aziz_m@yahoo.com.
Neggaz Nabil, Email: nabil.neggaz@univ-usto.dz.
Reza Moghdani, Email: reza.moghdani@gmail.com.
Ahmed A. Ewees, Email: ewees@du.edu.eg
Songfeng Lu, Email: lusongfeng@hust.edu.cn.
References
- 1.Ahmadi M, Kazemi K, Aarabi A, et al. Image segmentation using multilevel thresholding based on modified bird mating optimization. Multimed Tools Appl. 2019;78:23003–23027. doi: 10.1007/s11042-019-7515-6. [DOI] [Google Scholar]
- 2.Akay B. A study on particle swarm optimization and artificial bee colony algorithms for multilevel thresholding. Appl Soft Comput J. 2013;13:3066–3091. doi: 10.1016/j.asoc.2012.03.072. [DOI] [Google Scholar]
- 3.Awada W, Khoshgoftaar TM, Dittman D, et al (2012) A review of the stability of feature selection techniques for bioinformatics data. Proc 2012 IEEE 13th Int Conf Inf Reuse Integr IRI 2012 356–363. 10.1109/IRI.2012.6303031
- 4.Baby Resma KP, Nair MS (2018) Multilevel thresholding for image segmentation using Krill Herd Optimization algorithm. J King Saud Univ - Comput Inf Sci. 10.1016/j.jksuci.2018.04.007
- 5.Bao X, Jia H, Lang C. A novel hybrid Harris Hawks optimization for color image multilevel thresholding segmentation. IEEE Access. 2019;7:76529–76546. doi: 10.1109/ACCESS.2019.2921545. [DOI] [Google Scholar]
- 6.Bhandari AK, Singh N, Shubham S. An efficient optimal multilevel image thresholding with electromagnetism-like mechanism. Multimed Tools Appl. 2019;78:35733–35788. doi: 10.1007/s11042-019-08195-8. [DOI] [Google Scholar]
- 7.Bohat VK, Arya KV. A new heuristic for multilevel thresholding of images. Expert Syst Appl. 2019;117:176–203. doi: 10.1016/j.eswa.2018.08.045. [DOI] [Google Scholar]
- 8.Clerc M, Kennedy J (2002) The particle swarm — explosion , stability , and convergence in a multidimensional complex space. 6:58–73
- 9.El AMA, Ewees AA, Hassanien AE. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation. Expert Syst Appl. 2017;83:242–256. doi: 10.1016/j.eswa.2017.04.023. [DOI] [Google Scholar]
- 10.El AMA, Ewees AA, Hassanien AE. Multi-objective whale optimization algorithm for content-based image retrieval. Multimed Tools Appl. 2018;77:1–38. doi: 10.1007/s11042-018-5840-9. [DOI] [Google Scholar]
- 11.Elaziz MA, Oliva D, Ewees AA, Xiong S. Multi-level thresholding-based grey scale image segmentation using multi-objective multi-verse optimizer. Expert Syst Appl. 2019;125:112–129. doi: 10.1016/j.eswa.2019.01.047. [DOI] [Google Scholar]
- 12.Elaziz MA, Heidari AA, Fujita H, Moayedi H (2020) A competitive chain-based Harris Hawks Optimizer for global optimization and multi-level image thresholding problems. Appl Soft Comput:106347. 10.1016/j.asoc.2020.106347
- 13.Elaziz MA, Ewees AA, Yousri D, et al. An improved marine predators algorithm with fuzzy entropy for multi-level thresholding: real world example of COVID-19 CT image segmentation. IEEE Access. 2020;8:125306–125330. doi: 10.1109/ACCESS.2020.3007928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ewees AA, Abd Elaziz M, Al-Qaness MAA, et al. Improved artificial bee colony using sine-cosine algorithm for multi-level thresholding image segmentation. IEEE Access. 2020;8:26304–26315. doi: 10.1109/ACCESS.2020.2971249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fan D-P, Cheng M-M, Liu J-J, et al (2018) Salient objects in clutter: Bringing salient object detection to the foreground. In: Proceedings of the European conference on computer vision (ECCV). pp 186–202
- 16.Farshi TR (2018) A multilevel image thresholding using the animal migration optimization algorithm. Iran J Comput Sci:1–14
- 17.Fu K, Zhao Q, IY-H G, Yang J. Deepside: A general deep framework for salient object detection. Neurocomputing. 2019;356:69–82. doi: 10.1016/j.neucom.2019.04.062. [DOI] [Google Scholar]
- 18.Gao H, Fu Z, Pun CM, et al (2017) A multi-level thresholding image segmentation based on an improved artificial bee colony algorithm. Comput Electr Eng 0:1–8. 10.1016/j.compeleceng.2017.12.037
- 19.Gupta S, Deep K. Improved sine cosine algorithm with crossover scheme for global optimization. Knowledge-Based Syst. 2019;165:374–406. doi: 10.1016/j.knosys.2018.12.008. [DOI] [Google Scholar]
- 20.He L, Huang S. Modified firefly algorithm based multilevel thresholding for color image segmentation. Neurocomputing. 2017;240:152–174. doi: 10.1016/j.neucom.2017.02.040. [DOI] [Google Scholar]
- 21.Horng MH, Liou RJ. Multilevel minimum cross entropy threshold selection based on the firefly algorithm. Expert Syst Appl. 2011;38:14805–14811. doi: 10.1016/j.eswa.2011.05.069. [DOI] [Google Scholar]
- 22.Hussein WA, Sahran S, Sheikh Abdullah SNH. A new initialization algorithm for bees algorithm. Commun Comput Inf Sci. 2013;378 CCIS:39–52. doi: 10.1007/978-3-642-40567-9_4. [DOI] [Google Scholar]
- 23.Jia H, Peng X, Song W, et al. Multiverse optimization algorithm based on Lévy flight improvement for multithreshold color image segmentation. IEEE Access. 2019;7:32805–32844. doi: 10.1109/ACCESS.2019.2903345. [DOI] [Google Scholar]
- 24.Kapur JN, Sahoo PK, Wong AK. A new method for gray-level picture thresholding using the entropy of the histogram. Comput vision, Graph image Process. 1985;29:273–285. doi: 10.1016/0734-189X(85)90125-2. [DOI] [Google Scholar]
- 25.Khairuzzaman AKM, Chaudhury S. Multilevel thresholding using grey wolf optimizer for image segmentation. Expert Syst Appl. 2017;86:64–76. doi: 10.1016/j.eswa.2017.04.029. [DOI] [Google Scholar]
- 26.Kumar A, Konwer A, Kumar A, et al. Script identification in natural scene image and video frames using an attention based Convolutional-LSTM network. Pattern Recognit. 2019;85:172–184. doi: 10.1016/j.patcog.2018.07.034. [DOI] [Google Scholar]
- 27.Labati RD, Piuri V, Scotti F (2011) All-Idb: the acute lymphoblastic leukemia image database For image processing Ruggero Donida Labati IEEE Member, Vincenzo Piuri IEEE Fellow, Fabio Scotti IEEE Member Universit ` a degli Studi di Milano, Department of Information Technologies,. IEEE Int Conf Image Process 2045–2048
- 28.Liang J, Wang L (2018) A fast SAR image segmentation method based on improved chicken swarm optimization algorithm
- 29.Ma L, Liu X, Gao Y, et al. A new method of content based medical image retrieval and its applications to CT imaging sign retrieval. J Biomed Inform. 2017;66:148–158. doi: 10.1016/j.jbi.2017.01.002. [DOI] [PubMed] [Google Scholar]
- 30.Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- 31.Mittal H, Saraswat M. An optimum multi-level image thresholding segmentation using non-local means 2D histogram and exponential Kbest gravitational search algorithm. Eng Appl Artif Intell. 2018;71:226–235. doi: 10.1016/j.engappai.2018.03.001. [DOI] [Google Scholar]
- 32.Moghdani R, Salimifard K. Volleyball premier league algorithm. Appl Soft Comput J. 2018;64:161–185. doi: 10.1016/j.asoc.2017.11.043. [DOI] [Google Scholar]
- 33.Naji Alwerfali HS, A. A. Al-qaness, Abd Elaziz M, et al (2020) Multi-level image thresholding based on modified spherical search optimizer and fuzzy entropy. Entropy 22:328. 10.3390/e22030328 [DOI] [PMC free article] [PubMed]
- 34.Oliva D, Cuevas E, Pajares G, et al. A Multilevel thresholding algorithm using electromagnetism optimization. Neurocomputing. 2014;139:357–381. doi: 10.1016/j.neucom.2014.02.020. [DOI] [Google Scholar]
- 35.Oliva D, Hinojosa S, Elaziz MA, Ortega-Sánchez N (2018) Context based image segmentation using antlion optimization and sine cosine algorithm. Multimed Tools Appl:1–37. 10.1007/s11042-018-5815-x
- 36.Otsu N. A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern. 1979;9:62–66. doi: 10.1109/TSMC.1979.4310076. [DOI] [Google Scholar]
- 37.Ouadfel S, Taleb-Ahmed A. Social spiders optimization and flower pollination algorithm for multilevel image thresholding: A performance study. Expert Syst Appl. 2016;55:566–584. doi: 10.1016/j.eswa.2016.02.024. [DOI] [Google Scholar]
- 38.Park S, Hong K. Video semantic object segmentation by self-adaptation of DCNN. Pattern Recognit Lett. 2018;112:249–255. doi: 10.1016/j.patrec.2018.07.032. [DOI] [Google Scholar]
- 39.Reynolds AM, Smith AD, Reynolds DR, et al. Honeybees perform optimal scale-free searching flights when attempting to locate a food source. J Exp Biol. 2007;210:3763–3770. doi: 10.1242/jeb.009563. [DOI] [PubMed] [Google Scholar]
- 40.Rodríguez-Esparza E, Zanella-Calzada LA, Oliva D, et al. An efficient Harris hawks-inspired image segmentation method. Expert Syst Appl. 2020;155:113428. doi: 10.1016/j.eswa.2020.113428. [DOI] [Google Scholar]
- 41.Sarkar S, Das S, Chaudhuri SS. A multilevel color image thresholding scheme based on minimum cross entropy and differential evolution. Pattern Recognit Lett. 2015;54:27–35. doi: 10.1016/j.patrec.2014.11.009. [DOI] [Google Scholar]
- 42.Sharawi M, Zawbaa HM, Emary E, et al. Feature selection approach based on whale optimization algorithm. Ninth Int Conf Adv Comput Intell. 2017;2017:163–168. doi: 10.1109/ICACI.2017.7974502. [DOI] [Google Scholar]
- 43.Sun G, Zhang A, Yao Y, Wang Z. A novel hybrid algorithm of gravitational search algorithm with genetic algorithm for multi-level thresholding. Appl Soft Comput J. 2016;46:703–730. doi: 10.1016/j.asoc.2016.01.054. [DOI] [Google Scholar]
- 44.Tan Z, Zhang D (2020) A fuzzy adaptive gravitational search algorithm for two-dimensional multilevel thresholding image segmentation. J Ambient Intell Humaniz Comput. 10.1007/s12652-020-01777-7
- 45.Tang K, Yuan X, Sun T, et al. An improved scheme for minimum cross entropy threshold selection based on genetic algorithm. Knowledge-Based Syst. 2011;24:1131–1138. doi: 10.1016/j.knosys.2011.02.013. [DOI] [Google Scholar]
- 46.Touma HJ. Study of the economic dispatch problem on IEEE 30-bus system using whale optimization algorithm. Int J Eng Technol Sci. 2016;5:11–18. doi: 10.15282/ijets.5.2016.1.2.1041. [DOI] [Google Scholar]
- 47.Wang Y, Meng Q, Qi Q, et al. Region merging considering within- and between-segment heterogeneity: An improved hybrid remote-sensing image segmentation method. Remote Sens. 2018;10:1–26. doi: 10.3390/rs10050781. [DOI] [Google Scholar]
- 48.Wunnava A, Naik MK, Panda R, et al. A novel interdependence based multilevel thresholding technique using adaptive equilibrium optimizer. Eng Appl Artif Intell. 2020;94:103836. doi: 10.1016/j.engappai.2020.103836. [DOI] [Google Scholar]
- 49.Xing Z, Jia H. An improved thermal exchange optimization based GLCM for multi-level image segmentation. Multimed Tools Appl. 2020;79:12007–12040. doi: 10.1007/s11042-019-08566-1. [DOI] [Google Scholar]
- 50.Xing Z, Jia H. Modified thermal exchange optimization based multilevel thresholding for color image segmentation. Multimed Tools Appl. 2020;79:1137–1168. doi: 10.1007/s11042-019-08229-1. [DOI] [Google Scholar]
- 51.Xiong W, Xu J, Xiong Z, et al. Optik degraded historical document image binarization using local features and support vector machine ( SVM ) Opt - Int J Light Electron Opt. 2018;164:218–223. doi: 10.1016/j.ijleo.2018.02.072. [DOI] [Google Scholar]
- 52.Zhao J-X, Liu J-J, Fan D-P, et al. EGNet: Edge guidance network for salient object detection. In: Proceedings of the IEEE International Conference on Computer Vision; 2019. pp. 8779–8788. [Google Scholar]