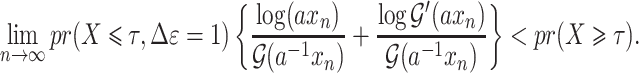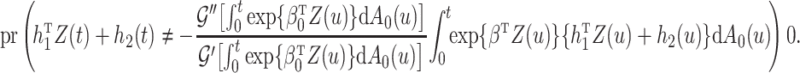Summary
Left-truncation poses extra challenges for the analysis of complex time-to-event data. We propose a general semiparametric regression model for left-truncated and right-censored competing risks data that is based on a novel weighted conditional likelihood function. Targeting the subdistribution hazard, our parameter estimates are directly interpretable with regard to the cumulative incidence function. We compare different weights from recent literature and develop a heuristic interpretation from a cure model perspective that is based on pseudo risk sets. Our approach accommodates external time-dependent covariate effects on the subdistribution hazard. We establish consistency and asymptotic normality of the estimators and propose a sandwich estimator of the variance. In comprehensive simulation studies we demonstrate solid performance of the proposed method. Comparing the sandwich estimator with the inverse Fisher information matrix, we observe a bias for the inverse Fisher information matrix and diminished coverage probabilities in settings with a higher percentage of left-truncation. To illustrate the practical utility of the proposed method, we study its application to a large HIV vaccine efficacy trial dataset.
Keywords: Cure model, Fine–Gray model, Proportional odds model, Pseudo risk set, Semiparametric transformation model, Time-varying covariate, Weighted conditional nonparametric maximum likelihood estimation
1. Introduction
Delayed entries arise in medical studies when individuals come under observation some time after the initial event. The time of the initial event is referred to as the left-truncation time or the delayed entry time, and we denote it by  . We consider a competing risks setting, in which individuals are exposed to several distinct event types, denoted by
. We consider a competing risks setting, in which individuals are exposed to several distinct event types, denoted by  , and only the first-occurring event is observable at time
, and only the first-occurring event is observable at time 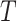 . Individuals are subject to independent right-censoring at
. Individuals are subject to independent right-censoring at 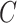 . Defining
. Defining 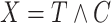 and
and 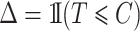 , we observe
, we observe 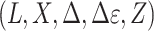 only for those individuals with
only for those individuals with 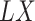 . Such a setting is referred to as a competing risks setting with left-truncated and right-censored data. Individuals with
. Such a setting is referred to as a competing risks setting with left-truncated and right-censored data. Individuals with  are subject to left-truncation. We will make the common assumption that
are subject to left-truncation. We will make the common assumption that  and
and  are independent given a vector of covariates
are independent given a vector of covariates 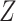 .
.
With a sample that represents only those individuals whose event and censoring times exceed the left-truncation time, it is well known that delayed entries need to be taken into account when fitting survival regression models. For the analysis of survival data with independent left-truncation and right-censoring and, without competing risks, a conditional likelihood approach was proposed by Andersen et al. (1988, 2013), Keiding & Gill (1990) and Owen (2001), among others. In particular, one can estimate the regression parameters in proportional hazards models using a conditional partial likelihood, where individuals are included in the risk set from their time of entrance until an event of interest or a censoring is observed.
A common approach used in competing risks settings with independent right-censoring is to model the cause-specific hazard 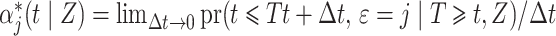 , which can be interpreted as the instantaneous risk of dying from cause
, which can be interpreted as the instantaneous risk of dying from cause 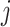 at time
at time 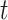 conditional on being alive at
conditional on being alive at 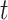 . The cumulative incidence function, defined as
. The cumulative incidence function, defined as 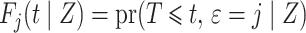
 is a complex function of all cause-specific hazards. Therefore, estimated parameters targeting the cause-specific hazard cannot be interpreted with regard to the corresponding cumulative incidence function. An alternative approach models the subdistribution hazard for the event of interest,
is a complex function of all cause-specific hazards. Therefore, estimated parameters targeting the cause-specific hazard cannot be interpreted with regard to the corresponding cumulative incidence function. An alternative approach models the subdistribution hazard for the event of interest,
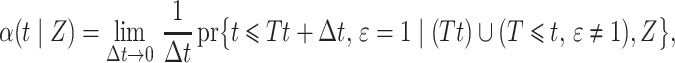 |
as defined by Gray (1988), which is the instantaneous risk of experiencing an event of interest at time 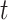 conditional on not having experienced an event of interest until
conditional on not having experienced an event of interest until 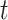 . The subdistribution hazard is directly related to the corresponding cumulative incidence function through
. The subdistribution hazard is directly related to the corresponding cumulative incidence function through 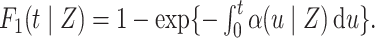 Regression parameters targeting the subdistribution hazard are thus directly interpretable with regard to the cumulative incidence function. The subdistribution hazard is also linked to a cure model formulation of the competing risks setting (Bellach et al., 2019) and may be interpreted as the hazard of the event time
Regression parameters targeting the subdistribution hazard are thus directly interpretable with regard to the cumulative incidence function. The subdistribution hazard is also linked to a cure model formulation of the competing risks setting (Bellach et al., 2019) and may be interpreted as the hazard of the event time 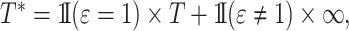 as in Fine & Gray (1999).
as in Fine & Gray (1999).
Regression modelling for the subdistribution of a competing risk with independent left-truncation and right-censoring has so far been investigated only for the proportional hazards model (Geskus, 2011; Zhang et al., 2011). As the proportional hazards assumption is not valid in general, it is of interest to consider a more general direct regression model. Moreover, the existing literature does not provide intuition for the proposed weights, and in particular the weighted risk set appears to be unexplained. The purpose of this paper is to give comprehensible arguments for the proposed weights and risk sets, and to derive estimators for a general direct regression model targeting the subdistribution hazard based on a conditional nonparametric maximum likelihood procedure.
We first investigate a competing risks model in which the competing risk event is associated with a cure event. This is frequently the case with infectious diseases. As a historic example, Edward Jenner’s observation that prior infection with cowpox confers protective immunity against smallpox played a pivotal role in the development of the smallpox vaccine, which led to the eradication of smallpox in 1980. A more recent example is vaccination against the dengue virus; epidemiological data support the idea that disease caused by a given dengue genotype prevents disease due to other dengue genotypes within the same serotype (Juraska et al., 2018).
In the cure model setting, left-truncation and right-censoring times can be observed independently of the cure event. Cured individuals with  and
and 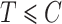 are incorporated into the risk set, which is denoted by
are incorporated into the risk set, which is denoted by 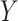 . It is always possible to determine the size of such a risk set from the observed data, although the size of the cure fraction may be unknown. For the competing risks model, individuals with a previous competing risk event are incorporated into the risk set like a cure fraction, as they are no longer exposed to the event of interest. It should be noticed that the terms risk process and risk set are rooted in the tradition of survival analysis and should not be understood in a literal sense. The risk set in a subdistribution hazard model consists of those individuals who have not experienced an event of interest up to time
. It is always possible to determine the size of such a risk set from the observed data, although the size of the cure fraction may be unknown. For the competing risks model, individuals with a previous competing risk event are incorporated into the risk set like a cure fraction, as they are no longer exposed to the event of interest. It should be noticed that the terms risk process and risk set are rooted in the tradition of survival analysis and should not be understood in a literal sense. The risk set in a subdistribution hazard model consists of those individuals who have not experienced an event of interest up to time 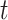 , and may never experience an event of interest because of a cure event or competing risk event prior to
, and may never experience an event of interest because of a cure event or competing risk event prior to 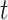 . In particular, not all individuals in the risk set are actually at risk for the event of interest.
. In particular, not all individuals in the risk set are actually at risk for the event of interest.
First, we derive the conditional likelihood function for the cure model, adhering to the principle that the true parameter can be estimated efficiently by the value that maximizes the probability of the observed data. Second, we study the classical competing risks setting, where the occurrence of any event would terminate observation. We use the cure model to obtain new insights into the direct competing risks regression model with left-truncated and right-censored data. For estimation, we weight using the observed data, mimicking the structure that would have occurred in the cure model setting, and define the pseudo risk set. Specifically, the expected number of individuals in the pseudo risk set is by construction equal to the expected number of individuals in the corresponding cure model risk set.
We derived the proposed weighted conditional nonparametric maximum likelihood estimators using the R (R Development Core Team, 2020) function optim with the method specified as BFGS, which utilizes the Broyden–Fletcher–Goldfarb–Shanno algorithm, a quasi-Newton method. For all simulation studies and clinical trial data that we investigated, the optimization worked very reliably.
2. Pseudo risk set and weighted likelihood function
2.1. Cure model with complete data
We start by investigating a competing risks model in which the competing risk event is connected to the cure of the subject. Denoting an event of interest by 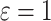 and the competing event by
and the competing event by  , the cure event at
, the cure event at 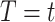 implies that
implies that 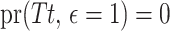 , although the subject is still observable. Let
, although the subject is still observable. Let  denote the duration of the study, with administrative censoring at
denote the duration of the study, with administrative censoring at 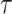 . For settings with only administrative censoring at
. For settings with only administrative censoring at  , we have
, we have 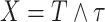 and
and 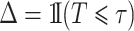 . For a random sample
. For a random sample  , the observed data are
, the observed data are 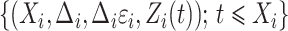 for
for 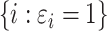 and
and 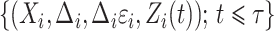 for
for  . The process counting the events of interest is
. The process counting the events of interest is 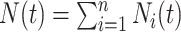 where
where 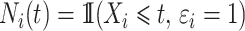 . The individual at-risk process is
. The individual at-risk process is 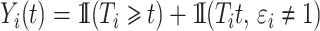
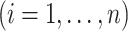 , and
, and 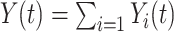 is the cardinality of the risk set
is the cardinality of the risk set 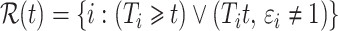 for
for 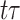 .
.
We denote the cumulative subdistribution hazard for the event of interest by 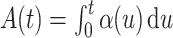 and define
and define 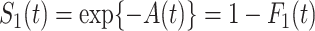 . As argued in Bellach et al. (2019),
. As argued in Bellach et al. (2019), 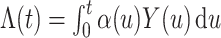 is the compensator of
is the compensator of 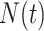 with respect to the filtration
with respect to the filtration 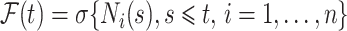 , and the Nelson–Aalen estimator for the cumulative subdistribution hazard can be derived from the Doob decomposition
, and the Nelson–Aalen estimator for the cumulative subdistribution hazard can be derived from the Doob decomposition  , with
, with 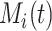 denoting the martingale. A likelihood function as in Bellach et al. (2019, § 2.1) can be derived by considering that the contribution for an event of interest is
denoting the martingale. A likelihood function as in Bellach et al. (2019, § 2.1) can be derived by considering that the contribution for an event of interest is 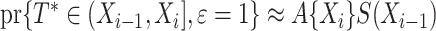 with
with 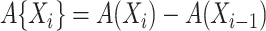 , and the contribution for a cure event or administrative censoring at
, and the contribution for a cure event or administrative censoring at 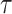 is
is 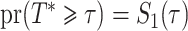 . The estimator for the cumulative subdistribution hazard that is obtained from maximizing this likelihood function is equivalent to the Nelson–Aalen estimator.
. The estimator for the cumulative subdistribution hazard that is obtained from maximizing this likelihood function is equivalent to the Nelson–Aalen estimator.
2.2. Cure model with independent left-truncation and right-censoring
With independent left-truncation and right-censoring, we have 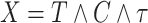 and
and 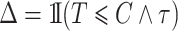 . The observed data are
. The observed data are  for subjects
for subjects 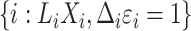 ,
, 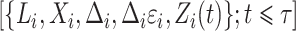 for subjects
for subjects 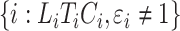 and
and 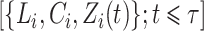 for subjects
for subjects 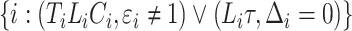 . The process counting the observed events of interest is denoted by
. The process counting the observed events of interest is denoted by 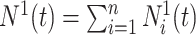 with
with  , and
, and 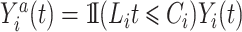 is the individual at-risk process for subject
is the individual at-risk process for subject 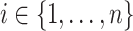 . Then
. Then 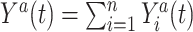 is the cardinality of the risk set
is the cardinality of the risk set
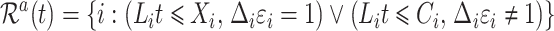 |
(1) |
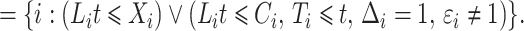 |
(2) |
The risk set in (1) is based on observable data. Subjects enter the study at 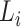 independently of a possible cure event and remain in the risk set until an event of interest is observed at
independently of a possible cure event and remain in the risk set until an event of interest is observed at 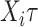 or until censoring at
or until censoring at 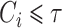 . The size of the cure fraction
. The size of the cure fraction 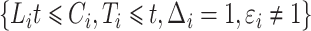 may be unobservable for the theoretical decomposition (2), with subjects entering the study after the cure event. For modelling of the subdistribution hazard, however, only knowledge about the size of the risk sets
may be unobservable for the theoretical decomposition (2), with subjects entering the study after the cure event. For modelling of the subdistribution hazard, however, only knowledge about the size of the risk sets 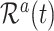 is required, which can be obtained from (1) regardless of the specific decomposition (2).
is required, which can be obtained from (1) regardless of the specific decomposition (2).
A Nelson–Aalen estimator for the cumulative subdistribution hazard can be derived from the weighted Doob decomposition 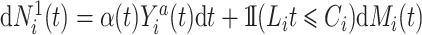 . The same estimate may also be derived from a weighted conditional likelihood function obtained by considering that the contribution for an observed event of interest at
. The same estimate may also be derived from a weighted conditional likelihood function obtained by considering that the contribution for an observed event of interest at 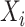 is
is 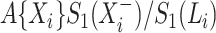 with
with 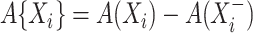 , the contribution for an observed censoring is
, the contribution for an observed censoring is 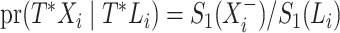 , and the contribution for a cured individual with
, and the contribution for a cured individual with 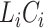 is
is 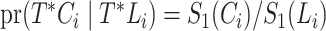 , regardless of whether the cure event occurred before or after the entrance time
, regardless of whether the cure event occurred before or after the entrance time 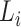 . We thus obtain the conditional likelihood function
. We thus obtain the conditional likelihood function
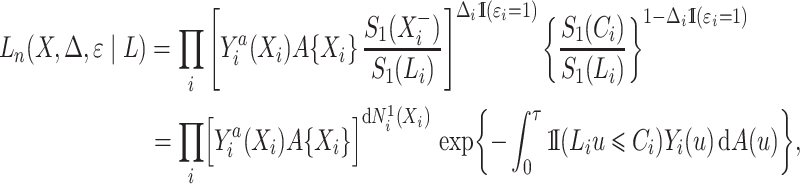 |
where the cumulative baseline subdistribution hazard is approximated by a step function 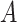 with jumps at the observed event times, which are denoted by
with jumps at the observed event times, which are denoted by 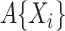 .
.
2.3. Left-truncated and right-censored competing risks data
Modelling the subdistribution hazard for the competing risks model requires a reconstruction of the cure model risk set, where the cure fraction consists of 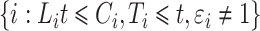 . For the competing risks model, however, only subjects with
. For the competing risks model, however, only subjects with 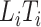 are observable, and in particular subjects
are observable, and in particular subjects 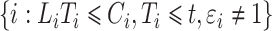 are assigned to the cure fraction. The observed data are
are assigned to the cure fraction. The observed data are 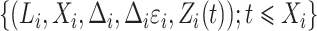 for subjects
for subjects 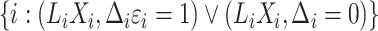 and
and 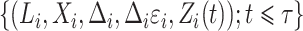 for subjects
for subjects 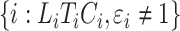 .
.
To maintain the cure model structure, an adjustment for hypothetical left-truncation after competing risk events and right-censoring of individuals in the cure fraction is required. We apply inverse probability of censoring weighting. A weight function  that consistently estimates
that consistently estimates 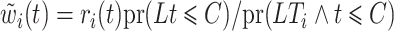 , where
, where 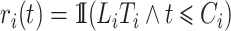 , would be justified by
, would be justified by 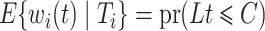 . We make the decomposition
. We make the decomposition 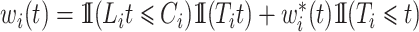 , with simplified weights
, with simplified weights 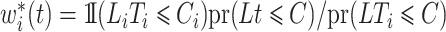 , to define the pseudo risk set
, to define the pseudo risk set
 |
The process counting the observable events of interest is defined by 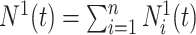 , with
, with  . A Nelson–Aalen-type estimator for the cumulative subdistribution hazard is obtained from the weighted Doob decomposition
. A Nelson–Aalen-type estimator for the cumulative subdistribution hazard is obtained from the weighted Doob decomposition 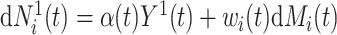 , and may also be derived from the weighted conditional likelihood function from § 2.2, where the risk set indicator
, and may also be derived from the weighted conditional likelihood function from § 2.2, where the risk set indicator 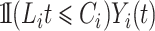 is replaced by
is replaced by  :
:
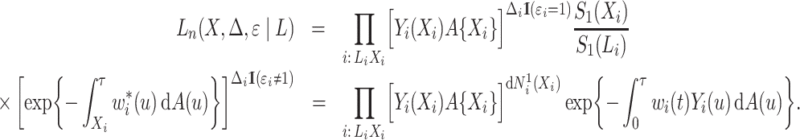 |
A product limit estimator for the cumulative incidence function can be derived based on the Nelson–Aalen-type estimator for the subdistribution hazard. Zhang et al. (2009) and Geskus (2011) proved its equivalence to the fully efficient Aalen–Johansen estimator. This suggests that the weighted conditional likelihood function is a promising candidate for likelihood-based inference on the subdistribution hazard.
3. Definition and estimation of the weights
We use the following representation of the theoretical weights:
 |
Denoting the number of observable events by 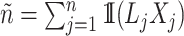 and the number of observable individuals by
and the number of observable individuals by 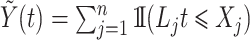 , we estimate
, we estimate 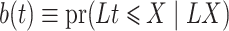 consistently by
consistently by 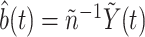 . The unconditional probabilities
. The unconditional probabilities 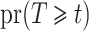 and
and 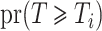 can be estimated with the product limit estimator. Let
can be estimated with the product limit estimator. Let 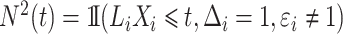 be the process counting the competing risk events. We obtain the estimated weights
be the process counting the competing risk events. We obtain the estimated weights
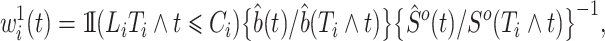 |
where 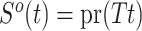 is the left-truncated version of the product limit estimator for the overall survival, as proposed by Zhang et al. (2011). Decomposing the weight yields
is the left-truncated version of the product limit estimator for the overall survival, as proposed by Zhang et al. (2011). Decomposing the weight yields 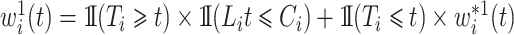 , with
, with
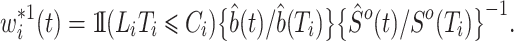 |
Geskus (2011) introduced weights based on the product limit estimator 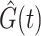 estimating
estimating 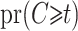 and the inverse product limit estimator of the delayed entries
and the inverse product limit estimator of the delayed entries 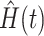 estimating
estimating 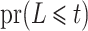 , which had previously been investigated by Keiding & Gill (1990) for a model with independent left-truncation and no censoring. A common assumption for left-truncated and right-censored data is independence of
, which had previously been investigated by Keiding & Gill (1990) for a model with independent left-truncation and no censoring. A common assumption for left-truncated and right-censored data is independence of  and
and 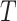 , but not independence of
, but not independence of 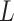 and
and  . For this reason, the validity of the weights
. For this reason, the validity of the weights
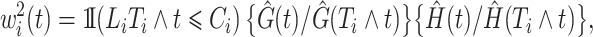 |
which may be decomposed as 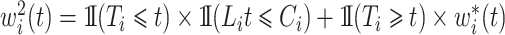 with
with
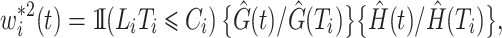 |
is not immediately apparent. A theoretical justification using results of He & Yang (1998) would require independence of 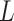 and
and  . Interestingly, the weights
. Interestingly, the weights 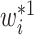 and
and 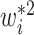 are equivalent with continuous
are equivalent with continuous 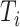 , as we prove in the Supplementary Material, thereby justifying the weights proposed by Geskus (2011).
, as we prove in the Supplementary Material, thereby justifying the weights proposed by Geskus (2011).
For a competing risks model with only left-truncation and no right-censoring, the weights simplify; for example, the theoretical weights in this case are 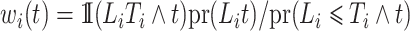 .
.
4. General regression model
We consider estimation of a general model for the cumulative subdistribution hazard
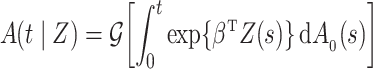 |
as in Bellach et al. (2019), akin to a general semiparametric regression model for survival and recurrent event data without left-truncation and competing risks, which has been investigated by Zeng&Lin (2006); here 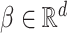 is a vector of unknown regression parameters,
is a vector of unknown regression parameters, 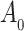 is an unspecified increasing function, and
is an unspecified increasing function, and 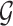 is a thrice continuously differentiable and strictly increasing function with
is a thrice continuously differentiable and strictly increasing function with  ,
, 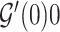 and
and 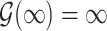 . Regularity conditions for this model, which are considerably weaker than those in Zeng & Lin (2006), are specified in the Appendix. Special cases of the general model include the Box–Cox transformation models with link function
. Regularity conditions for this model, which are considerably weaker than those in Zeng & Lin (2006), are specified in the Appendix. Special cases of the general model include the Box–Cox transformation models with link function 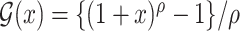 for
for 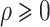 , and the logarithmic transformation models with link function
, and the logarithmic transformation models with link function 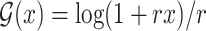 for
for 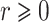 (Chen et al., 2002). The Fine–Gray model under left-truncation and right-censoring (Geskus, 2011; Zhang et al., 2011) is also a special case. In particular, the proportional hazards model is the Box–Cox transformation model with
(Chen et al., 2002). The Fine–Gray model under left-truncation and right-censoring (Geskus, 2011; Zhang et al., 2011) is also a special case. In particular, the proportional hazards model is the Box–Cox transformation model with 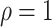 and the limiting logarithmic transformation model with
and the limiting logarithmic transformation model with 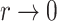 , while the proportional odds model is the logarithmic transformation model with
, while the proportional odds model is the logarithmic transformation model with 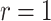 and the limiting Box–Cox transformation model with
and the limiting Box–Cox transformation model with 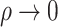 . If
. If 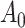 is differentiable, the instantaneous subdistribution hazard rate is defined by
is differentiable, the instantaneous subdistribution hazard rate is defined by
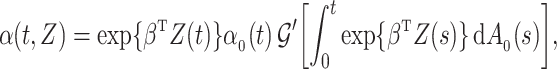 |
(3) |
where 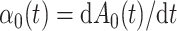 denotes the baseline subdistribution hazard and
denotes the baseline subdistribution hazard and  is a vector of external time-dependent or time-independent covariates.
is a vector of external time-dependent or time-independent covariates.
For the cure model with independent left-truncation and right-censoring, we define 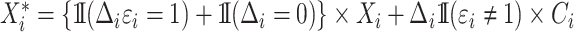 to obtain the conditional loglikelihood
to obtain the conditional loglikelihood
 |
By rearranging terms in the second sum, this can be written as
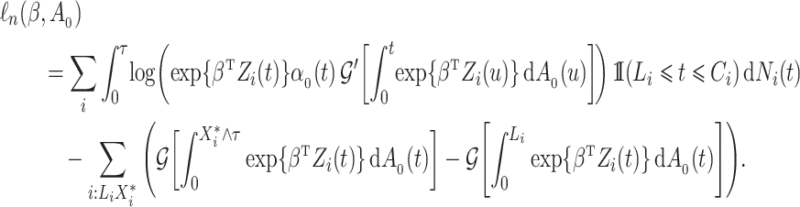 |
With independently left-truncated and right-censored competing risks data, we obtain
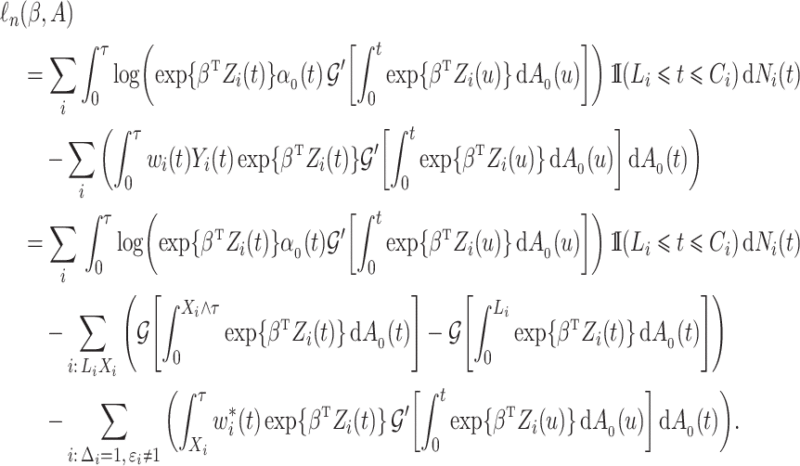 |
(4) |
For statistical inference, the baseline subdistribution hazard  is approximated by a sequence of step functions, and the weighted nonparametric maximum likelihood estimator
is approximated by a sequence of step functions, and the weighted nonparametric maximum likelihood estimator 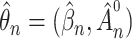 is obtained by maximizing the discretized loglikelihood function with respect to
is obtained by maximizing the discretized loglikelihood function with respect to 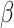 and the jump sizes
and the jump sizes 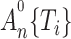 . In the Appendix and Supplementary Material we prove the following theorem.
. In the Appendix and Supplementary Material we prove the following theorem.
Theorem 1.
The weighted nonparametric maximum likelihood estimator
is uniformly consistent.
With an application of Lemma S2 from the Supplementary Material, which is based on Theorem 3.3.1 in van der Vaart & Wellner (1996), we derive the following theorem.
Theorem 2.
We have that
converges weakly to a zero-mean Gaussian process.
We prove these theorems first for the cure model set-up, thereby adapting arguments by Murphy (1994, 1995), Parner (1998), Zeng & Lin (2006) and Bellach et al. (2019). These results are then adapted to the direct competing risks regression model, which has a similar mathematical structure.
To obtain weak convergence and for variance estimation, we consider the linear functionals
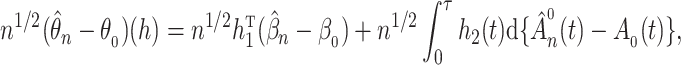 |
where 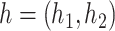 , with
, with 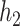 being a function in the Skorohod space
being a function in the Skorohod space 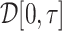 and
and 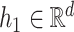 . Let
. Let 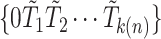 be the ordered times for the event of interest and let
be the ordered times for the event of interest and let 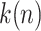 be the number of such events. Defining a vector
be the number of such events. Defining a vector 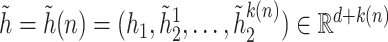 with
with 
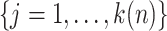 , the asymptotic variance of the linear functional can be estimated by the sandwich estimator
, the asymptotic variance of the linear functional can be estimated by the sandwich estimator
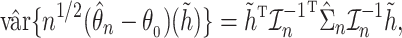 |
where 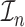 is the observed Fisher information matrix with respect to
is the observed Fisher information matrix with respect to 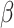 and the jump sizes, and
and the jump sizes, and  is the estimated variance of the score with respect to
is the estimated variance of the score with respect to 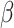 and the jump sizes, with
and the jump sizes, with 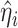 ,
, 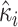 and
and 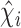 denoting the components of the independent and identically distributed decomposition given in the Supplementary Material. Analogously, we obtain the estimator for the covariances of
denoting the components of the independent and identically distributed decomposition given in the Supplementary Material. Analogously, we obtain the estimator for the covariances of 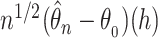 and
and 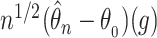 , with
, with  and with corresponding vectors
and with corresponding vectors 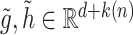 :
:
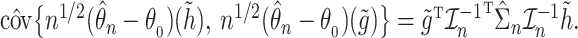 |
For the cure model, the sandwich estimator simplifies to the inverse Fisher information. However, for the competing risks model with independent left-truncation and right-censoring, the middle term 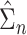 contains additional terms reflecting the extra variability from the estimated weights.
contains additional terms reflecting the extra variability from the estimated weights.
5. Simulation studies
We conducted simulation studies for the Fine–Gray model and for the proportional odds model to evaluate the bias, the empirical and model-based variances, and the coverage probabilities of the proposed method for different sample sizes. We considered settings with two different event types. All simulation results are based on 1000 repetitions.
For our first set of simulations with fixed covariates, displayed in Table 1, we used the model formulations in Fine & Gray (1999) and Fine (2001), which are specified in the Supplementary Material. The covariates  and
and 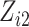
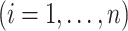 were generated independently from a standard normal distribution. For the second set of simulations, displayed in Table 2, we developed a new method to generate event times for competing risks models with binary time-dependent covariates, the details of which are given in the Supplementary Material. We generated
were generated independently from a standard normal distribution. For the second set of simulations, displayed in Table 2, we developed a new method to generate event times for competing risks models with binary time-dependent covariates, the details of which are given in the Supplementary Material. We generated  from a standard normal distribution and generated
from a standard normal distribution and generated 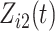 as a time-dependent covariate with one transition from 0 to 1, thereby assuming that the covariate process is observable after the competing risk event. The transition time for
as a time-dependent covariate with one transition from 0 to 1, thereby assuming that the covariate process is observable after the competing risk event. The transition time for 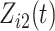 was generated from a standard exponential distribution.
was generated from a standard exponential distribution.
Table 1.
Simulation results for the Fine–Gray and proportional odds models. For columns 3–8, 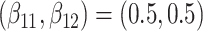 ,
, 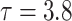 ,
, 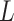 is generated from
is generated from 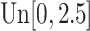 with probability
with probability 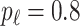 and set to zero otherwise, and
and set to zero otherwise, and  with
with 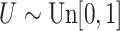 ; approximately
; approximately 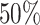 are left-truncated,
are left-truncated, 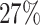 are censored,
are censored, 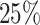 are events of interest and
are events of interest and 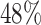 are competing events. For columns 9–14,
are competing events. For columns 9–14, 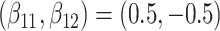 ,
,  ,
, 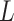 is generated from
is generated from  with probability
with probability 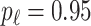 and set to
and set to 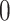 otherwise, and
otherwise, and  with
with 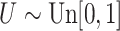 ; approximately
; approximately 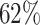 are left-truncated,
are left-truncated, 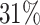 are censored,
are censored, 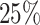 are events of interest and
are events of interest and  are competing events
are competing events
Fine–Gray model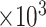
|
Proportional odds model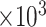
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size | Parameter | Bias | SE |
|

|
CP
|
CP
|
Bias | SE |
|
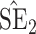
|
CP
|
CP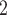
|
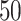
|
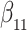
|
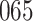
|
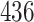
|
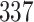
|

|
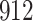
|
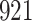
|
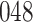
|
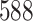
|

|

|

|
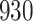
|
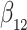
|
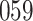
|
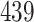
|

|
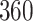
|
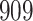
|

|
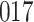
|

|
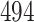
|

|
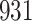
|
|
|
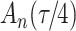
|
|
|
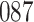
|
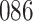
|
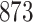
|
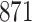
|
|

|

|
|
|
|
|
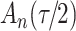
|
|
|
|
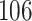
|
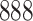
|

|
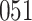
|

|
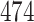
|
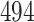
|
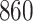
|
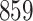
|
|
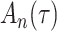
|
|
|

|
|
|
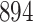
|
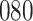
|
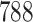
|
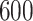
|
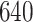
|
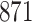
|
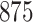
|
|
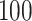
|
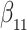
|

|
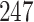
|
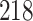
|
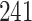
|
|
|

|
|
|
|
|
|
|
|
|
|

|

|
|
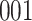
|
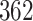
|
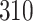
|
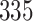
|
|
|
|
|

|
|
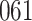
|

|
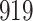
|
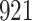
|

|
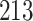
|
|
|
|
|
|
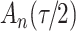
|
|
|
|
|
|
|

|
|
|
|
|
|
|
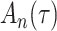
|

|
|
|
|
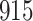
|
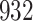
|

|

|
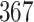
|
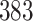
|
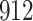
|
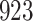
|
|
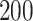
|
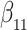
|
|

|
|
|
|
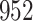
|
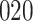
|
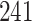
|
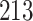
|
|
|
|

|
|

|

|
|
|
|
|
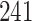
|
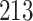
|
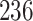
|
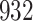
|
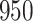
|
|
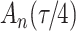
|

|
|
|

|
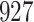
|
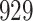
|
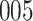
|

|
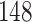
|
|
|
|
|
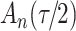
|
|
|
|
|
|
|
|
|
|

|
|

|
|
|
|
|
|

|
|
|
|
|

|
|
|
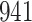
|
|

|
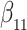
|

|
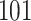
|
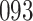
|
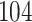
|
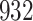
|
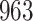
|
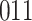
|
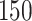
|
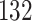
|
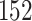
|
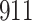
|

|

|
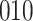
|
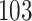
|
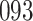
|
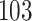
|
|
|
|
|
|
|
|
|
|

|

|
|
|

|
|
|
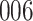
|
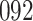
|
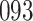
|
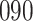
|
|
|
|
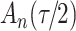
|
|
|
|
|

|
|
|
|
|
|
|
|
|

|
|

|
|
|
|
|
|
|

|
|
|
|
|
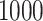
|
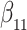
|

|
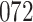
|
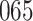
|
|
|
|
|
|
|
|
|
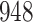
|
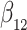
|
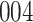
|
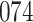
|

|
|

|
|
|
|
|

|
|
|
|
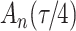
|
|
|
|

|
|

|
|
|
|

|
|
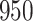
|
|
|
|
|
|
|
|
|
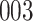
|
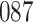
|

|
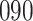
|
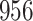
|
|
|
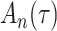
|

|
|
|
|
|

|
|
|
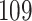
|
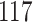
|

|
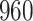
|
|
Bias, absolute value of bias; SE, empirical standard error;  , inverse Fisher information;
, inverse Fisher information; 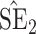 , sandwich estimator; CP
, sandwich estimator; CP and CP
and CP , coverage probabilities of
, coverage probabilities of  confidence intervals for
confidence intervals for 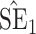 and
and 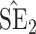 , respectively; all results are multiplied by
, respectively; all results are multiplied by 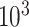 .
.
Table 2.
Results of simulation studies with external time-dependent covariates. For columns 3–8, 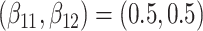 ,
, 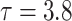 ,
,  is generated from
is generated from 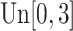 with probability
with probability 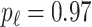 and set to
and set to  otherwise, and
otherwise, and 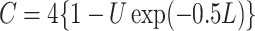 with
with 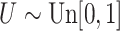 ; approximately
; approximately 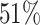 are left-truncated,
are left-truncated, 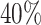 are censored,
are censored, 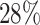 are events of interest and
are events of interest and 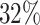 are competing events. For columns 9–14,
are competing events. For columns 9–14, 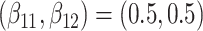 ,
,  ,
, 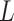 is generated from
is generated from 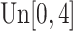 with probability
with probability 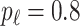 and set to
and set to 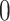 otherwise, and
otherwise, and 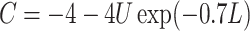 with
with 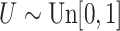 ; approximately
; approximately 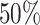 are left-truncated,
are left-truncated, 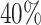 are censored,
are censored, 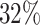 are events of interest and
are events of interest and 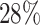 are competing events
are competing events
Fine–Gray model
|
Proportional odds model
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size | Parameter | Bias | SE |
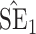
|
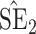
|
CP
|
CP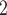
|
Bias | SE |
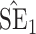
|
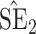
|
CP
|
CP
|
|
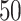
|
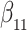
|
|

|
|
|
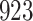
|
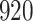
|
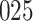
|

|
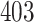
|
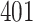
|
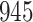
|

|
|
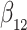
|
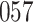
|
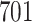
|
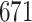
|
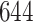
|
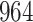
|
|
|

|
|
|
|
|
||
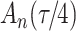
|
|

|
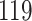
|
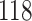
|
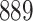
|

|
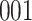
|
|
|
|
|
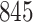
|
||

|
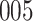
|
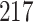
|
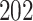
|
|
|
|
|
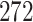
|

|
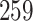
|
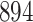
|
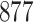
|
||
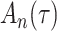
|
|
|
|
|
|
|
|

|
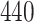
|
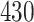
|
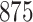
|
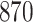
|
||
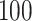
|
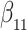
|
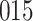
|

|
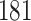
|
|
|
|

|
|
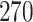
|
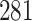
|
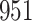
|
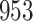
|
|
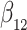
|
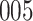
|
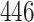
|
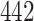
|
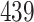
|
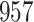
|
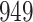
|

|
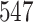
|
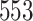
|
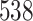
|
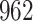
|
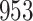
|
||
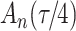
|
|
|
|
|
|
|
|
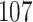
|
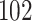
|

|
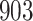
|
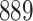
|
||
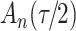
|
|
|
|
|
|
|
|
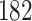
|

|
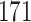
|

|
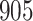
|
||
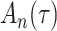
|
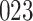
|
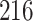
|

|
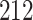
|
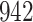
|
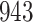
|
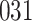
|

|
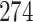
|
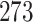
|
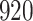
|
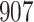
|
||

|
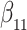
|
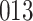
|
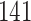
|
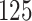
|
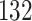
|
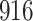
|
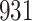
|
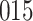
|
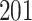
|
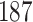
|
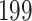
|
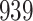
|

|
|

|

|
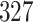
|
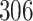
|
|
|
|
|

|
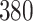
|
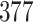
|
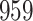
|
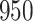
|
||
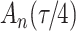
|
|
|
|

|
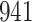
|
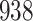
|
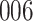
|
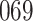
|
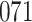
|

|

|
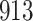
|
||
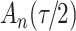
|
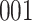
|

|
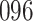
|

|
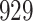
|
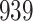
|
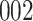
|

|
|
|
|
|
||
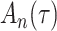
|
|
|
|

|
|
|
|

|
|
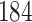
|
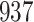
|
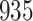
|
||
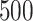
|
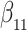
|

|
|
|
|
|
|
|
|
|

|
|
|
|

|
|
|
|
|
|

|
|
|

|
|
|
|
||
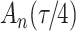
|
|
|
|
|
|
|
|
|
|

|
|

|
||
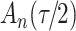
|

|
|
|
|

|
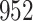
|
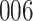
|
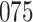
|

|
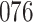
|
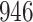
|
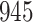
|
||
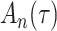
|
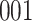
|
|
|

|

|
|

|
|
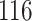
|
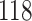
|
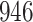
|
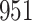
|
||
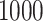
|
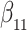
|
|
|
|
|
|
|
|
|
|
|

|
|
|
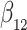
|
|
|
|
|
|

|
|
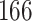
|

|
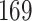
|
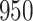
|
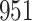
|
||

|
|
|
|
|

|
|
|
|
|
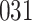
|
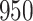
|
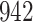
|
||
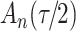
|

|
|
|
|
|

|
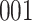
|
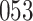
|
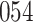
|
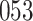
|
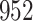
|
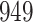
|
||

|
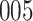
|
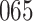
|
|
|
|
|

|

|
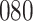
|
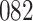
|
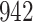
|

|
||
Bias, absolute value of bias; SE, empirical standard error; 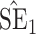 , inverse Fisher information;
, inverse Fisher information; 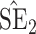 , sandwich estimator; CP
, sandwich estimator; CP and CP
and CP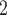 , coverage probabilities of
, coverage probabilities of 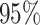 confidence intervals for
confidence intervals for 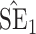 and
and 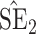 , respectively; all results are multiplied by
, respectively; all results are multiplied by 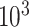 .
.
In all simulation studies the performance of the weighted nonparametric maximum likelihood estimator is solid, even for small sample sizes, in terms of the bias, and the standard errors and coverage probabilities of the proposed sandwich estimator. The bias is generally small, the standard errors decrease at rate 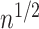 , the proposed sandwich estimators are close to the empirical variance estimators, and the coverage probabilities are close to the nominal level of
, the proposed sandwich estimators are close to the empirical variance estimators, and the coverage probabilities are close to the nominal level of 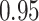 , particularly for sample sizes
, particularly for sample sizes 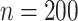 ,
, 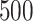 and
and 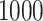 .
.
Comparing the results for the estimated variances, in particular for the additional simulation studies presented in the Supplementary Material, it is observed that the proposed sandwich estimator has the desired properties, while the inverse Fisher information matrix underestimates the variance of the parameter estimates, and, moreover, the coverage probabilities are clearly smaller than the desired value of 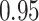 .
.
Simulation results reported in the Supplementary Material confirm our theoretical results on the equivalence of the weights proposed by Geskus (2011) and Zhang et al. (2011).
6. Application to HIV vaccine efficacy trial data
We analysed data from the HVTN 503 preventive HIV vaccine efficacy trial in South Africa, to assess how participant factors are associated with the time from reaching adulthood to diagnosis of genotype-specific HIV-1 infection. These data, from 784 individuals screened at age 18 and above, are left-truncated because only those who test negative for HIV-1 are eligible to enrol in the trial. It was of particular interest to investigate the efficacy of the vaccine and the effects of sex at birth, and body mass index at enrolment on the time to infection with the HIV-1 169K virus, which has a vaccine-matched residue at position 169 of the V2 loop, compared with the effects on the time to infection with the HIV-1 K169! virus, which has a vaccine-mismatched residue at position 169. This question is relevant because an HIV vaccine is currently undergoing testing for efficacy in the HVTN 702 randomized, placebo-controlled trial in South Africa, and it is hypothesized that the efficacy of this vaccine against the virus type HIV-1 169K is superior to that against type HIV-1 K169!, because a previous trial of a similar HIV vaccine showed greater efficacy against HIV-1 type 169K (Rolland et al., 2012).
A total of 28 infections with HIV-1 virus type 169K and 15 infections with HIV-1 virus type K169! were observed. We conducted backward selection starting with the covariates assignment to vaccine, sex at birth and body mass index, and then removed the last, which was clearly nonsignificant.
Our findings, displayed in Tables 3 and 4, indicate that women in South Africa tend to be infected at earlier ages than men. For HIV-1 type 169K, the results can be interpreted as an  increase in the expected subdistribution hazard for women, with
increase in the expected subdistribution hazard for women, with 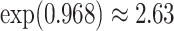 , and an
, and an 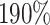 increase in the expected odds ratio, with
increase in the expected odds ratio, with 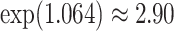 . For HIV-1 type K169! this would be interpreted as a
. For HIV-1 type K169! this would be interpreted as a  increase in the expected subdistribution hazard for women, with
increase in the expected subdistribution hazard for women, with 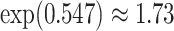 , and a
, and a 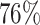 increase in the expected odds ratio, with
increase in the expected odds ratio, with  . As illustrated in Fig. 1, for infection with HIV-1 type 169K, the fit of the model may be improved with a logarithmic transformation and parameter
. As illustrated in Fig. 1, for infection with HIV-1 type 169K, the fit of the model may be improved with a logarithmic transformation and parameter  , while for infection with HIV-1 type K169! a Box–Cox transformation with a larger parameter
, while for infection with HIV-1 type K169! a Box–Cox transformation with a larger parameter 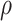 may yield a moderately improved fit over the Fine–Gray and proportional odds models. The observed direct association with risk of being female in comparison to being male was therefore significantly greater for HIV-1 type 169K than for HIV-1 type K169!. The result that women and men have different risks especially for HIV-1 type 169K motivates further exploratory analyses in the HVTN 702 trial, including assessment of whether sex modifies vaccine efficacy against HIV-1 type 169K.
may yield a moderately improved fit over the Fine–Gray and proportional odds models. The observed direct association with risk of being female in comparison to being male was therefore significantly greater for HIV-1 type 169K than for HIV-1 type K169!. The result that women and men have different risks especially for HIV-1 type 169K motivates further exploratory analyses in the HVTN 702 trial, including assessment of whether sex modifies vaccine efficacy against HIV-1 type 169K.
Table 3.
Time to infection with vaccine-matched virus (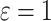 , 169K HIV-1 infection): effect of vaccination and of sex at birth on time to HIV-1 infection; reported are parameter estimates (with standard errors in parentheses) for different semiparametric transformation models and the estimated
, 169K HIV-1 infection): effect of vaccination and of sex at birth on time to HIV-1 infection; reported are parameter estimates (with standard errors in parentheses) for different semiparametric transformation models and the estimated 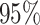 confidence intervals
confidence intervals
| Logarithmic transformation | Box–Cox transformation | |||||
|---|---|---|---|---|---|---|
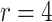
|
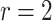
|
PO model | FG model |

|
||
| Loglik |
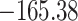
|
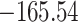
|
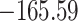
|
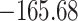
|
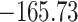
|
|
| Treat |
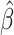
|

|
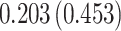
|

|
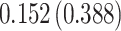
|
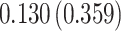
|
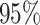 CI
CI |
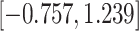
|
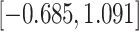
|
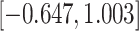
|
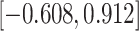
|
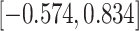
|
|
| Sex |
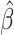
|
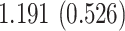
|
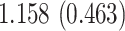
|
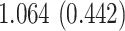
|

|
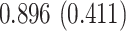
|
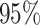 CI
CI |
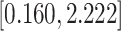
|
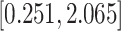
|

|
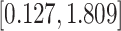
|
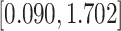
|
|
PO, proportional odds; FG, Fine–Gray; Loglik, loglikelihood; Treat, vaccination treatment; Sex, sex at birth (indicator of female); CI, confidence interval.
Table 4.
Time to infection with vaccine unmatched virus (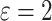 , K169! HIV infection): effect of vaccination and of sex at birth on time to HIV-1 infection; reported are parameter estimates (with standard errors in parentheses) for different semiparametric transformation models and the estimated
, K169! HIV infection): effect of vaccination and of sex at birth on time to HIV-1 infection; reported are parameter estimates (with standard errors in parentheses) for different semiparametric transformation models and the estimated 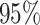 confidence intervals
confidence intervals
| Logarithmic transformation | Box–Cox transformation | |||||
|---|---|---|---|---|---|---|
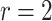
|
PO model | FG model |
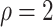
|

|
||
| Loglik |
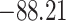
|

|
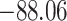
|
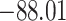
|
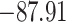
|
|
| Treat |
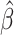
|
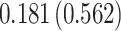
|
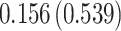
|
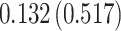
|
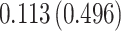
|
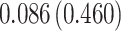
|
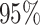 CI
CI |
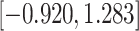
|

|
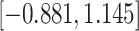
|

|
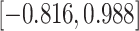
|
|
| Sex |
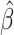
|
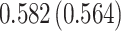
|

|
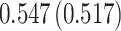
|
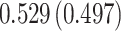
|
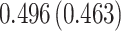
|
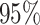 CI
CI |
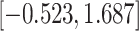
|
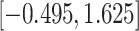
|
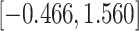
|
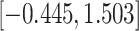
|
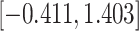
|
|
PO, proportional odds; FG, Fine–Gray; Loglik, loglikelihood; Treat, vaccination treatment; Sex, sex at birth (indicator of female); CI, confidence interval.
Fig. 1.
Model selection with Akaike criterion for the HIV vaccine data: the upper panels are for HIV-1 type 169K and the lower panels for HIV-1 type K169!; the left panels show logarithmic transformation models and the right panels Box–Cox transformation models.
7. Discussion
Any cure model may be interpreted as a competing risks model where the competing risk event is the cure. Therefore, the subdistribution hazard approach proposed in § 2.2 can be applied to any cure model under left-truncation and right-censoring.
A direct relation between the subdistribution hazard and the cumulative incidence function can be established for either time-independent covariates, such as baseline covariates, or external time-dependent covariates. But this is not possible for internal time-dependent covariates, as discussed in Bellach et al. (2019). It is well known that even in survival settings without competing risks, regression parameters for the hazard rate in the presence of internal time-dependent covariates are not interpretable with regard to the underlying distribution; see, for instance, Kalbfleisch & Prentice (2002).
The general regression model can be extended to a model for the marginal mean intensity for recurrent event data with competing terminal events under left-truncation and right-censoring. For the marginal mean intensity, defined as 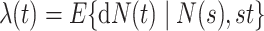 where
where 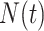 denotes the process counting the number of recurrent events, the usual relationship with the marginal mean is retained; i.e.,
denotes the process counting the number of recurrent events, the usual relationship with the marginal mean is retained; i.e., 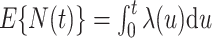 . A slightly modified version of the weighted loglikelihood function (4) may be applied to estimate the regression parameters for the general model for the marginal mean intensity as defined in (3).
. A slightly modified version of the weighted loglikelihood function (4) may be applied to estimate the regression parameters for the general model for the marginal mean intensity as defined in (3).
Supplementary Material
Acknowledgement
The authors thank Erik Parner, Hein Putter, Donglin Zeng and two referees for helpful comments. They also thank the HVTN 503 study participants and personnel. Bellach’s research was in part conducted at the Department of Biostatistics at the University of Copenhagen, Denmark, and supported by the E.U. Programme FP7: Marie-Curie ITN mediasres. Gilbert’s research was supported by the U.S. National Institute of Allergy and Infectious Diseases. The authors received permission to use data from the CASCADE Collaboration in EuroCoord (CASCADE Collaboration, 2006) that was funded by the E.U. Programme FP7, and thank Kholoud Porter, Jannie van der Helm and Ronald Geskus for their support. Kosorok and Fine are also affiliated with the Department of Statistics and Operations Research at the University of North Carolina, Chapel Hill.
Appendix
Model conditions
Condition A1.
The cumulative baseline
is a strictly increasing and continuously differentiable function, and
lies in the interior of a compact set
.
Condition A2.
The vector of covariates
is with probabilty one of bounded variation on the observed interval
. In combination with Condition A1 this implies that there is a constant
such that
.
Condition A3.
The endpoint of the study
is chosen in such a way that with probability one there exists a constant
such that
and
. There is a finite partition
of the interval
with
for some
.
Condition A4.
The function
is thrice continuously differentiable and strictly increasing, with
,
and
. Moreover, one of the following conditions holds:
(i)
for
;
for
and, in addition, for any
and any sequence
with
as
,
(A1)
Condition A5.
(Identifiability). If a vector
and a deterministic function
,
, exist such that
with probability one, then
and
for
-almost all
, where
denotes Lebesgue measure. This condition rules out perfect multicollinearity of the covariates
for
-almost all
.
Condition A6.
Let
denote a vector in
and let
. For a subset
of nonzero Lebesgue measure, for all
we have that
Existence of the weighted nonparametric maximum likelihood estimator and consistency
We first ascertain that 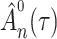 is bounded almost surely on
is bounded almost surely on 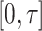 . As a consequence, all estimated jump sizes must be finite. By the Helly–Bray lemma we obtain that for every sequence
. As a consequence, all estimated jump sizes must be finite. By the Helly–Bray lemma we obtain that for every sequence 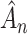 there exist a subsequence
there exist a subsequence 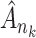 and
and 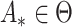 such that
such that 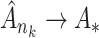 . Together with Condition A1 this implies sequential compactness for
. Together with Condition A1 this implies sequential compactness for 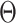 , which means that for every sequence
, which means that for every sequence 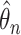 there exist a subsequence
there exist a subsequence 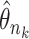 and
and 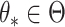 such that
such that 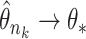 . Using a Kullback–Leibler argument, one can then conclude that every subsequence converges to the true parameter
. Using a Kullback–Leibler argument, one can then conclude that every subsequence converges to the true parameter 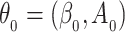 . As
. As 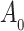 is a continuous and increasing function, we obtain uniform almost sure convergence for the cumulative baseline hazard
is a continuous and increasing function, we obtain uniform almost sure convergence for the cumulative baseline hazard 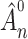 and almost sure convergence for
and almost sure convergence for 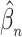 .
.
Let 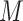 be a constant such that
be a constant such that 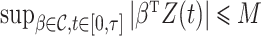 . We define
. We define 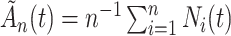 and consider the sequence
and consider the sequence 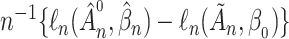 . Under Condition A4(i) the sequence is bounded above by
. Under Condition A4(i) the sequence is bounded above by
 |
and under Condition A4(ii) the sequence is bounded above by
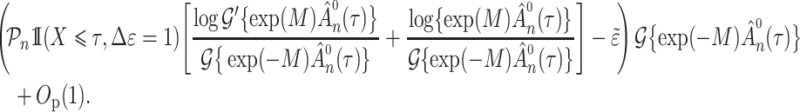 |
In both cases the upper bound would become infinitely small if 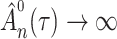 , which means that
, which means that 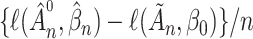 would go to
would go to 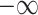 as
as 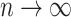 . This contradicts the definition of
. This contradicts the definition of  as a maximum likelihood estimator. Therefore
as a maximum likelihood estimator. Therefore 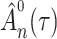 is bounded almost surely on
is bounded almost surely on 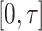 .
.
Writing 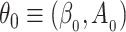 and
and 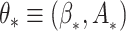 , we define the Kullback–Leibler distance for the cure model with independent left-truncation and right-censoring as
, we define the Kullback–Leibler distance for the cure model with independent left-truncation and right-censoring as
 |
where 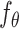 is the subdistribution density for the event of interest. In the Supplementary Material we prove that
is the subdistribution density for the event of interest. In the Supplementary Material we prove that 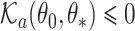 and
and 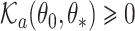 , and establish the identifiability, namely that if
, and establish the identifiability, namely that if 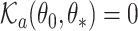 then
then 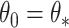 . For the competing risks model with independent left-truncation and right-censoring, we define
. For the competing risks model with independent left-truncation and right-censoring, we define
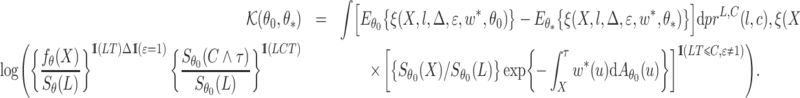 |
Consistency then follows from the asymptotic equivalence of 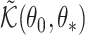 and
and 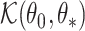 .
.
Weak convergence to a Gaussian process
Let 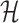 denote the space of elements
denote the space of elements 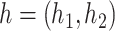 with
with 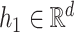 and
and 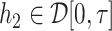 . A norm on
. A norm on 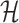 is then defined by
is then defined by  , where
, where  denotes the Euclidean norm and
denotes the Euclidean norm and 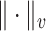 the total variation norm. For
the total variation norm. For 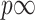 we define
we define  . The parameter space is
. The parameter space is  . For
. For 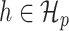 we define
we define 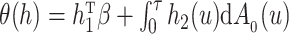 , so that
, so that 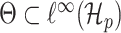 . One-dimensional submodels of the form
. One-dimensional submodels of the form 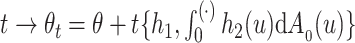 are considered with
are considered with 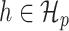 to define the empirical score operator
to define the empirical score operator
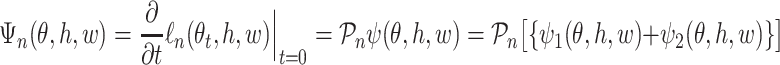 |
for a measurable function 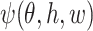 , where
, where 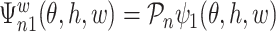 is the component related to the derivative with respect to
is the component related to the derivative with respect to 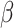 and
and 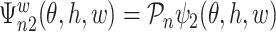 is the component related to the derivative along the submodel for
is the component related to the derivative along the submodel for 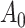 , as stated in the Supplementary Material. The limiting version
, as stated in the Supplementary Material. The limiting version 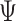 is defined by replacing the empirical measure
is defined by replacing the empirical measure 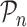 by the probability measure
by the probability measure 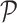 . It is then sufficient to verify the conditions of Lemma S2 in the Supplementary Material for weighted
. It is then sufficient to verify the conditions of Lemma S2 in the Supplementary Material for weighted 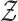 -estimators.
-estimators.
To verify condition  in Lemma S2, note that as our model is based on independent and identically distributed observations, it is sufficient to verify the two conditions of Lemma S3. Arguments like those in van der Vaart & Wellner (1996) and Kosorok (2008) along the lines of Donsker preservation theorems are immediately applicable. The second condition of Lemma S3 immediately follows, as pointwise convergence can be strengthened to
in Lemma S2, note that as our model is based on independent and identically distributed observations, it is sufficient to verify the two conditions of Lemma S3. Arguments like those in van der Vaart & Wellner (1996) and Kosorok (2008) along the lines of Donsker preservation theorems are immediately applicable. The second condition of Lemma S3 immediately follows, as pointwise convergence can be strengthened to 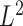 convergence by dominated convergence. By the Donsker theorem,
convergence by dominated convergence. By the Donsker theorem,  converges in distribution to the tight random element
converges in distribution to the tight random element 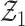 . Also by the Donsker theorem,
. Also by the Donsker theorem, 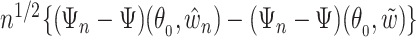 converges in distribution to a tight random element
converges in distribution to a tight random element 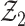 . Joint convergence follows from the asymptotic linearity of the two components marginally, together with the fact that the composition of two Donsker classes is also Donsker. By definition
. Joint convergence follows from the asymptotic linearity of the two components marginally, together with the fact that the composition of two Donsker classes is also Donsker. By definition  . As argued in Parner (1998), from the Kullback–Leibler information being positive and by interchanging expectation and differentiation, we obtain
. As argued in Parner (1998), from the Kullback–Leibler information being positive and by interchanging expectation and differentiation, we obtain 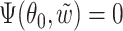 .
.
To show continuous invertibility of 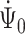 and
and 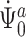 , it suffices to prove the invertibility of the operator
, it suffices to prove the invertibility of the operator 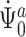 corresponding to the cure model, as the scores for the cure model and for the competing risks model with left-truncation and right-censoring are asymptotically equivalent. Therefore,
corresponding to the cure model, as the scores for the cure model and for the competing risks model with left-truncation and right-censoring are asymptotically equivalent. Therefore, 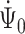 and
and 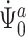 are also asymptotically equivalent. The continuous Gateaux derivatives are provided in the Supplementary Material. Gateaux differentiability can be strengthened to Frechét differentiability with an additional continuity condition.
are also asymptotically equivalent. The continuous Gateaux derivatives are provided in the Supplementary Material. Gateaux differentiability can be strengthened to Frechét differentiability with an additional continuity condition.
Thus, from Lemma S2 we obtain weak convergence of 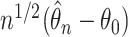 , and the covariances for the limiting process
, and the covariances for the limiting process 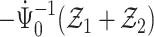 with
with 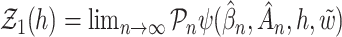 and
and 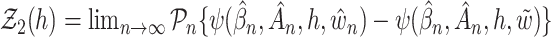 are
are
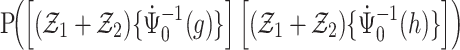 |
for 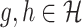 (Kosorok, 2008).
(Kosorok, 2008).
Supplementary material
Supplementary material available at Biometrika online includes proofs of Theorems 1 and 2, details on the sandwich estimator for the variance, results of additional simulation studies, and a proof of the equivalence of the weights proposed by Geskus (2011) and Zhang et al. (2011).
References
- Andersen, P. K., Borgan, Ø., Gill, R. D. & Keiding, N. (1988). Censoring, truncation and filtering in statistical models based on counting processes. Contemp. Math. 80, 19–60. [Google Scholar]
- Andersen, P. K., Borgan, Ø., Gill, R. D. & Keiding, N. (2013). Statistical Models Based on Counting Processes. New York: Springer. [Google Scholar]
- Bellach, A., Kosorok, M. R., Rüschendorf, L. & Fine, J. P. (2019). Weighted NPMLE for the subdistribution of a competing risk. J. Am. Statist. Assoc. 114, 259–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CASCADE Collaboration (2006). Effective therapy has altered the spectrum of cause-specific mortality following HIV seroconversion. AIDS 20, 741–9. [DOI] [PubMed] [Google Scholar]
- Chen, K., Jin, Z. & Ying, Z. (2002). Semiparametric analysis of transformation models with censored data. Biometrika 89, 659–68. [Google Scholar]
- Fine, J. P. (2001). Regression modeling of competing crude failure probabilities. Biostatistics 2, 85–97. [DOI] [PubMed] [Google Scholar]
- Fine, J. P. & Gray, R. J. (1999). A proportional hazards model for the subdistribution of a competing risk. J. Am. Statist. Assoc. 94, 496–509. [Google Scholar]
- Geskus, R. B. (2011). Cause-specific cumulative incidence estimation and the Fine and Gray model under both left truncation and right censoring. Biometrics 67, 39–49. [DOI] [PubMed] [Google Scholar]
-
Gray, R. J. (1988). A class of
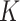 -sample tests for comparing the cumulative incidence of a competing risk. Ann. Statist. 16, 1141–54. [Google Scholar]
-sample tests for comparing the cumulative incidence of a competing risk. Ann. Statist. 16, 1141–54. [Google Scholar] - He, S. & Yang, G. L. (1998). Estimation of the truncation probability in the random truncation model. Ann. Statist. 26, 1011–27. [Google Scholar]
- Juraska, M., Magaret, C. A., Shao, J., Carpp, L. N., Fiore-Gartland, A., Benkeser, D., Girerd-Chambaz, Y., Langevin, E., Frago, C., Guy, B. et al. (2018). Viral genetic diversity and protective efficacy of a tetravalent dengue vaccine in two phase 3 trials. Proc. Nat. Acad. Sci. 115, E8378–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalbfleisch, J. D. & Prentice, R. L. (2002). The Statistical Analysis of Failure Time Data. Hoboken, New Jersey: John Wiley & Sons, 2nd ed. [Google Scholar]
- Keiding, N. & Gill, R. D. (1990). Random truncation models and Markov processes. Ann. Statist. 18, 582–602. [Google Scholar]
- Kosorok, M. R. (2008). Introduction to Empirical Processes and Semiparametric Inference. New York: Springer. [Google Scholar]
- Murphy S. A. (1994). Consistency in a proportional hazards model incorporating a random effect. Ann. Statist. 22, 712–31. [Google Scholar]
- Murphy S. A. (1995). Asymptotic theory of the frailty model. Ann. Statist. 23, 182–98. [Google Scholar]
- Owen, A. B. (2001). Empirical Likelihood. Boca Raton, Florida: Chapman & Hall/CRC. [Google Scholar]
- Parner, E. (1998). Asymptotic theory for the correlated gamma-frailty model. Ann. Statist. 26, 183–214. [Google Scholar]
- R Development Core Team (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0. http://www.R-project.org. [Google Scholar]
- Rolland, M., Edlefsen, P. T., Larsen, B., Tovanabutra, S., Sanders-Buell, E., Hertz, T., Decamp, A. C., Carrico, C., Menis, S., Magaret, C. A. et al. (2012). Increased HIV-1 vaccine efficacy against viruses with genetic signatures in Env V2. Nature 490, 417–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Vaart, A. W. & Wellner, J. A. (1996). Weak Convergence and Empirical Processes. New York: Springer. [Google Scholar]
- Zeng, D. & Lin, D. Y. (2006). Efficient estimation of semiparametric transformation models for counting processes. Biometrika 93, 627–40. [Google Scholar]
- Zhang, X., Zhang, M. J. & Fine, J. P. (2009). A mass redistribution algorithm for right-censored and left-truncated time to event data. J. Statist. Plan. Infer. 139, 3329–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, X., Zhang, M. J. & Fine, J. P. (2011). A proportional hazards regression model for the subdistribution with right-censored and left-truncated competing risks data. Statist. Med. 30, 1933–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.