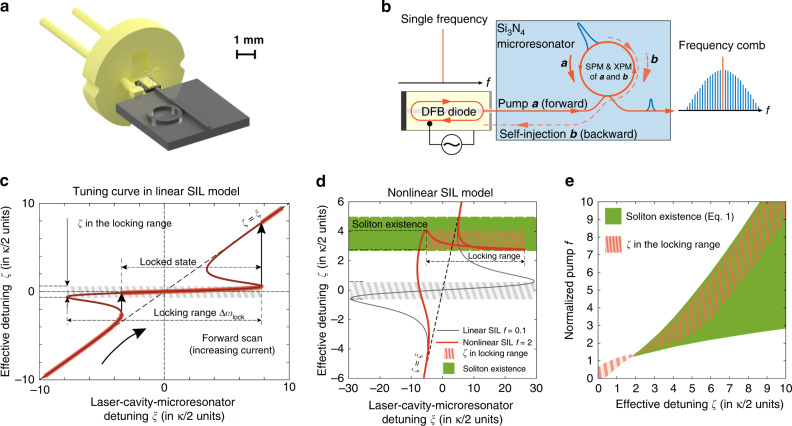
Fig. 1. Scheme of a compact soliton microcomb using laser self-injection locking.

a Illustration of the soliton microcomb device via direct butt coupling of a laser diode to the Si₃N₄ chip. b Principle of laser self-injection locking. The DFB laser diode is self-injection locked to a high-Q resonance via Rayleigh backscattering and simultaneously pumps the nonlinear microresonator to generate a soliton microcomb. In this work, we introduce and study the influence of the microresonator nonlinearity (self- and cross- phase modulation) on the SIL. Nonlinear SIL model explains the dynamics of the soliton formation in this case. c Schematic of the self-injection locking dynamics without taking into account the microresonator nonlinearity, i.e., linear SIL model. The injection current defines the laser cavity frequency ω_LC and the laser cavity-microresonator detuning ξ = 2(ω₀ − ω_LC)/κ ~ I_inj − I₀, while the whole system oscillates at the actual laser emission frequency ω_eff, detuned from the cold microresonator at the ζ = 2(ω₀ − ω_eff)/κ. We call the dependence of the laser emission frequency on the injection current, or ζ dependence on ξ, a tuning curve. The normalized effective detuning ζ deviates from ξ = ζ (free-running case) when self-injection locking occurs. The slope of the tuning curve dζ/dξ ≪ 1 is observed within the locking range, providing narrowing of the laser diode linewidth. Note, that $\zeta \in \left[-0.7;0.7\right]$ in the locked state for the linear SIL model and is not enough for soliton formation for any pump power. d Nonlinear SIL model coincides with the linear one for low pump powers f < 1, but the tuning curve changes significantly at higher pump power f > 1 and shifts up. e Our model predicts that attainable ζ values in the SIL regime are red-detuned and located inside the soliton existence range (Eq. (1)).