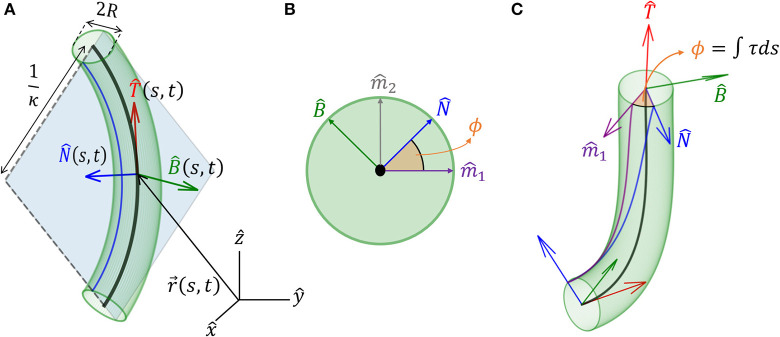
Figure 1.

Geometrical definitions for a 3D cylindrical organ. (A) A cylindrical organ of constant radius R is described by its centerline, parameterized by the arc-length s. $\overrightarrow{r}(s,t)$ denotes the Cartesian position of a point along the centerline at point s and time t. The local Frenet-Serret frame at some point along the centerline is defined by the tangent vector $\widehat{T}(s,t)=\partial \overrightarrow{r}(s,t)/\partial s$, its derivative the normal vector $\widehat{N}(s,t)$ (Equation 2), and the bi-normal vector $\widehat{B}(s,t)$ (Equation 3). Here, the organ has a constant curvature κ and is restricted to a plane, illustrating 1/κ(s, t) as the radius of curvature. (B) Cross-section of the organ and the natural frame: ($\widehat{N}$, $\widehat{B}$) span the cross-section, (${\widehat{m}}_1$, ${\widehat{m}}_2$) are constant vectors defining the natural frame, as described in section 3, and ϕ(s, t) defines the angle between $\widehat{N}$ and the reference vector ${\widehat{m}}_1$. (C) An organ not restricted to a plane. Here ϕ(s, t) changes along s, and torsion is defined as τ = ∂ϕ/∂s. Note that in (A), τ = 0.