Figure 3.

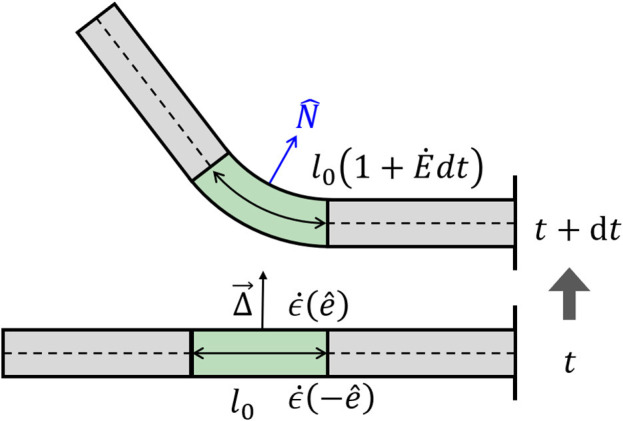
Differential growth. Differences in growth rates across a cylinder lead to a change in curvature. At time t, we have a straight organ with κ(t) = 0 and with a growth zone in the center of length l(t) = l₀, marked in green. The differential growth vector $\overrightarrow{\Delta }$ in the growth zone is constant and points upwards in the $\widehat{e}$ direction. Following Equation (7), the growth rate on the lower side is higher than that in the upper side $\stackrel{.}{ϵ}(-\widehat{e})<\stackrel{.}{ϵ}(\widehat{e})$, and after a time interval dt, the two sides grow different amounts, leading to bending of the growth zone with a new curvature κ(t + dt) > 0. The new length of the growth zone along the centerline is now l(t + dt) = l₀(1 + $\stackrel{.}{E}$dt). Note that changes in curvature in the middle of the organ lead to changes in orientation of the rest of the organ.