Relationship between dosimetric leaf gap and dose calculation errors for high definition multi-leaf collimators in radiotherapy

Abstract

Background and purpose

Dosimetric leaf gap (DLG) is a parameter to model the round-leaf-end effect of multi-leaf collimators (MLC) that is important for treatment planning dose calculations in radiotherapy. In this study we investigated on the relationship between the DLG values and the dose calculation errors for a high-definition MLC.

Materials and methods

Three sets of experiments were conducted: (1) physical DLG measurements using sweeping-gap technique, (2) DLG adjustment based on spine radiosurgery plan measurements, and (3) DLG verification using films and ion-chambers (IC). All experiments were conducted on a Varian Edge machine equipped with HD120 MLC for 6X, 6XFFF, and 10XFFF (FFF: flattening filter free). The Analytical Anisotropic Algorithm was used for all dose calculations.

Results

The measured physical DLGs were 0.39 mm, 0.27 mm, and 0.42 mm for 6X, 6XFFF, and 10XFFF respectively. The calculated doses were lower by 4.2% (6X), 3.7% (6XFFF), and 6.8% (10XFFF) than the measured, while the adjusted DLG values with minimum errors were 1.1 mm, 0.9 mm, and 1.5 mm. The IC measurement errors were < 1%, and the film gamma pass rates (3%/3 mm) were greater than 97% for the spine plans.

Conclusions

The calculated doses were systematically lower than measured doses with the physical DLG values. It was necessary to increase the DLG values to minimize the dose calculation uncertainty. The optimal DLG values may be specific to individual MLCs and beams and, thus, careful evaluation and verification are warranted.

1. Introduction

Multi-leaf collimator (MLC) is an important component of a modern linear accelerator, delivering intensity modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT) with individual leaves sweeping across treatment fields. Accurate modeling is of great importance for modern radiation therapy, especially for intracranial stereotactic radiosurgery (SRS) and extracranial stereotactic body radiation therapy (SBRT), where an ablative dose is delivered in a single or in only a few treatment sessions. Due to the nature of small SRS and SBRT target volumes, micro- or high-definition (HD) MLCs, i.e. MLCs with fine leaf width, are desired to improve the prescription isodose-to-target conformity [1], [2], [3].

American Association of Physicists in Medicine (AAPM) Task Group (TG) Report 72 provides different types of MLC designs, physical properties, and quality assurance (QA) recommendations [4]. AAPM TG Report 142 recommends routine MLC quality assurance tasks [5]. In addition to the MLC commissioning and QA prior to its clinical usage, MLCs need to be properly modeled in the treatment planning system (TPS) for accurate dose calculation. Despite the complex MLC designs, beam quality variations, and intensity changes across the fields, TPSs usually take a simple approach with a small number of parameters for modeling, including dosimetric leaf gap (DLG) and mean transmission factor. The mean transmission factor is the percentage of radiation passing through and between the MLC leaves. The DLG takes into account the difference between the nominal leaf positions and the radiological leaf positions to incorporate the round-leaf-end effect in dose calculations. It also incorporates the minimal physical gap between leaves to prevent collision.

For DLG measurements, the sweeping gap technique [6] is most widely used in clinics. However, there have been reports where the measured DLG values for an HD MLC were found clinically unacceptable [7], [8]. Further, the cause of the discrepancy is unknown to date [8]. In this study, we present our experiment results to quantify the discrepancy and to find the relationship between the DLG values and the dose calculation errors of an HD MLC mounted on a radiosurgery treatment unit. In this report, the term “error” is loosely defined as the difference between the calculated and measured doses.

2. Materials and methods

2.1. Linear accelerator, MLC, and dose calculation algorithm

All experiments were conducted on a Varian Edge machine equipped with an HD120 MLC (Varian Medical System, Palo Alto, CA). The machine has two flattening-filter-free (FFF) 6X and 10X photon modes in addition to a conventional flattened 6X. Their respective maximum dose rates are 1400, 2400, and 600 monitor units (MU) per minute. The HD120 MLC has 120 leaves. The central 64 leaves (32 leaf pairs) and the outer 56 leaves (28 leaf pairs) have the projection leaf width of 2.5 mm and 5.0 mm at source-axis distance of 100 cm, respectively. Thus, the resulting maximal field height is 22 cm (= 28 * 0.5 + 32 * 0.25 = 14 + 8 cm). The maximum field size is 22 × 40 cm² for static fields and 22 × 32 cm² for intensity-modulated fields. Other related parameters are listed in the supplementary material Table S1. All dose distributions were calculated in Eclipse TPS (Varian Medical Systems Inc., Palo Alto, CA) using Analytical Anisotropic Algorithm (AAA, v13.6.23).

2.2. Physical DLG measurement via sweeping-gap dynamic MLCs

A plastic cube phantom with a size of 15 × 15 × 15 cm³ (Reinstein EZ-Cube Phantom, Radiation Products Design, Inc., Albertville, MN) was setup on the treatment table with source-to-surface distance (SSD) of 100 cm. A 0.6 cc Farmer ionization chamber (PTW TN30006-0379, Freiburg, Germany) was placed perpendicular to the leaf-traveling direction in the phantom at a depth of 2.5 cm. The chamber sensitive volume was 23.6 mm long with 6.1 mm diameter. The dose conversion factor $N_{\mathit{dw}}^{\mathit{co}60}$ was 5.433 Gy/C, calibrated at an ADCL (Accredited Dosimetry Calibration Laboratory) in 2015. For each energy, the phantom was exposed to radiation beams with MLCs open, closed, and dynamic sweeping gaps of 2, 4, 6, 10, 14, 16, and 20 mm [6]. For all beams, the jaws were set to 10 × 10 cm² and delivered 100 MU. Then, the net charge without the transmission radiation at the sweeping gap g, $Q_{\mathit{net}}(g)$ was calculated as:

$$Q_{\mathit{net}}(g)=Q(g)-Q_T\left(\frac{L-g}{L}\text{,}\right)$$

where the Q($g$) was the total charge collected for the beam with the gap $g$, and the second term was the transmitted charge when the detector was blocked by the MLC leaves. The mean charge from radiation transmitted through the MLC leaves $Q_T$ was measured as:

$$Q_T=(Q_{\mathit{closed}.\mathit{bankA}}+Q_{\mathit{closed}.\mathit{bankB}})/2.0$$

where $Q_{\mathit{closed}.\mathit{bankA}/B}$ are respectively the collected charges with MLC leaves closed by bank A and B. The vendor provided MLC plans had sixteen control points, which was sufficient for proper off-axis leaf position correction [9]. The travel length was 120 mm for all dynamic sweeping gaps. The $Q_{\mathit{net}}(g)$ was then plotted and fitted as a linear function of $g$ and measured the intersection on the horizontal axis of $g$ as DLG; i.e., $\arg (g)\to Q_{\mathit{net}}(g)=0$.

2.3. Optimal DLG determined with IC measurements for spine SBRT plans

Five spine SBRT plans at the vertebra of C5, C2, C6, T1, and L4 were selected from previously treated patients. All plans were VMAT with two or three full arcs. Each plan was re-optimized with the use of 6X, 6XFFF, 10XFFF for a same prescription dose of 16 Gy in one fraction. Thus, a total fifteen plans were created and then mapped to a stereotactic QA phantom (PMMA, StereoPhan, Sun Nuclear, Melbourne, FL) using AAA dose calculation algorithm. The phantom was repositioned on the treatment table according to the 3D/3D automatic CBCT co-registration with the reference planning CT image. The doses at the isocenter for individual plans were measured using a 0.015 cc PinPoint ion-chamber of 5 mm length and 2 mm diameter (TN31006, PTW, Freiburg, Germany). The chamber calibration factor was obtained in the same way as AAPM TG119, i.e., by correlating the measured charge of two opposing beams to the AAA calculated dose. The optimal DLG value per energy was determined by analyzing the measured isocenter dose with planned isocenter doses at four different DLG values.

2.4. Validation of optimal DLG with EBT3 film dosimetry on spine plans

To validate the optimal DLG values, transmission factors, and other MLC configurations in Eclipse TPS, the 15 spine plans (5 sites × 3 energies) were delivered to a polystyrene phantom for 2D dose distribution measurements using 8″ × 10″ radio-chromic films (Gafchromic EBT3, Radiation Product Design Inc., Albertville, MN) [10]. Films were scanned using a flatbed document scanner in positive film transmission mode with 75 DPI, RGB per pixel, and 16 bit per color. The pixel values in the green and red channels were converted to optical density as $\mathit{OD}=-{\mathit{log}}_{10}(\mathit{pixel}\mathit{value}/65535)$. The OD values, then, converted to doses using calibration curves (see Supplementary material for the details of film calibration). The average of the red and green doses were used as the final film dose; $D=(D_{\mathit{red}}+D_{\mathit{green}})/2$. The post-irradiation colorization time was kept to be greater than 12 h for all films, and one calibration film was exposed for each measurement session to minimize dosimetry uncertainty. Gamma analysis of 3% dose difference (DD) and 3 mm distance to agreement (DTA) was used to measure the similarity between the film and plan dose distributions [11].

2.5. Validation – IC measurements on lung and liver SBRT and brain SRS plans

In addition to the spine plans, the machine is used for other types of stereotactic treatments. In order to validate the chosen DLG values, ten lung and liver SBRT and five brain SRS plans were randomly selected from previously treated patient database, and measured the delivery errors using the stereotactic QA phantom and PinPoint ion-chamber (TN31006, PTW, Freiburg, Germany). For all plans, the chamber volume was contoured as a cylinder (2 mm diameter × 5 mm height) and the mean dose of the volume was compared to the corresponding measured dose. All plans were VMAT and their plan properties are presented in the Supplementary material Table S2.

2.6. Validation – IC measurements on AAPM TG199 IMRT plans

To be complete, we also measured errors on five regular IMRT plans using the data sets (CT, contour set, and dose criteria) from AAPM Task Group 119 [12]. They consisted of prostate, head and neck, multi-target, hard and easy C shape plans with 7–9 static gantry IMRT beams. The plans were mapped to stereotactic QA phantom (PMMA, StereoPhan, Sun Nuclear, Melbourne, FL), and the errors in seven dose regions were measured using the PinPoint ion-chamber. As suggested by the task group report, the chamber was calibrated for dosimetry using the TPS doses of AP/PA square beams.

2.7. Dose error dependency on sweeping gap and jaw size

As Kielar et al. [8] noted the cause was yet unknown as to why the TPS doses were lower in plan QA measurements for HD120 MLC when the measured physical DLG values were used for dose calculations. In order to better understand the source of errors, we repeated the sweeping gap MLC measurements for 6XFFF with gaps extended up to 100 mm. A solid water phantom with a calibrated Farmer chamber (0.6 cc) was used with settings of 10 × 10 cm² field size, 95 cm SSD, and 5 cm depth. The corresponding doses were calculated in Eclipse with the final DLG value of 0.9 mm for comparison. The same set of measurements were repeated with different jaw sizes of 5 × 5, 10 × 10, 15 × 15 to 20 × 20 cm² to understand the dose error dependency on the jaw sizes.

3. Results

3.1. DLG values and transmission factors

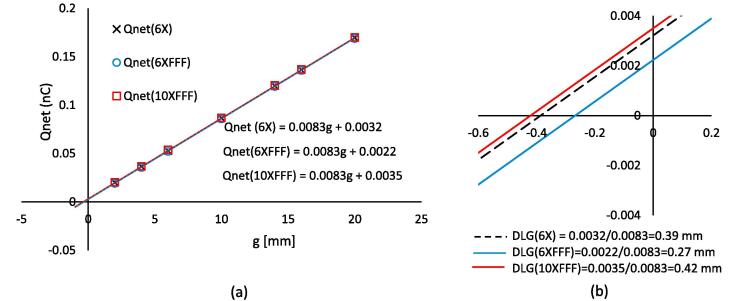
Fig. 1a plots the net charge collected in the ion-chamber, Q_net [nC], as a function of sweeping gap g [mm]. The fitted lines for 6X, 6XFFF, and 10XFFF had the same slope of 0.0083 nC/mm, indicating the same net charge increase per unit gap increase. The estimated net charges with zero MLC gap (the line intersections with the Q_net axis) were 3.2 pC, 2.2 pC, and 3.5 pC for 6X, 6XFFF, and 10XFFF respectively (Fig. 1b). The calculated DLG values (the line intersections with the g axis) were 0.39 mm, 0.27 mm, and 0.42 mm respectively for 6X, 6XFFF, and 10XFFF. The measured transmission factors of three energies were 1.1%, 0.9%, and 1.1%.

Fig. 1.

DLG plots for 6X, 6XFFF, and 10XFFF; (a) plots of net charge Q_net as a function of sweeping leaf gap g and (b) the zoom-in view of plot (a) near the intersections. The R² was 1.0 for all three line fittings.

3.2. DLG adjustment – IC measurements on spine plans

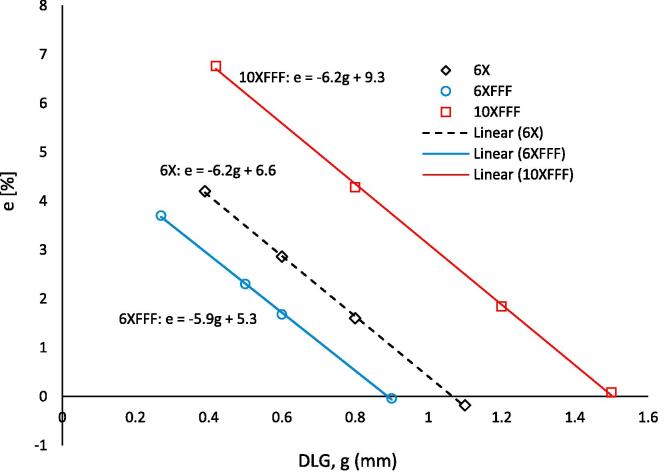
The measured doses for spine SBRT plans were higher by 4.2% (6X), 3.7% (6XFFF), and 6.8% (10XFFF) than the corresponding plan doses when the physical DLG values were used for dose calculations (Table 1, Fig. 2). The errors decreased as DLG increased at rates of 6.2%/mm for both 6X and 10XFFF and 5.9%/mm for 6XFFF. Based on the plots in Fig. 2, the optimal DLG values (the intersections with the DLG axis) were 1.1 mm for 6X, 0.9 mm for 6XFFF, and 1.5 mm for 10XFFF. The small remaining dose errors of −0.2% (6X), 0.0% (6XFFF), and −0.1% (10XFFF) confirmed the optimal DLG values. On the other hand, the intersections with the y axis (the estimated errors with zero DLG values) were 6.6% (6X), 5.3% (6XFFF), and 9.3% (10XFFF). The final DLG values, transmission factors, and other MLC related parameters entered in our planning system are available in the Supplementary material Table S3.

Table 1.

Measured and calculated dose differences of five spine SBRT plans with four DLG values per energy. The underlined bold numbers are the final DLG values and the corresponding mean errors. Error (%) = (measure dose − plan dose)/plan dose × 100.

	6X				6XFFF				10XFFF
DLG (mm)	0.39	0.6	0.8	1.1	0.27	0.5	0.6	0.9	0.42	0.8	1.2	1.5
SBRT1	4.2	2.8	1.4	−0.5	4.5	3.1	2.5	0.8	8.4	5.5	2.6	0.5
SBRT2	2.0	1.5	1.0	0.3	2.0	1.4	1.2	0.5	3.8	2.8	1.9	1.2
SBRT3	4.2	2.2	0.4	−2.2	3.9	2.0	1.1	−1.3	7.9	4.2	0.7	−1.8
SBRT4	6.6	5.3	4.1	2.3	5.1	3.7	3.1	1.4	8.1	5.6	3.1	1.3
SBRT5	4.0	2.5	1.1	−0.8	3.0	1.3	0.5	−1.6	5.6	3.3	0.9	−0.8
Mean	4.2	2.9	1.6	−0.2	3.7	2.3	1.7	0.0	6.8	4.3	1.8	0.1

Fig. 2.

Measured and calculated dose differences for five spine plans as a function of DLG (g) for 6X, 6XFFF, and 10XFFF; e = (D_IC − D_TPS)/D_TPS × 100; D_IC – measured dose using ion chamber and D_TPS – calculated dose in TPS. Each data point is the mean error of five measurements at given DLG. All three R2 values were equal to 1.0.

3.3. Validation – EBT3 film dosimetry on spine plans

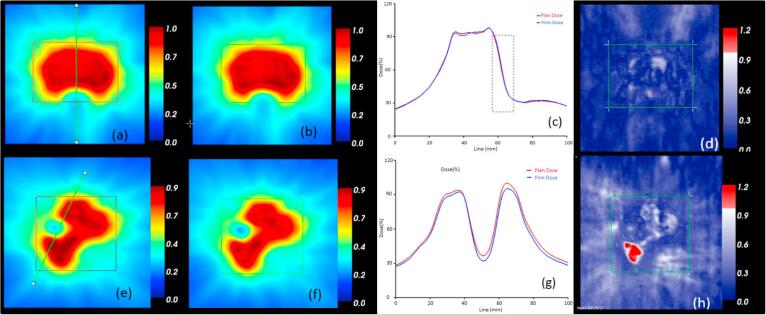
The gamma pass rates ($\gamma$ < 1.0, 3%/3 mm) of the EBT3 film analysis ranged from 97% to 100% (Supplementary material Table S4). The lowest pass rates were 98% for 6X, 99% for 6XFFF, and 97% for 10XFFF. In the relative magnitude of film doses with respect to the corresponding plan doses, the film doses were overall slightly lower than plan doses, except the 1% higher SBRT1 case for 6XFFF. The largest difference was 5% for SBRT3 (10XFFF). The dose distributions and gamma maps of the best and worst cases are shown in Fig. 3. The SBRT1 (6XFFF) case had a good agreement between the film and plan doses with 100% gamma pass rate. The dose agreement in the sharp dose fall off region from the planning target volume (PTV) to the spinal cord was very good (Fig. 3c). For the SBRT3 case, the gamma pass rate in the high dose region was 97%. The posterior region of PTV failed as shown red in the gamma map (Fig. 3 h). With the film dose scaled up by 5%, i.e. in a relative gamma analysis, the gamma pass rate became 100%.

Fig. 3.

Two example EBT3 film dosimetry results; (a–d) SBRT1 (6XFFF) – case with smallest difference; (from left) plan dose, film dose, profile, and gamma map, (e–h) SBRT3 (10XFFF) – case with the largest difference.

3.4. Validation – lung and liver SBRT and brain SRS plans

The measurement errors for the ten lung and liver SBRT and five brain SRS plans were small with a mean difference of −0.2% (Supplementary material Table S2). The largest error was −2.3% for a brain case (Brain 1). The error was likely due to its small PTV volume (0.3 cc). The two 10XFFF liver plans had small errors as well; −0.2% and −1.7% respectively.

3.5. Validation – IC measurements on AAPM TG199 IMRT plans

The measurement errors for the AAPM TG199 IMRT plans were in the range of −1.8% to 0.8% (Supplementary material Table S5). The errors in the intermediate and high dose regions were all <1.0%. The mean and standard deviation (SD) of the errors were −0.3% and 0.9% respectively. The corresponding 95% confident limit (CL = |mean| ± 1.96SD) was 2.0.

3.6. Dose error dependency on sweeping gap and jaw size

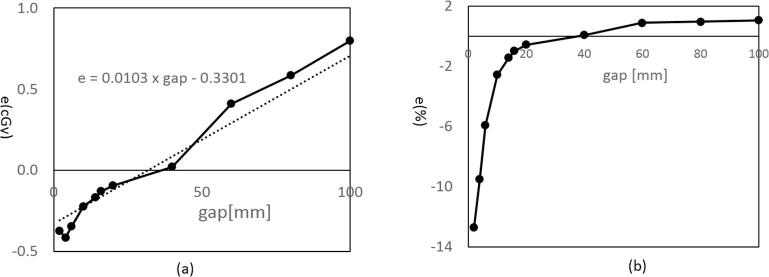
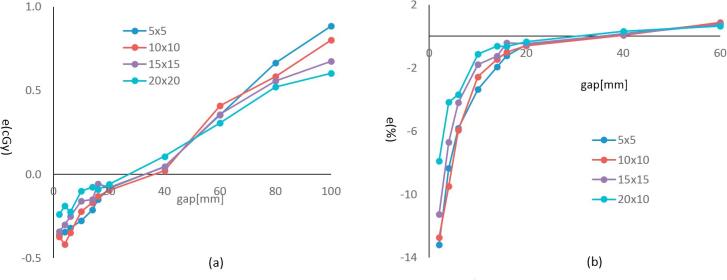
The dose discrepancy between the calculated and measured doses was a function of gap as shown in Fig. 4. The measured doses were lower than calculated for the small sweeping gaps while it was larger for the large gaps. The zero-crossing occurred at gap 32 mm. In a relative scale (Fig. 4b), the differences were bigger with small gaps due to the small corresponding plan doses. At the 2 mm gap, the error reached down to -12.5%. With the larger gaps, the absolute error was larger, but the relative error was small (<1%) because of the relatively larger doses. When the sweeping gap was small, the fraction of time the ion-chamber saw the radiation source was very small (1.6% of total time for 2 mm gap), and for the most of time the chamber was blocked by the MLC leaves. Therefore, the errors are expected to come mostly from the uncertainties in the scatter dose estimation. Fig. 5 shows the measurement results with the same set of sweeping gaps, but with different jaw sizes of 5 × 5, 10 × 10, 15 × 15 to 20 × 20 cm². As shown, the errors were also affected by the jaw settings, where the larger errors were associated with the smaller jaw openings.

Fig. 4.

Measured and calculated dose differences for dynamic sweeping gap MLCs with gaps of 2, 4, 6, 10, 14, 16, 20, 40, 60, 80, and 100 mm; dose differences in (a) absolute and (b) relative scales; FS = 10 × 10 cm², SSD = 95 cm, depth = 5 cm, solid water phantom, 0.6 cc farmer chamber, and energy = 6XFFF.

Fig. 5.

Measured and calculated dose differences for dynamic sweeping gap MLCs with jaw field sizes of 5 × 5, 10 × 10, 15 × 15, and 20 × 20 cm² in (a) absolute and (b) relative scales; SSD = 95 cm, depth = 5 cm, solid water phantom, 0.6 cc farmer chamber, and energy = 6XFFF.

4. Discussion

Measuring DLG using the sweeping gap MLC patterns is widely used in clinics. It is a convenient way of measuring DLG using an ion-chamber with a simple phantom. There is no need of cumbersome film processing, which is often used for measuring static radiation field offset (RFO, roughly the half of DLG) [8]. For convenience, the vendor provided the MLC files and the procedure guideline for the sweeping gap DLG measurement as well. However, as clearly shown in this study, it was necessary to adjust the measured physical DLG values to reduce dose calculation errors for the system investigated. Using the original measured DLG values (0.39 mm/6X, 0.27 mm/6XFFF, and 0.42 mm/10XFFF), the TPS underestimated the doses by 4.2% ∼ 6.8% on average for spine SBRT plans (Fig. 2), which is not clinically acceptable. In order to reduce the errors, it was necessary to increase the DLG values by factors of 2.8, 3.3, and 3.6 for respective energies (1.1 mm/6X, 0.9 mm/6XFFF, and 1.5 mm/10XFFF).

It should be noted, however, that the magnitude of adjustment, as well as the absolute values in Figs. 4 and 5, may vary from case to case since the measured DLG values can be different based on the measurement settings such as field size, depth, and ion chamber [13], [14]. In the study of Wasbo and Valen [14] with Millennium MLCs, the measured DGL values for 6X increased approximately by 0.1 mm (from 1.7 mm to 1.8 mm) with the measurement depth changed from 5 cm to 15 cm and the field size from 6 × 6 cm² to 14 × 14 cm². Mullins et al. [13] also reported higher measured DLG values when measured with a smaller volume (0.125 cc, 6.5 mm length) ion-chamber, primarily due to the chamber polarity effect. These variations and uncertainties in measuring the physical DLG values support the idea of determining the final DLG values based on a set of clinical plan measurements. However, care must be taken since any source of systematic uncertainties in the plan dose measurements and calculations will induce a systematic uncertainty in the final commissioned system. There are many potential sources of uncertainties, which include, but not limited to, the volume-averaging effect from finite chamber size, chamber calibration, dose calculation grid resolution, and et cetera. Therefore, validating the final DLG values using independent dosimeters such as films and diode arrays is of great importance.

As noted in the introduction section, similar approaches were reported in other papers. The measured and adjusted DLG values of three different treatment units with HD120 MLC are summarized in the Supplementary material Table S6. The measured DLG values in the Wen et al. study [7] were 0.5 mm (6XFFF) and 0.6 mm (10XFFF) on the same machine as that of this study. The DLG of 6X was not presented in the study. They increased the values to 0.7 mm (6XFFF) and 1.0 mm (10XFFF) to reduce plan measurement errors. On the other hand, Kielar et al. [8] delivered a series of step-and-shoot MLC patterns onto films, measured radiation field offset (RFO), and then took twice the value as their measured DLG (0.5 mm) for the energies of 6X, 6XFFF, 10X, 10XFFF, and 15X. Then, the measured value was increased to 1.7 mm to lower their plan measurement errors within 2%. Interestingly, they reported that there was no difference in measured DLG values among different energies, and also their TPS (Eclipse AAA v8.9) allowed only one DLG value for all energies at the time. In regards of the final DLG values, our values were higher than those of Wen et al. study, but lower than that of Kielar et al. study. In addition, Yao and Farr also proposed a method to determine optimal DLG values and tested on four Varian and one Siemens machines [15]. Their method for the Varian machines also used a set of sliding window MLC patterns. However, unlike the conventional approach, the leaves “marched” at the same speed but at difference positions so that the gaps have a certain length of exposed tongues and grooves, denoted as “T&G extension” in the study. In order to determine the optimal DLG values, the measured doses were compared to the TPS doses for a set of MLC patterns with gaps ranging from 5 to 30 mm and T&G extensions ranging from 5 to 20 mm. Their reported optimal DLG for 6X was smaller (0.6 mm) than the values of other studies for a HD120 MLC equipped on a TrueBeam STx machine. No other energy was investigated in the study.

There have been several DLG related publications for Millennium 120 MLCs [9], [15], [16], [17]. As expected, the reported values were larger than those of HD120 MLCs due to more scattering and transmitting radiation through round leaf ends with smaller curvature radius (8 cm) than that of HDMLC (16 cm). Mei and Ian measured DLG values of 1.52 mm, 1.86 mm, and 1.88 mm for 6X on three different C-series treatment units and reported a good agreement between measurements and IMRT dose calculations (Eclipse AAA v8.6, Varian Medical Systems, Palo Alto, CA) [9]. Lee et al. measured a DLG of 2.0 mm from static square MLC fields of size 1–4 cm (Varian 21EX, 6X, Eclipse, Pencil Beam v8.6, Varian Medical Systems, Palo Alto, CA) [17]. Chauvet et al. proposed a method to find a slit width (sweeping gap) first that produces equivalent uniform dose distribution between the planning system and the measured dose, and then to determine the DLG and transmission (T) factor combination that generates such optimal slit width in the planning system [16]. The approach however seems limited from a practical perspective because, as they reported, different (DLG, T) combinations produced the same optimal slit width, and the method may not be applicable for the FFF mode. In the study, the optimal slit width was found to be 6 mm and the (DLG, T) combinations were in the range of (1.7 mm, 1.6%) ∼ (2.0 mm, 1.5%) for 20X photon energy (CL23EX, CadPlan Helios v 6.3.6, Varian Medical Systems, Palo Alto, CA). Yao and Farr [15] reported optimal DLG values as well for three Millennium 120 MLCs; 2.3 mm, 2.3 mm, and 2.5 mm respectively, which were larger than other aforementioned studies.

There are various types of MLCs, and their designs and controls are complex [4]. A number of physical and dosimetry parameters are generally measured to characterize different types of MLCs, which include, but not limited to, the leaf position/alignment accuracy, readout and radiation field congruence, static and dynamic leaf gap, tongue-and-groove effect, asymmetric radiation penumbra, leaf transmission and leakage, and leaf travel speed [6], [18]. Further, the associated controller software may affect the dosimetry properties and delivery accuracy as well [9]. Proper modeling for accurate dose calculation is therefore required to accommodate those variations. However, the AAA photon dose calculation algorithm in Eclipse (version 13.6, Varian Medical System, Palo Alto, CA) requires only two parameters per energy: the dosimetric leaf gap (DLG) and mean transmission factor through the closed leaves. The mean transmission factor takes into account both interleaf leakage and leaf transmission. According to the vendor documentation [Eclipse Photon and Electron Algorithms Reference Guide (version 13.7)], the tongue-and-groove effect is also taken into account, but the groove effect is ignored from a small expected error. There is no associated parameter to enter in TPS for the tongue-and-groove effect. The MLC leaf ends are round in shape for better off-axis dosimetric characteristics. The AAA algorithm models the leaf ends as sharp edges, as opposed to rounded edges, but instead pulls the leaves back to each end by the half of DLG value in order to increase the effective MLC opening. Further, the use of a single DLG value is insufficient since the difference between radiological and nominal leaf position differs at different off-axis leaf position. This simple modeling approach may contribute errors in the calculated dose to some extent. The MLC transmission factor, DLG, and tongue-and-groove effect algorithm all affect the fluence map (Eclipse Photon and Electron Algorithms Reference Guide ver. 13.7), and the final fluence map is used for dose calculation. The smallest fluence map resolution was 1 × 1 mm² when the dose calculation grid resolution was set to 1 mm in Eclipse, which might be another source of error for HD120 MLC with a small 2.5 mm leaf width in contrast to other regular MLCs of 5–10 mm leaf widths. For more details on the dose calculation and source modeling, see a vendor white paper by Torsti et al. [19].

As demonstrated in Figs. 4 and 5, the dose errors were dependent on the MLC sweeping gap size as well as the primary collimator opening (jaw size). In other words, there was no one optimal DLG value for all settings. With a larger DLG value, the overall plan dose increases because of the wider effective MLC opening. Therefore, based on Fig. 4, a larger DLG value will make less errors for plans with larger MLC gaps, but more errors for plans with smaller MLC gaps, and vice versa. For the five spine SBRT plans in this study, the mean gaps were in the range of 14.6 mm and 22.9 mm (Supplementary material Fig. S2). The corresponding maximum measurement error was 1.6% with the final DLG value. Because the machine was mainly for cranial and extra-cranial radiosurgery program in this study, we tuned the DLG values based on the radiosurgery plans using a micro ionization chamber. However, the resultant DLG values also produced good 2D film dose measurement results for spine plans as well as small IC measurement errors for regular IMRT plans. The measurement 95% confident limit (CL = |mean| ± 1.96SD) of AAPM TG119 plans was 2.0%, compared to the median 4.4% CL of ten participating institutions in the TG119 report [12]. It is not presented in this report, but we also measured doses with static rectangular MLC fields of sizes 4 × 4 cm² ∼ 30 × 20 cm². The maximum difference between calculated and measured doses was only 0.6%. Therefore, the method of adjusting the DLG values based on a set of clinical treatment plans is a viable option for determining DLG values. Further, the linearity between DLG and dose error (Fig. 2) may allow one to find the final DLG values via interpolation based on two measurement points.

In summary, the use of physical DLG values, measured by the conventional sweeping gap MLC patterns, produced lower calculated doses than expected. It was necessary to increase the measured DLG values to minimize the discrepancy. The optimal DLG values were also dependent on the plan characteristics, including the MLC gap statistics and jaw sizes. A set of extensive validation work presented in this study is suggestive that determining the DLG values based on a set of clinical treatment plan measurements is a clinically viable method.

Conflict of interest.

None of the authors has conflict of interest.