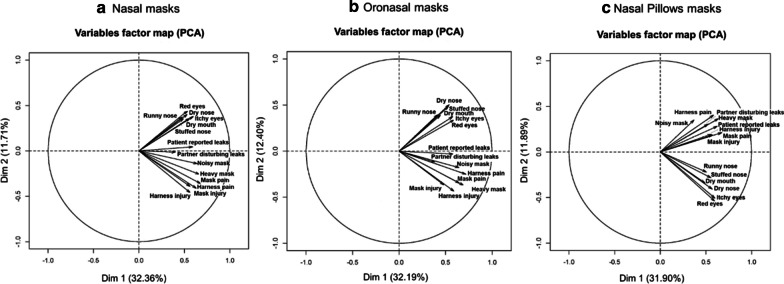
Fig. 3.

Principal Component Analysis (PCA) of the mask related side-effects for a nasal, b oronasal, c nasal pillows masks. Note that PCA is a procedure that transforms possibly correlated variables into a smaller number of uncorrelated variables called principal components. In this process, linear relationships among variables are found (components), with each component being uncorrelated with the others (orthogonal) in directions defined by an eigenvector. The first principal component accounts for as much of the variability in the data as possible, and each succeeding component accounts for as much of the remaining variability as possible (with the restriction of being orthogonal to/independent of the preceding component). Within this framework, the reader should understand that two arrows pointing in the same direction and close to each other are positively correlated, two arrows pointing in opposite directions are negatively correlated, and arrows at right angles are independent. Here, the three plots present a similar explained total variance for PC1 of 31.90% to 32.36%, PC2 of only 11.7% to 12.4% and only minor differences in positioning of the vectors for each MRSE on the 3 plots. In consequence, PCA analyses suggest few differences for MRSE associations between mask types. Independently of the mask-type, two groups of eigenvectors can be described. The first group is composed of red eyes, itchy eyes, dry nose, runny nose, stuffed nose and dry mouth eigenvectors (PCA group-1). The second group is composed of mask pain, harness pain, mask injury, harness injury, heavy mask, patient reported leaks, partner disturbing leaks and noisy mask eigenvectors (PCA group-2). These two groups are independent between them whereas their constitutive MRSE variables are associated. For nasal pillow masks, the group-2 composition is similar but with an increased association between constitutive MRSE variables