FairALM: Augmented Lagrangian Method for Training Fair Models with Little Regret

Abstract

Algorithmic decision making based on computer vision and machine learning methods continues to permeate our lives. But issues related to biases of these models and the extent to which they treat certain segments of the population unfairly, have led to legitimate concerns. There is agreement that because of biases in the datasets we present to the models, a fairness-oblivious training will lead to unfair models. An interesting topic is the study of mechanisms via which the de novo design or training of the model can be informed by fairness measures. Here, we study strategies to impose fairness concurrently while training the model. While many fairness based approaches in vision rely on training adversarial modules together with the primary classification/regression task, in an effort to remove the influence of the protected attribute or variable, we show how ideas based on well-known optimization concepts can provide a simpler alternative. In our proposal, imposing fairness just requires specifying the protected attribute and utilizing our routine. We provide a detailed technical analysis and present experiments demonstrating that various fairness measures can be reliably imposed on a number of training tasks in vision in a manner that is interpretable.

1. Introduction

Fairness and non-discrimination is a core tenet of modern society. Driven by advances in vision and machine learning systems, algorithmic decision making continues to permeate our lives in important ways. Consequently, ensuring that the decisions taken by an algorithm do not exhibit serious biases is no longer a hypothetical topic, rather a key concern that has started informing legislation [23] (e.g., Algorithmic Accountability act). On one extreme, some types of biases can create inconvenience – a biometric access system could be more errorprone for faces of persons from certain skin tones [9] or a search for homemaker or programmer may return gender-stereotyped images [8]. But there are serious ramifications as well – an individual may get pulled aside for an intrusive check while traveling [50] or a model may decide to pass on an individual for a job interview after digesting their social media content[13,25]. Biases in automated systems in estimating recidivism within the criminal judiciary have been reported [38]. There is a growing realization that these problems need to be identified and diagnosed, and then promptly addressed. In the worst case, if no solutions are forthcoming, we must step back and reconsider the trade-off between the benefits versus the harm of deploying such systems, on a case by case basis.

What leads to unfair learning models?

One finds that learning methods in general tend to amplify biases that exist in the training set [46]. While this creates an incentive for the organization training the model to curate datasets that are “balanced” in some sense, from a practical standpoint, it is often difficult to collect data that is balanced along multiple “protected” variables, e.g., gender, race and age. If a protected feature is correlated with the response variable, a learning model can cheat and find representations from other features that are collinear or a good surrogate for the protected variable. A thrust in current research is devoted to devising ways to mitigate such shortcuts. If one does not have access to the underlying algorithm, a recent result [24] shows the feasibility of finding thresholds that can impose certain fairness criteria. Such a threshold search can be post-hoc applied to any learned model. But in various cases, because of the characteristics of the dataset, a fairness-oblivious training will lead to biased models. An interesting topic is the study of mechanisms via which the de novo design/training of the model can be informed by fairness measures.

Some general strategies for Fair Learning.

Motivated by the foregoing issues, recent work which may broadly fall under the topic of algorithmic fairness has suggested several concepts or measures of fairness that can be incorporated within the learning model. While we will discuss the details shortly, these include demographic parity [40], equal odds and equal opportunities [24], and disparate treatment [42]. In general, existing work can be categorized into a few distinct categories. The first category of methods attempts to modify the representations of the data to ensure fairness. While different methods approach this question in different ways, the general workflow involves imposing fairness before a subsequent use of standard machine learning methods [10,27]. The second group of methods adjusts the decision boundary of an already trained classifier towards making it fair as a post-processing step while trying to incur as little deterioration in overall performance as possible [22,21,39]. While this procedure is convenient and fast, it is not always guaranteed to lead to a fair model without sacrificing accuracy. Part of the reason is that the search space for a fair solution in the post-hoc tuning is limited. Of course, we may impose fairness during training directly as adopted in the third category of papers such as [43,4], and the approach we take here. Indeed, if we are training the model from scratch and have knowledge of the protected variables, there is little reason not to incorporate this information directly during model training. In principle, this strategy provides the maximum control over the model. From the formulation standpoint, it is slightly more involved because it requires satisfying a fairness constraint derived from one or more fairness measure(s) in the literature, while concurrently learning the model parameters. The difficulty varies depending both on the primary task (shallow versus deep model) as well as the specific fairness criteria. For instance, if one were using a deep network for classification, we would need to devise ways to enforce constraints on the output of the network, efficiently.

Scope of this paper and contributions.

Many studies on fairness in learning and vision are somewhat recent and were partly motivated in response to more than a few controversial reports in the news media [17,31]. As a result, the literature on mathematically sound and practically sensible fairness measures that can still be incorporated while training a model is still in a nascent stage. In vision, current approaches have largely relied on training adversarial modules in conjunction with the primary classification or regression task, to remove the influence of the protected attribute. Adversarial training via SGD needs a great deal of care and is not straightforward [36]. In contrast, the contribution of our work is to provide a simpler alternative. We show that a number of fairness measures in the literature can be incorporated by viewing them as constraints on the output of the learning model. This view allows adapting ideas from constrained optimization, to devise ways in which training can be efficiently performed in a way that at termination, the model parameters correspond to a fair model. For a practitioner, this means that no changes in the architecture or model are needed: imposing fairness only requires specifying the protected attribute, and utilizing our proposed optimization routine.

2. A Primer on Fairness Functions

In this section, we introduce basic notations and briefly review several fairness measures described in the literature.

Basic notations.

We denote classifiers using h : x ↦ y where x and y are random variables that represent the features and labels respectively. A protected attribute is a random variable s on the same probability space as x and y – for example, s may be gender, age, or race. Collectively, a training example would be z ≔ (x, y, s). So, our goal is to learn h (predict y given x) while imposing fairness-type constraints over s. We will use $\mathcal{H}=\left\{h_1,h_2,\dots ,h_N\right\}$ to denote a set/family of possible classifiers and Δ^N to denote the probability simplex in ${ℝ}^N$, i.e., $\Delta ≔\left\{q:{\sum }_{i=1}^N{q}_i=1,q_i\ge 0\right\}$ where q_i is the i-th coordinate of q.

We will assume that the distribution of s has finite support. Unless explicitly specified, we will assume that y ∈ {0, 1}. For each $h\in \mathcal{H}$, we will use e_h to denote the misclassification rate of h and $e_{\mathcal{H}}\in {ℝ}^N$ to be the vector containing all misclassification rates. We will use superscript to denote conditional expectations. That is, if μ_h corresponds to expectation of some function μ (that depends on $h\in \mathcal{H}$), then the conditional expectation/moment of μ_h with respect to s will be denoted by ${\mu }_h^s$. With a slight abuse of notation, we will use ${\mu }_h^{s_0}$ to denote the elementary conditional expectation μ_h|(s = s₀) whenever it is clear from context. We will use d_h to denote the difference between the conditional expectation of the two groups of s, that is, $d_h≔{\mu }_h^{s_0}-{\mu }_h^{s_1}$. For example, let s be the random variable representing gender, that is, s₀ and s₁ may correspond to male and female. Then, $e_h^{s_i}$ corresponds to the misclassification rate of h on group s_i, and $d_h=e_h^{s_0}-e_h^{s_1}$. Finally, ${\mu }_h^{s_{i,}{t}_j}≔{\mu }_h\mid (s=s_i,t=t_j)$ denotes the elementary conditional expectation with respect to two random variables s, t.

2.1. Fairness through the lens of Confusion Matrix

Recall that a fairness constraint corresponds to a performance requirement of a classifier h on subgroups of features x induced by a protected attribute s. For instance, say that h predicts the credit-worthiness y of an individual x. Then, we may require that e_h be “approximately” the same across individuals for different races given by s. Does it follow that functions/metrics that are used to evaluate fairness may be written in terms of the error of a classifier e_h conditioned on the protected variable s (or in other words $e_h^s$)? Indeed, it does turn out to be the case. In fact, many widely used functions in practice can be viewed as imposing constraints on the confusion matrix as our intuition suggests. We will now discuss few common fairness metrics to illustrate this idea.

1. Demographic Parity (DP) [40]. A classifier h is said to satisfy Demographic Parity (DP) if h(x) is independent of the protected attribute s. Equivalently, h satisfies DP if d_h = 0 where we set ${\mu }_h^{s_i}=e_h^{s_i}$ (using notations introduced above). DP can be seen as equating the total false positives and false negatives between the confusion matrices of the two groups. We denote DDP by the difference of the demographic parity between the two groups.

2. Equality of Opportunity (EO) [24]. A classifier h is said to satisfy EO if h(x) is independent of the protected attribute s for y ∈ {0, 1}. Equivalently, h satisfies EO if $d_h^y=0$ where we set ${\mu }_h^{s_i}=e_h^{s_i}\mid (y\in \left\{0,1\right\})≕e_h^{s_i,y_j}$ conditioning on both s and y. Depending on the choice of y in ${\mu }_h^{s_i}$, we get two different metrics: (i) y = 0 corresponds to h with equal False Positive Rate (FPR) across s_i [14], whereas (ii) y = 1 corresponds to h with equal False Negative Rate (FNR) across s_i [14]. Moreover, h satisfies Equality of Odds if $d_h^0+d_h^1=0$, i.e., h equalizes both TPR and FPR across s [24]. We denote the difference in EO by DEO.

3. Predictive Parity (PP) [11]. A classifier h satisfies PP if the likelihood of making a misclassification among the positive predictions of the classifier is independent of the protected variable s. Equivalently, h satisfies PP if $d_h^{\widehat{y}}=0$ where we set ${\mu }_{h_i}^{s_i}=e_h^{s_i}\mid (\widehat{y}=1)$. It corresponds to matching the False Discovery Rate between the confusion matrices of the two groups.

3. How to learn fair models?

At a high level, the optimization problem that we seek to solve is written as,

$$\underset{h\in \mathcal{H}}{\text{min }}{\mathbb{E}}_{z:(x,y,s)~\mathcal{D}}\mathcal{L}(h;(x,y))\text{ subject to }h\in {\mathcal{F}}_{d_h},$$ (1)

where $\mathcal{L}$ denotes the loss function that measures the accuracy of h in predicting y from x, and ${\mathcal{F}}_{d_h}$ denotes the set of fair classifiers. Our approach to solve (1) provably efficiently involves two main steps: (i) first, we reformulate problem (1) to compute a posterior distribution q over $\mathcal{H}$; (ii) second, we incorporate fairness as soft constraints on the output of q using the augmented Lagrangian of Problem (1). We assume that we have access to sufficient number of samples to approximate $\mathcal{D}$ and solve the empirical version of Problem (1).

3.1. From Fair Classifiers to Fair Posteriors

The starting point of our development is based on the following simple result that follows directly from the definitions of fairness metrics in Section 2:

Observation 1. Fairness metrics such as DP/EO are linear functions of h, whereas PP takes a linear fractional form due to the conditioning on $\widehat{y}$, see [11].

Observation 1 immediately implies that ${\mathcal{F}}_{d_h}$ can be represented using linear (fractional) equations in h. To simplify the discussion, we will focus on the case when ${\mathcal{F}}_{d_h}$ is given by the DP metric. Hence, we can reformulate (1) as,

$$\underset{q\in \Delta }{\text{min}}\sum _i{q}_i{e}_{h_i}\text{ s.t. }{q}_i\left({\mu }_{h_i}^{s_0}-{\mu }_{h_i}^{s_1}\right)=0\forall i\in [N],$$ (2)

where q represents a distribution over $\mathcal{H}$.

3.2. Imposing Fairness via Soft Constraints

In general, there are two ways of treating the N constraints $q_i{d}_{h_i}=0$ in Problem (2) viz., (i) as hard constraints; or (ii) as soft constraints. Algorithms that can handle explicit constraints efficiently require access to an efficient oracle that can minimize a linear or quadratic function over the feasible set in each iteration. Consequently, algorithms that incorporate hard constraints come with high periteration computational cost since the number of constraints is (at least) linear in N, and is not applicable in large scale settings. Hence, we propose to use algorithms that incorporate fairness as soft constraints. With these two minor modifications, we will now describe our approach to solve problem (2).

4. Fair Posterior from Proximal Dual

Following the reductions approach in [1], we first write the Lagrangian dual of DP constrained risk minimization problem (2) using dual variables λ as,

$$\underset{\lambda \in {ℝ}^N}{\text{max }}\underset{q\in \Delta }{\text{min }}L(q,\lambda )≔\left(\sum _i{q}_i{e}_{h_i}\right)+\lambda \left(\sum _i{q}_i\left({\mu }_{h_i}^{s_0}-{\mu }_{h_i}^{s_1}\right)\right)$$ (3)

Interpreting the Lagrangian.

Problem 3 can be understood as a game between two players: a q-player and a λ-player [16]. We recall an important fact regarding the dual problem (3):

Fact 2. The objective function of the dual problem (3) is always nonsmooth with respect to λ because of the inner minimization problem in q.

Technically, there are two main reasons why optimizing nonsmooth functions can be challenging [19]: (i) finding a descent direction in high dimensions N can be difficult; and (ii) subgradient methods can be slow to converge in practice. Due to these difficulties arising from Fact 2, using a first order algorithm such as gradient descent to solve the dual problem in (3) directly can be problematic, and may be suboptimal.

Accelerated optimization using Dual Proximal Functions.

To overcome the difficulties due to the nonsmoothness of the dual problem, we propose to augment the Lagrangian with a proximal term. Specifically, for some λ_T, the augmented Lagrangian function can be written as,

$$L_T(q,\lambda )=\left(\sum _i{q}_i{e}_{h_i}\right)+\lambda \left(\sum _i{q}_i\left({\mu }_{h_i}^{s_0}-{\mu }_{h_i}^{s_1}\right)\right)-\frac{1}{2\eta }{\left(\lambda -{\lambda }_T\right)}^2$$ (4)

Note that, as per our simplified notation, $L_T\equiv L_{{\lambda }_T}$. The following lemma relates the standard Lagrangian in (3) with its proximal counterpart in (4).

Lemma 1. At the optimal solution (q*, λ*) to L, we have max_λ min_q∈Δ L = max_λ min_q∈_Δ L_λ*.

This is a standard property of proximal objective functions, where λ* forms a fixed point of min_q∈Δ L_λ*(q, λ*) (section 2.3 of [32]). Intuitively, Lemma 1 states that L and L_T are not at all different for optimization purposes.

Remark 1. While the augmented Lagrangian L_T still may be nonsmooth, the proximal (quadratic) term can be exploited to design provably faster optimization algorithms as we will see shortly.

5. Our Algorithm – FairALM

It is common [1,16,28] to consider the minimax problem in (4) as a zero sum game between the λ-player and the q-player. The Lagrangian(s) L_T (or L) specify the cost which the q-player pays to the λ-player after the latter makes its choice. We update the λ-player by follow-the-leader method [37] which minimizes the cumulative regret. This is distinct from a dual ascent method which relies on a gradient based update scheme. Further, the q-player is updated by following a best response strategy as in [1]. While the q-player’s move relies on the availability of an efficient oracle to solve the minimization problem, L_T(q, λ), being a linear program in q makes it less challenging. We describe our algorithm in Alg. 1 and call it FairALM: Linear Classifier.

5.1. Convergence Analysis

As the game with respect to λ is a maximization problem, we get a reverse regret bound as shown in the following Lemma. Proofs are deferred to the appendix.

Lemma 2. Let r_t denote the reward at each round of the game. The reward function f_t(λ) is defined as $f_t(\lambda )=\lambda r_t-\frac{1}{2\eta }{\left(\lambda -{\lambda }_t\right)}^2$. We choose λ in round T + 1 to maximize the cumulative reward: ${\lambda }_{T+1}={\text{argmax}}_{\lambda }{\sum }_{t=1}^T{f}_t(\lambda )$. Define L = max_t |r_t|. The following bound on the cumulative reward holds, for any λ

$$\sum _{t=1}^T\left(\lambda r_t-\frac{1}{2\eta }{\left(\lambda -{\lambda }_t\right)}^2\right)\le \sum _{t=1}^T{\lambda }_t{r}_t+\eta L^2\mathcal{O}(\text{log }T)$$ (5)

The above lemma indicates that the cumulative reward grows in time as $\mathcal{O}(\text{log }T)$. The proximal term in the augmented Lagrangian gives us a better bound than an ℓ₂ or an entropic regularizer (which provides a $\sqrt{T}$ bound [37]).

Next, we evaluate the cost function L_T(q, λ) after T rounds of the game. We observe that the average play of both the players converges to a saddle point with respect to L_T(q, λ). We formalize this in the following theorem,

Theorem 3. Recall that d_h represents the difference of conditional means. Assume that ∥d_h∥_∞ ≤ L and consider T rounds of the game described above. Let the average plays of the q-player be $\overline{q}=\frac{1}{T}{\sum }_{t=1}^T{q}_t$ and the λ-player be $\overline{\lambda }=\frac{1}{T}{\sum }_{t=1}^T{\lambda }_t$. Then under the following conditions on q, λ and η, we have $L_T(\overline{q},\overline{\lambda })\le L_T(q,\overline{\lambda })+\nu$ and $L_T(\overline{q},\overline{\lambda })\ge L_T(\overline{q},\lambda )-\nu$

• If $\eta =\mathcal{O}(\sqrt{\frac{B^{2}T}{L^2(\text{log }T+1)})}$, $\nu =\mathcal{O}\left(\sqrt{\frac{B^2{L}^2(\text{log }T+1)}{T}}\right)$; ∀|λ|≤ B, ∀q ∈ Δ

• If $\eta =\frac{1}{T}$, $\nu =\mathcal{O}\left(\frac{L^2{(\text{log }T+1)}^2}{T}\right)$; $\forall \lambda \in ℝ$, ∀q ∈ Δ

The above theorem indicates that the average play of the q-player and the λ-player reaches a ν-approximate saddle point. Our bounds for $\nu =\frac{1}{T}$ and $\lambda \in ℝ$ are better than [1].

Algorithm 1.

FairALM: Linear Classifier

1: Notations: Dual step size η

ht ∈ {h1, h2,…, hN }.

2: Input: Error Vector $e_{\mathcal{H}}$,

Conditional mean vector ${\mu }_{\mathcal{H}}^s$

3: Initializations: λ0 = 0

4: for t = 0,1, 2, …, T do

5:  (Primal) $h_t\leftarrow {\text{argmin}}_i\left(e_{h_i}+{\lambda }_t\left({\mu }_{h_i}^{s_0}-{\mu }_{h_i}^{s_1}\right)\right)$

6:   (Dual) ${\lambda }_{t+1}\leftarrow {\lambda }_t+\eta \left({\mu }_{h_t}^{s_0}-{\mu }_{h_t}^{s_1}\right)/t$

7: end for

8: Output: hT

Algorithm 2.

FairALM: DeepNet Classifier

1: Notations: Dual step size η, Primal step size τ

2: Input: Training Set D

3: Initializations: λ0 = 0, w0

4: for t = 0, 1, 2, …, T do

5:  Sample z ~ D

6:  Pick $v_t\in \partial \left({\widehat{e}}_{h_w}(z)+\left({\lambda }_t+\eta \right){\widehat{\mu }}_{h_w}^{s_0}(z)-\left({\lambda }_t-\eta \right){\widehat{\mu }}_{h_w}^{s_1}(z)\right)$

7:   (Primal) wt ← wt−1 – τvt

8:   (Dual) ${\lambda }_{t+1}\leftarrow {\lambda }_t+\eta \left({\widehat{\mu }}_{h_{w_t}}^{s_0}(z)-{\widehat{\mu }}_{h_{w_t}}^{s_1}(z)\right)$

9: end for

10: Output: wT

5.2. Can we train Fair Deep Neural Networks by adapting Alg. 1?

The key difficulty from the analysis standpoint we face in extending these results to the deep networks setting is that the number of classifiers $\left|\mathcal{H}\right|$ may be exponential in number of nodes/layers. This creates a potential problem in computing Step 5 of Algorithm 1 – if viewed mechanistically, it is not practical since an epsilon net over the family $\mathcal{H}$ (representable by a neural network) is exponential in size. Interestingly, notice that we often use over-parameterized networks for learning. This is a useful fact here because it means that there exists a solution where ${\text{argmin}}_i\left(e_{h_i}+{\lambda }_t{d}_{h_i}\right)$ is 0. While iterating through all h_is will be intractable, we may still able to obtain a solution via standard stochastic gradient descent (SGD) procedures [45]. The only unresolved question then is if we can do posterior inference and obtain classifiers that are “fair”. It turns out that the above procedure provides us an approximation if we leverage two facts: first, SGD can find the minimum of L(h, λ) with respect to h and second, recent results show that SGD, in fact, performs variational inference, implying that the optimization can provide an approximate posterior [12]. Having discussed the the exponential sized $\left|\mathcal{H}\right|$ issue – for which we settle for an approximate posterior – we make three additional adjustments to the algorithm to make it suitable for training deep networks. First, the non-differentiable indicator function $\mathbb{1}[\cdot ]$ is replaced with a smooth surrogate function (such as a logistic function). Second, as it is hard to evaluate $e_h/{\mu }_h^s$ due to unavailability of the true data distribution, we instead calculate their empirical estimates z = (x; y; s), and denote it by ${\widehat{e}}_h(z)/{\widehat{\mu }}_h^s(z)$. Third, by exchanging the “max” and “min” in (3), we obtain an objective that upper-bounds our current objective in (3). This provides us with a closed-form solution to λ thus reducing the minmax objective to a single simpler minimization problem. We present our FairALM: DeepNet Classifier algorithm for deep neural network training in Alg. 2 (more details are in the supplement).

6. Experiments

A central theme in our experiments is to assess whether our proposed algorithm, FairALM, can indeed obtain meaningful fairness measure scores without compromising the test set performance. We evaluate FairALM on a number of problems where the dataset reflects certain inherent societal/stereotypical biases. Our evaluations are also designed with a few additional goals in mind.

Overview.

Our first experiment on the CelebA dataset seeks to predict the value of a label for a face image while controlling for certain protected attributes (gender, age). We discuss how prediction of some labels is unfair in an unconstrained model and contrast with our FairALM. Next, we focus on the label where predictions are the most unfair and present comparisons against methods available in the literature. For our second experiment, we use the ImSitu dataset where images correspond to a situation (activities, verb). Expectedly, some activities such as driving or cooking are more strongly associated with a specific gender. We inspect if an unconstrained model is unfair when we ask it to learn to predict two gender correlated activities/verbs. Comparisons with baseline methods will help measure FairALM’s strengths/weaknesses. We can use heat map visualizations to qualitatively interpret the value of adding fairness constraints. We threshold the heat-maps to get an understanding of a general behavior of the models. Our third experiment addresses an important problem in medical/scientific studies. Small sample sizes necessitate pooling data from multiple sites or scanners [49], but introduce a site or scanner specific nuisance variable which must be controlled for – else a deep (also, shallow) model may cheat and use site specific (rather than disease-specific) artifacts in the images for prediction even when the cohorts are age or gender matched [20]. We study one simple setting here: we use FairALM to mitigate site (hospital) specific differences in predicting “tuberculosis” from X-ray images acquired at two hospitals, Shenzhen and Montgomery (and recently made publicly available [26]).

In all the experiments, we impose Difference in Equality of Opportunity (DEO) constraint (defined in Section 2.1). We adopt NVP (novel validation procedure) [18] a two-step procedure: first, we search for the hyper-parameters that achieve the best accuracy, and then, we report the minimum fairness measure (DEO) for accuracies within 90% of the highest accuracy.

Remark.

Certain attributes such as attractiveness, obtained via crowd-sourcing, may have socio-cultural ramifications. Similarly, the gender attribute in the dataset is binary (male versus female) which may be insensitive. We clarify that our goal is to present evidence showing that our algorithm can impose fairness in a sensible way on datasets used in the literature and acknowledge that larger/improved datasets focused on societally relevant themes, as they become available, will be much more meaningful.

6.1. CelebA dataset

Data and Setup.

CelebA [29] consists of 200K celebrity face images from the internet annotated by a group of paid adult participants [7]. There are up to 40 labels available in the dataset, each of which is binary-valued.

Quantitative results.

We begin our analysis by predicting each of the 40 labels with a 3-layer ReLU network. The protected variable, s, we consider are the binary attributes like Male and Young representing gender and age respectively. We train the SGD algorithm for 5-epochs and select the labels predicted with at least at 70% precision and with a DEO of at least 4% across the protected variables. The biased set of labels thus estimated are shown in Fig 1. These labels are consistent with other reported results [34]. It is important to bear in mind that the bias in the labels should not be attributed to its relatedness to a specific protected attributed alone. The cause of bias could also be due to the skew in the label distributions. When training a 3-layer ReLU net with FairALM, the precision of the model remained about the same (±5%) while the DEO measure reduced significantly, see Fig 1. Next, choosing the most unfair label in Fig 1 (i.e., attractiveness), we train a ResNet18 for a longer duration of about 100 epochs and contrast the performance with a simple ℓ₂-penalty baseline. The training profile is observed to be more stable for FairALM as indicated in Fig 2. This finding is consistent with the results of [5,30] that discuss the ill-conditioned landscape of non-convex penalties. Comparisons to more recent works such as [35,33] is provided in Fig 2. Here, we present a new state-of-the-art result for the DEO measure with the label attractiveness and protected attribute gender.

Fig.1: Identifying Unfair Labels in CelebA dataset.

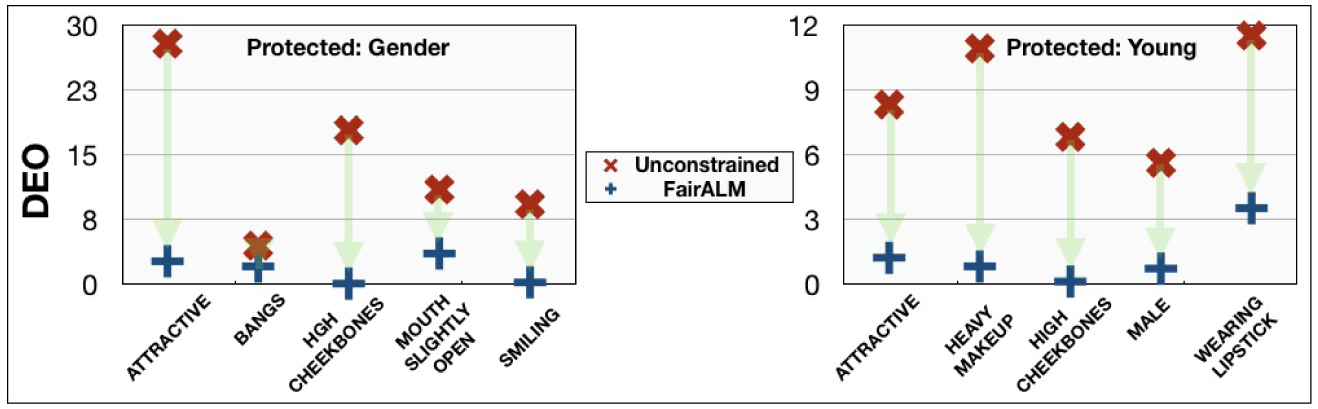
Using a 3-layers ReLU network, we determine the labels in CelebA dataset that are biased with respect to gender (left) and the attribute young (right). FairALM minimizes the DEO measure, indicated by the green arrow, on these labels while maintaining ±5% precision.

Fig.2: Quantitative Results on CelebA.

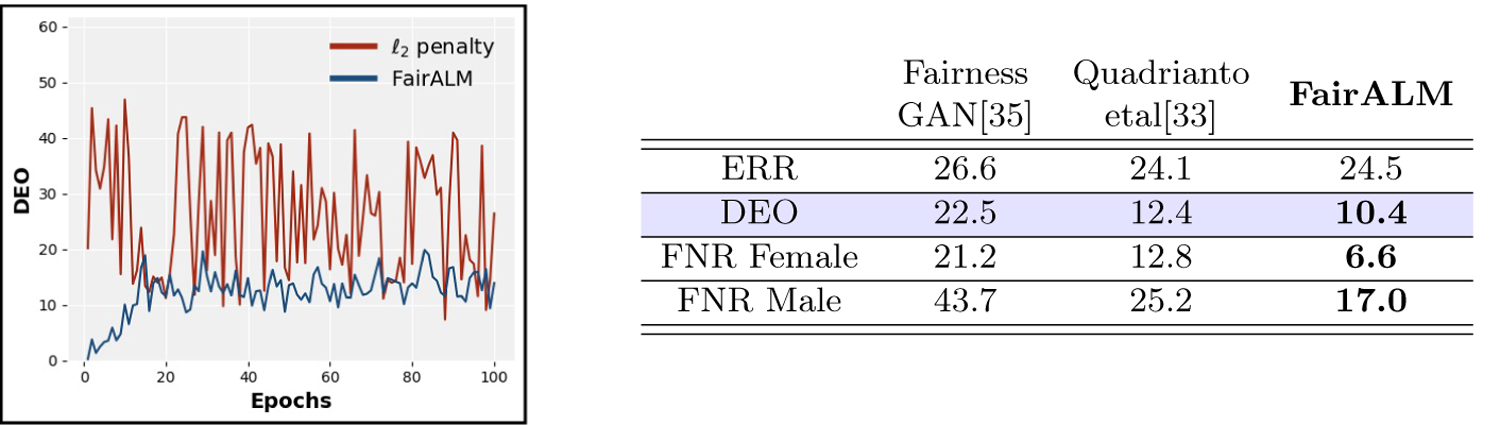
The target attribute is the label attractiveness present in the CelebA dataset and the protected attribute is gender. (left) FairALM has a stable training profile in comparison to naive ℓ₂ penalty. (right) FairALM attains a lower DEO measure and improves the test set errors (ERR).

Qualitatively assessing Interpretability.

While the DEO measure obtained by FairALM is lower, we can ask an interesting question: when we impose the fairness constraint, precisely which aspects of the image are no longer “legal” for the neural network to utilize? This issue can be approached via visualizing activation maps from models such as CAM [48]. As a representative example, our analysis suggests that in general, an unconstrained model uses the entire face image (including the gender-revealing parts). We find some consistency between the activation maps for the label attractiveness and activation maps of an unconstrained model trained to predict gender! In contrast, when we impose the fairness constraint, the corresponding activation maps turn out to be clustered around specific regions of the face which are not gender revealing. In particular, a surprising finding was that the left regions in the face were far more prominent which turns out to be consistent with studies in psychology [6].

Summary.

FairALM minimized the DEO measure without compromising the test error. It has a more stable training profile than an ℓ₂ penalty and is competitive with recent fairness methods in vision. The activation maps in FairALM focus on non-gender revealing features of the face when controlled for gender.

6.2. Imsitu Dataset

Data and Setup.

ImSitu [41] is a situation recognition dataset consisting of ~ 100K color images taken from the web. The annotations for the image is provided as a summary of the activity in the image and includes a verb describing it, the interacting agents and their roles. The protected variable in this experiment is gender. Our objective is to classify a pair of verbs associated with an image. The pair is chosen such that if one of the verbs is biased towards males then the other would be biased towards females. The authors in [47] report the list of labels in the ImSitu dataset that are gender biased: we choose our verb pairs from this list. In particular, we consider the verbs Cooking vs Driving, Shaving vs Moisturizing, Washing vs Saluting and Assembling vs Hanging. We compare our results against multiple baselines such as (1) Unconstrained (2) ℓ₂-penalty, the penalty applied on the DEO measure (3) Re-weighting, a weighted loss functions where the weights account for the dataset skew (4) Adversarial [44] (5) Lagrangian [47] (6) Proxy-Lagrangian [15]. The supplement includes more details on the baseline methods.

Quantitative results.

From Fig 5, it can be seen that FairALM reaches a zero DEO measure very early in training and attains better test errors than an unconstrained model. Within the family of Lagrangian methods such as [47,15], FairALM performs better on verb pair ‘Shaving vs Moisturizing’ in both test error and DEO measure as indicated in Table 1. While the results on the other verb pairs are comparable, FairALM was observed to be more stable to different hyper-parameter choices. This finding is in accord with recent studies by [2] who prove that proximal function models are robust to step-size selection. Detailed analysis is provided in the supplement. Turning now to an adversarial method such as [47], results in Table 1 show that the DEO measure is not controlled as competently as FairALM. Moreover, complicated training routines and unreliable convergence [3,36] makes model-training harder.

Fig.5: Training Profiles.

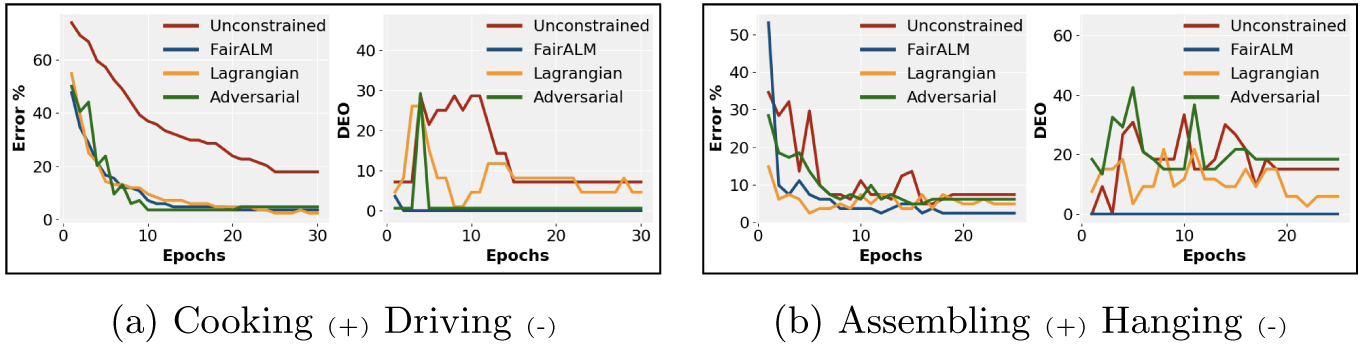
FairALM achieves minimum DEO early in training and remains competitive on testset errors. More plots are available in the supplement.

Table 1: Quantitative Results on ImSitu.

Test errors (ERR) and DEO measure are reported in %. The target class that is to be predicted is indicated by a +. FairALM always achieves a zero DEO while remaining competitive in ERR with the best method for a given verb-pair.

	Cooking(+) Driving(−)		Shaving(+) Moisturize(−)		Washing(+) Saluting(−)		Assembling(+) Hanging(−)
	ERR	DEO	ERR	DEO	ERR	DEO	ERR	DEO
No Constraints	17.9	7.1	23.6	4.2	12.8	25.9	7.5	15.0
ℓ2 Penalty	14.3	14.0	23.6	1.3	10.9	0.0	5.0	21.6
Reweight	11.9	3.5	19.0	5.3	10.9	0.0	4.9	9.0
Adversarial	4.8	0.0	13.5	11.9	14.6	25.9	6.2	18.3
Lagrangian	2.4	3.5	12.4	12.0	3.7	0.0	5.0	5.8
Proxy-lagrangian	2.4	3.5	12.4	12.0	3.7	0.0	14.9	3.0
FairALM	3.6	0.0	20.0	0.0	7.3	0.0	2.5	0.0

Interpretable Models.

We again used CAM [48] to inspect the image regions used by the model for target prediction. We observe that the unconstrained model ends up picking features from locations that may not be relevant for the task description but merely co-occur with the verbs in this particular dataset (and are gender-biased). Fig 4 highlights this observation for the selected classification tasks. Overall, we observe that the semantic regions used by the constrained model are more aligned with the action verb present in the image, and this adds to the qualitative advantages of the model trained using FairALM in terms of interpretability.

Fig.4: Interpretability in ImSitu.

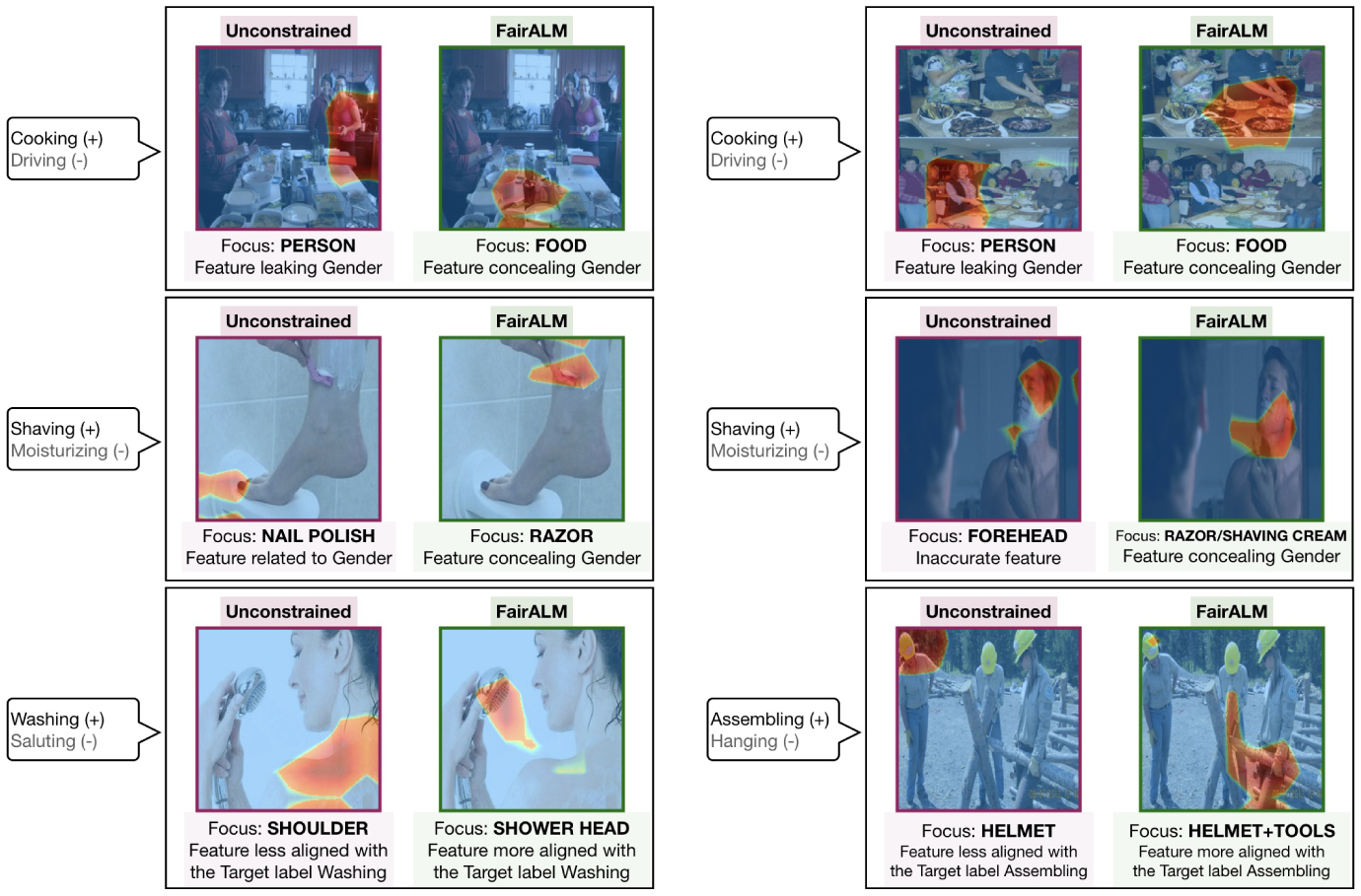
The activation maps indicate that FairALM conceals gender revealing attributes in an image. Moreover, the attributes are more aligned with label of interest. The target class predicted is indicated by a +. These examples are representative of the general behavior of FairALM on this dataset. More plots in the supplement.

Limitations.

We also note that there are cases where both the unconstrained model and FairALM look at incorrect image regions for prediction, owing to the small dataset sizes. However, the number of such cases are far fewer for FairALM than the unconstrained setup.

Summary.

FairALM successfully minimizes the fairness measure while classifying verb/action pairs associated with an image. FairALM uses regions in an image that are more relevant to the target class and less gender revealing.

7. Pooling multi-site chest X-Ray datasets

Data and Setup.

The datasets we examine here are publicly available from the U.S. National Library of Medicine [26]. The images come from two sites/sources - first set is collected from patients in Montgomery county, USA and includes 138 X-rays and the second set of 662 images is collected from a hospital in Shenzhen, China. The task is to predict pulmonary tuberculosis (TB) from the X-ray images. Being collected from different X-ray machines with different characteristics, and the images have site-specific markings or artifacts, see Fig 6. We pool the dataset and set aside 25% of the samples for testing.

Fig.6: Datasets Pooling with FairALM.

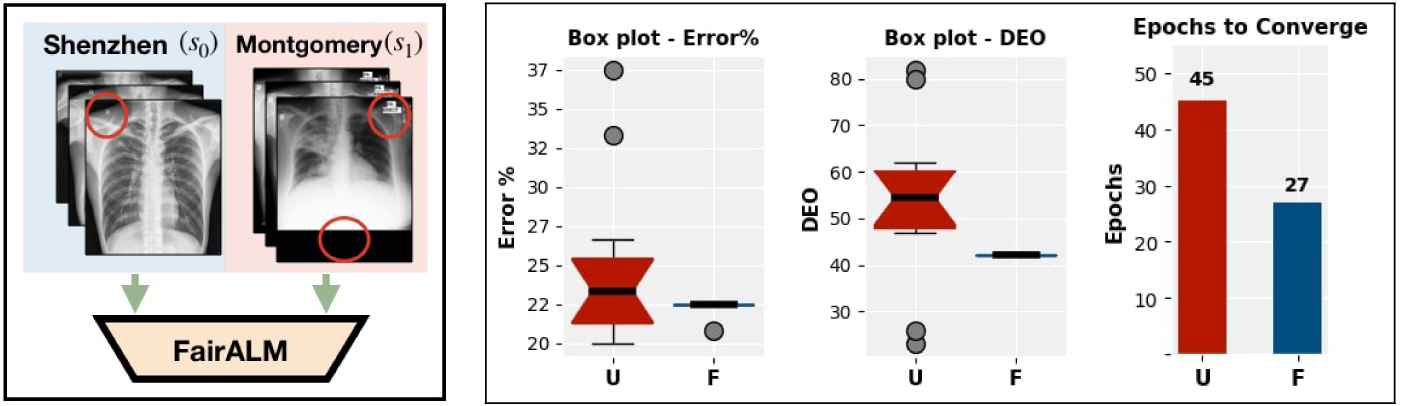
(left:) Data is pooled from two sites/hospitals, Shenzhen s₀ and Montgomery s₁. (right:) Boxplots indicate a lower variance in testset error and the DEO measure for FairALM. Moreover, FairALM reaches a 20% testset error in fewer epochs.

Quantitative Results.

We treat the site information, Montgomery or Shenzhen, as a nuisance/protected variable and seek to decorrelate it from the TB labels. We train a ResNet18 network and compare an unconstrained model with FairALM model. Our datasets of choice are small in size, and so deep models easily overfit to site-specific biases present in the training data. Our results corroborate this conjecture, the training accuracies reach 100% very early and the test set accuracies for the unconstrained model has a large variance over multiple experimental runs. Conversely, as seen in Fig. 6, a FairALM model not only maintains a lower variance in the test set errors and DEO measure but also attains improved performance on these measures. What stands out in this experiment is that the number of epochs to reach a certain test set error is lower for FairALM indicating that the model generalizes faster compared to an unconstrained model.

Summary.

FairALM is effective at learning from datasets from two different sites/sources and minimizes site-specific biases.

8. Conclusion

We introduced FairALM, an augmented Lagrangian framework to impose constraints on fairness measures studied in the literature. On the theoretical side, we provide better bounds: $\mathcal{O}\left(\frac{{\text{log}}^{2}T}{T}\right)$ versus $\mathcal{O}\left(\frac{1}{\sqrt{T}}\right)$, for reaching a saddle point. On the application side, we provide extensive evidence (qualitative and quantitative) on image datasets commonly used in vision to show the benefits of our proposal. Finally, we use FairALM to mitigate site specific differences when performing analysis of pooled medical imaging datasets. In applying deep learning to scientific problems, this is important since sample sizes at individual sites/institutions are often smaller [49]. The overall procedure is simple which we believe will help adoption and follow-up work on this socially relevant topic. The project page is at https://github.com/lokhande-vishnu/FairALM.

Fig.3: Interpretable Models for CelebA.

Unconstrained/FairALM predict the label attractiveness present in the CelebA dataset while controlling gender. The heatmaps of Unconstrained model overlaps with gender classification task indicating gender leak. FairALM consistently picks non-gender revealing features of the face. Interestingly, these regions are on the left side which appear to agree with psychological studies suggesting that a face’s left side is more attractive [6].