Abstract
By analyzing the trajectories of ionized constituents of the lunar exosphere in time-varying electromagnetic fields, we can place constraints on the composition, structure, and dynamics of the lunar exosphere. Heavy ions travel slower than light ions in the same fields, so by observing the lag between field rotations and the response of ions from the lunar exosphere, we can place constraints on the composition of the ions. Acceleration, Reconnection, Turbulence, and Electrodynamics of Moon’s Interaction with the Sun (ARTEMIS) provides an ideal platform to utilize such an analysis, since its two-probe vantage allows precise timing of the propagation of field discontinuities in the solar wind, and its sensitive plasma instruments can detect the ion response. We demonstrate the utility of this technique by using fully time-dependent charged particle tracing to analyze several minutes of ion observations taken by the two ARTEMIS probes ~3000–5000 km above the dusk terminator on 25 January 2014. The observations from this time period allow us to reach several interesting conclusions. The ion production at altitudes of a few hundred kilometers above the sunlit surface of the Moon has an unexpectedly significant contribution from species with masses of 40 amu or greater. The inferred distribution of the neutral source population has a large scale height, suggesting that micrometeorite impact vaporization and/or sputtering play an important role in the production of neutrals from the surface. Our observations also suggest an asymmetry in ion production, consistent with either a compositional variation in neutral vapor production or a local reduction in solar wind sputtering in magnetic regions of the surface.
1. Introduction and Context
Since the Apollo era, the lunar exosphere has drawn scientific interest. As the nearest example of the wide variety of airless bodies in our solar system, the Moon remains the type example of a surface-boundary exosphere, where the surface rather than a collisional atmosphere forms the lower boundary. However, despite compelling scientific questions, our knowledge of the exosphere’s structure and composition has remained fragmentary until quite recently.
Though a number of in situ and spectroscopic investigations have been conducted, until a few years ago we had obtained direct detections of only a handful of neutral species, notably including argon, helium, sodium, and potassium [Hoffman et al., 1973; Potter and Morgan, 1988; Stern, 1999], but only upper limits on most others [Feldman and Morrison, 1991; Flynn and Stern, 1996; Cook et al., 2013]. In large part, this owes to the sheer tenuousness of the lunar exosphere, and the difficulty of detecting minor species in neutral form above background. Thanks to the high sensitivity and low background of ion mass spectrometers [Hartle and Killen, 2006], many lunar species were first or solely detected in charged form, as pickup ions accelerated by the motional electric field of the surrounding plasma [Freeman and Benson, 1977; Hilchenbach et al., 1991; Mall et al., 1998; Tanaka et al., 2009; Yokota et al., 2009; Poppe et al., 2012; Halekas et al., 2012, 2013, 2015].
The Lunar Atmosphere and Dust Environment Explorer (LADEE) mission, the first spacecraft dedicated to the study of the lunar exosphere, has filled in a number of gaps in our understanding of this unique region. LADEE’s measurements determined the majority composition of the exosphere and uncovered previously undetected species such as neon, aluminum, titanium, and magnesium [Benna et al., 2015; Colaprete et al., 2016]. Perhaps more importantly, LADEE observations have led to a new understanding of the variability of a number of key species, resulting from a combination of spatial and temporal variations in the sources and sinks of the exosphere [Benna et al., 2015; Colaprete et al., 2015; Hodges and Mahaffy, 2016].
However, despite the great strides forward in our understanding of the lunar exosphere, some aspects remain uncertain. In particular, the distribution and variability of the high-altitude exosphere (with the exception of sodium and potassium, observable from Earth [Potter and Morgan, 1988]) remains largely unexplored. To investigate this regime, pickup ions provide the highest signal to noise ratio measurement for many species. The twin Acceleration, Reconnection, Turbulence, and Electrodynamics of Moon’s Interaction with the Sun (ARTEMIS) probes [Angelopoulos, 2010], each of which makes comprehensive measurements of the charged particles and the fields that guide their motion, provide an excellent platform for observing these charged products of the exosphere. However, since the ARTEMIS instruments [McFadden et al., 2008] unfortunately do not directly measure ion composition, we must employ a variety of indirect techniques to infer the composition of the observed ions [Halekas et al., 2012, 2013; Poppe et al., 2012]. To date, only time-stationary time periods have been analyzed in detail. We will now demonstrate that periods with time-varying fields can provide significant new constraints on the composition and structure of the high-altitude lunar exosphere.
2. Ion Acceleration in Time-Varying Fields
Newly born ions from the lunar exosphere feel forces from the interplanetary magnetic field (IMF) and from the motional —v × B electric field produced by the flow of the bulk plasma, which lead to acceleration and eventual incorporation into the bulk flow of the solar wind (“pickup”). In the solar wind, the resulting motion has a characteristic scale large compared to the Moon; as a result, near the Moon we observe only a fraction of the gyroorbit of the ions, dominated by the initial acceleration in the motional electric field. This results in an extended plume of ions accelerated laterally outward from the exosphere, which the two ARTEMIS probes can observe if the electric field lies close to the near-ecliptic planes of the orbits [Halekas et al., 2012].
The IMF, far from maintaining a steady orientation, changes constantly, with Alfvén waves permeating the interplanetary medium [Belcher and Davis, 1971] and causing correlated fluctuations in the flow velocity and magnetic field as flux tubes move in a coherent fashion. Therefore, ions accelerated in the solar wind rarely experience steady magnetic and electric fields during their gyromotion. While high-frequency (short wavelength) fluctuations have a stochastic effect better treated statistically, lower frequency fluctuations have wavelengths large compared to the scale of ion gyromotion, and we can directly take the effects of these large-scale rotations into account when simulating the motion of newly born ions from the lunar exosphere.
On 25 January 2014, the two ARTEMIS probes each crossed a plume of accelerated ions at a distance of ~4000–6000 km from the dusk terminator of the Moon. Probe 2, in a prograde orbit, crossed this plume from the upstream side to the downstream side. Probe 1, in a retrograde orbit, crossed from the downstream side to the upstream side. Given the relatively broad spatial distribution of the plume, both probes observed it for durations of tens of minutes, with a fortuitous overlap in time between the two observations. Figure 1 shows a subset of the observations during this time period from the fluxgate magnetometer (FGM) [Auster et al., 2008] and electrostatic analyzer (ESA) [McFadden et al., 2008] instruments. A number of large Alfvén waves passed over both spacecraft and the Moon during this time period, with a pair of sharp discontinuities passing in the interval between 14:01 and 14:03 that rotated the motional electric field from a dominantly +Ey configuration, to a dominantly +Ez orientation, and back to +Ey. These rotations caused the pickup ion flux to drop out (as the plume rotated away from the ecliptic) and then reappear. The ARTEMIS probes both observed a delay between the field rotations and the ion response, as expected since the ions have a finite travel time from their origin to the probe locations. We will show that we can exploit this hysteresis to constrain the dominant ion species the ARTEMIS probes observed.
Figure 1.

Differential energy flux (eV/(eV cm2 s sr)) for ions observed with spin plane angles of 240–270° and all polar angles (corresponding to velocities 90—120° from the sunward direction), bulk solar wind flow velocity, interplanetary magnetic field (IMF), and —v × B motional electric field at the two ARTEMIS probes P1 and P2. The vertical lines mark two major rotations in the IMF. All vectors utilize Selenocentric Solar Ecliptic (SSE) coordinates.
The fields and flow velocities observed by the two probes have a slight time offset, which changes over the interval shown in Figure 1. By taking into account this time delay, the positions of the two probes, and the propagation of a macroscopic structure traveling with the solar wind flow, we can constrain the orientation of the discontinuities seen by ARTEMIS (which we must do in order to determine when they convect past the points of origin of the observed lunar ions). For the second of the two large rotations in the interval 14:01–14:03 (the “turn-on” discontinuity), we find that the discontinuity normal has roughly equal +x and +y components, as shown graphically in Figure 2. Since both probes lie near the ecliptic, we cannot determine the z component of the discontinuity normal from this simple analysis. A minimum variance analysis of P2 magnetic field data indicates a normal direction of [0.67, 0.69, −0.26], helping confirm the orientation of the discontinuity in the x-y plane and suggesting only a small z component to the discontinuity normal. Regardless, all of the ion trajectories we consider lie close to the ecliptic, so any tilt of the discontinuity plane out of the ecliptic would have little effect on the analysis. This orientation, together with P1’s greater distance from the Moon in the +y direction, ensures that the discontinuity passes P1 first, despite the fact that P1 lies slightly downstream from P2. It also implies that the discontinuity will pass the subsolar point of the Moon ~12 s after it passes P2, and ~17 s after it passes P1. We must take this time shift into account to perform an accurate analysis of the travel times of the ions from their points of origin. The first discontinuity (the “turnoff” discontinuity, which will prove less critical to our analysis), has a very similar inclination, but with a slightly larger y component to the normal (as apparent from the slightly larger time delay between its passage by the two probes).
Figure 2.

The trajectories of the two ARTEMIS probes projected to the ecliptic plane, in SSE coordinates, with the discontinuity encountered just before 14:03 (the second of the rotations marked in Figure 1) shown as it passes the positions of P1, P2 (5 s later), and the subsolar point on the Moon (17 s after passing P1, 12 s after passing P2). The discontinuity orientation was determined from the position of the two probes, the bulk solar wind flow velocity VSW (shown on both sides of the discontinuity) and the relative timing of the two probe’s encounters with the discontinuity.
While we can analytically determine the trajectories of ions that will pass a given position at a given time in constant fields [Halekas et al., 2012, 2013], the presence of field fluctuations and/or rotations makes this impossible. Instead, we resort to an iterative technique to find the ion trajectories that will reach the two probes at each time. One could use either a forward or an inverse technique; however, we found it computationally easier to conduct forward modeling, since all newly born ions from the exosphere start with zero energy. At each start time, we trace ions starting with zero energy (newly ionized particles) from a line in the x-y plane, crossing the subsolar meridian 500 km from the lunar surface and extending to y = ±3000 km (we have tested different initializations and found that the exact details prove unimportant to the subsequent iteration). We trace particles using time-dependent magnetic fields and time-dependent motional electric fields determined from —v × B. To determine the fields at each given point and time along each ion trajectory, we extrapolate from the measurements at the probe, assuming that all fluctuations are planar structures convecting with the solar wind, with the same orientation as the discontinuity analyzed in Figure 2. We then use a Runge-Kutta method with an adaptive time step to determine the trajectory of each ion. In general, the trajectories from this arbitrary set of origins do not intercept the probes. We therefore perform an iterative optimization wherein we find the closest approach between the ion trajectory and the probe (in a fully time-dependent sense), shift the origin according to the displacement between the trajectory and the probe at that closest point, retrace the particle trajectory, and continue until we either reach convergence, or exceed a maximum iteration threshold and discard the trajectory. For steady fields, we only need a single iteration to reach convergence, but for time-varying fields we often require several iterations, since each shift in the origin also changes the fields encountered along the ion trajectory. For each successful trajectory, we record the starting position and time, the travel time, the arrival time at the probe, and the velocity of the ion when it reaches the probe. By utilizing this method for each probe, start time, and species, we can determine a line of origins of trajectories intercepting each probe, for each species, for each start time (moment of ionization).
Figure 3 shows a sample of the resulting derived trajectories from this time period. Figure 3 (top row) shows the lines of origin for eight representative ion species launched at 14:04:09, after the passage of both of the discontinuities discussed above, during relatively steady field conditions. Note that each of these particles will reach the spacecraft at a slightly different time and location, since they have different travel times and the spacecraft moves during their flight. Despite this complication, these lines of origin and trajectories still essentially replicate the analytic solutions in steady fields [Hartle and Killen, 2006; Halekas et al., 2012], as expected given the steady field at this time. We see that at this time, the ARTEMIS probes sample the trajectories of ions born from a broad region lying within a few thousand kilometers of the sunlit lunar surface. Because heavy ions follow less curved trajectories, ARTEMIS samples the trajectories of heavier ions originating closer to the surface, and lighter ions originating farther from the surface.
Figure 3.
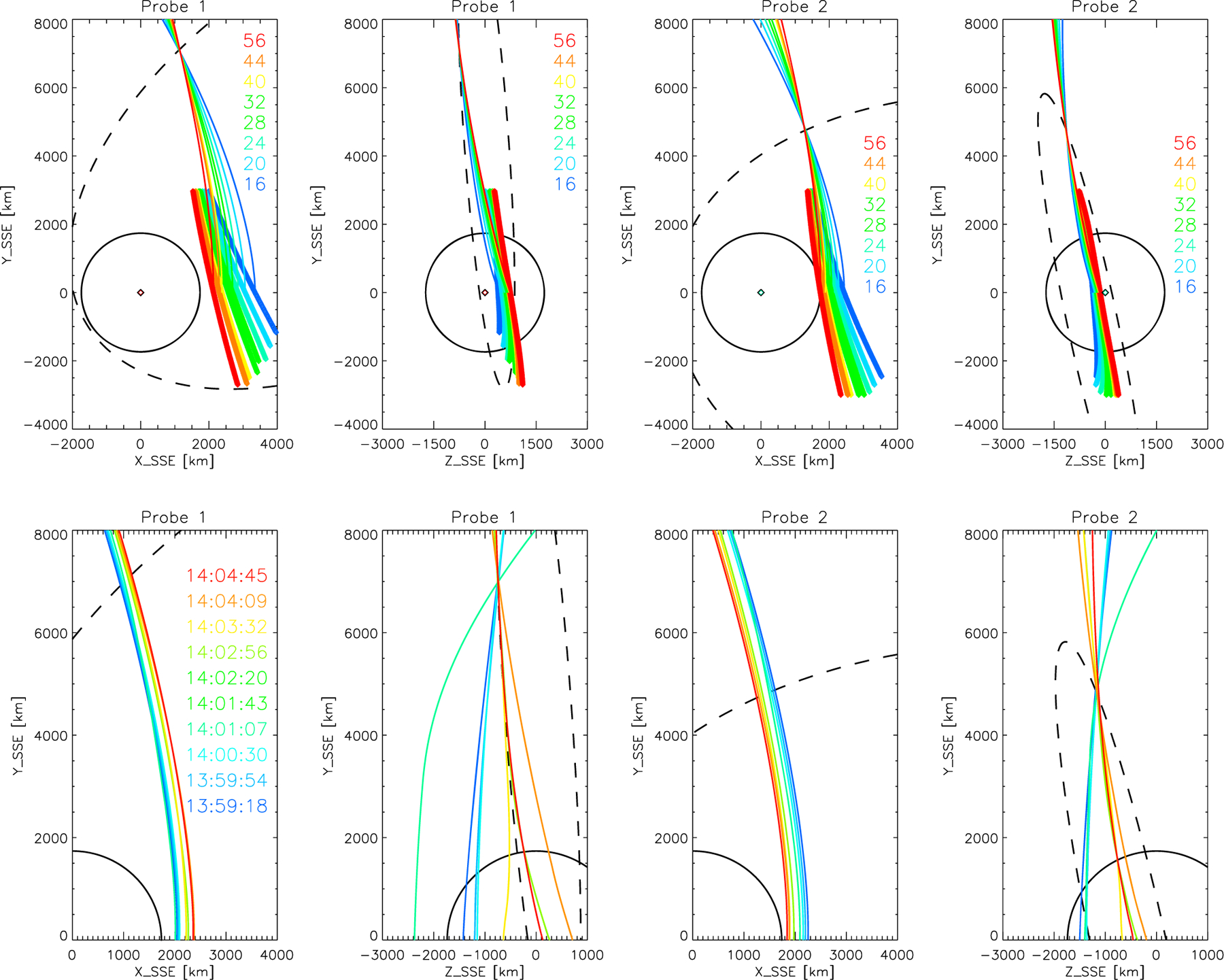
Sample ion trajectories that would reach P1 and P2, in SSE coordinates, as determined from an iterative particle tracing algorithm using time-varying fields inferred from P1 and P2 observations. (top row) Lines of origins (thick lines composed of small diamonds) and sample trajectories from the subsolar meridian for ions of eight different species launched at 14:04:09 with starting positions within one lunar radius of the surface and an initial y coordinate between ±3000 km. Note that each trajectory reaches the probes at a slightly different time and location, since each ion species travels at a different speed. (bottom row) Sample trajectories for 40 amu ions launched from the subsolar meridian at 10 different times. All trajectories for these eight species during this time period originate and remain above the lunar surface.
The ion trajectories that reach the probes evolve over time, as the fields change and the probes move. Figure 3 (bottom row) shows representative trajectories for 40 amu ions launched at 10 start times during the interval in question. Most of these trajectories remain fairly similar to the analytic solutions for constant fields. However, particles that experience large field rotations during their flight follow perturbed trajectories. For instance, ions launched from the subsolar meridian at 14:01:07 experience the first major rotation, the turnoff discontinuity that shuts off Ey and increases the Ez component of the electric field. As a result, this trajectory starts at a much more negative z coordinate, and the trajectory deflects significantly at the time of the field rotation. For start times between the two discontinuities, the dominant Ez ensures that no ions starting near the Moon reach the probes, and thus, Figure 3 shows no trajectories at these times. After the passage of the second discontinuity and rotation back to a dominant Ey, we again find more typical trajectories. As expected, this picture changes for each ion species, as well as for trajectories starting away from the subsolar meridian. In the next section, we will demonstrate that we can exploit these species-dependent effects to extract ion composition information.
3. Nature’s Time-of-Flight Mass Spectrometer
The time-varying fields observed during this time period, while making it substantially more challenging to trace the trajectories of newly born ions from the lunar exosphere, also provide an opportunity to better constrain the dominant species of ions that the ARTEMIS probes observe. Ions take an appreciable time to reach the probes from their origins (tens of seconds for lighter species to ~1 min for heavier species), leading to an observable lag between the passage of discontinuities and the observed response in the ions.
We can predict the approximate form of the observed lunar ion energy distribution for two different kinds of discontinuities, neglecting for the moment the effect of the magnetic field since the observed trajectories have only a small gyrophase at the probes and therefore depend mostly on the electric field (simulated trajectories take into account all fields and all field components—these simple calculations merely provide a first approximation to guide our thinking).
The first case, when the electric field component in the ecliptic suddenly turns off, results in a slow decrease in the energy of the observed ions, since to first approximation, all ions in flight before the field shuts off reach the probes with the energy they had at the time of the shutoff, while none born after the shutoff reach the probes. In this case, if the longest ion trajectory travels a lateral distance L and gains an energy Emax equal to the product of L and the electric force qE, then the flight time tf of observed ions as a function of their final energy Ef will follow:
| (1) |
Thus, after a turnoff of the electric field, one should expect to see a decline in the observed energy with time, with a shorter time constant for lighter ions. For a real rotation that takes a finite amount of time (rather than a sudden discontinuity), the ion trajectories will spread out even more in time. The first of the discontinuities highlighted in Figure 1 had this form, and indeed, the two probes did observe a slow decline in ion energy after the discontinuity passed. Note that there was still a finite electric field perpendicular to the ion trajectories, but this did not greatly change the form of the observed energy decline.
For the second representative case, when the electric field component in the ecliptic suddenly turns on, the flight time between the discontinuity passage and the arrival of ions from a distance L (with final energy Ef equal to the product of L and the electric force qE) will follow:
| (2) |
Thus, after a sudden turn-on in the electric field, one should expect to see a delay before the arrival of the first ions, with the delay proportional to the square root of the ion mass. For a real rotation that takes a finite amount of time (rather than a sudden discontinuity), the ion trajectories will pile up in time, since particles born later experience a higher integrated electric field and catch up to those launched earlier. Thus, one can expect to see enhanced fluxes at the leading edge of the ion plume launched by a sudden turn-on in the electric field. The second of the discontinuities highlighted in Figure 1 (the one shown graphically in Figure 1) had this form, and indeed, both probes observed a sharp turn-on in the ion flux, with a significant delay from the passage of the discontinuity. Probe 2 observations appear to show some evidence of a pileup at the leading edge of the ion front, while Probe 1 observations do not clearly show such a feature.
The two probes observed the first high ion fluxes after the turn-on in energy bins with their centers at 9100 eV and 5320 eV. Given the average observed Ey component of ~1.5 mV/m for this interval, this corresponds to ions that have traveled over lateral distances Δy = L of ~6066 km and ~3550 km, indicating a launch point ~1000 km to the duskside of the subsolar point. Based on the analysis of the turn-on discontinuity shown in Figure 2 and discussed in section 2, it should pass a point ~1000 km duskward of the subsolar point at 14:02:46. The two probes observe the first substantial fluxes after turn-on at 14:03:40 and 14:03:34, respectively, corresponding to flight times of 54 and 48 s. Given these values and the simplified assumptions of equation (2), we would predict an ion mass of 35 amu at Probe 1 and 47 amu at Probe 2. Note that these should represent minimum mass estimates, since any ion born farther upstream from the subsolar point (as Figure 3 shows many of the observed trajectories must) would encounter the discontinuity at an earlier time and have a correspondingly longer time of flight (implying a higher mass).
While the simple calculations discussed above can guide our thinking, we must perform the full time-dependent iterative tracing of ion trajectories described in section 2 to fully capture the time dependence of the observed fields (with no simple turn-ons or turnoffs, but more complicated rotations that each take a finite time), the effects of out-of-plane field components, and the extended nature of the source region. Figure 4 shows representative ion energies and arrival times at the locations of the two probes, as derived from our fully time-dependent iterative tracing, and compared to the observations from the two probes. To first order, these results confirm the results from the simple 1-D analysis of turnoff and turn-on discontinuities given above. However, since Ey only goes completely to zero for a short time, the observed transitions prove slightly less distinct than one would conclude from the simple analysis. The out-of-plane field components present in the time between the two discontinuities also play a role, leading to complex trajectories (see also Figure 3) and moving the origins of the trajectories observed by the probes far from the Moon. For heavier ions, multiple discontinuities can even play a role in the ion motion, as seen for some 44–56 amu ions that experience both the turnoff and turn-on discontinuities while in flight, “coasting” after the first and reaccelerating after the second.
Figure 4.

Differential energy flux (eV/(eV cm2 s sr)) spectra for ions observed by P1 and P2 with spin plane angles of 240–270°, for a subset of the time period in Figure 1. The colored points indicate sample observation times and final energies for ions of eight different species with trajectories that reach the two probes (as determined from iterative particle tracing), launched at evenly spaced times from points along the respective lines of origins with Y coordinates of −900 km, 0 km, and 900 km. The vertical dashed lines show the times of observation of the two discontinuities at the two probes.
From the results shown in Figure 4 we can reach several important conclusions. First, the narrow range of observed energies indicates that the sources of most of the observed ions must lie within a few thousand kilometers of the subsolar meridian, and an apparent bias toward higher fluxes at lower energies (in marked contrast to expectations, given the larger energy bins at higher energies) suggests that more ions come from locations on the duskside of the Moon than from the dawnside (except perhaps for the P2 observations before the passage of the two discontinuities), presumably reflecting the neutral source distribution. Second, given the different prevailing electric field directions before and after the passage of the discontinuities (more −Ez in the latter time period, implying ion origins from a more northerly latitude—see Figure 3), the difference in observed energies during these two time periods (most apparent for P2) suggests a latitude-dependent local time dependence in ion production rate, also presumably reflecting the neutral source distribution. Third, the turnoff discontinuity does not provide a strong constraint on the dominant ion species, but the comparison between simulations and observations appears to favor a majority contribution from ions with masses at or above ~30 amu. Fourth, the comparison between observations and simulations after the turn-on discontinuity suggests that the dominant ion species lies between ~40 and 56 amu (with heavier ions favored for the P2 observations), with no more than a ~10% contribution to the observations at either probe location from ions with masses <~28 amu. In the next two sections we discuss several methods we can use to make these conclusions more quantitative.
4. Inferred Ion Production Rates and Exospheric Source Structure
Now that we have derived some constraints on the species of the ions that the ARTEMIS probes observed during the time period in question, we can go a step further and estimate the ion production rates necessary to produce the observed fluxes. In order to do this, we take the full ensemble of reconstructed trajectories, evenly spaced in launch time and start position along the line of origins. We then convolve each trajectory with the expected energy-dependent and angle-dependent instrument response. As described in McFadden et al. [2008], the ESA ion sensors have intrinsic resolution in energy and spin plane angle (phi) of ~18% ΔE/E and ~6° full width at half maximum, and an essentially constant response in the angle out of the spin plane (theta), with discrete anodes providing variable resolution (higher near the spin plane). In magnetospheric mode, the data processing unit sums four energy bins and two phi bins together to cover a ~28% ΔE/E and 22.5° and sums multiple theta bins to cover 22.5°. This creates a nonuniform response within each summed energy-angle bin, particularly in the phi angle, where the sensitivity varies over a factor of ~4. To account for this, we keep track of where each simulated trajectory lands in the energy-angle map for each probe and apply a variable detection efficiency corresponding to the expected sensitivity at that point. We then sum all trajectories contributing to each measured energy-time bin, which allows us to perform an approximate inversion to determine the ion production rate associated with each point along the line of origins, at each time. Assuming uniform production as a function of time along the portion of the line of origins contributing to each energy-time bin, we can spatially map the production rate so derived, as shown in Figure 5 for 40 amu ions (the map changes slightly for other species but maintains the same key characteristics). This map does not resolve local time structure at scales below the column covered by a single energy bin, about ~1500–2000 km in this case, and so provides only a first-order view of the global structure of the production rate. As shown in Figure 5, we infer peak ion production rates on the order of 10−3 cm−3 s−1 at the locations from which the trajectories sampled by the two ARTEMIS probes originate.
Figure 5.

Inferred ion production rates for 40 amu ions from iterative particle tracing, assuming uniform production along the portion of the line of origins that contributes to each energy-time bin in the energy spectra observed by P1 and P2 during the time period of Figure 4, and no contribution from any other species. Red contours show the surface crustal magnetic field strengths of 20, 50, and 100 nT measured by the Lunar Prospector Electron Reflectometer [Halekas et al., 2001].
The map in Figure 5 has a number of interesting features. We note an apparent local time asymmetry in the production rate, with more production from the duskside than the dawnside, though we find less evidence for local time asymmetry at high southern latitudes. This supports our tentative conclusions based on the energy-time distribution shown in Figure 4 and discussed in section 3, though we must take some care in interpreting this asymmetry, since the source regions we observe on the duskside have a lower altitude than the source regions on the dawnside (which will also produce an apparent asymmetry). The forward modeling discussed in section 5 will further investigate the observational significance of the asymmetry. Taken at face value, the inferred local time asymmetry appears rather puzzling, since many neutral species should have higher densities on the dawnside. Any species that can adsorb and desorb from the surface, including argon and many volatiles, should have a peak near-surface density on the dawnside, since a large quantity of neutrals desorb from the surface as it rotates into sunlight. Species for which micrometeorite vaporization plays a dominant role should also have a peak on the dawnside, since an analysis of LADEE/LDEX data by Szalay and Horányi [2015] shows that the dominant micrometeorite flux during this time period comes from local times of 5–8 A.M.
Two alternative explanations present them-selves. First, the results of Hodges and Mahaffy [2016], Benna et al. [2015], and Colaprete et al. [2015, 2016] show that the sources and/or sinks of many neutral species can vary dramatically over the lunar surface. The subsolar point at the time of the observations lies at a lunar east longitude of −114°. This places the nearside maria on the dusk side of the Moon, including the Mare Procellarum region around −45° that Benna et al. [2015] and Hodges and Mahaffy [2016] found to provide a higher source and/or reduced sink for argon. Spectroscopic observations also suggest a higher source rate for sodium and potassium for east longitudes of −60° to 0° [Colaprete et al., 2015, 2016], which would straddle the dusk terminator at this time. Therefore, a compositional variation in neutral density appears plausible, though such a variation might lead to a distribution even more skewed to the dusk side than what we observe.
A second possibility lies in the work of Poppe et al. [2014], who found that lunar magnetic anomalies could lead to a depression in the efficiency of sputtering by shielding portions of the lunar surface from the solar wind flux and by slowing incoming particles and thereby reducing their sputtering efficiency. At the time of the observation, the strong southern farside anomalies covered most of the region at the dawnside and therefore could suppress the sputtering of neutrals in that region. The strongly magnetized Gerasimovich region lies near the subsolar meridian at this time and could also suppress the sputtered flux of neutrals (note that in Figure 5 this anomaly appears to lie at the edge of but within a region of high inferred production rates; however, the low effective resolution of our mapping makes the location of the transition between high and low production rates greatly uncertain). A variation in sputtering therefore also seems plausible, and such an effect could potentially explain both the inferred local time asymmetry and the latitudinal variation of that asymmetry.
We have also considered a third possibility, namely, a contribution from ions directly sputtered as charged particles from the surface. Solar wind sputtering can directly generate ions from the surface [Elphic et al., 1991], and Sarantos et al. [2012a] predicted fluxes of surface ions of some elements comparable to or greater than those of the same species produced from the neutral exosphere. While plausible at first glance, we tentatively rule out surface ions as a major contributor, based on the overall time dependence of the ion flux observed by the two ARTEMIS probes. As the probes move in their orbit, they sample different lines of origins. If surface ions played a major role, we would have only observed them when the line of origins intersected the surface (given the known orbits, and assuming our tracing algorithm produces exact results, this should have occurred just before the time period in Figure 4 for P1, and just after for P2), leading to a sharp transition in the magnitude of the observed fluxes as the line of origins crosses from the surface to free space. However, Figure 1 shows a smooth evolution of fluxes with time (and orbital position) before and after the time period we analyzed in detail, with no obvious sharp transitions in flux other than those associated with field rotations. This provides strong support for a primary role for ions produced by ionization of exospheric particles at this time.
We now must discuss the magnitude of the observed production rates. A number of observational studies have constrained neutral source densities [Feldman and Morrison, 1991; Flynn and Stern, 1996; Stern, 1999; Cook et al., 2013]; however, these studies placed only upper limits on many species. We therefore compare our inferred production rates to modeled distributions [Wurz et al., 2007; Sarantos et al., 2012a, 2012b; Poppe et al., 2016]. The Poppe et al. [2016] paper (which incorporated the results from the other cited works) provides the most directly comparable result, since they calculated ion production rates as a function of altitude, utilizing photoionization rates [Huebner and Mukherjee, 2015] appropriate for this time period. For altitudes of a few hundred kilometers above the subsolar point, this set of models predicts a total ion production rate of a few times 10−3 cm−3 s−1, comparable to the peak values of 8.8 × 10−4 cm−3 s−1 and 1.6 × 10−3 cm−3 s−1 that we infer from P1 and P2 observations. However, the model predicts Al+, CO+, Na+, K+, and Si+ as the dominant species in this altitude range, in order of importance. Of these species, only K+ lies in the mass range our observations favor. Other species in the favored mass range, namely, Ca+, Ti+, and Fe+, have modeled production rates of 10−6 cm−3 s−1 to a few times 10−5 cm−3 s−1, apparently too low to play a primary role. Given nominal solar wind conditions (density of ~3–4 cm−3 and velocity of 350 km/s), no apparent observational evidence for enhanced micrometeorite impact vapor production in the LDEX data [Horányi et al., 2015], and no observational reason to expect enhanced photoionization during this time period (i.e., no major flares occurred), we can find no reason to suspect an abnormally elevated production rate. At this point, we have no obvious satisfactory explanation for this discrepancy. Potassium (K+) seems to provide the most likely candidate given our present knowledge, but this would require higher than expected production of K+ relative to Na+ and Al+, even when accounting for the fact that the probes effectively sample higher altitudes for these lighter species (see Figure 3). We do note that Kaguya observations indicate a high flux of K+ ions compared to Al+ and Na+, even at a fixed 100 km altitude [Yokota et al., 2014], so we take this possibility seriously. Another plausible contribution to a hot heavy exospheric population could come from photodissociation of oxides such as CaO and FeO, which could lead to a hot population of dissociation byproducts, as recently observed at Mercury [Killen and Hahn, 2015]. For now, we set aside this issue and move forward to consider whether we can better constrain the structure of the neutral source distribution by forward modeling the ion flux from a given source distribution, rather than inverting the observations as described above.
5. Forward Modeling and Comparison to Observations
While the analysis described in section 4 provides a first-order picture of the global distribution of ion production contributing to the ARTEMIS observations, it cannot inform us about the local time structure at scales smaller than the source column covered by a single energy bin. Therefore, we forward model ion production from assumed source distributions in order to better constrain the structure of the neutral source. We consider four source distributions, derived from physics-based considerations. First, we consider a simple exponential function. We fully recognize that the altitude distribution of a collisionless exospheric gas does not follow hydrostatic equilibrium [see, e.g., Hodges and Mahaffy, 2016], particularly for gases produced by sputtering, which have a nonthermal distribution of initial velocities [Wurz et al., 2007]. Nonetheless, this distribution provides a computationally simple form for a distribution that falls with altitude and allows us to constrain an “effective temperature” for the neutral distribution of a given species, based on an effective scale height λ = kT/mg. At great distances from the Moon, most atoms escape, and the distribution should tend toward a 1/r2 form, so we also consider this distribution. Neither of these forms has any solar zenith angle (SZA) dependence; however, for a sputtering source, we would expect a distribution peaked in the subsolar direction. We represent this by multiplying the exponential distribution by a cos2(SZA) functional dependence. Finally, in order to consider the effects of a local reduction in neutral production, due to either compositional differences or shielding of the surface by magnetic anomalies, we consider a “cutout” version of the SZA-dependent exponential distribution, where we suppress all ion production for origins with y < −500 km and z > −1000 km (in Selenocentric Solar Ecliptic (SSE) coordinates), mimicking the dropout inferred from the analysis shown in Figure 5.
Taking each of these four assumed forms for the neutral distribution, and varying both the species and scale height (at least for the three exponential-based distributions), we forward model an ensemble of trajectories based on uniform ionization of the neutral source population, and subsequent acceleration in the time-dependent fields inferred from ARTEMIS observations. We arbitrarily normalize the resulting energy-time distributions to have the same average as the observations for all points with fluxes above that expected for random background. In effect, we thereby normalize out the absolute ionization cross section from this analysis.
Figures 6 and 7 show a sample of the resulting model distributions of ion differential energy flux, as compared to observations from the two probes. As we saw in section 4, modeled distributions for ions with masses <~40 amu do not fit the observations from either probe. Considering only the time dependence (Figures 6 (right column) and 7 (right column)), all four models fit the observations rather well for higher masses. The 1/r2 distribution fits the time dependence of the P1 observations better than exponential models with a 500 km scale height, while the exponential models fit the time dependence of the P2 observations better. When considering the full energy-time dependence (Figures 6 (left column) and 7 (left column)), the cutout distributions fit the observations best for both probes.
Figure 6.

Comparisons between forward modeled and observed differential energy fluxes for four different ion species at P1. (right column) The total observed pickup ion differential energy flux, as compared to the results of four different neutral source models. (left column) The differential energy fluxes from the “cutout” model in color, as compared to the observed fluxes shown by the logarithmically spaced white contours.
Figure 7.

Comparisons between forward modeled and observed differential energy fluxes for four different ion species at P2, in the same format as Figure 6.
We can quantify the agreement of the forward modeled and observed energy-time distributions by calculating the normalized RMS deviation (NRMSD) between model and observation, after the normalization described above. Figure 8 shows the results for the full ensemble of models we considered, for the three exponential models. For both probes, all three models give fairly comparable minimum NRMSD values, but the cutout model results in the deepest and broadest minimum for both probes, lending credence to the existence of a spatially inhomogenous neutral source population. Figure 9 shows the approximate exospheric neutral density structure implied by these fits for the exponential distribution with solar zenith angle dependence, with the inferred cutout location indicated. For all source models, the observations strongly disfavor a majority contribution from ions with masses <~30 amu, with the best fits found for masses of 40–56 amu. The results for all source models also favor a scale height greater than a few hundred kilometers, with the best fits for scale heights of 300–1000 km for most models. This implies an effective temperature for the neutral source populations of a few thousand to perhaps 10,000 K. These effective temperatures seemingly rule out thermal desorption and strongly disfavor photostimulated desorption as a production mechanism for the neutral source particles and instead suggest micrometeorite impact vaporization and sputtering as the most likely candidates to produce the neutral source population from which we observe ionized products.
Figure 8.

RMS deviations between observed differential energy flux distributions and an ensemble of forward modeled distributions produced by tracing ions from source populations with different neutral species and scale heights, normalized by the maximum differential energy flux observed by each probe, for three different source models, at P1 and P2. Dashed curves show “effective temperatures” for the given neutral species and scale heights.
Figure 9.

Exospheric neutral density structure in the equatorial plane, in SSE coordinates, implied from forward model comparisons to ARTEMIS observations, with the approximate region of the inferred “cutout” in exospheric density below (to the west of) the dashed line.
6. Conclusions and Implications
The full time-dependent treatment of ion acceleration around the Moon opens up a new technique for studying the time and spatial dependence of the lunar exosphere with pickup ion observations from ARTEMIS and other spacecraft. When limited to only time-stationary analysis, the wide angular and energy acceptance of the ARTEMIS instruments provides sensitive measurements of lunar ion flux, but allows us to arrive at only loose constraints on the species of the observed ions [Halekas et al., 2012, 2013]. Now, by properly treating pickup ion acceleration during time-varying fields, especially during “turn-on discontinuities” like that analyzed herein, we can provide much stronger constraints on the dominant pickup ion species, with important implications for the composition and dynamics of the lunar neutral exosphere.
The analysis of the observations described in this paper provides a first proof of concept, but in the future one could apply this technique to the entire ARTEMIS data set, consisting of almost 5 years of observations from two probes. While not every orbit has the appropriate field geometry for ARTEMIS to observe lunar ions or the level of variability needed to provide significant timing constraints, we still have a vast data set to mine. Already, with a few minutes of data from a single orbit, we have reached several interesting conclusions, including the dominance of high-mass ions at altitudes of a few hundred kilometers, and a possible asymmetry in ion production in the opposite sense from expected (higher production on the duskside, rather than the dawnside as expected for neutrals produced by thermal desorption and micrometeorite impact vaporization). By analyzing similar observations throughout the ARTEMIS mission, one could determine whether these observations are representative, or whether they are unique in some way (and if so, why?). This would allow us to answer important questions about the geographical inhomogeneity of lunar exospheric sources and sinks, a frontier of study newly opened up by a combination of theoretical work and the recent LADEE observations, but with many aspects not yet fully understood.
Key Points:
Analyzing the time dependence of ion observations around the Moon allows us to place new constraints on the lunar exosphere
The high-altitude lunar exosphere contains more heavy particles from sputtering and/or micrometeorite impact than expected
The lunar exosphere may be spatially inhomogeneous due to compositional variations and/or reductions in sputtering in magnetic regions
Acknowledgments
This research was supported by the Solar System Exploration Research Virtual Institute. A.R.P. also acknowledges NASA LASER grant NNX13AJ97G. We acknowledge NASA contract NAS5-02099 for supporting the ARTEMIS mission and K.H. Glassmeier, U. Auster, and W. Baumjohann for FGM data provided under the lead of the Technical University of Braunschweig and with financial support through the German Ministry for Economy and Technology and the German Center for Aviation and Space (DLR) under contract 50 OC 0302. ARTEMIS data are publicly available on NASA’s CDAWeb.
References
- Angelopoulos V (2010), The ARTEMIS mission, Space Sci. Rev, 10.1007/s11214-010-9687-2. [DOI]
- Auster HU, et al. (2008), The THEMIS fluxgate magnetometer, Space Sci. Rev, 141, 235–264. [Google Scholar]
- Belcher JW, and Davis L Jr. (1971), Large amplitude Alfvén waves in the interplanetary medium 2, J. Geophys. Res, 76, 3534–3563, 10.1029/JA076i016p03534. [DOI] [Google Scholar]
- Benna M, Mahaffey PR, Halekas JS, Elphic RC, and Delory GT (2015), Variability of helium, neon, and argon in the lunar exosphere as observed by the LADEE NMS instrument, Geophys. Res. Lett, 42, 3723–3729, 10.1002/2015GL064120. [DOI] [Google Scholar]
- Colaprete A, Sarantos M, Wooden DH, Stubbs TJ, Cook AM, and Shirley M (2015), How surface composition and meteoroid impacts mediate sodium and potassium in the lunar exosphere, Science, 10.1126/science.aad2380. [DOI] [PubMed]
- Colaprete A, Wooden D, Cook A, Shirley M, Sarantos M (2016), Observations of titanium, aluminum and magnesium in the lunar exosphere, Proc. Lunar Planet. Sci. Conf, 47. [DOI] [PubMed] [Google Scholar]
- Cook JC, Stern SA, Feldman PD, Gladstone GR, Retherford KD, and Tsang CCC (2013), New upper limits on numerous atmospheric species in the native lunar atmosphere, Icarus, 225, 681–687. [Google Scholar]
- Elphic RC, Funsten HO, Barraclough BL, McComas DJ, Paffett MT, Vaniman DT, and Heiken G (1991), Lunar surface composition and solar wind-induced secondary ion mass spectrometry, Geophys. Res. Lett, 18, 2165–2168, 10.1029/91GL02669. [DOI] [Google Scholar]
- Feldman PD, and Morrison D (1991), The Apollo 17 ultraviolet spectrometer: Lunar atmosphere measurements revisited, Geophys. Res. Lett, 18, 2105–2109, 10.1029/91GL01998. [DOI] [Google Scholar]
- Flynn BC, and Stern SA (1996), A spectroscopic survey of metallic species abundances in the lunar atmosphere, Icarus, 124, 530–536. [Google Scholar]
- Freeman JW Jr., and Benson JL (1977), A search for gaseous emissions from the Moon, Phys. Earth Planet. Inter, 14, 276–281. [Google Scholar]
- Halekas JS, Mitchell DL, Lin RP, Frey S, Hood LL, Acuña MH, and Binder AB (2001), Mapping of crustal magnetic anomalies on the lunar near side by the Lunar Prospector Electron Reflectometer, J. Geophys. Res, 106, 27,841–27,852, 10.1029/2000JE001380. [DOI] [Google Scholar]
- Halekas JS, Poppe AR, Delory GT, Sarantos M, Farrell WM, Angelopoulos V, and McFadden JP (2012), Lunar pickup ions observed by ARTEMIS: Spatial and temporal distribution and constraints on species and source locations, J. Geophys. Res, 117, E06006, 10.1029/2012JE004107. [DOI] [Google Scholar]
- Halekas JS, Poppe AR, Delory GT, Sarantos M, and McFadden JP (2013), Using ARTEMIS pickup ion observations to place constraints on the lunar atmosphere, J. Geophys. Res. Planets, 118, 81–88, 10.1029/2012JE004292. [DOI] [Google Scholar]
- Halekas JS, Benna M, Mahaffy PR, Elphic RC, Poppe AR, and Delory GT (2015), Detections of lunar exospheric ions by the LADEE neutral mass spectrometer, Geophys. Res. Lett, 42, 5162–5169, 10.1002/2015GL064746. [DOI] [Google Scholar]
- Hartle RE, and Killen RM (2006), Measuring pickup ions to characterize the surfaces and exospheres of planetary bodies: Applications to the Moon, Geophys. Res. Lett, 33, L05201, 10.1029/2005GL024520. [DOI] [Google Scholar]
- Hilchenbach M, Hovestadt D, Klecker B, and Mobius E (1991), Detection of singly ionized energetic lunar pick-up ions upstream of Earth’s bow shock, in Solar Wind Seven, edited by Marsch E and Schwenn G, pp. 150–155, Pergamon, New York. [Google Scholar]
- Hodges RR, and Mahaffy PR (2016), Synodic and semiannual oscillations of Argon-40 in the lunar exosphere, Geophys. Res. Lett, 43, 22–27, 10.1002/2015GL067293. [DOI] [Google Scholar]
- Hoffman JH, Hodges RR Jr., and Evans DE (1973), Lunar atmospheric composition results from Apollo 17, Proc. Lunar Sci. Conf, 4, 2875. [Google Scholar]
- Horányi M, Szalay JR, Kempf S, Schmidt J, Grün E, Srama R, and Sternovsky Z (2015), A permanent asymmetric dust cloud around the Moon, Nature, 522, 10.1038/nature14479. [DOI] [PubMed] [Google Scholar]
- Huebner WF, and Mukherjee J (2015), Photoionization and dissociation rates in solar and blackbody radiation fields, Planet. Space Sci, 106, 11–45. [Google Scholar]
- Killen RM, and Hahn JM (2015), Impact vaporization as a possible source of Mercury’s calcium atmosphere, Icarus, 250, 230–237. [Google Scholar]
- Mall U, Kirsch E, Cierpka K, Wilken B, Soding A, Neubauer F, Gloeckler G, and Galvin A (1998), Direct observation of lunar pick-up ions near the Moon, Geophys. Res. Lett, 25, 3799–3802, 10.1029/1998GL900003. [DOI] [Google Scholar]
- McFadden JP, Carlson CW, Larson D, Ludlam M, Abiad R, Elliott B, Turin P, Marckwordt M, and Angelopoulos V (2008), The THEMIS ESA plasma instrument and in-flight calibration, Space Sci. Rev, 141, 277–302. [Google Scholar]
- Poppe AR, Samad R, Halekas JS, Sarantos M, Delory GT, Farrell WM, Angelopoulos V, and McFadden JP (2012), ARTEMIS observations of lunar pickup ions in the terrestrial magnetotail lobes, Geophys. Res. Lett, 39, L17104, 10.1029/2012GL052909. [DOI] [Google Scholar]
- Poppe AR, Sarantos M, Halekas JS, Delory GT, Saito Y, and Nishino M (2014), Anisotropic solar wind sputtering of the lunar surface induced by crustal magnetic anomalies, Geophys. Res. Lett, 41, 4865–4872, 10.1002/2014GL060523. [DOI] [Google Scholar]
- Poppe AR, Halekas JS, Szalay JR, Horányi M, Levin Z, and Kempf S (2016), LADEE/LDEX observations of lunar pick-up ion variability, Geophys. Res. Lett, 43, 3069–3077, 10.1002/2016GL068393. [DOI] [Google Scholar]
- Potter AE, and Morgan TH (1988), Discovery of sodium and potassium vapor in the atmosphere of the Moon, Science, 241, 675–680. [DOI] [PubMed] [Google Scholar]
- Sarantos M, Killen RM, Glenar DA, Benna M, and Stubbs TJ (2012a), Metallic species, oxygen and silicon in the lunar exosphere: Upper limits and prospects for LADEE measurements, J. Geophys. Res, 117, A03103, 10.1029/2011JA010744. [DOI] [Google Scholar]
- Sarantos M, Hartle RE, Killen RM, Saito Y, Slavin JA, and Glocer A (2012b), Flux estimates of ions from the lunar exosphere, Geophys. Res. Lett, 39, L13101, 10.1029/2012GL052001. [DOI] [Google Scholar]
- Stern SA (1999), The lunar atmosphere: History, status, current problems, and context, Rev. Geophys, 37, 453–491, 10.1029/1999RG900005. [DOI] [Google Scholar]
- Szalay JR, and Horányi M (2015), Annual variation and synodic modulation of the sporadic meteoroid flux to the Moon, Geophys. Res. Lett, 42, 10,580–10,584, 10.1002/2015GL066908. [DOI] [Google Scholar]
- Tanaka T, et al. (2009), First in situ observation of the Moon-originating ions in the Earth’s magnetosphere by MAP-PACE on SELENE (KAGUYA), Geophys. Res. Lett, 36, L22106, 10.1029/2009GL040682. [DOI] [Google Scholar]
- Wurz P, Rohner U, Whitby JA, Kolb C, Lammer H, Dobnikar P, and Martín-Fernández JA (2007), The lunar exosphere: The sputtering contribution, Icarus, 191, 486–496. [Google Scholar]
- Yokota S, et al. (2009), First direct detection of ions originating from the Moon by MAP-PACE IMA onboard SELENE (KAGUYA), Geophys. Res. Lett, 36, L11201, 10.1029/2009GL038185. [DOI] [Google Scholar]
- Yokota S, et al. (2014), Structure of the ionized lunar sodium and potassium exosphere: Dawn-dusk asymmetry, J. Geophys. Res. Planets, 119, 798–809, 10.1002/2013JE004529. [DOI] [Google Scholar]


