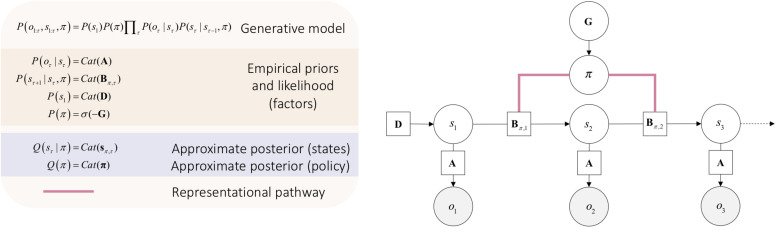
FIGURE 2.

Minimal discrete state space generative model for action. Open circles are random variables (hidden states and policies). Gray filled circles are observable outcomes. Squares are known variables, such as the model parameters. _Cat refers to categorical distributions. The equations in the beige box (upper left) specify the architecture of the generative model (for a complete description see Friston et al., 2017b). The likelihood matrix _A specifies the probability of outcomes for each combination hidden states _s. The novelty of this generative model rests on the addition of a policy _π that determines state transitions, represented by the policy-dependent transition matrix B_π,τ. The initial state is specified by _D. The approximate posterior of the future hidden state s_π,τ at time _t relative to the policy _π is found by evaluating the approximate posterior for the policy _Q(π). This policy will be the one with the least expected free energy _G=–lnP(π) that determines prior beliefs about the policy being pursued; namely _P(π) that can recovered from expected free energy, using the softmax operator _σ (for a complete description see Friston et al., 2017a). Note that the edges that link the policy and the transition matrices are undirected. This is important, as it means that the evaluation of expected free energy requires a message from hidden states representations, thereby affording a representationalist pathway.