Simultaneous polarimeter retrievals of microphysical aerosol and ocean color parameters from the “MAPP” algorithm with comparison to high spectral resolution lidar aerosol and ocean products

Abstract

We present an optimal estimation based retrieval framework, the Microphysical Aerosol Properties from Polarimetry (MAPP) algorithm, designed for simultaneous retrieval of aerosol microphysical properties and ocean color bio-optical parameters using multi-angular polarized radiances. Polarimetric measurements from the airborne NASA Research Scanning Polarimeter (RSP) were inverted by MAPP to produce atmosphere and ocean products. The RSP MAPP results are compared with co-incident lidar measurements made by the NASA High Spectral Resolution Lidar HSRL-1 and HSRL-2 instruments. Comparisons are made of the aerosol optical depth (AOD) at 355 and 532 nm, lidar column-averaged measurements of the aerosol lidar ratio and Ångstrøm exponent, and lidar ocean measurements of the particulate hemispherical backscatter coefficient and the diffuse attenuation coefficient. The measurements were collected during the 2012 Two-Column Aerosol Project (TCAP) campaign and the 2014 Ship-Aircraft Bio-Optical Research (SABOR) campaign. For the SABOR campaign, 73% RSP MAPP retrievals fall within ± 0.04 AOD at 532 nm as measured by HSRL-1, with an R value of 0.933 and root-mean-square deviation of 0.0372. For the TCAP campaign, 53% of RSP MAPP retrievals are within 0.04 AOD as measured by HSRL-2, with an R value of 0.927 and root-mean-square deviation of 0.0673. Comparisons with HSRL-2 AOD at 355 nm during TCAP result in an R value of 0.959 and a root-mean-square deviation of also 0.0694. The RSP retrievals using the MAPP optimal estimation framework represent a key milestone on the path to a combined lidar+polarimeter retrieval using both HSRL and RSP measurements.

1. INTRODUCTION

In this paper, we present a retrieval framework, Microphysical Aerosol Properties from Polarimetry (MAPP), designed to simultaneously retrieve aerosol microphysical properties and ocean color bio-optical parameters using multi-angular polarized radiances from the NASA GISS Research Scanning Polarimeter (RSP [1]). The atmosphere/ocean products are compared against NASA Langley High Spectral Resolution Lidar (HSRL-1 and HSRL-2 [2]) aerosol optical depths and lidar ocean measurements as well as lidar intensive parameters (the lidar ratio and Ångstrøm exponent). The co-incident polarimeter and lidar measurements that are presented were collected during the 2012 Two-Column Aerosol Project (TCAP [3]) campaign and the 2014 Ship-Aircraft Bio-Optical Research (SABOR) campaign. TCAP was a Department of Energy campaign conducted off the coast of Cape Cod to address knowledge gaps in aerosol and cloud temporal evolution and uncertainties in direct and indirect aerosol forcing, by improving remote sensing retrievals of aerosol optical and microphysical properties, and studying aerosol-cloud interactions. Thus the TCAP study sampled the atmosphere between and within two atmospheric columns; one fixed near the coast of North America (over Cap Cod, MA) and a second moveable column over the Atlantic Ocean several hundred kilo-meters from the coast. The NASA-led SABOR campaign was designed to assess the applicability of lidar and polarimetry for ocean biogeochemistry, and involved ship-based in situ measurements as well as airborne remote sensors. The SABOR campaign provides a wide range of ocean optical properties from aircraft overflights of the ship, spanning ocean conditions from the eutrophic waters of the Gulf of Maine to oligotrophic waters near Bermuda.

The aircraft-based RSP instrument can retrieve aerosol/ocean products by measuring the upwelling total and polarized reflectance using six paired refractive telescopes, with each pair making measurements in three spectral bands. One telescope in each pair makes simultaneous measurements of the linear polarization components of the intensity in orthogonal planes at 0° and 90° to the meridional plane of the instrument, while the other telescope simultaneously measures equivalent intensities in orthogonal planes at 45° and 135°. The RSP instrument has nine spectral channels that are divided into two groups based on the type of detector used: visible/near infrared (VNIR) bands at approximate wavelengths (full width at half maximum (FWHM) in parenthesis) 410 (30), 469 (20), 555 (20), 670 (20), 864 (20) and 960 (20) nm and shortwave infrared (SWIR) bands at 1594 (60), 1880 (90), and 2264 (120) nm. The set of four measurements in a particular band are denoted S_1L and S_1R for the two orthogonal polarization states in the telescope observing at polarization azimuths of 0° and 90°, and S_2L and S_2R for the two orthogonal polarizations in the second telescope of each pair. The Stokes parameters I, Q, and U can be derived from these four measurements, and the corresponding orthogonal (parallel and perpendicular) components are obtained as I_L = (I + Q)/2 and I_R = (I − Q)/2, respectively. With appropriate normalization (see Eqs. (23,24,25)), we can also define corresponding reflectances R_I, R_Q, R_U, R_IL, and R_IR.

Waquet et al. (2009) [4] used polarized reflectance (R_Q) observations in seven spectral spectral bands (excluding the 960 and 1880 nm bands) obtained during the 2005 ALIVE campaign in the Southern Great Plains, and in 2003 over the Simi Valley in the Mojave desert to retrieve aerosol microphysical parameters. The 2.26 μm polarized reflectances were primarily used to characterize the polarized surface reflectance as a function of scan angle, which to a good approximation is spectrally invariant. Knobelspiesse et al. (2011) [5] used polarized reflectances rotated into the scattering plane in the same bands used by Waquet et al. (2009) and two total reflectance measurements at 410 and 2264 nm from RSP to retrieve aerosol microphysical parameters of thick smoke over land during the 2008 ARCTAS campaign. Over water, Chowdhary et al. (C2006, C2012) [6, 7] performed simultaneous aerosol and ocean retrievals using total and polarized reflectance observations for RSP observations collected off the coast of Veracruz, Mexico during the 2006 MILAGRO campaign, but focused mainly on development of an ocean bio-optical model for polarized reflectances. Wu et al. (2015) [8] used all seven RSP window channels for total reflectance (R_I) and the degree of linear polarization, $\text{DoLP}=\sqrt{R_Q^2+R_U^2}/R_I$, to retrieve properties of fine and coarse mode aerosol retrievals over land.

One of the main ideas in the “MAPP” algorithm is that the retrieval is “coupled”, in the sense that the atmosphere and ocean products are simultaneously retrieved, and that all seven RSP window channels are used including polarization through both the reflectances R_IL, R_IR, and the degree of linear polarization. While MAPP may not work as well as “hand-tuned” retrievals one might conduct for a few cases, the goal is to produce an algorithm that is capable of automated processing of polarimeter (RSP) data. Also, MAPP was designed not only as a standalone polarimeter retrieval algorithm, but as the foundation for a combined HSRL+RSP retrieval (or arbitrary lidar+polarimeter configuration). The focus of this paper, and a key milestone on the path to the combined HSRL+RSP retrieval, is a MAPP RSP (polarimeter-only) retrieval that provides the framework for processing polarimeter data, and a baseline retrieval which the combined MAPP HSRL+RSP retrieval is expected to improve upon. Thus for the RSP MAPP retrievals in this paper, we use the lidar only to provide the aerosol top height and cloud screening to identify Aerosol-Above-Ocean (AAO) scenes. We present RSP MAPP results for all TCAP Phase 1 and SABOR AAO scenes, after screening for clouds and aircraft altitude/roll.

A unique feature of MAPP is the focus on coupled retrievals of aerosol microphysical properties and ocean color parameters using optimal estimation driven by on-the-fly vector radiative transfer and Mie calculations. The RSP instrument makes coupled retrievals easier in that, unlike an imager which has many scenes (pixels) but fewer measurements per scene, the RSP instrument scans along track so that a single scene contains many measurements per pixel, with fewer scenes to process. Fewer scenes make it possible to perform Mie and vector radiative transfer calculations on the fly, rather than relying on LUTs of pre-computed results. Performing the vector radiative transfer computations on the fly is advantageous for aircraft platforms where the sensor altitude varies and the aerosol location (top height, layering, etc.) is allowed to vary, whereas precomputed Mie LUTs would provide a speed benefit at the cost of reduced flexibility. Over 90% of the signal measured by a spectroradiometer or polarimeter is due to the molecular and aerosol scattering in the atmosphere and the Fresnel reflection of the ocean surface, so that less than 10% of the signal is due to subsurface ocean inherent optical properties (particulate and dissolved matter) [9]. RSP measurements of the polarized reflectance at multiple angles can lead to improved retrievals of underwater properties by enabling accurate characterization of the aerosol signal through retrieval of aerosol optical depth, microphysical aerosol properties, including aerosol effective radius, single-scattering albedo, and the real part of the refractive index. Another advantage is that RSP does not saturate due to sunglint, which is a significant issue for instruments like MODIS.

The overall methodology is described in section 2, and is summarized by the retrieval parameters, which determine the state of the atmosphere (aerosol) and ocean models. In section 3, we present the retrieval framework based on principles of optimal estimation, while section 4 includes descriptions of the instruments, direct measurements, lidar ocean products and noise profiles. Section 5 discusses simulated retrievals, and sections 6 and 7 present results for measurements collected during the SABOR and TCAP campaigns, respectively. Section 8 provides an error analysis and a conclusion is provided in section 9. The RSP MAPP products are summarized on the NASA LaRC HSRL website (https://science.larc.nasa.gov/lidar/microphysics) [10] and are available for download at the NASA GISS RSP website (https://data.giss.nasa.gov/pub/rsp) [11].

2. METHODOLOGY

The MAPP algorithm consists of an optimal estimation based solver, where the forward model consists of a vector radiative transfer code and a Mie scattering code. In optimal estimation theory, the forward model input is specified by the state vector, and the forward model output matches the instrument, in this case RSP’s polarized radiances. Each MAPP retrieval takes approximately 60 minutes to run on a single core of a Sandy Bridge Intel Xeon processor, although we expect to reduce processing (CPU) time by a factor of 2–3. The NASA LaRC K cluster was used to perform the retrievals in parallel, and since the CPU time scales linearly with the number of cores, then 1,000 cores enables processing of approximately 24,000 scenes per 24 hours. Assuming an RSP-like along-track polarimeter was scanning continuously at 1 Hz, averaging to 10 seconds per measurement would result in 8,640 scenes per 24 hours. Hence MAPP is already fast enough to process 10-second-averaged RSP-like data within 60 minutes, given a dedicated resource of approximately 500 Sandy Bridge cores (allowing for some overhead).

A. Overview of MAPP retrieval parameters

The state vector of MAPP retrieval parameters is defined as

$$x=\langle {\tau }_{555f}{r}_{nf}{\sigma }_{gf}{n}_{rf}{n}_{if}{\tau }_{555c}{r}_{nc}{\sigma }_{gc}{n}_{rc}{n}_{ic}vCHL{z}_c{z}_f\rangle$$ (1)

where τ_555f is the fine (accumulation) mode aerosol optical depth at 555 nm, r_nf is the number-density mean radius with geometric width σ_gf, n_rf + in_if is the fine mode refractive index (assumed to be spectrally invariant), τ_555c is the aerosol optical depth of the coarse mode, r_nc is the coarse mode number-density mean radius with geometric width σ_gc. The coarse mode refractive index, n_rc + in_ic, was assumed a priori to be equal to that of water to represent hydrated sea salt (marine) aerosols. The aerosol top heights for the coarse and fine mode were set to be the same (z_f = z_c), and were obtained by finding the altitude that represented an integral of 95% of the lidar backscatter or extinction at 532 nm. For the simulated retrieval z_f and z_c were fixed and assumed to be known. While it is possible to use polarimetric observations to retrieve the aerosol layer height [12] here we assume that high quality lidar observations are available to constrain this aspect of aerosol variability. The ocean surface roughness is described by the windspeed v [m/s] and the subsurface absorption and scattering is parameterized in terms of the chlorophyll concentration CHL [mg/m³]. The ranges allowed for each of the parameters in this 10-parameter retrieval are as follows:

$$\begin{array}{c}{10}^{-5}\le {\tau }_{555f}\le 0.6\\ 0.075\le r_{nf}\le 0.15\mu \text{m}\\ 1.36\le n_{rf}\le 1.65\\ {10}^{-5}\le n_{if}\le 0.03\\ {10}^{-5}\le {\tau }_{555c}\le 0.4\\ 0.5\le r_{nc}\le 1.5\mu \text{m}\\ 0.3\le {\sigma }_{gf}\le 0.7\\ 0.3\le {\sigma }_{gc}\le 0.7\\ 0.01\le v\le 7.0\text{m}/\text{s}\\ 0.001\le \text{CHL}\le 10\text{mg}/{\text{m}}^3.\end{array}$$ (2)

The maximum allowed optical depth for the fine and coarse modes is up to 0.6 for the fine mode, and up to 0.4 for the coarse mode, which are reasonable values for conditions encountered over the Atlantic Ocean off the East coast of the United States, but which need to be increased in areas with higher aerosol loading. The choices for all the aerosol parameters are explained in section 2B.2. The allowed ranges for the windspeed and chlorophyll concentration are explained in section 2C.

B. Atmosphere models

B.1. Atmospheric gases

The atmosphere is assumed to consist of 5 layers between 0 and 100 km to account for the vertical distribution of molecules that scatter and absorb sunlight. For retrievals of real data we used 5 layers with [0, z_aerosol, z_aircraft, 12, 22, 100] km, where z_aerosol is the aerosol top height and z_aircraft is the aircraft altitude, followed by 3 additional layers to allow for some vertical variation in molecular absorption. The molecular absorption is due mainly to trace gases plus O₂, while molecular scattering is driven by N₂ and O₂ gas which comprise the bulk of the atmosphere. For the calculation of absorption by gases in each window channel (band), MODTRAN [13] was used with the Mid-latitude Summer model atmosphere. In addition to the gases N₂ and O₂, the following trace gases were considered: H₂O, H₂O continuum, CO₂, O₃, N₂O, CO, CH₄, NO, SO₂, NO₂, NH₃, HNO₃. The Mid-latitude Summer model was created in the 1980s, and as a result the well-mixed gases that absorb in the RSP channels need to be scaled to current values. The default value of 330 ppmv of CO₂ is scaled to a 2012–2014 value of 400 ppmv of CO₂ using a scaling factor of 1.2. Absorption by water vapor is turned off in the MODTRAN model, and is instead derived using measurements from RSP’s 960 nm channel and the following parameterization for the water vapor column amount, w_col [cm] [14, 15]:

$$w_{\text{col}}=\frac{1}{\frac{1}{\left|{\mu }_g\right|}+\frac{1}{\left|{\mu }_0\right|}}{\left[\frac{\ln \frac{I_{864}\left({\mu }_g\right)}{I_{960}\left({\mu }_g\right)}}{\alpha }\right]}^{1/\beta }$$ (3)

where μ_g is the cosine of the glint angle, μ₀ is the cosine of the solar zenith angle, and α = 0.31607, β = 0.595575 are empirical constants that depend upon RSP’s 960 nm filter response function. The normalized radiances (see Eq. (24) and discussion in section 4A) at the 1594 and 2264 nm shortwave infrared (SWIR) channels are converted to reflectances (Eq. (25)) by the factor $\frac{d_{\text{s}}^2}{{\mu }_0}$ and scaled by T, the transmission due to water vapor:

$$f=\frac{d_s^2}{{\mu }_0}\frac{1}{T}$$ (4)

where $d_S=\frac{\text{Earth–to–Sun distance}}{1\text{AU}}$ is the ratio of the actual Earth to Sun distance to one astronomical unit. The band integrated total transmittance in the RSP SWIR channels is modeled by dividing the radiation into two parts. The first part can be regarded as the fraction of radiation that is in the centers of absorption lines and which represents a negligible (< 1%) fraction of the radiation reflected back to the sensor. The second part is the fraction of radiation that is representative of atmospheric windows together with absorption by line wings and the water vapor continuum. The absorption of this second part of the radiation is well represented by a single absorption coefficient with contributions from both water vapor and well mixed gases. The model for total transmittance therefore only depends on this second part and the total transmittance in the SWIR bands, T, is given by the product of two terms, T = T₀(w_col) × T_B(w_col, μ₀, μ_v). In this equation T₀(w_col) is the fraction of radiation that contributes to the RSP observation, which does not depend on viewing geometry, and T_B(w_col, μ₀, μ_v), which is a Beer’s law model for the transmittance of this radiation. The fraction of radiation that contributes to RSP SWIR channel observations is given by $T_0\left(w_{\text{col}}\right)={\sum }_{i=0}^2\left[c_i{w}_{\text{col}}^i\right]$, for the 1594 and 2264 nm channels. The absorption optical depth for the Beer’s law model is given by ${\tau }_{\text{tot}}\left(w_{\text{col}}\right)\equiv a{w}_{\text{col}}+{\tau }_{\text{well mixed}}$ where τ_tot,1594 = 0.00106669w_col + 0.0146353 and τ_tot,2264 = 0.00438348w_col + 0.03664. (Since we used MODTRAN to compute the absorption optical depth from well mixed gases to use directly in the radiative transfer calculation, τ_{well mixed} was set to zero.) The Beer’s law equation for transmittance is T_tot(w_col, μ₀, μ_v) = exp[−(1/μ₀ + 1/|μ_v|)τ_tot]. The coefficients for the fraction of radiation T₀ and the absorption optical depth τ_tot in this model are derived from calculations of transmittance at 1 nm resolution using a correlated-k distribution model for line absorption that is derived from HITRAN2008, and a physically based water vapor continuum model [16]. The 1 nm resolution transmittances are integrated with a solar spectral weighting over the RSP spectral bands for a wide range of water vapor amounts (0–5 precipitable cm) and air masses (2–5) and the coefficient in the model for RSP SWIR channel total transmittances provide a least mean square best fit to these calculations.

B.2. Aerosol models

Aerosols are assumed to be bimodally distributed, with a fine mode and a coarse mode. The complex refractive index of the fine mode is retrieved. The refractive index of the coarse mode is fixed to that of water, which is a reasonable assumption for hydrated sea-salt particles, particularly considering that the desired retrieval accuracy of the real refractive index is ± 0.02. The atmospheric layer that contains up to 95% of the lidar-backscattered signal above the ocean is assumed to contain all of the aerosol particles, distributed homogeneously. The bimodal lognormal volume-density size distribution is defined by

$$v(r)=\frac{1}{r}\frac{dV(r)}{d\ln r}=\frac{1}{r}\sum _{i=1}^2\frac{V_i}{\sqrt{2\pi }{\sigma }_{gi}}\exp \left[-{\left(\frac{\ln r-\ln r_{vi}}{\sqrt{2}{\sigma }_{gi}}\right)}^2\right]$$ (5)

where the subscript i represents the particle mode, V_i [m⁻¹] is the total volume of particles per unit volume per unit radius, r_vi is the volume geometric mean radius, and σ_gi is the geometric standard deviation. In terms of the number-density, Eq. (5) becomes

$$n(r)=\frac{1}{r}\frac{dN(r)}{d\ln r}=\frac{1}{r}{\sum }_{i=1}^2\frac{N_i}{\sqrt{2\pi }{\sigma }_{gi}}\exp \left[-{\left(\frac{\ln r-\ln r_{ni}}{\sqrt{2}{\sigma }_{gi}}\right)}^2\right]$$ (6)

where the total number of particles N_i [m⁻⁴] per unit volume per unit radius and the mode radius r_ni in number-density space are related to V_i and r_vi by

$$N_i=\frac{V_i}{\frac{4}{3}\pi r_{ni}^3}\exp \left(-4.5{\sigma }_{gi}^2\right),$$ (7)

$$r_{ni}=r_{vi}\text{exp}(-3{\sigma }_{gi}^2).$$ (8)

If we use the subscript i = f to denote the fine mode, and the subscript i = c to denote the coarse mode, we have V = V_f + V_c, and the fraction of fine mode particles in volume-density becomes f_v = V_f/V. The definition of effective radius is

$$r_{\text{eff}}=\frac{{\int }_{r_{\min }}^{r_{\max }}{r}^{3}n(r)dr}{{\int }_{r_{\min }}^{r_{\max }}{r}^{2}n(r)dr}\stackrel{\text{lognormal}}{\equiv }{r}_n\exp \left(2.5{\sigma }_g^2\right)$$ (9)

where the right most expression is for a lognormal distribution. The corresponding effective variance is defined by

$$v_{\text{eff}}=\frac{{\int }_{r_{\min }}^{r_{\max }}{\left(r-r_{\text{eff}}\right)}^2\pi r^{2}n(r)dr}{r_{\text{eff}}^2{\int }_{r_{\min }}^{r_{\max }}\pi r^{2}n(r)dr}\stackrel{\text{lognormal}}{\equiv }\exp \left({\sigma }_g^2\right)-1$$ (10)

where the right most expression is for a lognormal distribution. The effective radius (Eq. (9)) is a more useful parameter than the mode radius because the single-scattering properties depend on the geometrical cross section πr² [17, 18] and for weak absorption the single-scattering albedo is proportional to the effective radius. Thus, aerosols with the same effective radius and effective variance tend to have similar scattering properties independent of size distribution. The aerosol scattering is therefore described more concisely by the effective radius, which is a function of both the mode radius and mode width, rather than by the mode radius alone.

The assumption of a single homogenous aerosol layer was applied to both the simulated data (section 5) and real data (sections 6 and 7). For real data we rely on lidar data to identify the aerosol location; otherwise information about the aerosol location would also have to be retrieved. The inversions of real/simulated data are described in section 3. For inversions of real RSP data, we determined the aerosol height in km from collocated HSRL data, by integrating the measured backscatter from the surface to 95% of the total measured aerosol backscatter, and used the height corresponding to the 95th percentile as the aerosol top height. Thus the aerosols were approximated as being homogeneously distributed between 0 km and the aerosol top height, representing a column aerosol retrieval.

The MAPP aerosol model consists of a Lorenz-Mie [17, 19–21] code that is run on the fly – at each step in the iterative retrieval – to calculate the scattering properties of spherical particles, i.e. the single-scattering albedo and scattering phase matrix needed for polarized radiative transfer calculations. The MAPP aerosol model incorporates fine mode effective radii in the range [0.094 μm, 0.51 μm] and coarse mode effective radii in the range [0.626 μm, 5.1 μm], which extends the size range used in the SeaDAS aerosol model for both modes (see Table 1). The goal is to capture most types of aerosols that can be modeled using spheres.

Table 1.

All sizes in [μm]. Aerosol fine/coarse mode ranges (low, high) from left to right: (i) Seinfeld (2006) p712 [22]. (ii) Seinfeld (2006) p713 average excluding marine using ± 2σ [22]. (iii) SeaDAS model [23]. (iv) Modini (2015) [24]. (v) MAPP aerosol model used in this paper.

Param.	Seinfeld	Seinfeld	SeaDAS	Modini	MAPP
reff,f	0.22, 0.80	0.19, 1.0	0.13, 0.23	0.06, 0.33	0.094, 0.51
rnf	0.09, 0.18	0.08, 0.21	0.08, 0.14	0.05, 0.1	0.075, 0.15
exp σgf	1.84, 2.16	1.8, 2.2	1.54	1.3, 2.0	1.35, 2.01
reff,c	8.76, 70.6	0.23, 64.2	1.93, 4.43	0.57, 2.65	0.626, 5.1
rnc	2.25, 6.0	0.85, 5.45	0.62, 1.43	0.07, 0.13	0.5, 1.5
exp σgc	2.09, 2.70	1.9, 2.7	1.96	2.5, 3.0	1.35, 2.01

Therefore, nonspherical dust particles, as well as aerosol particles with an effective radius above 5.1 μm, are not considered. Smoke particles are captured if the (ambient) refractive index is less than 1.65, and the (ambient) imaginary part is less than 0.03. Since the Mie code is run on the fly, MAPP retrieves aerosol optical depth and aerosol microphysical parameters directly. We found it useful to preserve a gap in the effective radius [22–24] between 0.51 to 0.626 μm for the fine and coarse modes to reduce cross-talk in the retrieval.

Comparisons with the MODIS SeaDAS aerosol model

The SeaDAS aerosol model [23] currently being used in the atmospheric correction for MODIS/SeaWiFS ocean color retrievals parameterizes the particle size of the coarse and fine modes, the real refractive index and single-scattering albedo, to vary with relative humidity. For example, at a relative humidity of 70% or RH = 0.7, r_vf = 0.158 μm and r_vc = 2.927 μm. The standard deviations for both modes are kept fixed at all relative humidities: σ_gf = 0.437, corresponding to an effective variance of v_eff,f = 0.21; and σ_gc = 0.672, corresponding to an effective variance of v_eff,c = 0.57. For the atmospheric correction, one of 10 possible fine mode fractions in volume-density, f_v, can be retrieved: 0, 0.01, 0.02, 0.05, 0.10, 0.20, 0.30, 0.50, 0.80, 0.95. Compared to using the SeaDAS aerosol model to retrieve a 3-parameter set of {RH, τ_f, τ_c}, MAPP retrieves the 2 optical depths {τ_f, τ_c} and directly retrieves 6 aerosol microphysical parameters: {r_nf, r_nc, n_rf, n_if, σ_gf, σ_gc}.

C. Ocean model

The ocean surface roughness is modeled by a one-dimensional Gaussian (Cox-Munk) distribution of surface slopes, parameterized by wind speed [25]. The underwater scattering and absorption properties are described by the one-parameter Chowdhary polarized ocean bio-optical model (C2012, C2006) [6, 7], which is parameterized by the chlorophyll concentration, CHL [mg/m³]. The one-parameter C2012 model was originally designed for chlorophyll concentrations 0 ≤ CHL ≤ 3 [mg/m³], but we found it useful to allow chlorophyll concentrations up to 10 mg/m³ in order to represent more productive waters. Results from inversions of RSP polarimeter data collected during the SABOR campaign demonstrated the limitations of the original model and the improvement resulting from its extension to CHL values as large as 10 [mg/m³]. These results are presented in section 6. The C2012 model is summarized in Appendix A.

D. Vector radiative transfer model

The vector radiative transfer code we used is based on doubling-adding principles first proposed by H.C. van de Hulst (1963) [26] and developed starting in the late 1960s by James Hansen and Joop W. Hovenier [17, 27–29] and has been continuously upgraded [30, 31]. Adding refers to combining two inhomogeneous layers while doubling refers to combining two homogenous layers. Full polarization is available (all 4 Stokes parameters). The solution to the vector radiative transfer equation is given by the following recipe:

$${\mathbf{Q}}_1={\mathbf{R}}_a^{\ast }{\mathbf{R}}_b^{\ast },$$ (11a)

$${\mathbf{Q}}_n={\mathbf{Q}}_1{\mathbf{Q}}_{n-1},$$ (11b)

$$\mathbf{S}=\sum _{n=1}^{\infty }{\mathbf{Q}}_n,$$ (11c)

$$\mathbf{U}={\mathbf{R}}_b{e}^{-{\tau }_a/{\mu }_0}+{\mathbf{R}}_b\mathbf{D},$$ (11d)

$$\mathbf{D}={\mathbf{T}}_a+\mathbf{S}{e}^{-{\tau }_a/{\mu }_0}+\mathbf{S}{\mathbf{T}}_a,$$ (11e)

$$\mathbf{R}\left({\tau }_a+{\tau }_b\right)={\mathbf{R}}_a+e^{-{\tau }_a/\mu }\mathbf{U}+{\mathbf{T}}_a^{\ast }\mathbf{U},$$ (11f)

$$\mathbf{T}\left({\tau }_a+{\tau }_b\right)=e^{-{\tau }_b/\mu }\mathbf{D}+{\mathbf{T}}_b{e}^{-{\tau }_a/{\mu }_0}+{\mathbf{T}}_b\mathbf{D}.$$ (11g)

τ_a is the optical thickness of the first layer, and τ_b is the optical thickness of the second layer. The exponential terms represent direct beam attenuation at solar zenith cosine μ₀ while T is the diffuse transmission matrix. The bold-faced uppercase letters are 4 × 4 matrices that represent diffuse scattering matrices, the reflection matrix, R, the transmission matrix, T, and the downwelling and upwelling (D and U) matrices between the two layers. By multiplying the above reflection, transmission, upwelling, and downwelling matrices by the incident beam flux πμ₀ f₀, and by including the direct beam exponential term, we can find the Stokes vector components representing the reflection at the top, μ₀πf₀R, the transmission at the bottom, ${\mu }_0\pi f_0\mathbf{\text{T}}\left({\tau }_a+{\tau }_b\right)+{\mu }_0\pi f_0{e}^{-\left({\tau }_a+{\tau }_b\right){\mu }_0}$, and the downwelling and upwelling $\left({\mu }_0\pi f_0\mathbf{D}\text{and}{\mu }_0\pi f_0\mathbf{U}\right)$ between the two layers. The superscript * denotes reflection (or transmission) matrices when illuminated from below, and for homogenous layers, ${\mathbf{R}}^{\ast }\left(\mu ,{\mu }_0,\text{Δ}\varphi \right)={\mathbf{R}}^{\ast }\left(\mu ,{\mu }_0,-\text{Δ}\varphi \right)$, where μ is the polar angle cosine and Δϕ = ϕ − ϕ₀ is the difference between the azimuthal angle ϕ and the azimuthal solar angle ϕ₀.

3. OPTIMAL ESTIMATION

To test the MAPP algorithm, we generated simulated data for the seven RSP window channels at λ = 410, 469, 555, 670, 864, 1594, and 2264 nm, and added noise as discussed in 4B. The complete list of RSP channels is described in section 4A. The 960 nm channel to determine the water vapor absorption using Eq. (3).

The cost function is defined as [32]

$$\begin{array}{l}{\chi }^2(\mathbf{x})=\text{Φ}(\mathbf{x})\\ =\text{Φ}{(\mathbf{x})}_{\text{data}}+\text{Φ}{(\mathbf{x})}_{\text{prior}}\\ =\frac{1}{2}{(f-\mathbf{y})}^T{\mathbf{S}}_{ϵ}^{-1}(f-\mathbf{y})+\frac{1}{2}{\left(\mathbf{x}-{\mathbf{x}}_a\right)}^T{\mathbf{S}}_a^{-1}\left(\mathbf{x}-{\mathbf{x}}_a\right).\end{array}$$ (12)

The vector radiative transfer model, described in section 2D, is our forward model, providing the polarized radiances f, which are a function of the state vector x, Eq. (1), and which provide a suitable model for the measured polarized radiances y (either real measurements from RSP or synthetic measurements generated by the forward model with noise added). The first term may be called the data term since it depends on residuals of the forward model and the measurement, taking into account measurement error through its covariance matrix ${\mathbf{S}}_{ϵ}$. The second term may be considered the a priori term since it is the departure of the state vector x from the a priori state vector x_a, with a priori uncertainty provided by the covariance matrix S_a. The a priori state vector and covariance matrices for our problem are defined below. It is convenient to define the normalized cost function of the data term by dividing by the number of measurements, m:

$$\begin{array}{l}{\chi }^{\prime }=\frac{1}{m}\sqrt{\text{Φ}{(\mathbf{x})}_{\text{data}}}\\ =\frac{1}{m}\sqrt{\frac{1}{2}{(f-\mathbf{y})}^T{\mathbf{S}}_{ϵ}^{-1}(f-\mathbf{y})}.\end{array}$$ (13)

Generally speaking for a successful retrieval, $\frac{1}{m}\sqrt{\text{Φ}(\mathbf{x})}<1$, and if there happen to be redundant measurements then $\frac{1}{m}\sqrt{\text{Φ}(\mathbf{x})}\ll 1$. For inversions of real RSP data in this paper, we consider retrievals successful if χ′ < 0.1.

The optimal estimation method used in this paper follows a method which has been used for inverting atmospheric temperature and water vapor vertical profiles, cloud, and surface properties from hyperspectral infrared sounders [33]. It was found to be reliable and efficient in terms of the number of forward model evaluations required. The inversion results from real and simulated data presented in this paper used this method. The state vector x is transformed into fifth-root-space x₁ to smooth changes in the state parameters, analogous to a transformation into log-space:

$${\mathbf{x}}_{\mathbf{1}}={\mathbf{x}}^{1/5}.$$ (14)

In order to ensure that the state vector does not go out-of-bounds (described by x^low and x^high using the ranges in Eq. (2)) the following transformation to b-space is used:

$$\mathbf{b}=\log \frac{{\mathbf{x}}_1-{\mathbf{x}}_1^{\text{low}}}{{\mathbf{x}}_1^{\text{high}}-{\mathbf{x}}_1}.$$ (15)

If x is out-of-bounds the argument of the log will be negative, and will evaluate to an imaginary number. In order to transform from b-space to x₁-space we can use the transformation:

$${\mathbf{x}}_1=\frac{{\mathbf{x}}_1^{\text{high}}}{1+e^{-\mathbf{b}}}+\frac{{\mathbf{x}}_1^{\text{low}}}{1+e^{\mathbf{b}}}.$$ (16)

Then x is given by x = x₁⁵. The retrieval is performed in b-space. Therefore by definition, x₁ ∈ ${ℝ}^{+}$, and thus x will also be positive and real-valued. The m × n Jacobian matrix $\mathbf{K}\equiv \frac{\partial }{\partial \mathbf{x}}f$ is expressed in b-space by:

$${\mathbf{K}}_{\mathbf{b}}=\frac{df}{d\mathbf{b}}=\frac{d\mathbf{x}}{d\mathbf{b}}\frac{df}{d\mathbf{x}}=\frac{d\mathbf{x}}{d\mathbf{b}}\mathbf{K}=\frac{d\mathbf{x}}{d{\mathbf{x}}_1}\frac{d{\mathbf{x}}_1}{d\mathbf{b}}\mathbf{K}.$$ (17)

The scaled cost function is a scalar value ${\chi }_s^2$ defined by:

$${\chi }_s^2=\frac{1}{2}{(f-\mathbf{y})}^T{\mathbf{S}}_{ϵ}^{-1}(f-\mathbf{y})+\frac{1}{2}{(\mathbf{b}-{\mathbf{b}}_a)}^T{\mathbf{S}}_{1a}^{-1}(\mathbf{b}-{\mathbf{b}}_a)$$ (18)

where b_a is the a priori state vector in b-space and S_1a is the a priori covariance in b-space proportional to the Jacobian. The following iteration over i is performed until x₁ converges:

$${\mathbf{b}}_{i+1}={\mathbf{b}}_a+{\mathbf{S}}_i\left[(f-\mathbf{y})+{\mathbf{K}}_{\mathbf{b}}\left({\mathbf{b}}_i-{\mathbf{b}}_a\right)\right]$$ (19)

where S_i is the iteration-dependent a priori term [33].

We used a conservative and simple way to specify the a priori state vector, x_a, using the mean of the allowable range of each retrieval parameter, and which is also used as the first guess x_i:

$${\mathbf{x}}_a=\left({\mathbf{x}}_{\text{low}}+{\mathbf{x}}_{\text{high}}\right)/2\equiv {\mathbf{x}}_i.$$ (20)

The a priori covariance matrix, defined as a diagonal matrix, is given by

$${\mathbf{S}}_a=\text{diag}\left({\overrightarrow{\sigma }}_a\circ {\overrightarrow{\sigma }}_a\right),$$ (21)

where ${\overrightarrow{\sigma }}_a$ is a vector representing the standard deviations of the a priori values, which represent 1σ uncertainties, and is set equal to the a priori state vector, so that ${\overrightarrow{\sigma }}_a={\mathbf{x}}_a$ and ${\overrightarrow{\sigma }}_a\circ {\overrightarrow{\sigma }}_a$ denotes the Schur product.¹ The measurement error covariance matrix ${\mathbf{S}}_{ϵ}$ is given in section 4B.

Once the retrieval has converged to $\widehat{\mathbf{x}}$, we calculate the posterior covariance matrix at $\widehat{\mathbf{x}}$, or the state error covariance matrix, given by

$${\widehat{\mathbf{S}}}^{-1}(\widehat{\mathbf{x}})=\mathbf{K}{(\widehat{\mathbf{x}})}^T{\mathbf{S}}_{ϵ}^{-1}\mathbf{K}(\widehat{\mathbf{x}})+{\mathbf{S}}_a^{-1}.$$ (22)

The square root of the diagonals of ${\widehat{\mathbf{S}}}^{-1}$ give the 1σ uncertainty estimates of the retrieval accuracy, and the non-diagonal elements indicate how correlated the retrieval parameters are to each other. A diagonal or nearly-diagonal ${\widehat{\mathbf{S}}}^{-1}(\widehat{\mathbf{x}})$ indicates that the retrieval parameters are orthogonal to each other, without overlapping impacts on the modeled measurements. The RSP MAPP data files with the retrievals provide the uncertainty estimates of the state vector given by Eq. (22), and the propagated uncertainty for the fine and coarse mode effective radii, effective variances, and the fine mode single-scattering albedo.

A. Desired uncertainty targets

The desired [34] one standard deviation (1σ) target accuracy for each aerosol retrieval parameter are summarized in Table 2. As the aerosol optical depth becomes small, it becomes difficult to retrieve aerosol properties.

Table 2.

Aerosol uncertainty targets for one standard deviation (1_σ). Assumption: aerosol optical depth τ_555f ≥ 0.05 and τ_555c ≥ 0.02, otherwise uncertainty targets become difficult to meet. The effective radius is a function of the mode radius r_n and the mode width σ_g (Eq. (9)). The effective variance is a function of the size distribution mode width σ_g only (Eq. (10)). The root-mean-square deviation (RMSD) for the simulated retrievals presented in this paper are provided in the fourth column.

Param.	Description	1σ desired uncertainty	RMSD (simulated)
τ555f	fine mode optical depth at 555 nm	0.02	0.0427 (0.0372‡)
reff,f	fine mode effective radius	0.015 μm	0.0196 μm
veff,f	fine mode effective variance	0.05	0.0487
rnf	fine mode real part	0.02	0.0293
SSAf	fine mode SSA	0.02	0.0209
τ555c	coarse mode optical depth at 555 nm	0.02	0.0132
reff,c	coarse mode radius	0.15 μm	0.148 μm
veff,c	coarse mode effective variance	0.05	0.0669
CHL	chlorophyll concentration	0.7 mg/m3	2.59 mg/m3
v	windspeed	0.5 m/s	0.501 m/s

^‡RMSD vs HSRL-1 total (fine and coarse) AOD at 532 nm from SABOR.

4. MEASUREMENTS

A. Polarimeter measurements

The RSP instrument [1] is capable of measuring the I, Q, and U Stokes parameters from multiple viewing angles and at multiple wavelengths. However, for this capability to be realized the vector of aircraft motion must be parallel (or near-parallel) to the scanning direction. Data where the aircraft has substantial yaw is therefore excluded from this study. The exact nine RSP channel wavelengths, with FWHM in brackets [nm], are 410.27 [30], 469.13 [20], 554.96 [20], 670.01 [20], 863.51 [20], 960.0 [20], 1593.51 [60], 1880.0 [90], 2263.51 [120] nm, with angles measured between ±65° from zenith. These FWHM values are used to integrate the gaseous absorption in each channel assuming a rectangular response function centered at the channel wavelength (see section 2B.1 and Chen et al., 2017 [35]).

The upwelling (reflected) polarized radiances (Stokes parameters) measured in the Earth’s atmosphere are defined by:

$$\text{Total Radiance}=\frac{{\mu }_0{F}_0}{\pi d_s^2}{R}_{I,Q,U}\left[\text{W}/{\text{m}}^2/\text{sr}\right]$$ (23)

where the ratio $d_s^2={\left[\frac{\text{Earth–to–Sun distance}}{1\text{AU}}\right]}^2$ depends on day of year, μ₀ is the solar zenith angle, and F₀ is the solar irradiance at the top of the atmosphere [W/m²]. Thus the actual solar irradiance that depends on time of year is given by $F_0/d_s^2$. $R_{I,Q,U}\equiv \pi \{I,Q,U\}/{\mu }_0[1/\text{sr}]$ is the reflectance of the I, Q, or U Stokes parameter, respectively. The RSP L1B files contain measurements of calibrated normalized radiances which are defined by ($\frac{\pi }{F_0}\times$ Total Radiance):

$$\text{RSP L1B Normalized Radiance}=\frac{{\mu }_0}{d_S^2}{R}_{I,Q,U}[1/\text{sr}].$$ (24)

Therefore, the RSP measurement is related to the reflectance calculated from vector radiative transfer programs by:

$$R_{I,Q,U}=\frac{d_s^2}{{\mu }_0}(\text{RSP L1B Normalized Radiance})[1/\text{sr}].$$ (25)

To retrieve aerosol microphysical and ocean color parameters, MAPP used all seven of RSP’s window channels, and the 960 nm water vapor detection channel was used to correct the measurements for water vapor absorption, as described in section 2B. RSP also has a channel at 1880 nm for cirrus detection using water vapor absorption, but that channel was used only for cloud screening. The RSP FOV is 14 mrad corresponding to a horizontal resolution of about 100 m with measurements occurring about every 0.8 seconds corresponding to 72 revolutions per minute. The RSP measurements were horizontally averaged ± 30 seconds, or 6.6 km assuming an aircraft cruising speed of about 110 m/s, since aerosol properties would not be normally expected to vary significantly over this distance. The measurements are then mapped to the same point on the ocean surface. As a pre-processing step, a cloud mask was constructed using HSRL/RSP cloud products to screen for clouds within ± 160 seconds of a particular scene, to mitigate contamination from cloud 3D side illumination effects. Thus no RSP MAPP retrievals should have been attempted within 160 seconds of a cloud, or about 17 km, but clouds to the side of the aircraft could currently go undetected.

B. Polarimeter measurement noise

Optimal estimation fits the forward model to the measurements while accounting for measurement errors via the measurement covariance matrix ${\mathbf{S}}_{ϵ}$. The form of ${\mathbf{S}}_{ϵ}$ depends upon the measurements and the instrument calibration. If the measurements are independent then the measurements are uncorrelated and ${\mathbf{S}}_{ϵ}$ is diagonal, which is a commonly used approximation [36, 37] that is valid to first order for RSP. For all channels, RSP has an accuracy in the Stokes parameters {R_I, R_Q, R_U} of 3.5%, an accuracy of 0.2% for the degree of linear polarization, and polarization azimuth within 0.5°.

Simulated data RSP error model:

For simulated data, we assumed an error of 2% normally distributed for each Stokes parameter in the set {R_I, R_Q, R_U}. Thus for each simulated measurement {R_I, R_Q, R_U}, there is a 99.7% probability that the measurement will be found within ± 6% of the measured value. The simulated RSP measurement error covariance thus used $C_I^{\text{sim}}=C_Q^{\text{sim}}=C_U^{\text{sim}}={\left(0.02R_{I,Q,U}\right)}^2$, and which was then propagated to R_IL = (R_I + R_Q)/2, R_IR = (R_I − R_Q)/2 and the degree of linear polarization, $\text{DoLP}=\frac{\sqrt{R_Q^2+R_U^2}}{R_I}:{\mathbf{S}}_{ϵ}^{\text{sim}}\equiv C_{\text{RSP}}^{sim}=\text{diag}\left(C_{I_L}^{\text{sim}},C_{I_R}^{\text{sim}},C_{\text{DoLP}}^{\text{sim}}\right).$

Real data RSP error model:

The actual RSP measurement error covariances on R_I, R_Q, R_U, R_IL, R_IR and R_DoLP are given in Appendix B.

C. Lidar measurements

The NASA Langley airborne High Spectral Resolution Lidar (HSRL-1 and HSRL-2) beam is linearly h-polarized (i.e. horizontal or ‖) and both the h-polarized and v-polarized (i.e. vertical polarization or ⊥) components of the returned signal are measured, the latter of which provides the “depolarization” of the returned transmitted signal.

The lidar equation [2] for the measured total scattering (TS) signal [W/m²/sr] for each channel is

$$P_{TS}(r)=\frac{\text{Ψ}{C}_{TS}}{r^2}\left[{\beta }_m(r)+{\beta }_a(r)\right]e^{-2{\int }_0^r\left[{\alpha }_m\left(r^{\prime }\right)+{\alpha }_a\left(r^{\prime }\right)\right]d{r}^{\prime }},$$ (26)

where r is the distance the light has traveled, corresponding to the time when the signal traveling at speed c is measured. The two unknowns are the aerosol (particulate) backscattering coefficient β_a(r) [km⁻¹ sr⁻¹] and the aerosol extinction coefficient α_a(r′) [km⁻¹]. The molecular backscattering coefficient β_m(r) and the molecular extinction coefficient α_m(r′) depend on the (known) molecular number-density. C_TS is a system calibration constant and Ψ is the transmitter-to-receiver overlap function. High spectral resolution lidars like HSRL-1 and HSRL-2 have an additional 532-nm channel which is sensitive to only the molecular (m) backscatter and thereby provides a means to retrieve the profile of extinction [2]:

$$P_{m,532}^{\parallel }(r)=\frac{F\text{Ψ}{C}_{m,532}^{\parallel }}{r^2}{\beta }_m^{\parallel }(r)e^{-2{\int }_0^r\left[{\alpha }_m\left(r^{\prime }\right)+{\alpha }_a\left(r^{\prime }\right)\right]d{r}^{\prime }}.$$ (27)

Here F is the transmission through the iodine filter employed in the molecular channel to optically remove aerosol backscatter, and $C_{m,532}^{\parallel }$ is a system calibration constant. The iodine is kept at high temperature so that it is always in the gas phase. Then the aerosol extinction coefficient can be obtained by differentiating Eq. (27) [2]. HSRL-2 has an additional high spectral resolution channel at 355 nm. Thus HSRL-2 can measure five aerosol parameters in each vertically resolved bin: three backscatter values at 355, 532, and 1064 nm, denoted β, and two extinction values at the high spectral resolution channels, 355 and 532 nm, denoted α. These five HSRL-2 measurements (3β + 2α) allow us to make comparisons of AOD at 532 and 355 nm, the 355/532 Ångstrøm exponent, the aerosol lidar ratio at 532 and 355 nm, and can also be used to retrieve microphysical aerosol parameters directly [38]. The three HSRL-1 measurements (2β + 1α) allow us to compare AOD and the lidar ratio at 532 nm, and contain significant information about aerosol vertical distribution and type. In 2012, HSRL-1 completed upgrades to make underwater measurements of the diffuse attenuation coefficient, K_d, and the hemispherical backscatter coefficient, b_bp.

HSRL AOD

HSRL lidars can measure aerosol optical depth by calculating the transmittance at a point near the aircraft (r₁) and near the surface (r₂) using the molecular lidar return $P_{m,532}^{\parallel }(r)$ and the theoretical molecular lidar backscattering coefficient ${\beta }_m^{\parallel }$ at the two points [2]:

$$\text{HSRL AOD}={\tau }_{\text{HSRL}}=-\frac{1}{2}\ln \frac{T\left(r_2\right)}{T\left(r_1\right)}=-\frac{1}{2}\ln \frac{r_2^2{P}_{m,532}^{\parallel }\left(r_2\right){\beta }_m^{\parallel }\left(r_1\right)}{r_1^2{P}_{m,532}^{\parallel }\left(r_1\right){\beta }_m^{\parallel }\left(r_2\right)}.$$ (28)

HSRL column-averaged intensive and extensive parameters

The HSRL intensive parameters, such as the lidar ratio [sr] and the lidar aerosol depolarization ratio (in the single-scattering limit) do not depend on aerosol concentration, but only the aerosol scattering and absorption cross sections [39]. By contrast, extensive parameters, such as the aerosol backscatter [1/km/sr] and aerosol extinction km⁻¹, depend on the aerosol concentration. Note that both lidar intensive and extensive parameters are inherent optical properties, since they depend on the aerosol concentration and cross sections, but not on the light field itself. We found it useful to compare the HSRL “column-averaged” lidar ratio $\langle S_a\rangle$ and Ångstrøm exponent at 355/532 (available on HSRL-2) to the RSP MAPP retrieved column-average values of lidar ratio and Ångstrøm exponent. The HSRL “column-averaged” lidar ratio is calculated as follows:

$$\langle S_a\rangle =\frac{{\sum }_{i=0}^N{\alpha }_i}{{\sum }_{i=0}^N{\beta }_i}[\text{sr}]$$ (29)

where i = 0 corresponds to the lidar measurement bin closest to the surface (≈ 0.15 km), and i = N corresponds to the bin closest to the aircraft, and Δz_i is the height interval of each lidar bin [km]. To compute $\langle S_a\rangle$, both extinction and backscatter need to be defined and on the same resolution.

MAPP aerosol top height and lidar parameter mixing rules

The aerosol top height, h_t, is defined as the height at which:

$${\int }_0^{h_t}\alpha dz=0.95{\int }_0^h\alpha dz\text{or}{\int }_0^{h_t}\beta dz=0.95{\int }_0^h\beta dz.$$ (30)

This definition of aerosol top height has the advantage of being simple and powerful, although complex, multi-layered aerosol scenes may require a more sophisticated approach.

The corresponding RSP MAPP column-averaged values for backscattering and extinction coefficients and lidar ratio were calculated using the same equations for each mode separately. Since the MAPP retrieval assumes the aerosols to be distributed homogeneously between the surface h = 0 and the aerosol top height h = h_t, the integration is from 0 to h_t, and the backscattering and extinction coefficients are assumed to be constant with height. Thus we have $\langle \beta \rangle =\beta ,\langle \alpha \rangle =\alpha ,\langle S_a\rangle =\frac{\alpha }{\beta }$ for each aerosol mode, fine and coarse. The following mixing rules are applied to calculate the RSP estimate of the column lidar ratio, which is the ratio of the total extinction to the total backscatter:

$$\langle \beta \rangle =\langle {\beta }_f\rangle +\langle {\beta }_c\rangle ,{\beta }_{fc}=\frac{{\tau }_{fc}}{h_t}{\omega }_{fc}\frac{p_{180;fc}}{4\pi },$$ (31)

$$\langle \alpha \rangle =\langle {\alpha }_f\rangle +\langle {\alpha }_c\rangle ,{\alpha }_{fc}={\tau }_{fc}/h_t,$$ (32)

$$\langle S_a\rangle =\frac{\langle {\alpha }_f\rangle +\langle {\alpha }_c\rangle }{\langle {\beta }_f\rangle +\langle {\beta }_c\rangle },$$ (33)

where the backscattering and extinction coefficients are defined for both aerosol modes by choosing f or c for fine or coarse. τ denotes the aerosol optical depth, h_t denotes the aerosol layer height, ω denotes the aerosol single-scattering albedo, and p₁₈₀ denotes the aerosol phase function at 180°.

HSRL ocean products

The HSRL-1 instrument was upgraded [40] with detectors that quickly recover from the strong Fresnel surface reflection and detect the underwater signal [41]. The lidar beam diffuse attenuation coefficient, K_beam, is measured along the direction of the lidar beam by using the molecular backscatter channel, normalized to the molecular signal directly above the water. The slope of the molecular backscatter channel with depth, z, is directly related to the diffuse attenuation coefficient [40, 42]:

$$K_d(z)=\frac{K_{\text{beam}}(z)}{\cos {\theta }_{\text{lidar,ocn}}}=-\frac{1}{2}\frac{d\ln \left[P_{m,532}^{\parallel }(r)r^2\right]}{dz}\left[{\text{m}}^{-1}\right]$$ (34)

where r = H + z/n, H is the distance from the aircraft to the ocean surface and n is the refractive index of water. The ratio of the particulate to molecular backscatter is then related to β_p, the ocean particulate backscattering coefficient at 180° ([42], [40]):

$${\beta }_p(z)={\beta }_w\left[\frac{P_{a,532}^{\parallel }(z)+P_{a,532}^{\perp }(z)}{p_{m,532}^{\parallel }(z)+P_{m,532}^{\perp }(z)}\right]\left[m^{-1}{\text{sr}}^{-1}\right]$$ (35)

where β_w is the theoretical value of the backscattering coefficient for water at 180° [43], and the four terms inside the brackets are the measured signals in the 532 nm channel as indicated. The ocean particulate backscatter is related to the hemispherical backscattering coefficient, b_bp through use of a factor χ_p,180 [sr], which represents the average of the 180° backscattering coefficient to the integral over the backward hemisphere, i.e. the integral in Eq. (43) can be approximated by

$$\frac{q_{\text{p}}}{2\pi }={\int }_{\pi /2}^{\pi }\frac{F_{\text{p}}(\text{Θ})}{4\pi }\sin \text{Θ}d\text{Θ}\cong {\chi }_{\text{p},180}{F}_{\text{p}}\left(\text{Θ}={180}^{\circ }\right)[\text{unitless}].$$ (36)

where q_p is the hemispherical particulate backscattering ratio. It has been found empirically that setting ${\chi }_{\text{p},180}=\frac{1}{2}\text{sr}$ yields good agreement with in situ measurements of b_bp ([42], [40]) so that

$$b_{\text{bp}}(z)=b_{\text{p}}{q}_{\text{p}}=b_{\text{p}}2\pi \left[{\chi }_{\text{p},180}{F}_{\text{p}}\left(\text{Θ}={180}^{\circ }\right)\right]=\pi (1\text{sr})\cdot {\beta }_{\text{p}}(z)\left[{\text{m}}^{-1}\right]$$ (37)

using the definition of the lidar particulate backscatter coefficient, ${\beta }_{\text{p}}=b_{\text{p}}{F}_{\text{p}}\left(\text{Θ}={180}^{\circ }\right)$. Thus setting ${\chi }_{\text{p},180}=\frac{1}{2}\text{sr}$ assumes that the integral of the phase function over the backward hemisphere is half the phase function at 180°. In order to compare to RSP ocean color retrievals, we define ocean column-averaged values:

$$\langle K_d\rangle =\frac{1}{h}{\int }_{z=6}^{z=17}{K}_{d}dz\text{and}\langle b_{\text{bp}}\rangle =\frac{1}{h}{\int }_{z=6}^{z=17}{b}_{\text{bp}}dz\left[{\text{m}}^{-1}\right]$$ (38)

where the limits of 6 m to 17 m were determined by a desire to avoid the near-surface measurements which can have artifacts, and to average over at least two thirds of an optical depth of lidar measurements in the water.

5. SIMULATED RESULTS

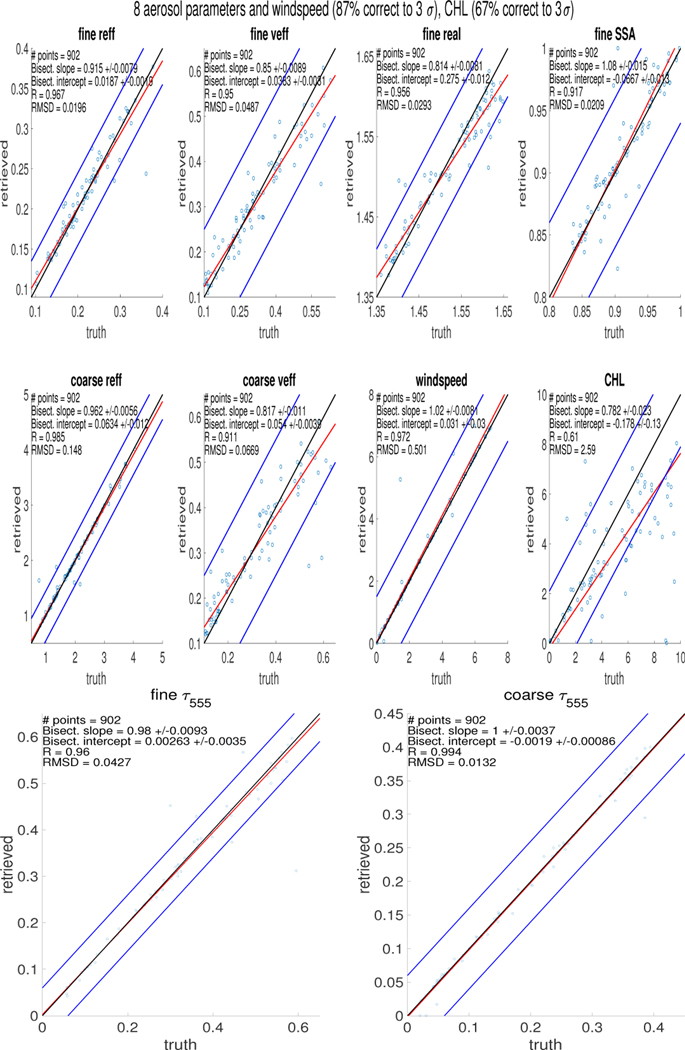
Simulations were performed using the 10-parameter state vector defined by Eq. (1) and the MAPP retrieved results using a simulated dataset are depicted in Fig. (1). The truth values were selected by using a random uniform distribution to select each retrieval parameter, independently. The ranges for the 10 parameters are given by Eq. (2). The aerosols were distributed homogeneously in a single layer between [0, 4 km]. The sensor geometry was fixed to a solar cosine zenith angle of 0.936 and relative azimuth of 105.27°. For each scene of simulated data, we randomly added Gaussian noise (one standard deviation = 2% of signal) to the Stokes parameters {R_I, R_IQ, R_U} and propagated the noise to the set of Stokes parameters {R_IL, R_IR, DoLP}. The simulated retrieval then used all seven RSP window channels simultaneously using the set {R_IL, R_IR, DoLP} and the optimal estimation method described in section 3.

Fig. 1.

Simulated retrievals using 10-parameter state space. The two lines surrounding the 1-to-1 line represent ± 3σ, or three standard deviations. The red line represents the least squares bisector. The units are μm for effective radius, m/s for wind speed and mg/m³ for chlorophyll concentration: the optical depth, effective variance, real refractive index, and single-scattering albedo are unitless. The ranges for the retrieval parameters used in this simulated study are slightly different than the finalized ranges defined by Eq. (2) for real data, but illustrate that the algorithm can successfully retrieve the 8 aerosol and windspeed parameters in 87% of the cases, and chlorophyll concentration in 67% of the cases, using simulated data where all 10 parameters are randomized.

For the simulated study, 1024 scenes were randomly constructed, and then the retrieval was performed on each of them. Out of the 1024 scenes, 902 fit the criteria where τ_555f ≥ 0.05 and τ_555c ≥ 0.02. Of these retrievals, 87% of the scenes were successful in that the 8 retrieved aerosol and windspeed parameters were all within 3σ (relative to the 1σ uncertainty goals listed in Table 2) of the true values. And 67% of the cases successfully retrieved chlorophyll concentration to 3σ, or 2.1 mg/m³. Note that for some scenes we would not expect to be able to retrieve all 10 parameters within 3 standard deviations (for example, it is difficult to retrieve coarse mode aerosol properties when the coarse mode optical depth is small, especially if the fine mode optical depth is large.)

6. RESULTS FROM SABOR JULY 31, 2014

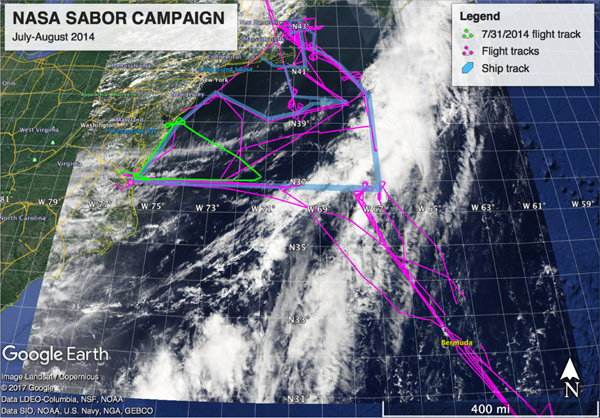
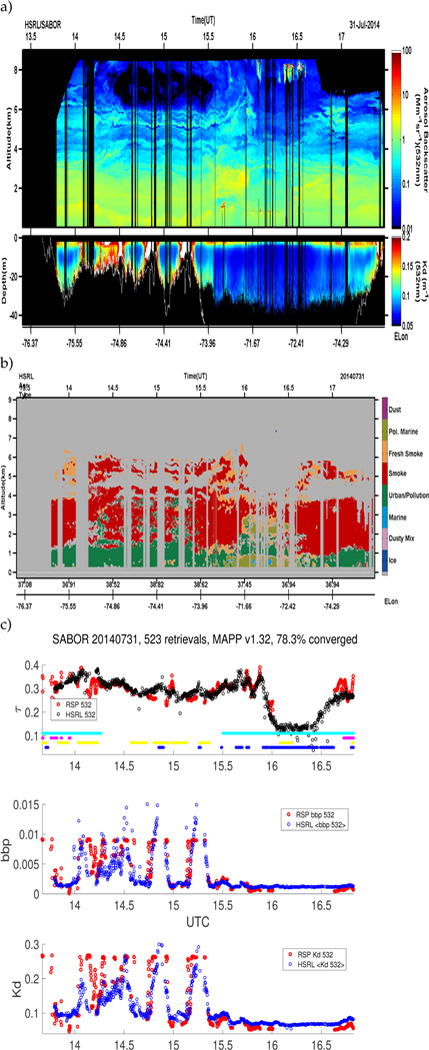
In this section we present the results from SABOR 7/31/2014, which included both shallow (less than 30 m ocean depth) and deep water ocean measurements, and the flight track is shown in green in Fig. 2 together with the MODIS Aqua true color image. The other flight tracks and the ship track are also shown for reference. The HSRL extinction and aerosol typing for this day are given in Fig. (3a) and Fig. (3b), respectively. The resulting RSP MAPP retrievals of aerosol optical depth, τ, b_bp, and K_d, are depicted in Fig. (3c). There was heavy cirrus reported as the aircraft ascended until its cruising altitude at around 14 UTC, and became thinner, broken cirrus from 14.03 UTC onwards, with clear skies reported at 14.52 UTC. The influence of the cirrus (which could also be super-cooled liquid water droplets or mixed-phase cloud) appears to erroneously increase the aerosol optical depth. For this day, and the TCAP case presented in the next section, all successful retrievals based on the magnitude of the cost function are displayed, without the altitude mask or clouds-above-aircraft mask used for the correlation plots. To help illustrate possible factors for discrepancies, the following masks are also displayed: clouds-above-aircraft (cyan), aircraft not at cruising altitude (magenta), aircraft turns/course corrections (yellow), and clouds below the aircraft (blue). According to the flight logs there should have been clear sky conditions without significant clouds above the aircraft, as indicated by the lack of a cyan mask in Fig. (3c). The variability of the ocean color measurements on this day, in addition to the complex, absorbing aerosols, make it a challenging and interesting case to study. Over the ocean, there was a tiny cloud spotted at 15:29 UTC below the aircraft, and a few small, low level cumulus clouds were detected at around 15:38 through 15:42 UTC, followed by tiny, rogue clouds sprinkled here and there. Starting at around 16:02 UTC, the aircraft flew into a low level field of cumulus clouds, and it can be seen that the AOD begins to drop significantly, and the aerosol type changes from predominantly smoke to polluted marine. (Where clouds are detected by the cloud mask based on the HSRL-1 and RSP products, RSP MAPP retrievals were not attempted.) There were also some very thin clouds near the aircraft at around 16:03 and 16:06 UTC. Another thin cloud near the aircraft which grew thicker started at 16:20 through 16:28 UTC, with the aircraft brocken spectre and surrounding glory are clearly visible in the aircraft’s nadir camera, followed by another thin cloud at 16:29 through 16:34 UTC. The RSP retrievals for these thin, opaque clouds show optical depths between 1 and 3 with droplet sizes of 5 μm or smaller [44], and the cloud top is at 8 km so they are significantly supercooled.

Fig. 2.

Overview of the NASA 2014 SABOR campaign. The ship track is highlighted in blue, and the flight tracks are highlighted in magenta. The 7/31/2014 flight track is highlighted in green, together with the superimposed MODIS Aqua true color reflectance.

Fig. 3.

SABOR July 31, 2014 flight. a) HSRL-1 atmosphere backscattering coefficient and ocean diffuse attenuation coefficient. b) HSRL-1 aerosol typing algorithm, where we can see that the aerosol structure for this day is complex with multiple layers and a lofted smoke plume. c) The atmosphere/ocean results from RSP MAPP and HSRL for this entire day. The following masks are also displayed, where the color indicates the presence of: clouds-above-aircraft (cyan), aircraft not at cruising altitude (magenta), aircraft turns/course corrections (yellow), and clouds below the aircraft (blue).

The atmosphere (aerosols and molecules) is responsible for the major part of the signal measured by RSP. Therefore, when the aerosol retrieval is successful, the aerosol optical depth in Fig. (3c) should match within 0.02 between RSP and HSRL, but not necessarily for all cases (see section 8 for a discussion of discrepancies, error sources and retrieval comparisons for the entire SABOR campaign). HSRL-1 can measure plankton and underwater particulate matter, but does not have the extra 355 nm channel available on HSRL-2. It is difficult to compare to the column-averaged HSRL-1 532 nm lidar ratio since the scenes on this day consisted of multi-layered aerosols.

SABOR 532 nm AOD comparison

The HSRL ocean profiling capability allows us to test whether the extended one-parameter ocean model is helpful in improving our AOD retrievals, and we can compare the RSP MAPP retrieved AOD at 555 nm to the HSRL-1 AOD at 532 nm (see Fig. (3c)) in order to validate our aerosol retrievals. We note that in most cases the agreement is within 0.02–0.04. Aerosols that happen to be near or above the airplane can explain larger RSP MAPP retrieved values compared to HSRL-1 but not smaller values.

SABOR ocean product comparison

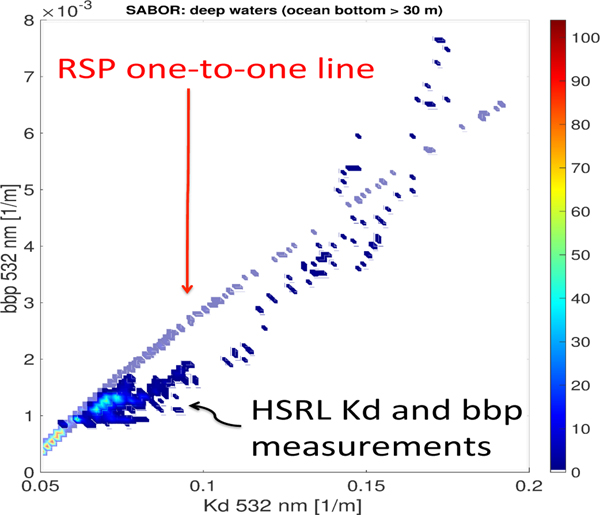
The HSRL-1 ocean measurements indicate that a significant amount of complex, coastal type water was encountered, in that K_d and b_bp do not co-vary closely with chlorophyll, i.e. they do not lie along a curve in Fig. (4), even for deeper waters (defined here as having an ocean bottom greater than 30 m). However, we can also see that a curve is not an entirely unreasonable approximation, where we have used the HSRL column-averaged values for $\langle K_d\rangle \text{and}\langle b_{\text{bp}}\rangle$ – suggesting that the one-to-one relationship between K_d and b_bp in our simplified one-parameter bio-optical model is not without merit.

Fig. 4.

RSP MAPP ocean retrievals and HSRL-1 ocean products plotted as K_d vs b_bp. The RSP C2012 ocean bio-optical model retrieval result is super-imposed against the HSRL-1 measurements HSRL-1 column-averaged $\langle K_d\rangle \text{and}\langle b_{\text{bp}}\rangle$. Only scenes for deeper waters (ocean bottom is below 30 m) are included.

Bio-optical model impact on aerosol microphysics

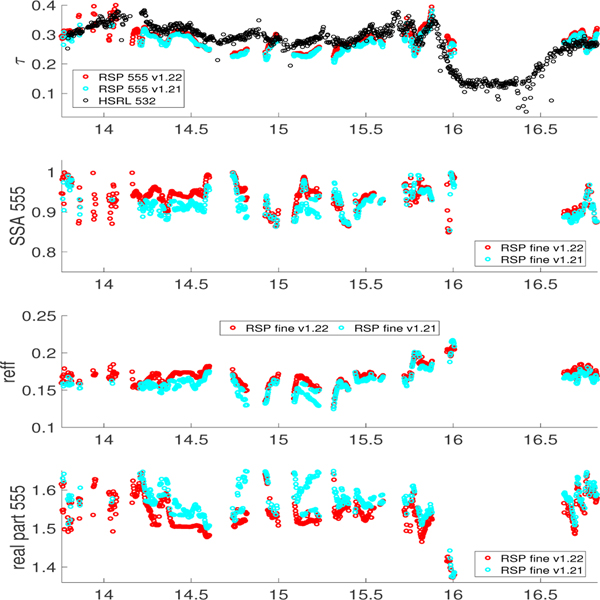
Figure (5) illustrates how the aerosol microphysics products are “coupled” to the ocean bio-optical model, since changing the bio-optical model changes the aerosol microphysics retrievals. The set of retrievals labeled “v1.21” was performed using the [0, 3] mg/m³ chlorophyll concentration ocean model (colored in cyan), while the set of retrievals labeled “v1.22” was performed using the extended [0, 10] mg/m³ ocean model (colored in red). The [0, 3] mg/m³ chlorophyll concentration saturated in high sediment/mesotrophic waters (K_d > 0.15) since this situation corresponds to the maximum allowable chlorophyll concentration value of 3.0 mg/m³. The saturation shows how bio-optical modeling errors can propagate into the aerosol retrievals (not just vice versa). We found that the extended [0, 10] mg/m³ one-parameter ocean model helped to smooth out some of the oscillations in the aerosol single-scattering albedo and real part of the refractive index, although it had less impact on the aerosol optical depth and aerosol effective radius, which tend to be easier to retrieve. Bio-optical models designed with three (or more) parameters can address the limitations in the one-parameter model, and potentially improve match-ups with the HSRL-1 ocean measurements and the quality of the aerosol microphysical retrievals.

Fig. 5.

RSP MAPP aerosol retrievals vs HSRL-1 aerosol products for a time-series of retrievals between 14 UTC and 17 UTC on 7/31/2014. From top: aerosol (a) optical depth, (b) single-scattering albedo at 555 nm, (c) (b) effective radius, (d) real part of the refractive index at 555 nm. The first set of results (v1.21) employed the one-parameter Chowdhary ocean model from 0 to 3 mg/m³ chlorophyll concentration, while the second set of results (v1.22) employed the extended range from 0 to 10 mg/m³.

7. RESULTS FROM TCAP JULY 17, 2012

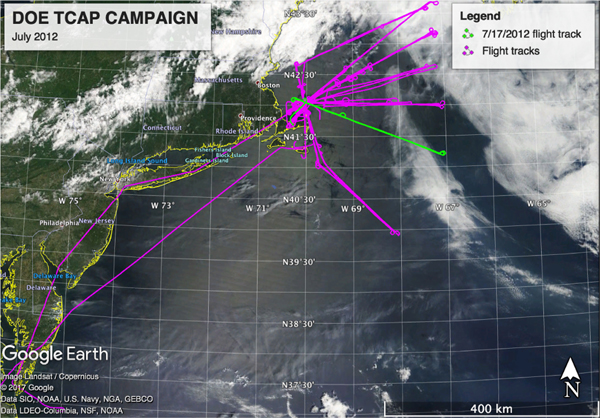
The NASA Langley HSRL-2 instrument flew together with the NASA GISS RSP during the 2012 TCAP mission. In this section we present the results from the TCAP flight on 7/17/2012, which is highlighted in green, together with the MODIS Aqua true color image, in Fig. 6.

Fig. 6.

Overview of the Department of Energy 2012 TCAP campaign. The flight tracks are highlighted in magenta. The 7/17/2012 flight track is highlighted in green, together with the superimposed MODIS Aqua true color reflectance.

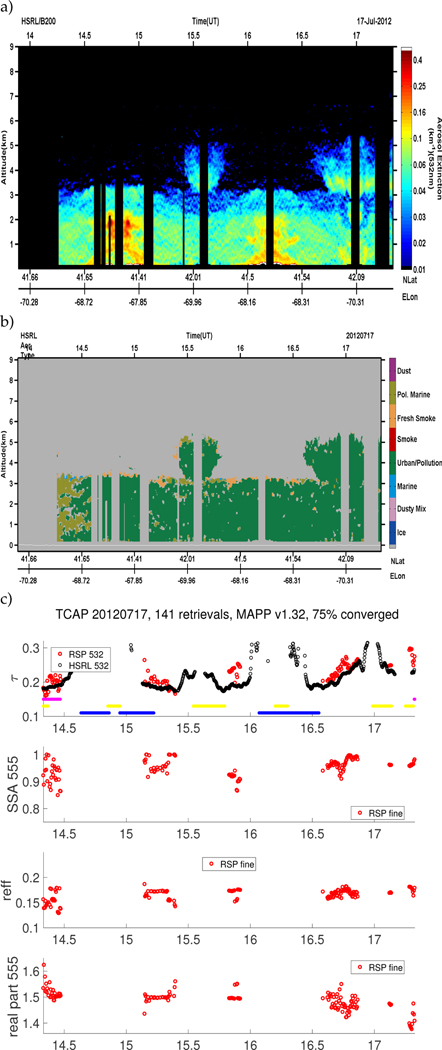
As the aircraft flew out over the ocean, and before turning point back to Cape Cod, there was a low altitude fog observed near the ocean surface at 14.75 (and again 16.25 UTC) in the RSP TCAP cloud retrievals [44], which is also apparent in the lidar backscatter in Fig. 7a. The fog had an optical depth generally between 2 and 3 with a multi-modal size distribution dominated by large drops of 10–17 μm [45] in effective radius, so it is more like a surface cloud than a classic radiation fog [46]. Above the fog, clouds at around 2 km are also apparent in the RSP cloud retrievals and in the HSRL-1 backscatter. The HSRL-1 AOD increases near the clouds, which could be due to hydrated aerosol or small cloud droplets. RSP also detected clouds near 15.5 UTC when the aircraft flew over Cape Cod as it was turning back for its return leg out over the ocean.

Fig. 7.

TCAP 07/17/2012. a) HSRL direct measurement of extinction km⁻¹ at 532 nm. b) HSRL-1 aerosol typing product. c) Atmosphere retrieval results from the RSP instrument for this entire day. RSP MAPP 532 nm aerosol optical depth and aerosol microphysics retrievals vs HSRL-2 532 nm aerosol optical depth (direct measurement) and HSRL-2 aerosol microphysics products for a time-series of retrievals between 14.5 UTC and 17.5 UTC on 7/17/2012. Aerosol products: (i) optical depth, (ii) single-scattering albedo, (iii) effective radius, (iv) real part of the refractive index. The following masks are also displayed, where the color indicates the presence of: clouds-above-aircraft (cyan), aircraft not at cruising altitude (magenta), aircraft turns/course corrections (yellow), and clouds below the aircraft (blue).

TCAP 532 nm AOD comparison

Both HSRL-1 and HSRL-2 are able to directly and accurately measure extinction km⁻¹ at 532 nm, and thus optical depth, which is extremely useful for validation and improvement of atmospheric correction algorithms for passive instruments like radiometers and polarimeters. The HSRL-2 extinction product is plotted in Fig. (7a). The HSRL aerosol typing product [39] is depicted in Fig. (7b), which uses the wavelength dependent lidar intensive parameters to discriminate between aerosol types: on this day the aerosol was characterized by a homogenous layer of urban aerosol outflow, but the plume or lofted aerosol layer overflown at 15.5 UTC and again at 17 UTC may have different properties than the aerosol below it, despite being categorized as the same type.

TCAP aerosol microphysics

In Fig. (7c), top panel, we compare the RSP MAPP retrieved aerosol optical depth at 532 nm to the HSRL-2 directly measured optical depth at 532 nm. The aerosol optical depths for this day generally agree within 0.02, despite thin cirrus (or super-cooled liquid clouds) reported above the aircraft during the beginning of the flight. In the second panel from top in Fig. (7c) we plot the aerosol RSP MAPP retrieved single-scattering albedo (SSA), which quantifies how much the aerosols absorb. Defined as the scattering coefficient divided by the extinction coefficient, an SSA value of 1.0 represents a completely non-absorbing aerosol, values close to 1 represent weakly-absorbing aerosols, while values smaller than 0.95 represent absorbing aerosols. Thus the aerosols were found to be weakly to moderately absorbing, with a retrieved aerosol SSA values between 0.9 and 1.0. Note that for a fine mode optical depth of 0.2, an SSA value of 0.95 corresponds to an aerosol absorption optical depth of 0.01, which makes it challenging to detect. The RSP MAPP retrieved aerosol effective radius (third panel from top) is about 0.15–0.17 μm for these urban aerosols. The fourth panel depicts the fine mode real part of the refractive index, which is found to vary between 1.5 and 1.6, although becoming closer to 1.4 later in the day.

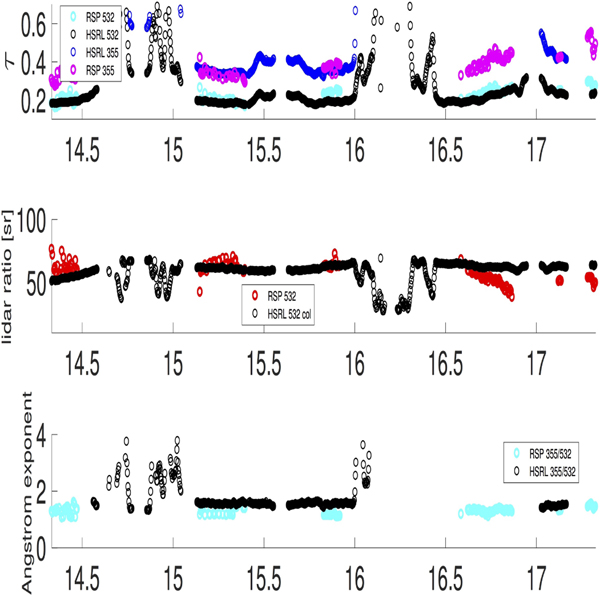
TCAP intensive/extensive product comparison

In the first panel of Fig. (8), the optical depths measured by the HSRL-2 at 355 and 532 nm are plotted, compared to the RSP MAPP retrieved aerosol product at 532 nm and 355 nm. In the second panel, the 532 nm HSRL-2 directly-measured aerosol lidar ratio, or the extinction-to-backscatter ratio, is plotted in black. The HSRL-2 column aerosol lidar ratio varies from about 50 to 70 sr on this day. The RSP MAPP retrieved lidar ratio is plotted for comparison at 555 nm (red), and at 532 nm (cyan). The RSP aerosol lidar ratio is generally within 20% of the HSRL-2 extinction-weighted aerosol lidar ratio, and although in most cases it is within 5–15 sr, it can vary up to 25 sr. Note that the polarimeter will be influenced by aerosols or ice/liquid clouds above the aircraft (see section 8 for a discussion of discrepancies, sources of error and retrieval comparisons for the entire TCAP campaign). In the third panel, the Ångstrøm exponent (355/532) measured by the HSRL-2 is compared to the RSP MAPP retrieval. We note that it is important to calculate it at 355/532 since when a size distribution is bimodal the Ångstrøm exponent can change substantially depending on which wavelength pair is used. The HSRL-2 Ångstrøm exponent is generally quite stable (1.3–1.6), while the RSP Ångstrøm exponent is generally lower (0.9–1.46), which would correspond to larger particles. Note that the HSRL-1 and HSRL-2 column aerosol lidar ratio will not include a contribution from aerosols near the surface, e.g. sea-salt aerosols in the (low) marine boundary layer, but the HSRL-2 Ångstrøm exponent represents all aerosols between the lidar and the surface.

Fig. 8.

TCAP 07/17/2012: RSP MAPP retrieved lidar intensive/extensive parameters vs HSRL-2 extinction-weighted lidar intensive/extensive parameters from top: optical depth for reference; $\langle S_a\rangle$, aerosol lidar ratio [sr] (intensive parameter); Ångstrøm exponent.

8. STATISTICAL OVERVIEW OF RESULTS AND ERROR ANALYSIS

In the following correlation plots, a clouds-above-aircraft mask was applied, and an altitude mask was applied to select only cases when the aircraft was flying a remote sensing leg at cruising altitude. For the SABOR comparisons, only the “deep water” scenes were selected, defined as having an ocean bottom of 30 m or greater, to avoid complications from ocean bottom reflectance and/or very turbid coastal waters. Although there was no instrument to specifically detect clouds above the aircraft during TCAP or SABOR, the flight logs facilitated construction of a clouds-above-aircraft mask, particularly for SABOR.

SABOR and TCAP AOD correlations

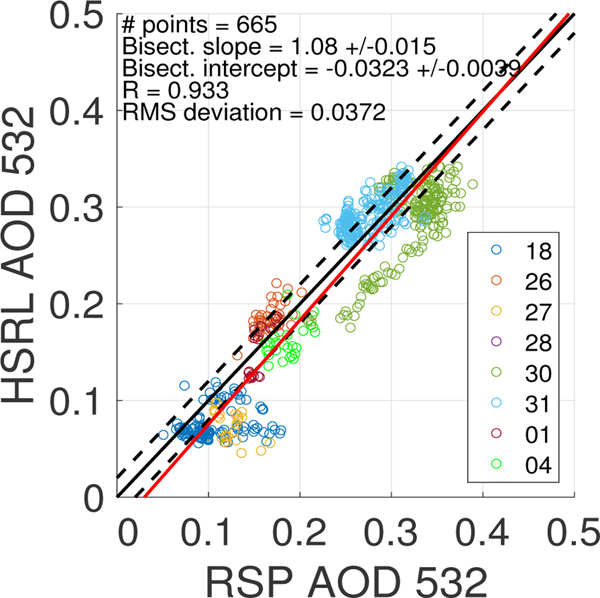
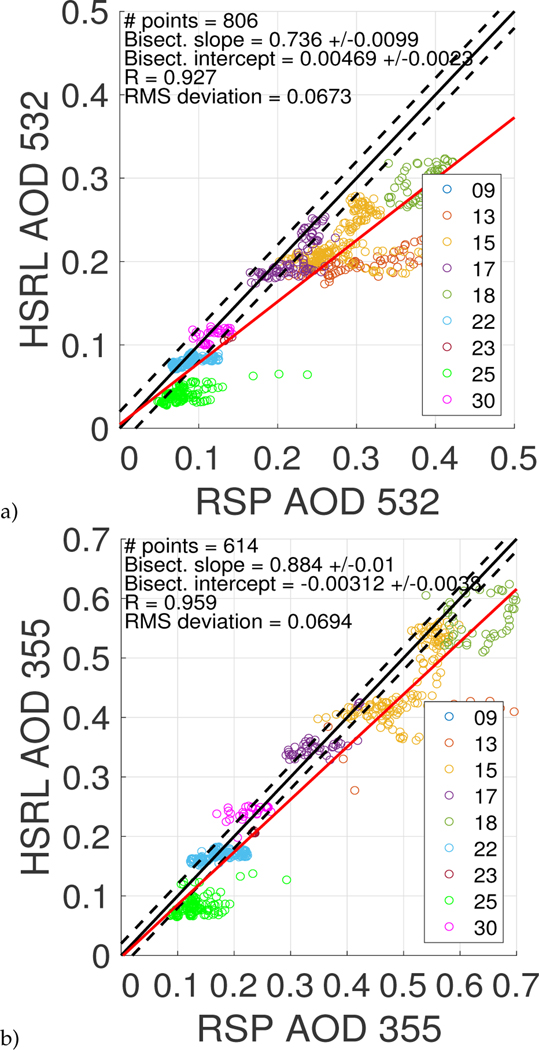
Correlations of the SABOR and TCAP Aerosol-Above-Ocean (AAO) RSP MAPP 532 nm AOD results compared to the HSRL AOD measurements are given in Figs. (9) and Fig. (10). The one-to-one line is colored in black, and the dashed black lines represent the desired ± 1σ accuracy of the RSP MAPP algorithm, which is ± 0.02 for the aerosol optical depth (AOD) at 532 nm. The HSRL-1 and HSRL-2 can measure AOD below the aircraft within ± 0.02 at 532 nm. The red line represents the least squares bisector.

Fig. 9.

SABOR campaign RSP MAPP and HSRL-1 optical depth correlations at 532 nm using HSRL AOD product after a clouds-above-aircraft mask was applied. Each color represents a different day between July 18 to August 4, 2014. The one-to-one line is colored in black, and the dashed black lines represent the desired ± 1σ accuracy. The red line represents the least squares bisector.

Fig. 10.

TCAP campaign RSP MAPP and HSRL-2 optical depth correlations using HSRL AOD product at 532 nm and 355 nm. For TCAP there was no instrument that could detect clouds above the aircraft onboard the aircraft during TCAP, and there was limited reporting of above aircraft clouds, which made clouds-above-aircraft screening difficult. Each color represents a different day in July, 2012.

The majority of RSP MAPP retrievals fall within ± 0.04 HSRL-1 or HSRL-2 AOD at 532 nm. For the SABOR campaign which had better reporting of clouds above the aircraft, of the 532 nm AOD comparisons in Fig. (9), 73% are within 0.04, 88% are within 0.06, and 98% are within 0.08, and R is 0.933 with a root-mean-square deviation of about 0.0372. For the TCAP 532 nm AOD comparisons in Fig. (10a), 53% are within 0.04, 74% are within 0.06, and 81% are within 0.08, and R is 0.927 with a root-mean-square deviation of about 0.0673.

Correlations of the TCAP RSP MAPP 355 nm AOD results compared to the HSRL-2 355 nm AOD measurements are given in Fig. (10b). The RSP MAPP retrievals are generally within ± 0.04 AOD at 355 nm (red lines), and R is 0.959 and the root-mean-square deviation of about 0.0694.

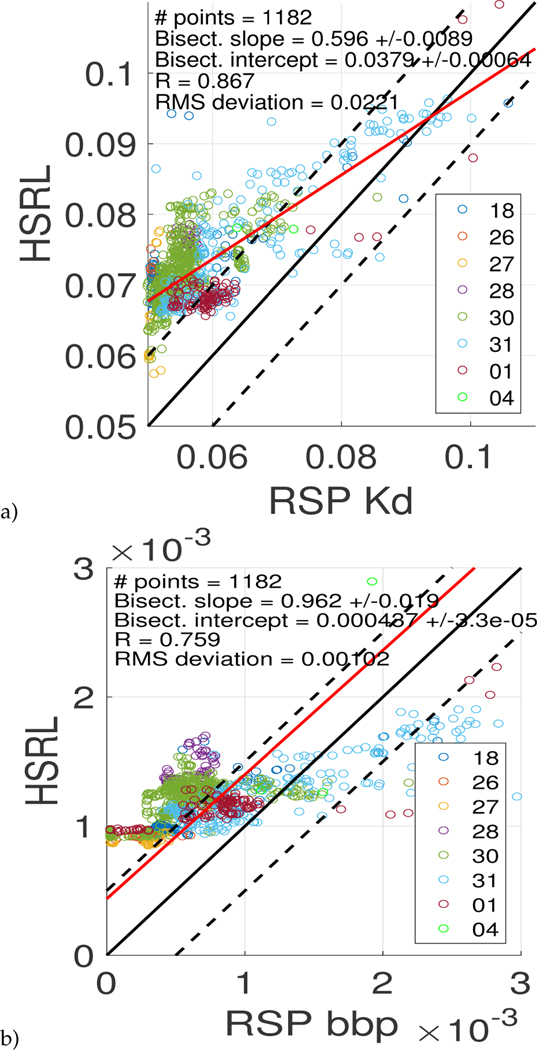
SABOR K_d and b_bp ocean product correlation

Correlations of SABOR RSP MAPP K_d and b_bp at 532 nm compared to HSRL-1 ocean measurements are given in Fig. (11). The one-to-one line is colored in black, and the dashed black lines represent the desired ± 1σ accuracy of the RSP MAPP algorithm which are ± 0.1 m⁻¹ for K_d and ± 0.0005 m⁻¹ for b_bp. The K_d root-mean-square deviation is 0.0221 and R is 0.867. At the lower limit for clearer waters, the RSP K_d is ∼ 0.05 m⁻¹ when the HSRL K_d ∼ 0.06 − 0.075, a 20% − 45% bias. At the lower limit the RSP b_bp approaches 0 m⁻¹ whereas the HSRL b_bp is 0.001 m⁻¹. At RSP MAPP retrieved b_bp values of 0.0005 m⁻¹, the HSRL b_bp generally varies between 0.001 − 0.0015 m⁻¹, which is a bias of 200% − 300%, or in absolute terms 0.0005 − 0.001 m⁻¹, which is close to the root-mean-square of about 0.000102. R for b_bp is 0.759. There is a discrepancy in K_d and b_bp for clearer waters that could be due to simplifications in the RSP MAPP ocean bio-optical model, which currently has only one parameter (chlorophyll concentration). The RSP MAPP passive ocean color retrieval uses multiple wavelengths to retrieve the bulk properties of the water assuming a single homogenous layer, whereas the HSRL measurement is at a single wavelength and is capable of providing vertical profiles in the water. We simply stress that the RSP ocean color retrieval correlates well with the average of the HSRL measurements, and therefore shows significant potential. In the future we plan to use a more advanced ocean bio-optical model to reconcile the differences at the low end (clear/oligotrophic waters) and at the high end (coastal and mesotrophic/eutrophic waters) between the ocean RSP retrieval and the HSRL measurement.

Fig. 11.

SABOR campaign RSP MAPP and HSRL-1 ocean product correlations of a) K_d [m⁻¹] and b) b_bp [m⁻¹], both at 532 nm, for all AAO (Aerosol-Above-Ocean) scenes with an ocean bottom greater than 30 m. Each color represents a different day between July 18 to August 4, 2014. The one-to-one line is colored in black, and the dashed black lines represent the desired ± 1σ accuracy. The red line represents the least squares bisector.

Active/passive discrepancies

The following conditions will lead to discrepancies between RSP passive retrievals and HSRL active measurements: i) aerosols near the aircraft, ii) aerosols within 100 m of the surface, iii) two or more layers of different aerosol types in the column, iv) lofted or multi-layered absorbing aerosols, v) non-spherical aerosols, vi) three-dimensional effects caused by clouds above or in the vicinity of the aircraft, including cloud shadowing and cloud brightening [47, 48], vii) aerosol above the aircraft, viii) cloud above the aircraft, and ix) inherent retrieval and measurement uncertainties including those for viewing geometry caused by variations in the aircraft pitch, yaw and roll, and ocean modeling errors.

The HSRL is able to detect the vertical extinction and backscatter profile of aerosols, but has larger uncertainties when aerosols are in the near field of the lidar, or if the aerosols are very close to the surface since contamination from the surface return becomes a concern (i and ii). But we note that the HSRL AOD product uses the lidar two-way transmittance to accurately measure aerosol AOD from the aircraft all the way down to the surface. The HSRL typing algorithm can potentially determine how many aerosol types are present, and the HSRL depolarization measurement can be used to identify the presence of non-spherical aerosols. Thus items iii) through vi) are largely avoidable from co-incident HSRL measurements, although three-dimensional effects from nearby clouds can be difficult to detect and will potentially require ancillary data and improved screening techniques. Aerosols and clouds above the aircraft will both hamper the algorithm’s performance, but we would not typically expect significant amounts of aerosol above the airplane. Therefore we focus on viii) liquid or ice clouds above the aircraft as a probable cause of the horizontal “streamers” in the correlation plots for RSP AOD and ix) retrieval uncertainties. For the latter, simplifications or unrealistic assumptions can cause the retrieval to diverge or converge to an erroneous solution. The current MAPP polarimeter retrieval is approximate in that it assumes that the aerosols are located in a single layer and modeled as a bimodal aerosol distribution, whereas in reality we know that aerosols can be layered in complex structures with different aerosol types. Also, the ocean bio-optical model is simplistic in that it depends on only a single parameter. The RSP vs HSRL correlation plots provide important campaign-wide aerosol and ocean product statistics, and the discrepancies indicate where the RSP MAPP retrievals can be further improved, such as enhanced aboveaircraft-cloud and nearby cloud detection and ocean bio-optical modeling.

9. CONCLUSION

A new algorithm called MAPP has been created that can invert polarimetric data to retrieve detailed aerosol microphysical parameters such as aerosol single-scattering albedo and complex refractive index, in addition to ocean color products such as the diffuse attenuation coefficient. The MAPP algorithm is fully automated, and capable of bulk processing entire field campaigns of data (thousands of scenes), and the entire framework is described in this paper. The MAPP algorithm has some unique advantages since it does not rely on look-up-tables and simultaneously retrieves aerosol and ocean products. For the first time hundreds of aerosol microphysics retrievals from the RSP polarimeter have been compared to HSRL-1/HSRL-2 AOD at multiple wavelengths, and also comparisons have been made to the HSRL-1 ocean measurements.

The MAPP algorithm was tested on simulated data, and used to analyze field data from AAO (Aerosol-Above-Ocean) scenes. These high-density retrievals from polarimeter measurements were collected during two aircraft campaigns, SABOR and TCAP. RSP MAPP retrievals were validated by comparing them to co-incident high spectral resolution lidar measurements obtained by the Langley airborne High Spectral Resolution Lidars HSRL-1 and HSRL-2. The AOD at 532 and 355 nm (when available) are compared, as are the 532-nm ocean measurements of the diffuse attenuation coefficient, K_d, and the hemispherical particulate backscattering coefficient, b_bp.

The co-incident HSRL-1/HSRL-2 measurements of AOD and column-averaged intensive parameters (lidar ratio and the Ångstrøm exponent) were useful for evaluating the MAPP algorithm, and they show significant promise as additional validation tools for atmospheric correction algorithms for passive ocean color remote sensing. We found that the HSRL aerosol optical depth at 532 nm is an extremely useful and accurate check on the aerosol retrieval, i.e. the atmospheric correction, which is important, because accurate atmospheric correction is a prerequisite for retrieval of marine parameters with reliable accuracy from passive ocean color sensors. In addition, HSRL-1’s underwater measurement capability of the diffuse attenuation coefficient, the hemispherical backscattering coefficient, and potentially the hydrosol depolarization ratio are groundbreaking measurements for evaluating polarimeter (e.g. RSP) and radiometer-retrieved (e.g. MODIS) ocean products. Taken together, these measurements have significant potential to advance the next stage of ocean color retrievals using data obtained by passive ocean color sensors. The agreement between the polarimeter and lidar observations, despite being very different measurement systems, underscores the importance of developing joint polarimeter/HSRL observations of the atmosphere/ocean system, since the two types of instruments are in many ways complementary. The RSP MAPP products are summarized on the NASA LaRC website [10] and are available for download at the NASA GISS RSP website [11].

Future work involves implementing a more advanced three- or four-parameter ocean bio-optical model into MAPP, that has for example not only a chlorophyll concentration parameter, [CHL], but also an independently varying color dissolved organic matter parameter, [CDOM], together with its spectral slope, S_CDOM, and a hemispherical backscatter parameter, [b_bp] to allow for the effects of scattering by non-algal particles. A more comprehensive ocean model would allow us to model the two-dimensional ocean complexities detected by the lidar as depicted in Fig. (4), and to potentially retrieve the CDOM and/or hemispherical backscatter wavelength-dependent slope, which can then be also compared against ship-based and buoy in situ ocean and underwater radiance-based measurements. It is also of interest to compare the MAPP aerosol retrievals to in situ measurements of aerosols made during SABOR and TCAP. We plan to add the capability to retrieve the aerosol layer height independently from RSP, since collocated lidar measurements are not always available.

Lastly, the MAPP framework was designed with the ultimate goal of being able to use HSRL-2 measurements directly in a joint polarimeter+lidar retrieval. The joint HSRL+RSP retrieval algorithm is expected to improve upon the column-averaged microphysics of the polarimeter-only version presented in this paper, while simultaneously improving the vertically-resolved microphysics retrievals of the HSRL-2-only retrievals [38, 49].

A. C2012 ONE-PARAMETER POLARIZED OCEAN BIO-OPTICAL MODEL

Scattering coefficient of the ocean

The total scattering coefficient for the ocean as a function of wavelength, λ [nm], is given by

$$b=b_{\text{sw}}(\lambda )+b_{\text{p}}(\lambda ,\text{CHL})\left[{\text{m}}^{-1}\right]$$ (39)

where the scattering coefficient for seawater, b_sw, is given by SB1981 [50]. The scattering coefficient, b_p, for the ocean particles is given by (Morel and Maritorena (MM2001) [51], Huot (2007) [52]):

$$b_{\text{p}}(\lambda ,\text{CHL})=0.347{[\text{CHL}]}^{0.766}{\left(\frac{\lambda }{660}\right)}^k\left[{\text{m}}^{-1}\right]$$ (40)

where the chlorophyll concentration, CHL [mg/m³], and k is given by (MM2001):

$$k=\{\begin{array}{ll}-1& 0\le \text{CHL}<0.02,\\ 0.5\left({\log }_{10}[\text{CHL}]-0.3\right)& 0.02\le \text{CHL}\le 2,\\ 0& \text{CHL}>2.\end{array}$$ (41)

The hemispherical backscattering coefficient b_bp ≡ b_pq_p for ocean particles, is parameterized as [51]

$$b_{\text{bp}}(\lambda ,\text{CHL})=b_{\text{p}}(\lambda ,\text{CHL})q_{\text{p}}(\text{CHL})$$ (42)

where q_p is the hemispherical particulate backscattering ratio, defined as the integral over the backward hemisphere of the combined particulate scattering phase function F_p(Θ):

$$q_{\text{p}}\equiv 2\pi {\int }_{\pi /2}^{\pi }\frac{F_{\text{p}}(\text{Θ})}{4\pi }\sin \text{Θ}d\text{Θ}[\text{unitless}].$$ (43)

The normalization of F_p differs by a factor $\frac{1}{4\pi }$ to that commonly used by the ocean color community. The C2012 ocean model was constructed by constraining Eq. (43) using the following empirical relation for q_p (C2006, MM2001), which has been modified so that there is no ${\left(\frac{\lambda }{660}\right)}^k$ wavelength dependence (C2012) for the particulate backscattering ratio:

$$q_{\text{p}}(\text{CHL})\equiv \left(0.007-0.0025{\log }_{10}[\text{CHL}]\right))[\text{unitless}].$$ (44)

Thus in this model the hemispherical backscattering coefficient b_p ≡ b_p(λ, CHL) has wavelength dependence, but not the hemispherical backscattering ratio, q_p ≡ q_p(CHL). Then the particulate hemispherical backscattering coefficient becomes

$$b_{\text{bp}}(\lambda ,\text{CHL})=b_{\text{p}}(\lambda ,\text{CHL})\left(0.007-0.0025{\log }_{10}[\text{CHL}]\right))\left[{\text{m}}^{-1}\right]$$ (45)

and the total hemispherical backscattering coefficient for the ocean is then given by

$$b_{\text{b}}(\lambda ,CHL)=b_{\text{b},\text{sw}}+b_{\text{bp}}=0.5b_{\text{sw}}(\lambda )+b_{\text{bp}}(\lambda ,\text{CHL}).\left[{\text{m}}^{-1}\right]$$ (46)

Hydrosol Mie computations and scattering matrix

The ocean particles are modeled as a bimodal mixture (D-P) of detritus (D) and plankton (P) spherical particles. Each mode is assumed to have a Junge (power-law) size distribution with radii between 0.01 and 100 μm and Junge-exponents γ_det and γ_plk, respectively. The real part of the refractive indices relative to water, n_r,det and and n_r,plk are assumed to be wavelength independent. Mie computations are used to calculate the resulting scattering matrices f_det(Θ), f_plk(Θ), scattering cross-sections σ_det, σ_plk, and the backscattering ratios q_det, q_plk. The imaginary part of the refractive index is set to zero, since its impact on the backscattering ratio is negligible (C2012). Note that we use an empirical relation, Eq. (55), to determine the total D-P particle absorption and also use an empirical relation to calculate the particulate scattering coefficient from Eq. (40), so that the hydrosol particulate single-scattering albedo is

$${\omega }_{\text{p}}(\lambda ,\text{CHL})=\frac{b_{\text{p}}(\lambda ,\text{CHL})}{a_{\text{p}}(\lambda ,\text{CHL})+b_{\text{p}}(\lambda ,\text{CHL})}.$$ (47)

But the combined D-P Stokes scattering matrix is given by the Mie computed scattering cross-sections and scattering Stokes matrices:

$$f_{\text{p}}(\text{Θ})=\frac{\left(1-f_{\text{det}}\right){\sigma }_{\text{plk}}{f}_{\text{plk}}(\text{Θ})+f_{\text{det}}{\sigma }_{\text{det}}{f}_{\text{det}}(\text{Θ})}{\left(1-f_{\text{det}}\right){\sigma }_{\text{plk}}+f_{\text{det}}{\sigma }_{\text{det}}}$$ (48)

where $f_{\text{det}}=\frac{N_{\text{det}}}{N_{\text{det}}+N_{\text{plk}}}$, and N_det and N_plk are the number of detritus and plankton particles, respectively. Therefore, the hemispherical backscattering ratio due to the D-P mixture is given by (using the definition in Eq. (43) for q_det, q_plk)

$$q_{\text{p}}=\frac{\left(1-f_{\text{det}}\right){\sigma }_{\text{plk}}{q}_{\text{plk}}+f_{\text{det}}{\sigma }_{\text{det}}{q}_{\text{det}}}{\left(1-f_{\text{det}}\right){\sigma }_{\text{plk}}+f_{\text{det}}{\sigma }_{\text{det}}}.$$ (49)

For each mode, the values are determined to be (n_r,det = 1.15, γ_det = 4.4) and (n_r,plk = 1.04, γ_plk = 3.7). The detritus fraction of the D-P mixture, f_det, then depends on the chlorophyll concentration, and can be fitted by the following polynomial to within ± 0.003:

$$f_{\text{det}}(\text{CHL})=0.61-0.099{\chi }_{\text{CHL}}-0.009{\chi }_{\text{CHL}}^2$$ (50)

where ${\chi }_{\text{CHL}}={\log }_{10}\frac{\text{CHL}}{0.03}$. By using the real part of the refractive index and the Junge exponent for detritus and plankton, we can then compute the scattering cross-sections from Mie theory as σ_det = 1.388 × 10⁻⁵ μm² and σ_plk = 8.874 × 10⁻⁵ μm².

The values above were determined as follows (C2012):

1. For a given refractive index n_r, the Junge exponent γ was varied to minimize $d=\sqrt{\frac{1}{N}{\sum }_{i=1}^{N}h{\left(p_{\text{hyd}}\left({\text{Θ}}_i\right)-p_{\text{W}}\left({\text{Θ}}_i\right)\right)}^2},$ where $p=-\frac{F21(\text{Θ})}{F11(\text{Θ})},p_{\text{hyd}}$ is for the plankton or detritus, and p_w is for water using a depolarization ratio of δ = 0.09, and the scaling factor h = 4 when p_hyd ≥ 0.85 and 1 otherwise.

2. A linear fit formula was derived from the results of 1): γ_hyd = 6.63n_hyd − 3.25.

3. The minimum and maximum values, q_p,min and q_p,max, are obtained by using CHL = 0.03 and 3.0 mg/m³ in Eq. (44), respectively. Thus q_p,min = 0.01081 and q_p,max = 0.00581 for the four RSP ocean color channels at 410, 469, 555 and 670 nm.

4. Based on applying the constraint in 3), the real refractive indices are found to be n_r,det = 1.15 and n_r,plk = 1.04. Then Junge exponents γ_det = 4.4 and γ_plk = 3.7 are obtained from the fit in 2). The resulting effective radii are small, at 0.35 μm (plankton) and 0.034 μm (detritus), since the emphasis is to reproduce variations in q_p corresponding to the MM2001 bio-optical model, and smaller particles contribute more to backscattering than larger particles.

5. Using the refractive index and Junge exponent values in 4) we can calculate the scattering matrices f_det(Θ), f_plk(Θ), scattering cross sections σ_det and σ_plk and backscattering ratios q_det and q_plk.

6. The empirical relationship between q_p as a function of CHL, Eq. (44), is used with Eq. (49) given values in 5) for σ_det, σ_plk, q_det, q_plk, to provide f_det as a function of CHL (Eq. (50)). The resulting D-P scattering matrix is consistent with a wavelength-dependent Fournier-Forand phase function (C2012).

Absorption coefficient of the ocean

In order to calculate the absorption coefficient of the ocean, C2012 uses a model of the diffuse attenuation coefficient K_d(λ, CHL). The diffuse attenuation coefficient is a quasi inherent optical property defined as [53]

$$K_d=-\frac{d}{dz}\left[\ln F_v^{-}(z)\right]=-\frac{1}{F_v^{-}}\frac{d{F}_v^{-}(z)}{dz},$$ (51)

where $F_v^{-}$ is the diffuse downwelling irradiance. One may approximate K_d as follows (MM2001):

$$\begin{gathered} K_d(\lambda ,\text{CHL})\approx K_w(\lambda )+K_{\text{bio}}(\lambda ,\text{CHL}) \\ \approx \left[a_w(\lambda )+0.5b_w(\lambda )\right]+\chi (\lambda ){[\text{CHL}]}^{e(\lambda )}, \end{gathered}$$ (52)

where K_w ≈ a_w(λ) + 0.5b_w(λ) is the apparent attenuation coefficient due to pure ocean water, and a_w and b_w are the absorption [54] and scattering coefficients, respectively, from SB1981 [50]. K_bio is the apparent attenuation coefficient for all other scattering and absorbing species in the ocean, which are assumed to covary with the chlorophyll concentration [CHL]. The parameters χ(λ) and e(λ) are regression coefficients [51]. In principle, we are only allowed to add inherent optical properties, but since K_d is a quasi inherent optical property, the error resulting from the addition in Eq. (52) is assumed to be small (MM2001). The total absorption coefficient for the ocean is then given by solving the following equation for a_ocn (C2006)

$$\begin{gathered} a_{\text{ocn}}(\lambda ,\text{CHL})=K_d(\lambda ,\text{CHL})\left[1-\alpha \left(\lambda ,\text{CHL},{\theta }_0\right)\frac{b_{\text{b}}(\lambda ,\text{CHL})}{a_{\text{ocn}}}\right] \\ \times \frac{{\mu }_d\left(\lambda ,\text{CHL},{\theta }_0\right){\mu }_u}{{\mu }_d\left(\lambda ,\text{CHL},{\theta }_0\right)\alpha \left(\lambda ,\text{CHL},{\theta }_0\right)\frac{b_{\text{b}}(\lambda ,\text{CHL})}{a_{\text{ocn}}}+{\mu }_u}\left[{\text{m}}^{-1}\right] \end{gathered}$$ (53)

where μ_d(λ, CHL) and μ_u = 0.4 are the average upward and downward cosine directions, so that (suppressing the functional dependencies)

$$a_{\text{ocn}}(\lambda ,\text{CHL})=\frac{1}{2}{\mu }_d\left(K_d-\alpha b_{\text{b}}\right)\pm \frac{1}{2}\sqrt{{\mu }_d^2{\left(K_d-\frac{\alpha b_{\text{b}}}{{\mu }_u}\right)}^2-4K_d\alpha b_{\text{b}}}.$$ (54)

The quantity $\alpha \left(\lambda ,\text{CHL},{\theta }_0\right)\frac{b_{\text{b}}(\lambda ,\text{CHL})}{a_{\text{ocn}}}\equiv \frac{E_u(\lambda )}{E_d(\lambda )}$ is the ratio of the upwelling to downwelling irradiance measured just below the ocean surface, and is equal to $\alpha \left(1+\frac{b_{\text{b}}}{a_{\text{ocn}}}\right)\left(\frac{b_{\text{b}}}{a_{\text{ocn}}+b_b}\right)$ when b_b is large compared to a_ocn [55].

Since we know the absorption for pure water, we can then find the particulate absorption (by plankton and implicitly CDOM):

$$a_{\text{p}}(\lambda ,\text{CHL})=a_{\text{ocn}}(\lambda ,\text{CHL})-a_{\text{w}}(\lambda ).$$ (55)

Thus the C2012 bio-optical model depends only on chlorophyll concentration (one parameter), and is consistent with i) the commonly used Fournier-Forand phase function for scattering by plankton particles, ii) empirical measurements of scattering and absorption coefficients, and iii) provides the full 4×4 scattering matrix for polarized light calculations. The goal of a bio-optical model should be to capture the relevant changes in the inherent optical properties in the UV and visible with as few parameters as possible, and ideally to be as general and realistic as possible to allow application to as many different regions as possible. In that context, the C2012 model works well for having only a single parameter. Future work would reduce assumptions and increase the number of parameters to allow more detailed retrieval of in-water inherent optical properties.

Example C2012 IOP calculation (λ=555 nm, CHL=1 mg/m³)

From Morel and Mueller (2002) [55], α(λ, CHL, θ₀) ≈ 0.38. K_d(λ, CHL) = 0.09857 (MM2001). b_b(λ, CHL) = 0.00431 since b_b,sw(λ) = 0.0019 [50] and b_bp(λ, CHL) = 0.00236 (MM2001). At SZA = 30°, μ_d(SZA, λ, CHL) = 0.832. μ_u = 0.4 for all wavelengths and chlorophyll concentrations (MM2001). Thus a_ocn(λ, CHL) = 0.077515 m⁻¹.

B. RSP UNCERTAINTY MODEL

The actual RSP measurement error covariances are given as follows, substituting in the following values: ${\sigma }_{\text{floor}}^{\prime }=0.00002,a^{\prime }=1\times {10}^{-7},{\sigma }_{\ln K_1}=0.005(0.5\text{\%}),{\sigma }_{\ln {\alpha }_c}=0.015(1.5\text{\%}),{\sigma }_{\ln {\alpha }_1}=0.002(0.2\text{\%})$.

$$\begin{gathered} C_I={\sigma }_{R_I}^2={\left(\sqrt{2}\frac{{\sigma }_{\text{floor}}^{\prime }}{{\mu }_0}\right)}^2+{\left(\sqrt{\frac{a^{\prime }}{{\mu }_0}{R}_I}\right)}^2+{\left(\frac{R_Q}{2}{\sigma }_{\ln K_1}\right)}^2 \\ +{\left(R_I{\sigma }_{\ln {\alpha }_c}\right)}^2. \\ {C}_Q={\sigma }_{R_Q}^2={\left(\frac{{\sigma }_{\text{floor}}^{\prime }\sqrt{2}}{{\mu }_0}\right)}^2+{\left(\sqrt{\frac{a^{\prime }{R}_I}{{\mu }_0}}\right)}^2+{\left(\frac{1}{2}{R}_I{\sigma }_{\ln K_1}\right)}^2 \\ +{\left(R_Q{\sigma }_{\ln {\alpha }_c}\right)}^2+{\left(R_Q{\sigma }_{\ln {\alpha }_1}\right)}^2. \\ {C}_U={\sigma }_{R_U}^2={\left(\frac{{\sigma }_{\text{floor}}^{\prime }\sqrt{2}}{{\mu }_0}\right)}^2+{\left(\sqrt{\frac{a^{\prime }{R}_{I_2}}{{\mu }_0}}\right)}^2{\left(\frac{1}{2}{R}_{I_2}{\sigma }_{\ln K_1}\right)}^2 \\ +{\left(R_U{\sigma }_{\ln {\alpha }_c}\right)}^2+{\left(R_U{\sigma }_{\ln {\alpha }_1}\right)}^2. \\ {C}_{I_L}={\sigma }_{R_{I_L}}^2=\frac{C_I}{4}+\frac{C_Q}{4}+{\left(\frac{R_I+R_Q}{2}{\sigma }_{\ln {\alpha }_c}\right)}^2 \\ +{\left(\frac{R_I+R_Q}{4}{\sigma }_{\ln K_1}\right)}^2+{\left(\frac{R_Q}{2}{\sigma }_{\ln {\alpha }_1}\right)}^2. \\ {C}_{I_R}={\sigma }_{R_{I_R}^2}=\frac{C_I}{4}+\frac{C_Q}{4}+{\left(\frac{R_I-R_Q}{2}{\sigma }_{\ln {\alpha }_c}\right)}^2 \\ +{\left(\frac{R_I-R_Q}{4}{\sigma }_{\ln K_1}\right)}^2+{\left(\frac{R_Q}{2}{\sigma }_{\ln {\alpha }_1}\right)}^2. \\ {C}_{\text{DoLP}}={\sigma }_{\text{DoLP}}^2={\left(\sqrt{2}\frac{{\sigma }_{{\text{floor}}^{\prime }}}{{\mu }_0{R}_I}\sqrt{2+{\text{DoLP}}^2}\right)}^2 \\ +{\left(\sqrt{\frac{a^{\prime }}{{\mu }_0{R}_I}}\sqrt{2-{\text{DoLP}}^2}\right)}^2 \\ +{\left(\frac{1}{\sqrt{2}}{\sigma }_{\ln K_1}\sqrt{1-{\text{DoLP}}^2}\right)}^2+{\left({\sigma }_{\ln {\alpha }_1}\text{DoLP}\right)}^2 \\ +{\left(\frac{1}{2}{\sigma }_{\ln K_1}\frac{\sqrt{R_Q^4+R_U^4}}{R_I^2}\right)}^2. \end{gathered}$$ (56)