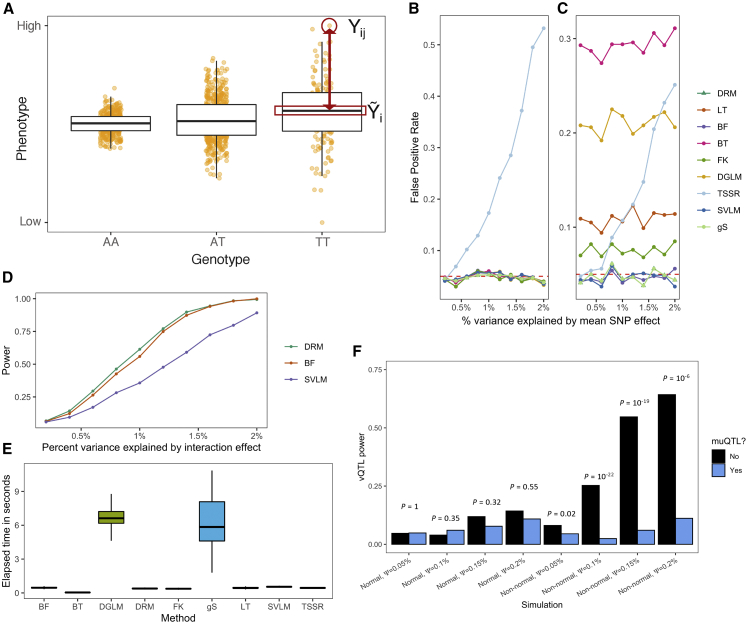
Figure 2.

Assessing a variance test for finding SNPs with interaction effects

(A) The DRM uses the absolute difference between an individual’s phenotype Y_ij (for each genotype i and individual j) (y axis) and the within-genotype phenotype median (Y_i) as a dependent variable. The absolute difference is modeled in a linear regression across genotypes (x axis). Simulated data shown.

(B and C) False positive rates for different variance tests at SNPs with varied mean effects in a (B) normal and (C) non-normal phenotype. Methods tested are as follows: DRM, Levene’s test (LT), Brown-Forsythe test (BF), Bartlett’s test (BT), Fligner-Killeen test (FK), double generalized linear model (DGLM), two-step squared residual approach (TSSR), squared value linear modeling (SVLM), and extended Levene’s test of generalized scale (gS).

(D) Power of the DRM, BF, and SVLM in non-normally distributed phenotypes. The gS method’s power is nearly identical to the DRM and is not displayed.

(E) The elapsed time to perform each method on a single SNP across 1,000 simulations. The data are summarized as boxplots where the middle line is the median, the lower and upper hinges are the first and third quartiles, and the whiskers extend from the hinge with a length of 1.5× the inter-quartile range.

(F) vQTL test power, quantified by the DRM, stratified by whether the SNPs are detected by a muQTL test (linear regression). By using a 2-by-2 contingency table representing the counts of muQTL and vQTL test rejection across 1,000 simulations, Fisher’s exact test assessed whether muQTL power and vQTL power show non-random association. p values are displayed.