Preventing epidemics by wearing masks: An application to COVID-19

Abstract

The goal of this work is to consider widespread use of face masks as a non-pharmaceutical control strategy for the COVID-19 pandemic. A SEIR model that divides the population into individuals that wear masks and those that do not is considered. After calculating the basic reproductive number by a next generation approach, a criterion for determining when an epidemic can be prevented by the use of masks only and the critical percentage of mask users for disease prevention in the population are derived. The results are then applied to real world data from the United States, Brazil and Italy.

1. Introduction

The COVID-19 crisis has created the biggest public health concerns of 2020. Since being first reported at the end of 2019, the disease has caused over 23 million confirmed cases and 800 thousand deaths by the end of August 2020 [1]. Many studies to model the pandemic spread were developed (e.g. [2], [3], [4], [5], [6]) with results influencing the policies of governments around the world.

Attempts to minimize the damage of the pandemic were then implemented, such as mandatory mask use and quarantines, which improved the overall scenario, but so far there are no drugs or vaccines to treat or immunize people and maintaining quarantines for longer time periods is not a viable option in some communities. Therefore, looking for non-pharmaceutical control strategies is essential to deal with this epidemic and others in the future.

This paper addresses this issue considering the widespread use of masks as in other works such as [7], [8], [9], [10]. If this measure is enough to avoid an epidemic outbreak, then other strategies that take bigger tolls on the economy such as quarantines would not be necessary. A SEIR model [11] with individuals divided into those that wear masks and those that do not is considered in Section 2, and its basic reproductive number is calculated by a next generation approach in Section 3. This leads to a criterion that determines when an epidemic outbreak can be avoided by mask use only, and a critical percentage of mask users in the population is derived.

For applications of these methods, we perform the parameter fitting in Section 4 with data from the United States, Brazil and Italy and analyse whether the COVID-19 crisis could have been avoided in these countries with widespread mask use from the beginning of the outbreak. In addition, numerical simulations are carried out to verify how the evolution of the disease is mitigated if it cannot be avoided. The conclusions are drawn in Section 5.

2. Model structure

Consider a population $N$ that is divided into individuals that wear masks, denoted by $N_m$ and individuals that do not, denoted by $N_n$. Let $p\left(t\right)$ be the percentage of people wearing a mask in the population at time $t\ge 0,$ then

$$N_m\left(t\right)=p\left(t\right)N\left(t\right),N_n\left(t\right)=(1-p\left(t\right))N\left(t\right).$$ (1)

Both $N_n$ and $N_m$ are also divided into four epidemiological classes, consisting of susceptible, exposed, infected and removed individuals, denoted by $S_n$ and $S_m,$ $E_n$ and $E_m,$ $I_n$ and $I_m$ and $R_n$ and $R_m,$ respectively. As the model will consider only a short time period in comparison to the demographic time frame, vital parameters will be neglected, so the total population will be assumed constant, that is,

$$N\left(t\right)=N.$$ (2)

Let $r$ be a multiplicative factor for the transmission rate $\beta$ that will take into account the reduction in the probability of contagion from one person wearing a mask in a susceptible-infected contact. We assume that this reduction is the same whether a susceptible or an infective is wearing the mask. When only one individual has a mask on, we assume that the new transmission rate is $r\beta$. In the case of both individuals with masks on, then the transmission rate is assumed to be $r^2\beta$. There are four ways contagions can occur, and they are described in Table 1 .

Table 1.

Transmission possibilities.

Susceptible	Infected	Transmission term
$S_n$	$I_n$	${\displaystyle \frac{\beta S_n{I}_n}{N}}$
$S_n$	$I_m$	${\displaystyle \frac{r\beta S_n{I}_m}{N}}$
$S_m$	$I_n$	${\displaystyle \frac{r\beta S_m{I}_n}{N}}$
$S_m$	$I_m$	${\displaystyle \frac{r^2\beta S_m{I}_m}{N}}$

We further assume that $p\left(t\right)=p$ is constant. This is done because our goal is to assess whether the use of masks can, by itself, prevent an epidemic outbreak, so we suppose that a constant amount of the population wears masks in public even in a non-pandemic scenario. This is common in some countries that have dealt with epidemics of respiratory diseases in the past [12]. Thus, $N_m\left(t\right)$ and $N_n\left(t\right)$ are also constant and our model can be written as

$$\begin{array}{cc}{S}_n^{\prime }\hfill & =-{\displaystyle \frac{\beta S_n}{N}}(I_n+r{I}_m)\hfill \\ S_m^{\prime }\hfill & =-{\displaystyle \frac{r\beta S_m}{N}}(I_n+r{I}_m)\hfill \\ E_n^{\prime }\hfill & ={\displaystyle \frac{\beta S_n}{N}}(I_n+r{I}_m)-\sigma E_n\hfill \\ E_m^{\prime }\hfill & ={\displaystyle \frac{r\beta S_m}{N}}(I_n+r{I}_m)-\sigma E_m\hfill \\ I_n^{\prime }\hfill & =\sigma E_n-\gamma I_n\hfill \\ I_m^{\prime }\hfill & =\sigma E_m-\gamma I_m\hfill \\ R_n^{\prime }\hfill & =\gamma I_n\hfill \\ R_m^{\prime }\hfill & =\gamma I_m.\hfill \end{array}$$ (3)

The parameters $\sigma$ and $\gamma$ denote the exit rates from the exposed and infected classes, respectively. It is typically assumed that $\sigma =1/T_e$ and $\gamma =1/T_i,$ where $T_e$ and $T_i$ are the mean lengths of the latency and infectious periods, respectively.

3. The basic reproductive number and some consequences

Now, the basic reproductive number, $R_0,$ of model (3) is calculated. This will be done by a next generation approach (see [13], [14]). $R_0$ is given by the spectral radius of

$$K=F{V}^{-1},$$

where

$$F=\left(\begin{array}{cccc}0& 0& \beta (1-p)& \beta r(1-p)\\ 0& 0& \beta rp& \beta r^{2}p\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$

and

$$V=\left(\begin{array}{cccc}\sigma & 0& 0& 0\\ 0& \sigma & 0& 0\\ -\sigma & 0& \gamma & 0\\ 0& -\sigma & 0& \gamma \end{array}\right).$$

Hence, $K=F{V}^{-1}$ is

$$K=\left(\begin{array}{cccc}\frac{\beta (1-p)}{\gamma }& \frac{r\beta (1-p)}{\gamma }& \frac{\beta (1-p)}{\gamma }& \frac{r\beta (1-p)}{\gamma }\\ \frac{r\beta p}{\gamma }& \frac{r^2\beta p}{\gamma }& \frac{r\beta p}{\gamma }& \frac{r^2\beta p}{\gamma }\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right).$$

Due to its block structure, the eigenvalues of $K$ are exactly the eigenvalues of

$$K_{11}=\left(\begin{array}{cc}\frac{\beta (1-p)}{\gamma }& \frac{r\beta (1-p)}{\gamma }\\ \frac{r\beta p}{\gamma }& \frac{r^2\beta p}{\gamma }\end{array}\right).$$

It is clearly seen that the trace and the determinant of $K_{11}$ are

$$\mathrm{Tr}\left(K_{11}\right)=\frac{\beta }{\gamma }(1-p+r^{2}p),\det \left(K_{11}\right)=0,$$

respectively, hence its eigenvalues are 0 and

$$R_0={\mathcal{R}}_0[1-p(1-r^2)],$$ (4)

where

$${\mathcal{R}}_0=\frac{\beta }{\gamma },$$ (5)

which is the basic reproductive number for the standard SEIR model without vital dynamics (6) [15].

$$\begin{array}{cc}{S}^{\prime }\hfill & =-\beta \frac{SI}{N},\hfill \\ E^{\prime }\hfill & =\beta \frac{SI}{N}-\sigma E,\hfill \\ I^{\prime }\hfill & =\sigma E-\gamma I,\hfill \\ R^{\prime }\hfill & =\gamma I.\hfill \end{array}$$ (6)

Note that (3) reduces to (6) if either $p=0$ (nobody wears masks) or $r=1$ (the masks offer no protection against the disease).

We now look for conditions the pair $(r,p)$ should satisfy so that $R_0<1$. Notice that, for fixed $r\in [0,1],$ $R_0$ is a decreasing function of $p$ (see Fig. 1 ). For $p=0,$ we have $R_0={\mathcal{R}}_0,$ and for $p=1,$ we have $R_0={\mathcal{R}}_1,$ where

$${\mathcal{R}}_1={\mathcal{R}}_0·r^2.$$ (7)

Fig. 1.

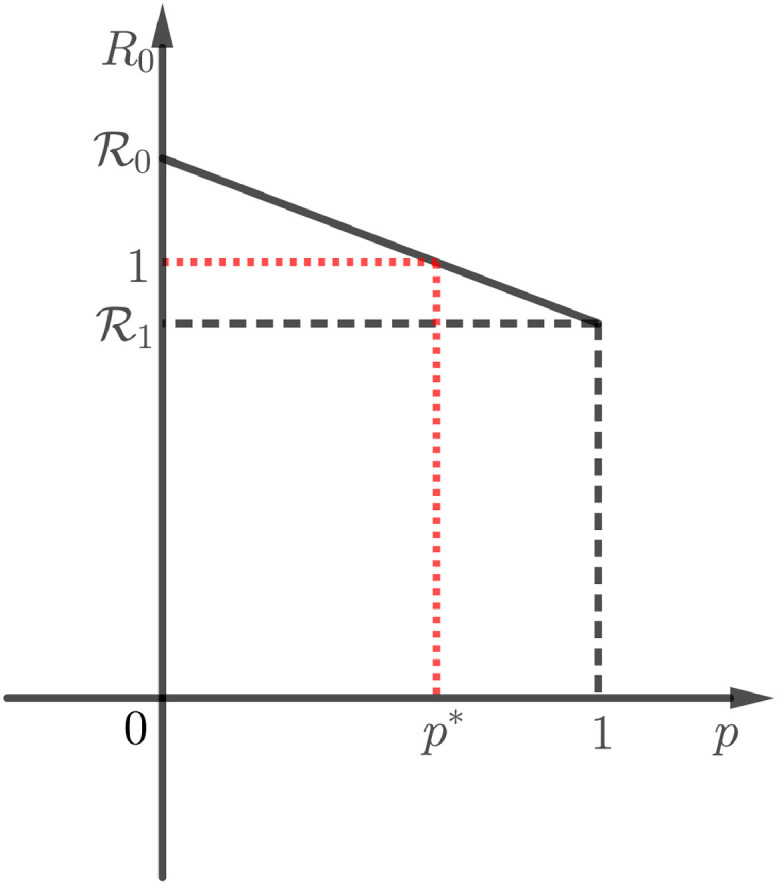
Plot of $R_0$ as a function of $p$.

It is assumed that ${\mathcal{R}}_0>1$. Then, it is clear from Fig. 1 that one can find values of $p$ such that $R_0<1$ if and only if ${\mathcal{R}}_1<1,$ that is, if and only if

$$r<\frac{1}{\sqrt{{\mathcal{R}}_0}}.$$ (8)

Moreover, there is a critical value $p^{*}$ such that $R_0\left(p^{*}\right)=1,$ so $R_0\left(p\right)<1$ if and only if $p>p^{*}$. Solving $R_0=1$ in (4), one sees that

$$p^{*}=\frac{1}{1-r^2}(1-\frac{1}{{\mathcal{R}}_0}).$$ (9)

The value of $p^{*}$ corresponds to the critical percentage of the population that should wear masks in order to avoid the epidemic outbreak. In the extreme case of $r=0,$ i.e., the masks are ideal and avoid contamination for users, which is the same as immunizing the population, (9) becomes

$$p^{*}=1-\frac{1}{{\mathcal{R}}_0},$$ (10)

which coincides with the usual threshold for herd immunity [16].

4. Data fitting and numerical results

In this Section, we collect data from the United States, Brazil and Italy to use as case studies for the results of the previous Section. The time frame in consideration consists of the first 30 days after the cumulative number of cases in each country reached 100, which happened in March 2, March 13 and February 23 for the US, Brazil and Italy, respectively. The data, which was retrieved from [17], is displayed in Table 2, Table 3, Table 4 .

Table 2.

Cumulative cases in the USA starting at the first day with at least 100 cases.

Day	Cases	Day	Cases	Day	Cases	Day	Cases	Day	Cases
1	100	7	541	13	2774	19	19,608	25	86,668
2	124	8	704	14	3622	20	24,498	26	105,584
3	158	9	994	15	4611	21	33,946	27	125,250
4	221	10	1301	16	6366	22	44,325	28	145,526
5	319	11	1631	17	9333	23	55,579	29	168,835
6	435	12	2185	18	13,935	24	69,136	30	194,127

Table 3.

Cumulative cases in Brazil starting at the first day with at least 100 cases.

Day	Cases	Day	Cases	Day	Cases	Day	Cases	Day	Cases
1	151	7	640	13	2554	19	5717	25	12,183
2	151	8	970	14	2985	20	6880	26	14,034
3	200	9	1178	15	3417	21	8044	27	16,188
4	234	10	1546	16	3904	22	9194	28	18,145
5	346	11	1924	17	4256	23	10,360	29	19,789
6	529	12	2247	18	4630	24	11,254	30	20,962

Table 4.

Cumulative cases in Italy starting at the first day with at least 100 cases.

Day	Cases	Day	Cases	Day	Cases	Day	Cases	Day	Cases
1	157	7	1128	13	4639	19	15,122	25	35,732
2	229	8	1702	14	5886	20	17,670	26	41,056
3	323	9	2038	15	7380	21	21,169	27	47,044
4	470	10	2504	16	9179	22	24,762	28	53,598
5	655	11	3092	17	10,156	23	27,997	29	59,158
6	889	12	3861	18	12,469	24	31,524	30	63,941

We assume that the mean latency and recovery periods are 5.1 and 7 days, respectively, as in Eikenberry et al. [7]. We fit $\beta$ by a minimization routine based on the least squares method, available in Martcheva [13], in the standard SEIR model without vital dynamics (6). The routine minimizes the difference of the cumulative number of cases, given by $I\left(t\right)+R\left(t\right),$ and the data points. The MATLAB code is available online in [18].

The total populations of the USA, Brazil and Italy will be rounded to 331, 209 and 60 million, respectively. These numbers will be taken as the initial values of susceptible individuals in each country. In the first days of each data set, the numbers of active cases (see [17]) were 85, 150 and 152 for the USA, Brazil and Italy, respective, so the initial conditions for infected and removed individuals will be taken, respectively, as 85 and 15 for the USA, 150 and 1 for Brazil and 152 and 5 for Italy.

For the initial values of exposed individuals, we use the fact that the latency period is taken as 5.1 days, so we look at the number in day 6 of each data set and choose the initial number of exposed as the extra number of cases since day 1. Hence, these numbers are 335 in the USA, 378 in Brazil and 732 in Italy. A summary of the initial conditions for each country in the minimization routine is shown in Table 5 .

Table 5.

Initial conditions for the estimation of $\beta$.

Country	S(0)	E(0)	I(0)	R(0)
USA	331 million	335	85	15
Brazil	209 million	378	150	1
Italy	60 million	732	152	5

Starting with an initial guess of $\beta =0.5,$ the fitted values of $\beta$ are, then,

$${\beta }_{US}=0.8577,{\beta }_{BR}=0.4854,{\beta }_{IT}=0.5809.$$ (11)

Using (5), we can calculate the value of $R_0$ for each country. The results are displayed in Table 6 .

Table 6.

Basic reproductive number for each country in the standard SEIR model.

Country	${\mathcal{R}}_0$
USA	6.0039
Brazil	3.3978
Italy	4.0663

According to [19], when both individuals wear masks in a susceptible-infected contact, there is an average reduction of $82.18\%$ in the transmission, so

$$r^2=1-0.8218=0.1782,$$

hence $r=0.4221$. Then, the result of one person wearing a mask when two individuals meet is a decrease of around $58\%$ in the transmission coefficient.

Rewriting (8), we see that the outbreak can be avoided by a widespread use of masks is

$${\mathcal{R}}_0<\frac{1}{r^2}\approx 5.6117.$$

According to Table 6, the COVID-19 crisis could have been avoided in Brazil and in Italy, and according to (9), this would be possible if at least $85.87\%$ and $91.76\%$ of all individuals wore masks, respectively.

On the other hand, Table 6 indicates that COVID-19 could not have been avoided in the USA by widespread mask use only, but the basic reproductive number could be lowered from ${\mathcal{R}}_0=6.0039$ to ${\mathcal{R}}_1=1.0699,$ so other a combination with control measures such as social distancing, quarantines and tracking infected cases could be able to prevent the disease outbreak. This could also be done by improving the average mask protection.

Moreover, one could also calculate the normalized forward sensitivity index (or elasticity) of $R_0$ with respect to $p$ (see [13], [20]), given by

$${{\rm Y}}_p^{R_0}=\frac{\partial R_0}{\partial p}·\frac{p}{R_0},$$ (12)

This number provides the percentage change in $R_0$ for a given percentage change in $p$. For example, if ${{\rm Y}}_p^{R_0}=-0.5,$ then a $10\%$ increase in $p$ produces a $5\%$ decrease in $R_0$. By (4) and (12), we have

$${{\rm Y}}_p^{R_0}=-\frac{p(1-r^2)}{1-p(1-r^2)},{{\rm Y}}_{\beta }^{R_0}=1,{{\rm Y}}_{\gamma }^{R_0}=-1,{{\rm Y}}_r^{R_0}=\frac{2p{r}^2}{1-p(1-r^2)}.$$ (13)

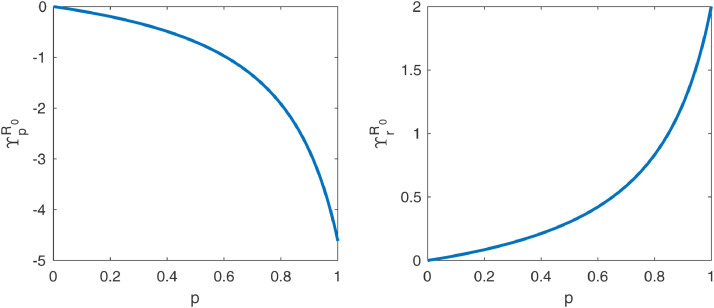
Plots of ${{\rm Y}}_p^{R_0}$ and ${{\rm Y}}_r^{R_0}$ as functions of $p$ are displayed in Fig. 2 . It shows that $R_0$ becomes very sensitive to $p$ for bigger values of this parameter, so even if most of a community has already become adept to wearing masks, small increases in $p$ could still contribute greatly to epidemic control. The plots also show that the absolute values of the sensitivity indexes become greater than 1 (which is the absolute value of the sensitivity of $R_0$ with regard to $\beta$ and $\gamma$) for $p$ sufficiently close to 1, showing that $p$ and $r$ are the parameters to which $R_0$ is most sensitive when a sufficiently large portion of the population adheres to the use of masks in public.

Fig. 2.

Plot of the normalized forward sensitivity index of $R_0$ with respect to $p$ and $r$ as functions of $p$.

We now assess the effect of variations in $p$ on the numbers of infected caused by COVID-19 in the case of the USA. A comparison of the total infected curve

$$I_n\left(t\right)+I_m\left(t\right),$$

normalized by the total population and with initial conditions

$$\begin{array}{cccccccc}{S}_n\left(0\right)\hfill & =(1-p)N,\hfill & S_m\left(0\right)\hfill & =pN,\hfill & E_n\left(0\right)\hfill & =0,\hfill & E_m\left(0\right)\hfill & =0,\hfill \\ I_n\left(0\right)\hfill & =0,\hfill & I_m\left(0\right)\hfill & =1,\hfill & R_n\left(0\right)\hfill & =0,\hfill & R_m\left(0\right)\hfill & =0,\hfill \end{array}$$ (14)

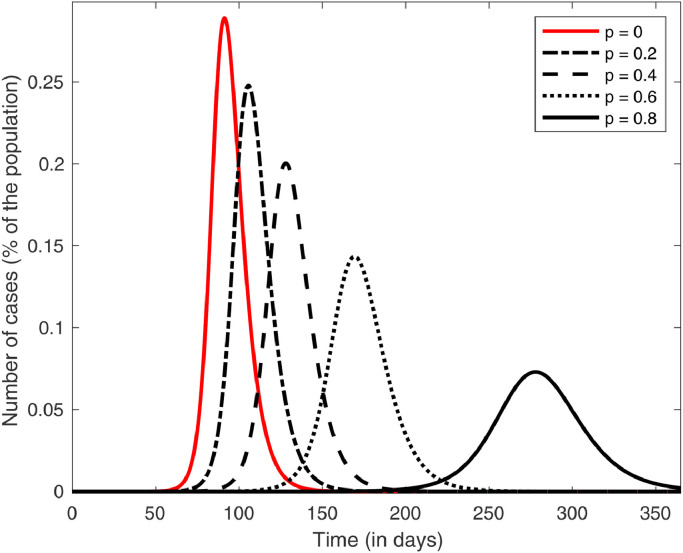
where $N=331$ million, is displayed in Fig. 3 for a time period of one year.

Fig. 3.

Plots of the infected curves for different values of $p$ in model (3) in the case of the USA.

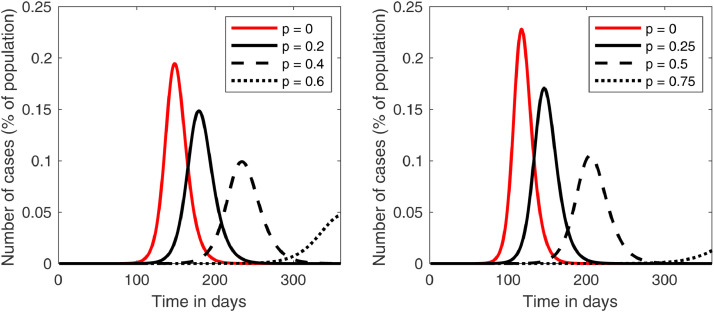
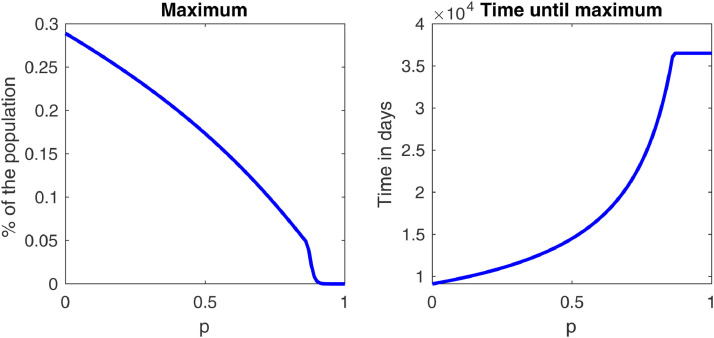
For comparison, the plots of the infected curves for different values of $p$ are added in Fig. 5 in the cases of Brazil and Italy. The desired “flattening of the curve”, i.e., postponing and lowering the maximum number of cases, is achieved. A closer look at this fact is shown in Fig. 4 , which shows that, in a period of one year, both the maximum and the time it happens stabilize after $p\approx 0.86$. For these values of $p,$ plots like the ones in Fig. 3 would only reach their peak after one year, so we can say that the disease is essentially controlled. Fig. 5 shows that this happens for smaller values of $p$ in Brazil and Italy, which is expected, since in these countries we showed that avoiding the outbreak was possible by the methods proposed in this paper.

Fig. 5.

Plots of the infected curves for different values of $p$ in model (3) in the case of Brazil (left) and Italy (right).

Fig. 4.

Plots of the maximum of the infected curve and of the time until the maximum is reached as functions of $p$ in the USA case.

5. Conclusion

In this paper, a SEIR model is considered in a population that is divided into individuals that wear masks and individuals that do not. Parameters $p$ and $r,$ which represent the (constant) percentage of the population that are mask users and the reduction in the transmission rate due to one person wearing a mask in a susceptible-infected contact, respectively, are introduced, and their effect on the basic reproductive number is calculated by a next generation method.

This allows for the derivation of a necessary and sufficient condition for epidemic outbreaks to be prevented only by the widespread use of masks. When this is possible, a critical percentage $p^{*}$ of mask users in the population necessary for disease control is calculated.

This is utterly important in dealing with public health crisis worldwide, since pharmaceutical measures such as vaccines and drugs are more laborious and take long times to be developed while diseases spread. Moreover, if the outbreak can be avoided simply by a widespread adoption of wearing masks in public, then interventions such as quarantines, which cause economic problems, would not be necessary.

As case studies for the results in this paper, real world data from the COVID-19 pandemic was used, focusing on the United States, Brazil and Italy for the first 30 days after the total number of cases reached 100. After fitting the parameters, the results implied that the COVID-19 epidemic could have been avoided in Brazil and Italy if at least 85.87% and 91.76% of the populations, respectively, wore masks from the beginning of the outbreak.

Even though this was not possible in the case of the United States, we noted that the basic reproductive number could have been reduced from 6.0039 to 1.0699, so other control measures such as social distancing, quarantines, or even improving the average mask quality could help pushing this number below 1.

Furthermore, numerical simulations showed that the flattening of the infected curve is achieved as $p$ gets closer to 1, and that the maximum of this curve and the necessary time for it to happen stabilize after $p\approx 0.86,$ i.e., the disease is essentially controlled. Thus, simple measures such as wearing masks can prove to be very effective in controlling, or even preventing, future epidemics.

CRediT authorship contribution statement

João A.M. Gondim: Conceptualization, Methodology, Software, Validation, Resources, Formal analysis, Investigation, Data curation, Writing - original draft, Writing - review & editing, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.