A novel grey model based on traditional Richards model and its application in COVID-19

Highlights

• •A novel grey Richards model GERM(1,1,$e^{at}$) is proposed.
• •The optimal nonlinear terms and background value of the novel model are determined by Genetic algorithm.
• •The comparative study shows that the new model is superior to the other seven benchmark models.
• •The predict the daily number of new confirmed cases of COVID-19 of four regions are projected.

Abstract

In 2020, a new type of coronavirus is in the global pandemic. Now, the number of infected patients is increasing. The trend of the epidemic has attracted global attention. Based on the traditional Richards model and the differential information principle in grey prediction model, this paper uses the modified grey action quantity to propose a new grey prediction model for infectious diseases. This model weakens the dependence of the Richards model on single-peak and saturated S-shaped data, making Richards model more applicable, and uses genetic algorithm to optimize the nonlinear terms and the background value. To illustrate the effectiveness of the model, groups of slowly growing small-sample and large-sample data are selected for simulation experiments. Results of eight evaluation indexes show that the new model is better than the traditional GM(1,1) and grey Richards model. Finally, this model is applied to China, Italy, Britain and Russia. The results show that the new model is better than the other 7 models. Therefore, this model can effectively predict the number of daily new confirmed cases of COVID-19, and provide important prediction information for the formulation of epidemic prevention policies.

1. Introduction

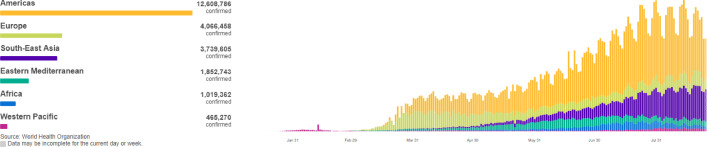
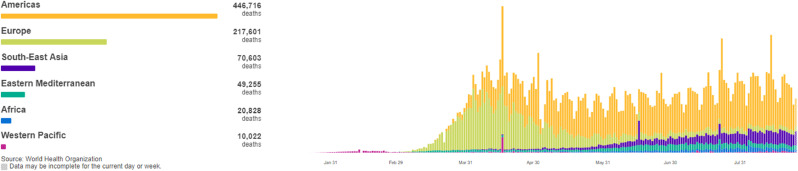
In 2020, a new type of coronavirus (COVID-19) has broken out across the world. The World Health Organization (WHO) has announced that COVID-19 has entered a global pandemic. Till now, data from the WHO [1] shows that more than 20 million confirmed cases of COVID-19 have been reported globally. After breaking the 10 million mark on June 28, the number of confirmed cases worldwide has doubled in about six weeks. In recent months, the change trend of six regions worldwide is shown in Fig. 1 [1]. Fig. 1 shows that the center of the epidemic has moved from the Western Pacific region to Europe at the beginning, and is currently staying in the Americas. The daily number of newly diagnosed patients in the six regions shows a fluctuating S-shaped trend. According to the death toll trend chart in Fig. 2 [1], except for the Americas, the death toll in other regions is basically under control at this stage. During the virus outbreak stage, the death rate in individual countries exceeded 10%, and the death rate in most countries between 5% and 10%, the total death toll at this stage has exceeded 700,000. The global epidemic is still severe, so the worldwide spread of the epidemic is an important research topic. Effectively predicting the daily number of newly confirmed cases of COVID-19 is of great significance to the formulation of epidemic prevention and control policies and the development of economic and social activities during the entire stage of the epidemic, especially to provide important forecast information for the allocation of medical resources and policy formulation during the outbreak.

Fig. 1.

New daily confirmed cases of COVID-19.

Fig. 2.

New daily death cases in world.

Now, there are three main types of prediction methods for COVID-19: 1. Traditional infectious disease model; for example, Jia et al. [2] used a dynamic expansion susceptibility clearance model(eSIR) of infectious diseases with different intervention effects in different periods to estimate the epidemic trend in Italy. Bastos et al. [3] used the SIR model with added parameters to model and predict the evolution of the Brazilian COVID-19 pandemic. Yang et al. [4] used population migration data and the latest COVID-19 epidemiological data to integrate into the SEIR model to obtain the epidemic curve. 2. Machine learning model; for example, Tomara and Guptab [5] used data-driven estimation methods such as long-term memory (LSTM) and curve fitting to predict the number of cases of COVID-19 in India and the impact of preventive measures such as social isolation and blockade on the transmission of COVID-19 in India. Hu et al. [6] developed an improved stacked automatic encoder and predicted the cumulative confirmed case curve in China. Sina et al. [7] compared and analyzed machine learning model and soft computing model to predict the outbreak of COVID-19. 3. Time series model; for example, Petropoulos and Makridakis [8] used the exponential smoothing model to predict the confirmed cases of COVID-19, and the results showed that the number of confirmed COVID-19 cases would continue to increase. Benvenuto et al. [9] used the autoregressive integrated moving average model (ARIMA) to predict the epidemiological trend of COVID-19 prevalence and incidence rate in 2019. Maleki et al. [10] proposed a regression time series model based on two scale mixed normal distribution to analyze the real time series data of confirmed and recovered COVID-19 cases. All the above prediction models can effectively fit and predict the development of COVID-19 epidemic.

However, the epidemic model is hypothetical and may be affected by factors such as geography and super communicators [11]. From the above three types of models, it can be seen that the infectious disease model and time series model may need a large amount of data for accurate parameter identification. Literatures [12], [13], [14] point that the machine learning model may need a large amount of data for training and testing to achieve accurate results. In the research on the development trend of infectious diseases, Richards model [15] has been widely used in a variety of infectious diseases due to its advantages in processing saturated S-shaped data. Hsieh [16] used Richards model to fit the number of SARS cases in many places in China, and estimated the parameters and the maximum number of cases to illustrate the turning point. Hsieh and Ma [17] matched the Richards model with dengue fever notification numbers to detect turning points in the epidemic. Chan et al. [18] used Richards model to estimate the basic reproductive number (R0) of cholera and the proportion of unrecognized cases. The heterogeneity of R0 estimates generated by the model was consistent with the dynamic changes of cholera described. Wang et al. [19] started from a simple epidemic SIR model and re-examined the Richards model through the internal connection between the two models. More accurate and stable model parameters and key epidemic characteristics were estimated in H1N1, SARS and other epidemics. The accurate parameter identification of this model is also inseparable from a large-number data.

For the new type of coronavirus such as COVID-19, due to the low availability of case data and incomplete knowledge, especially in the early stage of the outbreak, the information is incomplete and the amount of data is small. The above models may not have obvious effect on the data of uncertainty phenomenon. Therefore, it is considered to be attractive to find a prediction model with less information to obtain relatively effective results [20]. In recent years, in systems that deal with incomplete information, the grey model stands out by virtue of its "simple model, strong adaptability, and easy parameter changes". It is widely used in energy, finance, transportation, environment, manufacturing, materials and other industries [[12], [13], [14],[20], [21], [22], [23], [24], [25]]. In the field of infectious diseases, the grey model is also widely used. Guo et al. [26] used traditional GM(1,1) and SMGM(1,1) based on self-memory principle to predict the incidence of three typical infectious diseases in China. Wang et al. [27] used GM(1,1) for prediction of hepatitis B in China. Zhang et al. [28] used GM(1,1), the grey period extended combined model, and the improved Fourier series grey model to predict Hydatid disease, and these models successfully predicted the development of these diseases. The above models are all based on the GM(1,1) model. The GM(1,1) model is suitable for strong exponential growth data and is a linear model. The research object of this article is the fluctuating S-shaped data, so the applicability of GM(1,1) is limited. Therefore, this paper chooses the nonlinear grey model as a research method to predict the daily number of newly confirmed cases of COVID-19 and provide an important basis for formulating epidemic prevention policies.

In the grey system, the Verhulst model has strong prediction ability for single-peak or saturated S-shaped sequence [29]. Wang et al. [11] used the rolling Verhulst model to predict the final number of COVID-19 infection cases, and good results were achieved. Şahin and Şahin [30] used fractional Nonlinear Grey Bernoulli model to predict the cumulative number of cases in Italy, the United Kingdom and the United States. The Verhulst model is a special form of the grey Bernoulli model, and the whitening equation of the Verhulst model is the logistic model. The Richards model is also a generalized logistic model [15]. Because of its good performance on S-shaped data and its relationship with the Verhulst model, this paper study the corresponding grey prediction model based on the Richards model.

Therefore, based on the characteristics of COVID-19 and the research status of Richards model and grey prediction model, this paper uses the difference information principles of the grey prediction model to derive the grey Richards prediction model on the basis of the Richards model, and the grey covid-19 prediction model (GERM(1,1,$e^{at}$)) is established with the help of the effect of grey action quantity. Using the relevant grey knowledge to solve the model, the time response function of the model is obtained, and the properties of the optimization model are studied. Through practical cases, the results of the new model are compared with the grey linear model, the grey nonlinear model and the autoregressive model, so as to verify the effectiveness of the model and provide important information for the government to formulate economic policies.

So, the main contributions of this paper are as follows:

• 1Richards model is widely used in many kinds of infectious diseases. Based on the structure of traditional Richards growth model and the differential information principle, namely the relationship between differential equation and difference equation, the traditional Richards growth model is transformed into corresponding grey prediction model.
• 2Due to the limitation of the traditional model for data trend, the new model uses natural index to improve the grey action of the grey Richards model, and optimizes the nonlinear term and background value of the model by GA algorithm, so as to weaken or even eliminate the dependence of the traditional Richards model on saturated S-shaped data, and improve the accuracy and applicability of the traditional model, which is also a generalization of Richards model and grey prediction model.
• 3Through the empirical analysis of small-sample and large-sample data, it shows that the new model can effectively carry out short-term and medium-term prediction and makes up for the defects of grey prediction model generally used for short-term prediction. The new model also effectively predicts the daily number of newly confirmed COVID-19 cases in four countries, which will provide help for local governments to make policy decisions.

The rest of this paper is as follows: Section 2 establishes the GERM(1,1,$e^{at}$) model, and studies the properties and mechanism of the new model; Section 3 analyses the validity of the new model; Section 4 discusses the application of the GERM(1,1,$e^{at}$) model. Section 5 presents the conclusions.

In the full text, the different abbreviations are for different grey prediction models. Abbreviations and their meanings are listed in Table 1 .

Table 1.

Abbreviations of models.

Number	Abbreviation	Definition
1.	GM(1, 1)	Grey model with one variable and one first order equation [31]
2.	Verhulst	Verhulst grey model [32]
3.	ARGM(1,1)	Autoregressive grey model [33]
4.	ONGM(1,1)	Optimized NGM(1,1,k,c) model [34]
5.	ENGM(1,1)	Exact nonhomogeneous grey model [35]
6.	ARIMA	Autoregressive Integrated Moving Average model [36]
7.	NGBM(1,1)	Nonlinear Grey Bernoulli Model [37]
8.	GRM(1,1)	Grey Richards model
9.	GERM(1,1,$e^{at}$)	Grey Extend Richards model

2. Theoretical modeling of GERM(1,1,$e^{at}$)

This section first introduces the related concepts and properties of Richards model, then establishes the corresponding grey prediction model according to the grey difference information and grey action quantity, and finally optimizes the parameters of the new model by GA algorithm.

2.1. Classical growth Richards model

The logistic model was first proposed by Verhulst [38] in 1838 to simulate population growth after Malthus model [39]. The model equation, also known as Verhulst equation, is as follows:

$$C^{\prime }\left(t\right)=rC\left(t\right)\left(1-\frac{C\left(t\right)}{K}\right).$$ (1)

Where $C\left(t\right)$ is the population size in question at time $t$, $r$ is the intrinsic growth rate, and $K$ is maximum capacity.

In 1959, Richards [15] proposed the following modification of the logistic model to model growth of biological populations:

$$C^{\prime }\left(t\right)=rC\left(t\right)\left(1-{\left(\frac{C\left(t\right)}{K}\right)}^{\alpha }\right),$$ (2)

where, $C\left(t\right)$ is the cumulative number of infection cases at time $t$, $K$ is the carrying capacity of the outbreak or the total number of cases, $r$ is the per capita growth rate of the infected population, parameter $\alpha$ provides the flexibility measure of S-shaped curvature shown by the result solution curve, that is, the degree of deviation from the S-shape dynamics of the classical logistic growth model. When $\alpha =1$, Richards model becomes the logistic model. Richards model is used to predict the spread of diseases. It only considers the cumulative population size with saturated growth as the model and dynamics of infectious disease outbreak and development, which is due to the reduction of cases due to the attempt to avoid contact and the implementation of control measures.

2.2. Description of the GRM(1,1)model

Let the daily number of newly confirmed cases be

$$X^{\left(0\right)}=(x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\cdots ,x^{\left(0\right)}\left(n\right)),$$ (3)

The first- accumulating generation operator(1-AGO) sequence is

$$X^{\left(1\right)}=(x^{\left(1\right)}\left(1\right),x^{\left(1\right)}\left(2\right),\cdots ,x^{\left(1\right)}\left(n\right)),$$ (4)

where $x^{\left(1\right)}\left(k\right)=\sum _{i=1}^k{x}^{\left(0\right)}\left(i\right),k=1,2,\cdots n.$

Eq. (2) is a first-order nonlinear differential equation, which is continuously differentiable and contains infinite information. However, the number of confirmed cases per unit time is only a discrete time series with limited uncertain information or so-called grey information. Therefore, Eq. (2) should be transformed and discretized according to the principle of differential information, so as to adapt to the characteristics of grey information [40]. This principle is also an important cornerstone of grey model [31]. It is systematically and accurately described in monograph [41].

Therefore, the grey Richards model (GRM(1,1)) is introduced as below. In Eq. (2), $C\left(t\right)$ represents the number of all the patients diagnosed in unit time, that is, the total number of all patients diagnosed in a certain period of time. According to different unit time, it can be the number of patients diagnosed per minute, the number of patients diagnosed per hour, the number of patients diagnosed daily, and the number of patients diagnosed per week. If the initial time point is recorded as $t_0=1$, then the number of confirmed patients is recorded $k$ times between the time periods $[t_0,t]$, and the number of all patients diagnosed is

$$C\left(t\right)=C\left(k\right)=\sum _{i=1}^k{c}^{\left(0\right)}\left(i\right),$$ (5)

$C\left(t\right)$ is a 1-AGO sequence $X^{\left(1\right)}\left(t\right)$ of Eq. (4), which is similar to that of oil production in a certain period of time in [42,43] and energy consumption in a certain period in [44]. Therefore, according to Eq. (2), the following formula holds

$$\frac{d{X}^{\left(1\right)}\left(t\right)}{dt}=r{X}^{\left(1\right)}\left(t\right)-\frac{r}{K^a}{\left(X^{\left(1\right)}\left(t\right)\right)}^{1+a}.$$ (6)

Substituting the first-order difference for the differential at the left end of Eq. (6), then at $t=k$:

$$\begin{array}{c}\frac{d{X}^{\left(1\right)}\left(t\right)}{dt}{|}_{t=k}\approx \frac{\Delta X^{\left(1\right)}\left(t\right)}{\Delta t}{|}_{t=k}=\frac{X^{\left(1\right)}\left(k\right)-X^{\left(1\right)}(k-1)}{k-(k-1)}=X^{\left(1\right)}\left(k\right)-\hfill \\ X^{\left(1\right)}(k-1)=X^{\left(0\right)}\left(k\right).\hfill \end{array}$$ (7)

Thus, the following grey prediction models can be defined:

Definition 1

Set $X^{\left(0\right)}$ and $X^{\left(1\right)}$ as Eqs. (3) and (4), then the sequence $Z^{\left(1\right)}$ is called the nearest mean generating sequence of $X^{\left(1\right)}$:

$$Z^{\left(1\right)}=\{z^{\left(1\right)}\left(1\right),z^{\left(1\right)}\left(2\right),\cdots ,z^{\left(1\right)}\left(n\right)\},$$ (8)

where $z^{\left(1\right)}\left(k\right)=(X^{\left(1\right)}\left(k\right)+X^{\left(1\right)}(k-1))/2$.

It should be noted that $X^{\left(0\right)}\left(k\right)$ is usually regarded as a grey derivative and can provide the necessary information related to the time-dependent function $X^{\left(1\right)}\left(t\right)$. That is, $X^{\left(0\right)}\left(k\right)$ can be regarded as the grey derivative sequence of $X^{\left(1\right)}\left(t\right)$ and replace $\frac{d{X}^{\left(1\right)}\left(t\right)}{dt}$ during $[k-1,k]$. In addition, the background value $Z^{\left(1\right)}\left(t\right)$ of $X^{\left(0\right)}\left(k\right)$ can be formalized as

$$X^{\left(1\right)}\left(t\right)|{}_{\left[k-1,k\right]}\approx \frac{1}{2}(X^{\left(1\right)}\left(k\right)-X^{\left(1\right)}(k-1))=Z^{\left(1\right)}\left(k\right).$$ (9)

Definition 2

Set $X^{\left(0\right)}$, $X^{\left(1\right)}$ and $Z^{\left(1\right)}$ as Eqs. (3), (4) and (8), so,

$$X^{\left(0\right)}\left(t\right)-r{Z}^{\left(1\right)}\left(t\right)=-\frac{r}{K^a}{\left(Z^{\left(1\right)}\left(t\right)\right)}^{1+a},$$ (10)

is grey Richards model (GRM(1,1)). Set $a=-r,b=-\frac{r}{K^a},\gamma =1+a$, Eq. (10) becomes

$$X^{\left(0\right)}\left(t\right)+a{Z}^{\left(1\right)}\left(t\right)=b{\left(Z^{\left(1\right)}\left(t\right)\right)}^{\gamma },$$ (11)

Eq. (11) is also a power model in grey model.

Since the daily data of new patients of COVID-19 shows a fluctuating S-shaped trend, and Richard model is suitable for processing data close to single-peak and saturated S-shaped [15], [16], [17], [18], [19], this paper uses a new grey action to improve structure of the grey Richard model, it is suitable for the prediction of daily number of confirmed cases of COVID-19.

2.3. Description of the GERM(1,1,$e^{at}$) model

Obviously, the optimization of grey action is an effective mean to improve the performance and applicability of grey model [45]. In this section, a new driving grey model is proposed, which takes the natural exponential function of time as the grey action quantity. Therefore, this section gives the definition of the grey extended Richards model, the time response function and the restored values of the model.

Definition 3

Based on the Sections 2.1 and 2.2, the Grey Extend Richards model (GERM(1,1,$e^{at}$)) is defined as

$$\frac{d{x}^{\left(1\right)}\left(t\right)}{dt}+a{x}^{\left(1\right)}\left(t\right)=(b{e}^{\alpha t}+c){\left(x^{\left(1\right)}\left(t\right)\right)}^{\gamma }.$$ (12)

where $a$ is the development coefficient, the term $b{e}^{\alpha t}+c$ denotes the power-driven grey input. $\alpha$ and $\gamma$ are nonlinear quantities which can be tunable.

If $\gamma =0$, the GERM(1,1,$e^{at}$) becomes GM(1,1,$e^{at}$) [45]. Set $y^{\left(1\right)}\left(t\right)={\left(x^{\left(1\right)}\left(t\right)\right)}^{1-\gamma }$, Eq. (12) becomes

$$\frac{d{y}^{\left(1\right)}\left(t\right)}{dt}+(1-\gamma )a{y}^{\left(1\right)}\left(t\right)=(1-\gamma )(b{e}^{\alpha t}+c).$$ (13)

The solution of Eq. (13) is

$$\begin{array}{c}{y}^{\left(1\right)}\left(t\right)=\left(y^{\left(0\right)}\left(1\right)-\frac{b(1-\gamma )}{(1-\gamma )a+\alpha }-\frac{c}{a}\right)e^{-(1-\gamma )a(t-1)}+\hfill \\ \frac{b(1-\gamma )}{(1-\gamma )a+\alpha }{e}^{\alpha t}+\frac{c}{a}.\hfill \end{array}$$ (14)

So, based on the $x^{\left(1\right)}\left(t\right)={\left(y^{\left(1\right)}\left(t\right)\right)}^{\frac{1}{1-\gamma }}$, the time response function can be derived from Eq. (14) by

$$\begin{array}{c}{\widehat{x}}^{\left(1\right)}\left(k\right)=\{\left[{\left(x^{\left(0\right)}\left(1\right)\right)}^{1-\gamma }-\frac{b(1-\gamma )}{(1-\gamma )a+\alpha }-\frac{c}{a}\right]e^{-(1-\gamma )a(t-1)}+\hfill \\ {\frac{b(1-\gamma )}{(1-\gamma )a+\alpha }{e}^{\alpha t}+\frac{c}{a}\}}^{\frac{1}{1-\gamma }},\hfill \end{array}$$ (15)

where $k=2,3,\cdots ,n$, and the restored value is

$${\widehat{x}}^{\left(0\right)}\left(k\right)={\widehat{x}}^{\left(1\right)}\left(k\right)-{\widehat{x}}^{\left(1\right)}(k-1).$$ (16)

Definition 4

Assume $X^{\left(0\right)}$ and $X^{\left(1\right)}$ are defined as the same in Definition 1. The background value is optimized by extrapolation background value [23], $Z_y\left(k\right)$ is defined as

$$Z_y\left(k\right)=(1+\beta )y^{\left(1\right)}\left(k\right)-\beta y^{\left(1\right)}(k-1),\beta \in (-1,+\infty ).$$ (17)

So, the parameters of GERM(1,1,$e^{at}$) are computed by the following expression

$$P={\left(a,b,c\right)}^T={\left(B^{T}B\right)}^{-1}{B}^{T}X,$$ (18)

where $B=(1-\gamma )\left(\begin{array}{ccc}{z}_y\left(2\right)& -\frac{e^{\alpha }+e^{2\alpha }}{2}& -1\\ z_y\left(3\right)& -\frac{e^{3\alpha }+e^{2\alpha }}{2}& -1\\ ⋮& ⋮& ⋮\\ z_y\left(n\right)& -\frac{e^n+e^{(n-1)\alpha }}{2}& -1\end{array}\right),Y=\left(\begin{array}{c}{y}^{\left(1\right)}\left(1\right)-y^{\left(1\right)}\left(2\right)\\ y^{\left(1\right)}\left(2\right)-y^{\left(1\right)}\left(3\right)\\ ⋮\\ y^{\left(1\right)}(n-1)-y^{\left(1\right)}\left(n\right)\end{array}\right).$

Proof

By integrating on both side of Eq. (12), it becomes

$$\begin{array}{c}{\int }_{k-1}^k\frac{d{y}^{\left(1\right)}\left(t\right)}{dt}dt+{\int }_{k-1}^k(1-\gamma )a{y}^{\left(1\right)}\left(t\right)dt={\int }_{k-1}^{k}b{e}^{\alpha t}(1-\gamma )dt+\hfill \\ {\int }_{k-1}^{k}cdt.\hfill \end{array}$$ (19)

It follows from Eq. (19) that

$$\begin{array}{c}{y}^{\left(1\right)}\left(k\right)-y^{\left(1\right)}(k-1)+(1-\gamma )a·{\int }_{k-1}^k{y}^{\left(1\right)}\left(t\right)dt=b(1-\gamma )\times \hfill \\ {\int }_{k-1}^k{e}^{\alpha t}dt+c(1-\gamma ).\hfill \end{array}$$ (20)

Using the trapezoidal formula, the terms ${\int }_{k-1}^k{y}^{\left(1\right)}\left(t\right)dt$ and ${\int }_{k-1}^k{e}^{\alpha t}dt$ can be computed by

$${\int }_{k-1}^k{y}^{\left(1\right)}\left(t\right)dt=\frac{1}{2}{y}^{\left(1\right)}\left(k\right)+\frac{1}{2}{y}^{\left(1\right)}(k-1)\genfrac{}{}{0pt}{}{\Delta }{=}{z^{\left(1\right)}}_y\left(k\right),k=2,3,\cdots ,n,$$ (21)

$${\int }_{k-1}^k{e}^{\alpha t}dt=\frac{1}{2}{e}^{\alpha t}+\frac{1}{2}{e}^{\alpha (t-1)}.$$ (22)

By substituting Eqs. (21) and (22) into Eq. (20), Eq. (20) becomes

$$\begin{array}{c}{y}^{\left(1\right)}\left(k\right)-y^{\left(1\right)}(k-1)+(1-\gamma )a·Z_y\left(k\right)=\frac{1}{2}(e^{\alpha k}+e^{\alpha (k-1)})·\hfill \\ b(1-\gamma )+c(1-\gamma ).\hfill \end{array}$$ (23)

Once $\beta ,\gamma ,\alpha$ are given, the linear parameters can be straightforwardly computed by the following expression

$$P={\left(a,b,c\right)}^T={\left(B^{T}B\right)}^{-1}{B}^{T}X,$$

where

$$\begin{array}{c}B=(1-\gamma )\left(\begin{array}{ccc}{z}_y\left(2\right)& -\frac{e^{\alpha }+e^{2\alpha }}{2}& -1\\ z_y\left(3\right)& -\frac{e^{3\alpha }+e^{2\alpha }}{2}& -1\\ ⋮& ⋮& ⋮\\ z_y\left(n\right)& -\frac{e^n+e^{(n-1)\alpha }}{2}& -1\end{array}\right),\hfill \\ Y=\left(\begin{array}{c}{y}^{\left(1\right)}\left(1\right)-y^{\left(1\right)}\left(2\right)\\ y^{\left(1\right)}\left(2\right)-y^{\left(1\right)}\left(3\right)\\ ⋮\\ y^{\left(1\right)}(n-1)-y^{\left(1\right)}\left(n\right)\end{array}\right).\hfill \end{array}$$

Therefore Definition 4 is proven.

2.4. Error evaluation criteria

This subsection provides some standard error evaluation criteria to measure the accuracy of grey forecasting models. In general, they are defined in Table 2 . Meanwhile, Lewis’ criterion [46] shown in Table 3 is used to illustrate the prediction ability of the model.

Table 2.

Metrics for evaluating effectiveness of the models.

Name	Abbreviation	Formulation
The absolute percentage error	APE	$\left(\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}\right)\times 100\%$
The mean absolute simulation percentage error	MAPESIM	$\frac{1}{n-1}\left(\sum _{i=1}^n|\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}|\right)\times 100\%$
The mean absolute prediction percentage error	MAPEPRE	$\frac{1}{v}\left(\sum _{i=1}^n|\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}|\right)\times 100\%$
The total mean absolute percentage error	MAPETOT	$\frac{1}{n-1}\left(\sum _{i=1}^n|\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}|\right)\times 100\%$
Root mean squares percentage error	RMSPE	$\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(\frac{X^{\left(0\right)}\left(k\right)-{\widehat{X}}^{\left(0\right)}\left(k\right)}{X^{\left(0\right)}\left(k\right)}\right)}^2}\times 100\%$
Mean absolute percentage error	MAE	$\frac{1}{n}\sum _{i=1}^n|X^{\left(0\right)}\left(k\right)-{\widehat{X}}^{\left(0\right)}\left(k\right)|$
Index of agreement	IA	$1-\frac{\sum _{k=1}^n{(X^{\left(0\right)}\left(k\right)-{\widehat{X}}^{\left(0\right)}\left(k\right))}^{{}^2}}{\sum _{k=1}^n{\left(|{\widehat{x}}^{\left(0\right)}\left(k\right)-\overline{x}|+|x^{\left(0\right)}\left(k\right)-\overline{x}|\right)}^{{}^2}}$
Theil U statistic 1	U1	$\frac{\sqrt{\frac{1}{n}\sum _{i=1}^n{(X^{\left(0\right)}\left(k\right)-{\widehat{X}}^{\left(0\right)}\left(k\right))}^2}}{\sqrt{\frac{1}{n}\sum _{i=1}^n{\left[X^{\left(0\right)}\left(k\right)\right]}^2}+\sqrt{\frac{1}{n}\sum _{i=1}^n{\left[{\widehat{X}}^{\left(0\right)}\left(k\right)\right]}^2}}$
Theil U statistic 2	U2	$\frac{{\left[\sum _{i=1}^n{(X^{\left(0\right)}\left(k\right)-{\widehat{X}}^{\left(0\right)}\left(k\right))}^2\right]}^{1/2}}{{\left[\sum _{i=1}^n{\left[X^{\left(0\right)}\left(k\right)\right]}^2\right]}^{1/2}}$
Correlation coefficient	R	$\frac{Cov({\widehat{X}}^{\left(0\right)},X^{\left(0\right)})}{\sqrt{Var\left({\widehat{X}}^{\left(0\right)}\right)Var\left(X^{\left(0\right)}\right)}}$

Table 3.

Lewis’ criterion for model evaluation.

MAPE (%)	Prediction performance
<10	Excellent
10-20	Good
20-50	Reasonable
>50	Incorrect

2.5. Optimization of nonlinear parameters

It can be seen from Section 2.4 that the parameters of GERM(1,1,$e^{at}$) can be obtained through the values of three parameters $\beta ,\gamma ,\alpha$, where $\gamma ,\alpha$ are nonlinear quantities. In this section, the genetic algorithm (GA) is used to search for $\beta ,\gamma ,\alpha$, and MAPE_TOT is taken as the objective function. Then, the mathematical expression of the optimization problem is

$$\begin{array}{c}f:\min MAPE\frac{1}{n-1}\sum _{k=2}^n\left|\frac{x^{\left(0\right)}\left(k\right)-{\widehat{x}}^{\left(0\right)}\left(k\right)}{x^{\left(0\right)}\left(k\right)}\right|\times 100\%\hfill \\ s.t.\{\begin{array}{c}\beta \in \left[-1,\infty \right]\hfill \\ P={(a,b,c)}^T={\left(B^{T}B\right)}^{-1}{B}^{T}Y\hfill \\ \begin{array}{c}{\widehat{x}}^{\left(1\right)}\left(k\right)=\{\left[{\left(x^{\left(0\right)}\left(1\right)\right)}^{1-\gamma }-\frac{b(1-\gamma )}{(1-\gamma )a+\alpha }-\frac{c}{a}\right]e^{-(1-\gamma )a(t-1)}+\hfill \\ {\frac{b(1-\gamma )}{(1-\gamma )a+\alpha }{e}^{\alpha t}+\frac{c}{a}\}}^{\frac{1}{1-\gamma }}\hfill \end{array}\hfill \\ {\widehat{x}}^{\left(0\right)}\left(k\right)={\widehat{x}}^{\left(1\right)}\left(k\right)-{\widehat{x}}^{\left(1\right)}(k-1),k=2,\cdots ,n\hfill \end{array}.\hfill \end{array}$$ (24)

GA is proposed by American Professor John Holland [47]. It randomly searches the optimal value by simulating the genetic law and evolutionary theory of natural organisms. It applies the evolutionary principle of survival of the fittest and elimination of the unfit in the biological world to optimize the parameter individuals after coding. Through selection, variation and crossover, the overall fitness level of the population is improved continuously, which not only inherits the good information of the previous generation, but also is superior to the previous generation. This is repeated until the desired conditions are met. The GA algorithm is utilized to search for optimal $\beta ,\gamma ,\alpha$, and its main procedures are given in Algorithm 1 .

Algorithm 1.

The GA algorithm to find the optimal $\gamma ,\beta ,\alpha$.

Set the objective function and the maximum iteration number Input: The original parameters $\beta ,\gamma ,\alpha$, original data and the number of modelling data Output: The best $\beta ,\gamma ,\alpha$ for $\beta \in \left(-1,+\infty \right)$do Substitute $\beta ,\gamma ,\alpha$ to $\widehat{P}={\left(B^{T}B\right)}^{-1}{B}^{T}Y$ and obtain parameters $P={\left(a,b,c\right)}^T$ Substitute parameters to discrete equation Eq. (14) and compute the simulation value to obtain ${\widehat{X}}^{\left(1\right)}\left(k\right)$ Compute ${\widehat{X}}^{\left(0\right)}\left(k\right)$ in Eq. (16) Compute APE and MAPE in Table 2. End Update the minimum MAPE value Return the best $\beta ,\gamma ,\alpha$ by the GA algorithm.

3. Validation of the GERM(1,1,$e^{at}$) model

This section mainly discusses the effectiveness of the new model through two data sets. The two selected data sets are divided into slowly growing small-sample data and large-sample data to illustrate that the new model has improved the accuracy of GRM(1,1) after modifying the grey action quantity, and the dependence of GRM(1,1) on saturated S-shaped data is weakened. Therefore, the traditional GM(1,1) and GRM(1,1) are selected for comparison. GRM(1,1) is also the form of NGBM(1,1). The validity comparison of the models can be explained from two aspects: 1. Using eight evaluation indexes in Table 2, the smaller APE, MAPE, RMSPE, MAE, MSE, U1 and U2, the higher the accuracy of the model, and vice versa. The higher the values of IA and R, the higher the accuracy of the model. 2. Use the comparison chart of APE value every year.

3.1. Validation case 1: fitting of small-sample data

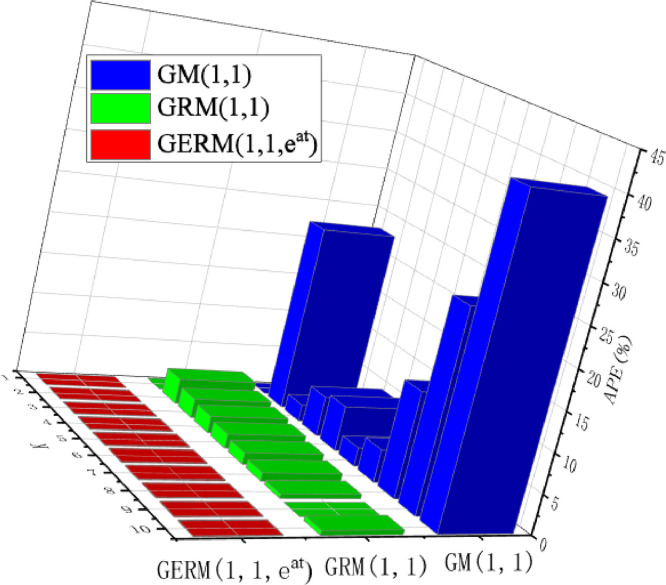
The first case study object is small sample data. The first seven data are used for modeling, and the last three data are used to test the model accuracy. According to GA algorithm, the optimal parameter of GRM(1,1) is $\gamma =0.9818$, the optimal parameters of GERM(1,1,$e^{at}$) are $\gamma ,\beta ,\alpha =[6.6354\times {10}^{-4},-0.9954,-3.1248\times {10}^{-4}]$. The calculation results of three grey models are shown in Table 4 and the index results are shown in Table 5 . In Table 4, the MAPE_SIM and MAPE_PRE of GM(1,1) are the highest. In the modeling phase, MAPE_SIM of GERM(1,1,$e^{at}$) is nearly 2% higher than that of GRM(1,1), and the prediction error is the smallest. In Table 5, the MAPE_TOT of GERM(1,1,$e^{at}$) is 1.3% higher than that of GRM(1,1). In addition, the other indicators of GERM(1,1,$e^{at}$) are good, and the R index reaches 1. In order to further show the fitting effect of the model, the APE value comparison chart is made, as shown in Fig. 3 . In Fig. 3, the APE values of GERM(1,1,$e^{at}$) are basically the lowest, and compared with the other two models, the APE values are almost zero every year. The comparison results of the above two aspects show that the GERM(1,1,$e^{at}$) improves the accuracy of the original GRM(1,1).

Table 4.

Results of three grey models in validation Case 1.

Raw data	GM(1,1) model	APE (%)	GRM (1,1)	APE (%)	GERM (1,1,$e^{at}$)	APE (%)
1	1.0000	0.0000	1.0000	0.0000	1.0000	0.0000
2	2.4658	23.2912	1.9385	-3.0731	1.9994	-0.0312
3	3.0619	2.0644	2.9302	-2.3283	3.0019	0.0633
4	3.8021	-4.9464	3.9194	-2.0157	4.0041	0.1025
5	4.7213	-5.5739	4.9133	-1.7336	5.0061	0.1201
6	5.8627	-2.2889	5.9161	-1.3993	6.0075	0.125
7	7.2802	3.9993	6.9302	-0.9970	7.0088	0.1257
MAPESIM(%)		7.0273		1.9245		0.0944
8	9.0399	12.9983	7.9578	-0.528	8.0097	0.1213
9	11.2252	24.7247	9.0002	0.0021	9.0103	0.1144
10	13.9389	39.3890	10.0587	0.5874	10.0106	0.1061
MAPEPRE(%)		25.704		0.3725		0.1139

Table 5.

Metrics of models in Validation Case 1.

Metrics	GM (1,1)	GRM (1,1)	GERM (1,1,$e^{at}$)	GERM (1,1,$e^{at}$) rank
MAPETOT(%)	19.8793	1.4072	0.1009	1
RMSPE	17.1908	1.5973	0.1001	1
MAE	0.8626	0.0554	0.0060	1
MSE	2.1983	0.0040	5.03E-05	1
IA	0.95181	0.99988	0.999998	1
U1	0.1093	0.0051	0.0005	1
U2	0.2390	0.0102	0.001143	1
R	0.9749	0.9999	1.0000	1

Fig. 3.

APE of the three models in Validation Case 1.

3.2. Validation case 1: fitting of large-sample data

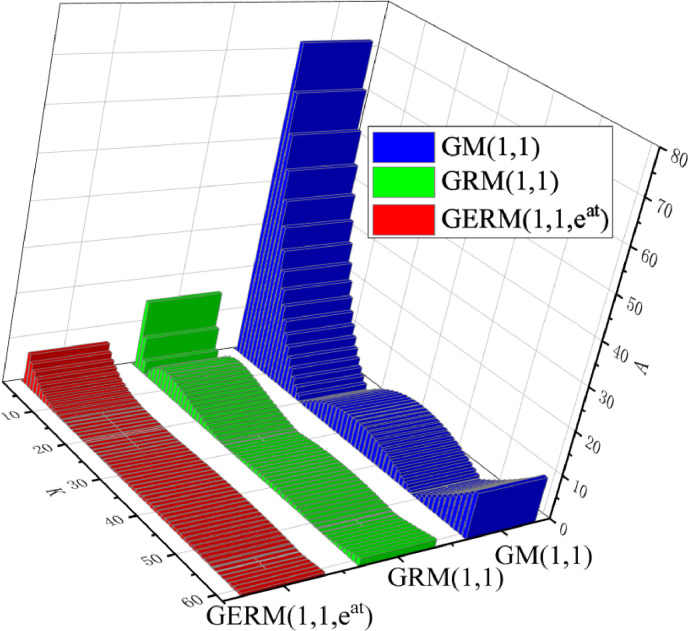
The first case study object is small sample data. The first seven data are used for modeling, and the last three data are used to test the model accuracy. The optimal parameter of GRM(1,1) is $\gamma =0.3108$, the optimal parameters of GERM(1,1,$e^{at}$) found by GA algorithm are $\gamma ,\beta ,\alpha =[3.8128\times {10}^{-5},-0.9999,-0.0239]$. Due to the large amount of data, the original data and the calculation results of the three grey models are shown in Table 12 in Appendix A, and the index results are shown in Table 6 . In Table 6, the MAPE_TOT of GERM(1,1,$e^{at}$) is the lowest, which is 1 percentage point higher than the original GRM(1,1), and the results of other seven indicators are the best. Meanwhile, the R of this cases is also 1. As in the previous case, the APE comparison chart between the models are drawn, as shown in Fig. 4 . In Fig. 4, the APE values of the GERM(1,1,$e^{at}$) are basically the lowest, which is closer to 0 from the 11th point compared with the other two models. In conclusion, GERM(1,1,$e^{at}$) improves the accuracy of GRM(1,1) model.

Table 6.

Metrics of models in Validation Case 1.

Metrics	GM (1,1)	GRM (1,1)	GERM (1,1,$e^{at}$)	GERM (1,1,$e^{at}$) rank
MAPETOT(%)	10.2098	1.7895	0.7782	1
RMSPE	17.1908	1.5973	0.1001	1
MAE	0.8626	0.0554	0.0060	1
MSE	2.1983	0.0040	5.03E-05	1
IA	0.9518	0.99988	0.999998	1
U1	0.1093	0.0051	0.0005	1
U2	0.2390	0.0102	0.001143	1
R	0.9749	0.9999	1.0000	1

Fig. 4.

APE of the three models in Validation Case 2.

3.3. Analysis of result

In two practical cases, MATLAB software is used to calculate the whole simulation process. According to the fitting results of three grey models and APE comparison chart, the following conclusions can be obtained:

• (1)In the contrast test with the eight metrics of traditional GM(1,1) and GRM(1,1) (NGBM(1,1)), those of GERM(1,1,$e^{at}$) are the best. Meanwhile, the APE value of GERM(1,1,$e^{at}$) are basically the lowest, that is to say, its error is the smallest and the accuracy is the highest, indicating that the GERM(1,1,$e^{at}$) is competitive.
• (2)From original GRM(1,1) to GERM(1,1,$e^{at}$), the results of two cases show that the accuracy of the extended model is significantly improved. It shows that the extended grey action model can improve the structure of the grey model, alleviate the exponential growth and saturated S-shaped growth, weaken the dependence of the original GRM(1,1) on the saturated S-shaped data, and overcome the disadvantage of the grey model used in short-term prediction, and apply new model to medium and long-term prediction.

4. Applications

After the model test in Section 3, GERM(1,1,$e^{at}$) is applied to the representative epidemic developing countries in the world, including China, Italy, the United Kingdom and Russia. The research data on the number of all confirmed patients per day are all from the WHO [1]. The first three cases use small-sample data, and the last case uses large-sample data. In addition to the traditional GM(1,1), GRM(1,1) (NGBM(1,1)), Verhulst model, ARGM(1,1), ENGM(1,1), ONGM(1,1) and ARIMA models are added to the model for comparison. There are still two ways to compare: one is to use MAPE index; the other is curve trend chart and APE percentage chart. The curve trend chart is used to evaluate the fitting and approximation degree of the model simulation trend line and the actual data trend line. The higher the degree of fitting and approximation, the better the data fitting ability of the model is. The APE percentage comparison chart is used to evaluate the error size by measuring the area occupied by percentage of APE value of each point of each model. The larger the area proportion, the greater the error. The number of modeling data and prediction data in the four cases is shown in Table 7 . Due to the large amount of data in each case, the fitting result of each model is put into the Appendix.

• Case 1: China

Table 7.

Metrics of models in Validation Case 1.

NO.	Country	Date	Points for modeling	Points for prediction
Case 1	China	1.23-2.6	9	6
Case 2	Italy	3.10-3.21	10	2
Case 3	United Kingdom	4.11-4.25	5	10
Case 4	Russian	6.1-8.12	61	12

China is the first center for the occurrence of COVID-19 epidemic, and China immediately adopted strong measures to quickly begin to control the epidemic. In this case, eight prediction models are established based on the number of confirmed cases in the first nine days of the outbreak period, and the data of the next six days are used to test the accuracy of the models. The fitting results of the eight prediction models are shown in Table 13 in Appendix, and the comparison of MAPE values is shown in Table 8 . Using GA algorithm, the optimal parameters of GERM(1,1,$e^{at}$) are $\gamma ,\beta ,\alpha =[0.0707,0.1385,0.0416]$, and the optimal parameter of GRM (1,1) is $\gamma =0.9818$.

Table 8.

Fitting MAPE values of models in Case 1.

MAPE	GM(1,1)	Verhulst	ARGM(1,1)	ONGM(1,1)	ENGM(1,1)	ARIMA	GRM(1,1)	GERM(1,1,$e^{at}$)
MAPESIM	29.7152	43.2128	35.3292	14.6649	17.5457	72.7097	24.7328	7.7121
MAPEPRE	59.5837	55.2802	27.2007	12.1904	14.1994	10.0138	5.2691	4.2684
MAPETOT	42.5160	48.3845	31.8456	13.6044	26.7355	53.4474	16.3912	6.2362

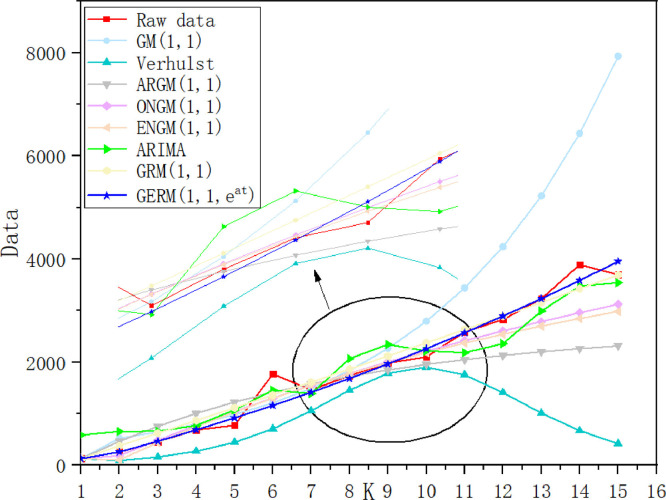
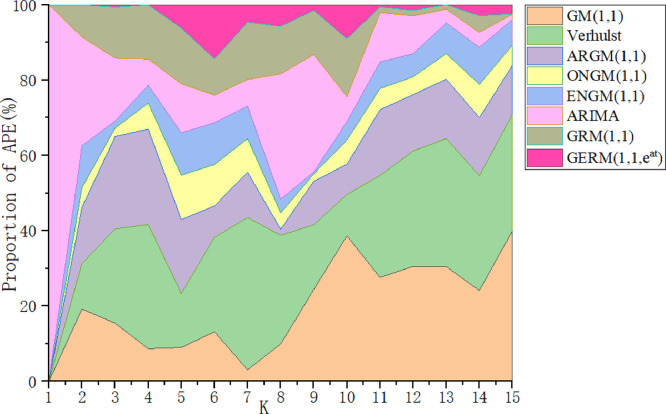
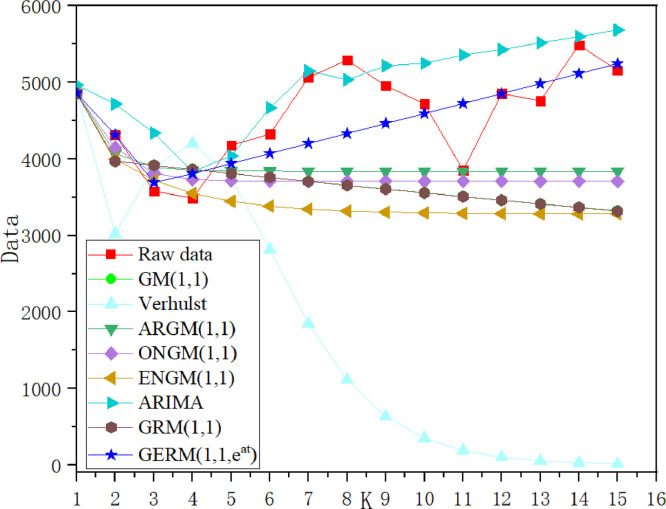
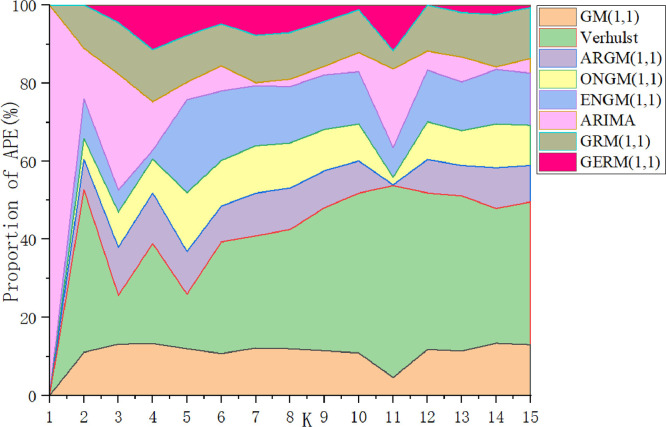
In Table 8, in the modeling stage, the MAPE_SIM of GERM(1,1,$e^{at}$) is the lowest, which is 17% higher than that of the original GRM(1,1). The two models with the largest MAPE_SIM are ARIMA and Verhulst models. In the prediction stage, the lowest MAPE_PRE is GERM(1,1,$e^{at}$), the two models with the maximum MAPE_PRE are also ARIMA and Verhulst models, which indicates that ARIMA and Verhulst models are not suitable for the prediction of epidemic situation in China. In order to show the model fitting effect from the second aspect, the results in Table 13 are transformed into curve trend chart and APE percentage chart, as shown in Fig. 5, Fig. 6 . In Fig. 5, the GERM(1,1,$e^{at}$) is the closest to the original trend line. The original GRM(1,1) basically overestimates the development of the epidemic situation, first overestimates and then underestimates the original data, Verhulst shows a single-peak trend, ENGM(1,1) and ONGM(1,1) basically underestimate the development of the epidemic situation. In Fig. 6, it is clear that ONGM (1,1) and ENGM (1,1) occupy a small area in the percentage of APE each year, indicating that the prediction error of these two models are small, while the APE percentage of GERM(1,1,$e^{at}$) is slightly larger at point 6 and point 10, and the area of other points is basically close to 0. The comparison results of the two aspects show that GERM(1,1,$e^{at}$) effectively predicts the development of the early stage of the outbreak in China.

• Case 2: Italy

Fig. 5.

the overall trend of simulation results of eight models in Case 1.

Fig. 6.

APE percentages of the eight models in Case 1.

At the beginning of the outbreak in Italy, the number of newly COVID-19 confirmed cases in a single day is close to 3500, and its mortality rate exceeded 7%. Two data made Italy an early outbreak country in Europe. If calculated in proportion to the population, the epidemic in Italy is the most severely affected country in the world at that time. The data of 10 days from March 10 to March 19 are used to build eight models, and the data from the next two days are used to test the model prediction accuracy. According to GA algorithm, the optimal parameters of GERM(1,1,$e^{at}$) are $\gamma ,\beta ,\alpha =[0.0382,-0.1587,0.2547]$, and the optimal parameter of GRM(1,1) is $\gamma =1.5625\times 10^{-4}$. The fitting results of the eight prediction models are shown in Table 14 in Appendix, and the comparison of MAPE values is shown in Table 9 .

Table 9.

Fitting MAPE values of models in Case 2.

MAPE	GM(1,1)	Verhulst	ARGM(1,1)	ONGM(1,1)	ENGM(1,1)	ARIMA	GRM(1,1)	GERM(1,1,$e^{at}$)
MAPESIM	8.3361	52.5502	14.7858	8.3953	19.0126	21.3977	8.3376	7.1304
MAPEPRE	11.7031	29.7941	21.7826	5.8776	21.9019	24.2912	11.7076	3.4857
MAPETOT	8.9483	48.4127	16.0579	7.9375	19.5379	21.9238	8.9503	6.4677

In Table 9, in the modeling stage, the MAPE_SIM of GERM(1,1,$e^{at}$) is the lowest, which is 1% higher than that of GRM(1,1). In the prediction stage, the MAPE_PRE of GERM(1,1,$e^{at}$) is the lowest, which is 8% higher than that of GRM(1,1), so the MAPE_TOT of GERM(1,1,$e^{at}$) is also the lowest. The results in Table 14 are transformed into curve trend chart and APE percentage chart, as shown in Fig. 7, Fig. 8 . In Fig. 7, the blue line is the closest to red line, that is, the line of GERM(1,1,$e^{at}$) model is the closest to the original trend line. GRM(1,1), Verhulst, ARIMA, ENGM(1,1) and ONGM(1,1) basically overestimate the development of the epidemic. In Fig. 8, the APE of Verhulst model occupies the largest area. APE of GERM(1,1,$e^{at}$) only has larger areas at points 5, 6, and 10 than other points, while other points are basically close to 0. The above results show that GERM(1,1,$e^{at}$) effectively predict the development in the early stage of the outbreak in Italy.

• Case 3: The United Kingdom

Fig. 7.

The overall trend of simulation results of eight models in Case 2.

Fig. 8.

APE percentages of the eight models in Case 2.

After the outbreak in Italy, the epidemic began to spread in Europe, and the United Kingdom was not included. The research objects of the first two cases were modeling data with a large amount of modeling data and a small amount of predicted data. Therefore, this case selects the data of 5 days from April 11 to April 15 during the outbreak period of the United Kingdom to establish the model, and the data of the last 10 days are used for model accuracy test. Based on GA algorithm, the optimal parameters of GERM(1,1,$e^{at}$) are $\gamma ,\beta ,\alpha =[0.3007,0.9993,-3.7872]$, and the optimal parameter of GRM(1,1) is $\gamma =2.3333\times 10^{-3}$. The fitting results of the eight prediction models are shown in Table 15 in Appendix, and the comparison of MAPE values is shown in Table 10 .

Table 10.

Fitting MAPE values of models in Case 3.

MAPE	GM(1,1)	Verhulst	ARGM(1,1)	ONGM(1,1)	ENGM(1,1)	ARIMA	GRM(1,1)	GERM(1,1,$e^{at}$)
MAPESIM	9.2207	17.4099	8.1942	7.1084	7.6501	9.2277	9.2222	4.4999
MAPEPRE	26.2797	84.8051	20.0258	22.7735	31.1187	10.9995	26.3003	8.9448
MAPETOT	21.4057	21.4208	16.6453	18.2976	24.4134	10.4933	21.4208	7.6748

In Table 10, in the modeling stage, the MAPE_SIM of GERM(1,1,$e^{at}$) is the lowest, which increases that of GRM(1,1) by 5 percentage points, and the highest MAPE_SIM model is Verhulst. In the prediction stage, the MAPE_PRE of GERM(1,1,$e^{at}$) is the lowest, which increases that of GRM(1,1) model by 18 percentage points. The MAPE_SIM of ARIMA model is the second, and MAPE_SIM of other models is more than 20%. Therefore, the MAPE_TOT of GERM(1,1,$e^{at}$) is also the lowest. The results in Table 15 are transformed into curve trend chart and APE percentage chart, as shown in Fig. 9, Fig. 10 . In Fig. 9, the line of GERM(1,1,$e^{at}$) is the closest to the original trend line. The trend line of ARIMA model is similar to the actual trend line, but some points are far away from the actual point. The other six models basically underestimate the development of epidemic situation. In Fig. 10, GM (1,1), ARIMA and Verhulst models have larger area of APE percentage in modeling stage, the APE percentage of ARIMA and Verhulst models are also larger in prediction stage, and APE percentage of GERM(1,1,$e^{at}$) only accounts for a large area in points 4, 7 and 11, and these of other points are close to 0. The above results show that GERM(1,1,$e^{at}$) can effectively predict the development of the outbreak period in Britain.

• Case 4: Russian

Fig. 9.

The overall trend of simulation results of eight models in Case 3.

Fig. 10.

APE percentages of the eight models in Case 3.

Up to now, the daily diagnosis of more than 5000 patients in Russia, the epidemic situation is still grim. The research objects of above three cases are small-sample data, and the last case uses large-sample data. The data of June and July are used for modeling, and the data of August are used to test the model accuracy. Base on the GA algorithm, the optimal parameters of GERM(1,1,$e^{at}$) are $\gamma ,\beta ,\alpha =[0.0064,0.6512,-0.0306]$, and the optimal parameter of GRM(1,1) is $\gamma =3.944\times 10^{-3}$. The comparison of MAPE values is shown in Table 11 , and the fitting results of the eight prediction models are shown in Table 16 in Appendix.

Table 11.

Metrics of models in Case 4.

MAPE	GM(1,1)	Verhulst	ARGM(1,1)	ONGM(1,1)	ENGM(1,1)	ARIMA	GRM(1,1)	GERM(1,1,$e^{at}$)
MAPESIM	2.8280	51.8554	3.0286	2.6521	2.6664	1.4243	2.8294	2.6248
MAPEPRE	2.7481	40.7817	3.9221	1.0399	1.8335	7.0740	2.7735	0.9023
MAPETOT	2.8149	50.0351	3.1755	2.3871	2.5295	2.3530	2.8202	2.3416

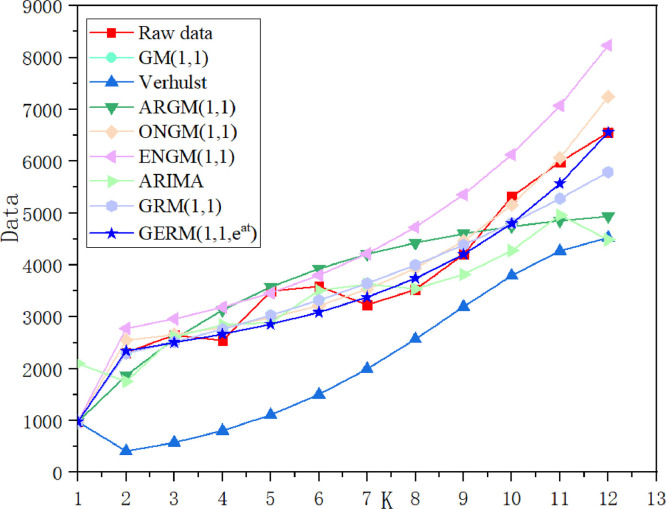
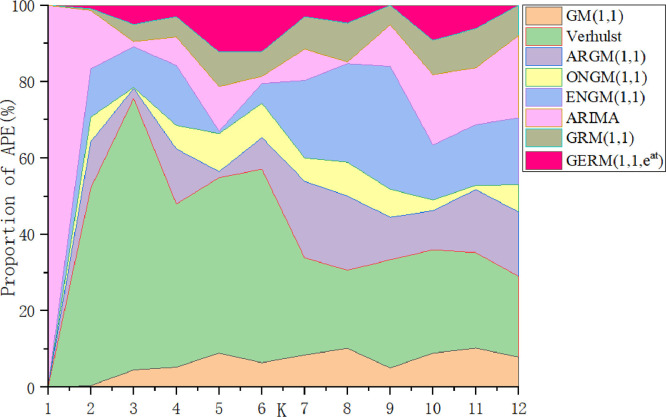
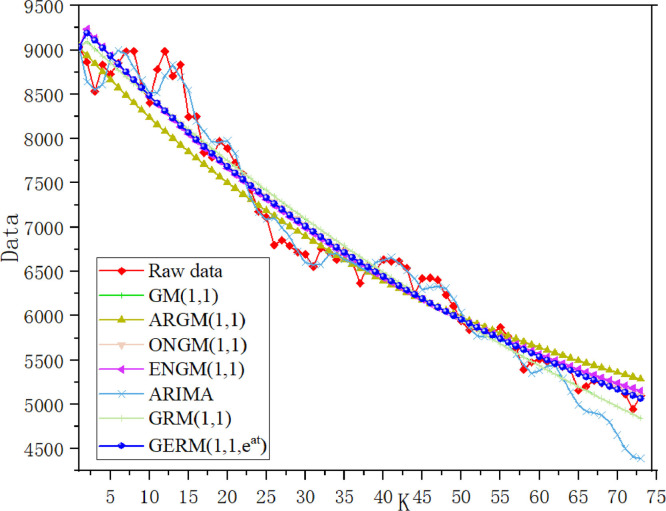
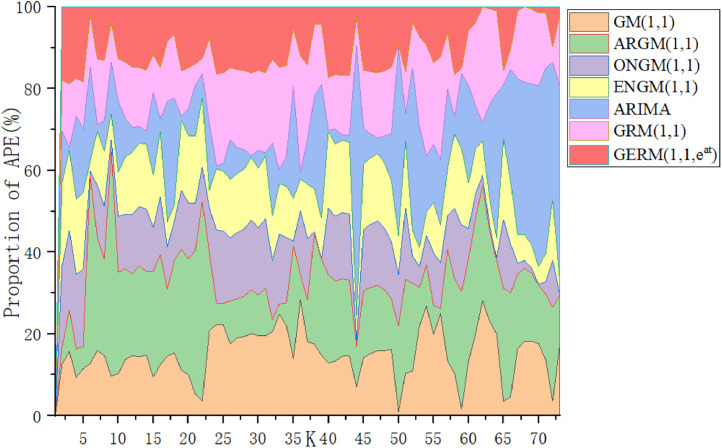
Table 11 summarizes the errors in the modeling and prediction stages. In the modeling phase, the ARIMA model has the lowest MAPE_SIM, followed by the GERM(1,1,$e^{at}$), and MAPE_SIM of Verhulst model is the largest. In the prediction phase, the MAPE_PRE of GERM(1,1,$e^{at}$) is the best, which is about 2% higher than that of original GRM(1,1). Due to the large error of Verhulst model, the graph of Verhulst model is omitted in the process of graphical fitting results. In Fig. 11 , ARIMA model has the best fitting effect in the modeling stage, while the predicted fitting line of GERM(1,1,$e^{at}$) is the closest to the actual curve, which indicates that ARIMA model is more suitable for fitting large-sample data. In Fig. 12 , in the modeling phase, the APE percentage of ARIMA model accounts for the smallest area, and other models have little difference. In the prediction phase, only two points of GERM(1,1,$e^{at}$) account for a large proportion, and other points are close to 0. The comparison results of the two perspectives show that the expanded model not only can effectively predict the daily number of confirmed patients in Russia, but also has advantages in medium and long-term prediction, which improves the disadvantage of grey model which is generally suitable for short-term prediction.

Fig. 11.

the overall trend of simulation results of eight models in Case 4.

Fig. 12.

APE percentages of the eight models in Case 4.

5. Conclusion

Due to the advantages of traditional Richards model in processing saturated S-shaped data, it has been applied to the trend prediction of various infectious diseases. Therefore, in this paper, based on the structure of traditional Richards growth model and the theory of grey differential information, the corresponding GRM(1,1) is established. Meanwhile, the grey action quantity is modified to improve the structure of GRM(1,1), and the GERM(1,1,$e^{at}$) is established. The new model weakens the dependence of the Richards model on S-shaped data. In practical cases, through the comparison with GM(1,1), ARGM(1,1), ONGM(1,1), ENGM(1,1), Verhulst and ARIMA models, GRM(1,1) (NGBM(1,1)), the fitting effect of GERM(1,1,$e^{at}$) is better than other models, that is, this model accuracy is the highest.

As mentioned in this paper, China, Italy, Britain, Russia and other places are the regions with severe epidemic situation in different periods of time, and the prediction of their infectious disease system is more complex. The priority of the GERM(1,1,$e^{at}$) over the other above models indicates that it is qualified to predict the number of daily confirmed patients of COVID-19. As COVID-19 is in a global pandemic, it is expected that the GERM(1,1,$e^{at}$) model can be applied to predict the number of confirmed cases around the world, which will be of great help to local governments to make policy decisions

As a single-variable grey model, GERM(1,1,$e^{at}$) can effectively predict the daily average number of daily confirmed patients of COVID-19. With the in-depth study of covid-19, the mechanism of virus transmission and the factors affecting virus transmission will become clear gradually. In the process of prediction, considering these factors such as temperature, population and environment will bring uncertainty to the model. Therefore, fully mining the ways of these factors affecting virus transmission, and introducing them into the GERM(1,1,$e^{at}$), and extending the GERM(1,1,$e^{at}$) to a multivariate model, the prediction effect may be further improved. How to establish multivariate GERM model is also our anticipated next main research direction.

CRediT authorship contribution statement

Xilin Luo: Software, Methodology, Visualization, Writing - original draft, Writing - review & editing, Validation, Data curation. Huiming Duan: Conceptualization, Methodology, Funding acquisition, Project administration, Resources, Supervision. Kai Xu: Investigation, Formal analysis, Validation, Data curation.

Declaration of Competing Interest

The authors declare that there is no conflict of interests regarding the publication of this paper

Appendix

See Table 12, Table 13, Table 14, Table 15, Table 16.

Table 12.

Results of three grey models in Validation Case 1.

Raw data	GM (1,1)	APE (%)	GRM (1,1)	APE (%)	GRM (1,1,)	APE (%)	Raw data	GM (1,1)	APE (%)	GRM (1,1)	APE (%)	GERM (1,1,$e^{at}$)	APE (%)
10	10.0000	0.0000	10.0000	0.0000	10.0000	0.0000	40	37.7643	-5.5893	39.7978	-0.5055	39.8225	-0.4439
11	18.9264	23.2912	9.2933	-3.073	10.2359	-0.304	41	38.6747	-5.6716	40.7426	-0.6279	40.8005	-0.4865
12	19.3826	2.0644	11.0746	-2.3283	11.3413	0.0629	42	39.607	-5.6976	41.6918	-0.7339	41.779	-0.5262
13	19.8499	-4.9464	12.6151	-2.0157	12.4385	0.1018	43	40.5618	-5.6702	42.6457	-0.8239	42.7581	-0.5625
14	20.3284	-5.5739	14.0047	-1.7336	13.5264	0.1188	44	41.5396	-5.5918	43.6048	-0.8982	43.7382	-0.5949
15	20.8185	-2.2889	15.2903	-1.3993	14.6053	0.125	45	42.541	-5.4644	44.5694	-0.9569	44.7195	-0.6233
16	21.3203	3.9993	16.4999	-0.9970	15.6757	0.1249	46	43.5665	-5.2901	45.5397	-1.0006	45.7023	-0.6471
17	21.8343	12.9983	17.6516	-0.5280	16.7382	0.1209	47	44.6168	-5.0706	46.5162	-1.0295	46.6869	-0.6662
18	22.3606	24.7247	18.7582	0.0021	17.7932	0.1143	48	45.6924	-4.8076	47.499	-1.0438	47.6735	-0.6803
19	22.8997	39.389	19.8288	0.5874	18.8409	0.1058	49	46.7939	-4.5023	48.4884	-1.044	48.6623	-0.6891
20	23.4517	17.2587	20.8704	4.3521	19.8819	-0.5905	50	47.9219	-4.1561	49.4848	-1.0303	49.6537	-0.6925
21	24.0171	14.3671	21.8884	4.2302	20.9165	-0.3977	51	49.0772	-3.7702	50.4884	-1.0031	50.6480	-0.6903
22	24.5961	11.8003	22.8869	4.0312	21.945	-0.2498	52	50.2603	-3.3456	51.4994	-0.9627	51.6452	-0.6823
23	25.1890	9.5174	23.8694	3.7801	22.9679	-0.1394	53	51.4719	-2.8832	52.5181	-0.9092	52.6458	-0.6683
24	25.7962	7.4843	24.8389	3.4953	23.9855	-0.0602	54	52.7127	-2.3838	53.5447	-0.8431	53.6499	-0.6483
25	26.4181	5.6724	25.7975	3.1902	24.9982	-0.0072	55	53.9835	-1.8482	54.5795	-0.7646	54.6579	-0.6221
26	27.055	4.0575	26.7475	2.8749	26.0063	0.0242	56	55.2849	-1.277	55.6226	-0.674	55.6699	-0.5895
27	27.7072	2.6191	27.6904	2.5569	27.0101	0.0375	57	56.6176	-0.6709	56.6743	-0.5714	56.6862	-0.5506
28	28.3751	1.3397	28.6277	2.2418	28.0101	0.036	58	57.9825	-0.0302	57.7348	-0.4572	57.7070	-0.5051
29	29.0591	0.2039	29.5608	1.9337	29.0064	0.0222	59	59.3803	0.6445	58.8044	-0.3315	58.7327	-0.4531
30	29.7597	-0.8011	30.4907	1.6358	29.9996	-0.0014	60	60.8117	1.3529	59.8832	-0.1947	59.7633	-0.3944
31	30.4771	-1.6868	31.4186	1.3503	30.9898	-0.0328	61	62.2777	2.0946	60.9714	-0.0469	60.7993	-0.3291
32	31.2118	-2.4631	32.3452	1.0788	31.9775	-0.0704	62	63.7791	2.8694	62.0693	0.1117	61.8407	-0.2569
33	31.9642	-3.1387	33.2714	0.8225	32.9628	-0.1126	63	65.3166	3.6771	63.1770	0.2809	62.8879	-0.1779
34	32.7348	-3.7213	34.198	0.5823	33.9462	-0.1581	64	66.8912	4.5174	64.2947	0.4605	63.9411	-0.0921
35	33.5239	-4.2174	35.1255	0.3586	34.928	-0.2057	65	68.5037	5.3903	65.4227	0.6503	65.0005	0.0007
36	34.3321	-4.6331	36.0547	0.1518	35.9084	-0.2545	66	70.1551	6.2956	66.5611	0.8501	66.0663	0.1005
37	35.1597	-4.9738	36.986	-0.0379	36.8877	-0.3034	67	71.8463	7.2333	67.7101	1.0599	67.1388	0.2072
38	36.0073	-5.2439	37.9199	-0.2107	37.8663	-0.3517	68	73.5783	8.2034	68.87	1.2794	68.2183	0.321
39	36.8753	-5.4479	38.8571	-0.3665	38.8445	-0.3988	69	75.3521	9.2059	70.0408	1.5084	69.3049	0.4418
70	77.1686	10.2408	71.2229	1.747	70.3988	0.5698

Table 13.

Fitting values of models in Case 1.

Date	Raw data	GM (1,1)	APE (%)	Verhulst	APE (%)	ARGM (1,1)	APE (%)	ONGM (1,1)	APE (%)
1.23	131	131.0000	0.0000	131.0000	0.0000	131	0.0000	131.0000	0.0000
1.24	261	525.4234	101.3116	94.8453	-63.6608	465.5988	78.3903	188.401	27.8157
1.25	462	647.4437	40.1393	161.5834	-65.0252	756.06	63.6494	489.2726	-5.9032
1.26	688	797.8011	15.9595	271.6218	-60.5201	1008.2059	46.5416	775.2303	-12.6788
1.27	776	983.0764	26.6851	446.4831	-42.4635	1227.0907	58.1302	1047.0131	-34.9244
1.28	1772	1211.3786	-31.6378	707.5696	-60.0694	1417.102	-20.0281	1305.3239	26.3361
1.29	1462	1492.7000	2.0999	1058.8516	-27.5751	1582.0485	8.2113	1550.8304	-6.0759
1.30	1741	1839.3533	5.6492	1455.9708	-16.3716	1725.2366	-0.9054	1784.1672	-2.4794
1.31	1984	2266.5107	14.2395	1785.2687	-10.0167	1849.5365	-6.7774	2005.9377	-1.1057
2.1	2101	2792.8680	32.9304	1905.3780	-9.3109	1957.4397	-6.8330	2216.7151	5.5076
2.2	2590	3441.4625	32.8750	1754.7511	-32.249	2051.1092	-20.8066	2417.0444	-6.6778
2.3	2827	4240.6817	50.0064	1409.742	-50.1329	2132.4226	-24.5694	2607.4435	-7.7664
2.4	3233	5225.5054	61.6302	1013.4274	-68.6537	2203.0097	-31.8587	2788.4047	-13.7518
2.5	3892	6439.0372	65.4429	671.7559	-82.7401	2264.2856	-41.8221	2960.3957	-23.9364
2.6	3697	7934.3904	114.617	421.6564	-88.5946	2317.4784	-37.3146	3123.8612	-15.5028

Date	Raw data	ENGM (1,1)	APE (%)	ARIMA	APE (%)	GRM (1,1)	APE (%)	GERM(1,1,$e^{at}$)	APE (%)
1.23	131	131.0000	0.0000	587.2736	-348.3005	131.0000	0.0000	131.0000	0.0000
1.24	261	107.9406	-58.6435	657.3624	-151.863	378.7444	45.1128	260.9996	-0.0002
1.25	462	439.9931	-4.7634	662.6214	-43.4246	624.1423	35.0957	469.4866	1.6205
1.26	688	748.3673	8.7743	775.4638	-12.7128	869.6805	26.4071	688.0390	0.0057
1.27	776	1034.7516	33.3443	1074.8507	-38.5117	1116.2213	43.8429	918.1424	18.3173
1.28	1772	1300.714	-26.5963	1459.0940	17.6584	1364.2258	-23.0121	1160.6658	-34.4997
1.29	1462	1547.7108	5.8626	1391.2421	4.8398	1613.9876	10.3959	1416.0809	-3.1408
1.30	1741	1777.0945	2.0732	2069.5928	-18.8738	1865.7134	7.1633	1684.6594	-3.2361
1.31	1984	1990.121	0.3085	2345.1462	-18.2029	2119.5596	6.8326	1966.6041	-0.8768
2.1	2101	2187.9568	4.1388	2220.4564	-5.6857	2375.6505	13.0724	2262.1216	7.6688
2.2	2590	2371.6851	-8.4291	2184.6567	15.6503	2634.0888	1.7023	2571.4581	-0.7159
2.3	2827	2542.3119	-10.0703	2361.6271	16.4617	2894.9622	2.4040	2894.9135	2.4023
2.4	3233	2700.7714	-16.4624	2993.5868	7.4053	3158.3475	-2.3091	3232.8462	-0.0048
2.5	3892	2847.9312	-26.8260	3475.7700	10.6945	3424.3133	-12.0166	3585.6721	-7.8707
2.6	3697	2984.5973	-19.2698	3542.2804	4.1850	3692.9217	-0.1103	3953.8634	6.9479

Table 14.

Fitting values of models in Case 2.

Date	Raw data	GM (1,1)	APE (%)	Verhulst	APE (%)	ARGM (1,1)	APE (%)	ONGM (1,1)	APE (%)
3.10	977	977.0000	0.0000	977.0000	0.0000	977.0000	0.0000	977.0000	0.0000
3.11	2313	2295.3639	-0.7625	411.9399	-82.1902	1868.5143	-19.2168	2551.2386	-10.3000
3.12	2651	2518.0459	-5.0152	578.7551	-78.1684	2575.0435	-2.8652	2658.438	-0.2806
3.13	2547	2762.3310	8.4543	806.3475	-68.3413	3134.9711	23.0848	2798.3715	-9.8693
3.14	3497	3030.3152	-13.3453	1110.4411	-68.2459	3578.7163	2.3368	2981.0345	14.7545
3.15	3590	3324.2975	-7.4012	1504.9561	-58.0792	3930.3864	9.4815	3219.4750	10.3210
3.16	3233	3646.8002	12.7993	1996.0261	-38.2609	4209.0865	30.1914	3530.7248	-9.2089
3.17	3526	4000.5901	13.4597	2572.7846	-27.0339	4429.9576	25.6369	3937.0168	-11.6567
3.18	4207	4388.7024	4.3191	3196.8035	-24.0123	4604.9990	9.4604	4467.3728	-6.1890
3.19	5318	4814.4671	-9.4685	3796.0134	-28.6195	4743.7201	-10.7988	5159.6764	2.9771
3.20	5986	5281.5367	-11.7685	4272.1207	-28.6315	4853.6572	-18.9165	6063.3796	1.2927
3.21	6557	5793.9186	-11.6377	4527.1791	-30.9565	4940.7828	-24.6487	7243.0346	10.4626

Date	Raw data	ENGM (1,1)	APE (%)	ARIMA	APE (%)	GRM (1,1)	APE (%)	GERM (1,1,$e^{at}$)	APE (%)
3.10	977	977.0000	0.0000	2103.8538	-115.3382	977.0000	0.0000	977.0000	0.0000
3.11	2313	2778.3139	20.1173	1753.5983	24.1851	2295.1304	-0.7726	2345.6369	1.4110
3.12	2651	2961.7041	11.7203	2612.2324	1.4624	2517.9964	-5.0171	2506.3437	-5.4567
3.13	2547	3186.8406	25.1213	2849.9128	-11.8929	2762.3603	8.4554	2669.8166	4.8220
3.14	3497	3463.2265	-0.9658	2889.2604	17.3789	3030.3800	-13.3434	2859.3663	-18.2337
3.15	3590	3802.5278	5.9200	3512.8958	2.1477	3324.3702	-7.3992	3090.2263	-13.9213
3.16	3233	4219.0666	30.5001	3633.3998	-12.3848	3646.8581	12.8011	3378.2706	4.4934
3.17	3526	4730.4249	34.1584	3543.4230	-0.4941	4000.6122	13.4604	3742.5556	6.1417
3.18	4207	5358.1871	27.3636	3819.6221	9.2079	4388.6674	4.3182	4207.0690	0.0016
3.19	5318	6128.8509	15.2473	4281.7874	19.485	4814.3521	-9.4706	4802.5537	-9.6925
3.20	5986	7074.9461	19.0126	4964.6274	17.0627	5281.3168	-11.7722	5568.7153	-6.9710
3.21	6557	8236.4073	18.1915	4490.2532	31.5197	5793.5659	-11.6430	6557.0293	0.0004

Table 15.

Fitting values of models in Case 3.

Date	Raw data	GM (1,1)	APE (%)	Verhulst	APE (%)	ARGM (1,1)	APE (%)	ONGM (1,1)	APE (%)
4.11		4858.0000	0.0000	4858.0000	0.0000	4858	0.0000	4858.0000	0.0000
4.12	4313	3969.9498	-7.9539	3021.5485	-29.9432	4072.0243	-5.5872	4146.0369	3.8712
4.13	3579	3915.9128	9.4136	3897.1178	8.8885	3892.5527	8.7609	3810.8437	-6.4779
4.14	3489	3862.6113	10.7083	4205.6223	20.5395	3851.5718	10.3919	3731.8115	-6.9593
4.15	4178	3810.0353	-8.8072	3748.9680	-10.2688	3842.2141	-8.0370	3713.1771	11.1255
4.16	4326	3758.1749	-13.1259	2813.6517	-34.9595	3840.0773	-11.2326	3708.7835	-14.2676
4.17	5065	3707.0205	-26.8110	1850.8859	-63.4573	3839.5894	-24.1937	3707.7476	-26.7967
4.18	5292	3656.5623	-30.9040	1114.2737	-78.9442	3839.478	-27.4475	3707.5033	-29.9414
4.19	4956	3606.7910	-27.2237	635.3629	-87.1799	3839.4526	-22.5292	3707.4457	-25.1928
4.20	4721	3557.6971	-24.6410	351.1143	-92.5627	3839.4468	-18.6730	3707.4322	-21.4693
4.21	3853	3509.2714	-8.9211	190.6801	-95.0511	3839.4454	-0.3518	3707.4290	-3.7781
4.22	4854	3461.5049	-28.6876	102.5734	-97.8868	3839.4451	-20.9014	3707.4282	-23.6212
4.23	4760	3414.3886	-28.2691	54.8958	-98.8467	3839.4451	-19.3394	3707.4281	-22.1129
4.24	5487	3367.9136	-38.6201	29.2989	-99.4660	3839.445	-30.0265	3707.4282	-32.4325
4.25	5158	3322.0712	-35.5938	15.6144	-99.6973	3839.445	-25.5633	3707.4283	-28.1228

Date	Raw data	ENGM (1,1)	APE (%)	ARIMA	APE (%)	GRM (1,1)	APE (%)	GERM(1,1,$e^{at}$)	APE (%)
4.11	4858	4858.0000	0.0000	4965.9742	-2.2226	4858.0000	0.0000	4858.0000	0.0000
4.12	4313	3998.2368	-7.2980	4717.4428	-9.3773	3969.8426	-7.9564	4313.0979	0.0023
4.13	3579	3722.3409	4.0051	4339.0877	-21.2374	3915.9602	9.4149	3692.1102	3.1604
4.14	3489	3552.3716	1.8163	3836.821	-9.9691	3862.6518	10.7094	3807.9261	9.1409
4.15	4178	3447.6599	-17.4806	4038.7789	3.3322	3809.991	-8.8083	3940.0159	-5.6961
4.16	4326	3383.1509	-21.7949	4667.2344	-7.8880	3758.0015	-13.1299	4071.6967	-5.8785
4.17	5065	3343.4092	-33.9899	5150.3372	-1.6848	3706.6903	-26.8176	4202.7668	-17.0234
4.18	5292	3318.9259	-37.2841	5034.3642	4.8684	3656.0579	-30.9135	4333.3862	-18.1144
4.19	4956	3303.8426	-33.3365	5216.7338	-5.2610	3606.1007	-27.2377	4463.7041	-9.9333
4.20	4721	3294.5504	-30.2150	5250.5274	-11.2164	3556.8135	-24.6597	4593.8537	-2.6932
4.21	3853	3288.8257	-14.6425	5358.3126	-39.0686	3508.1901	-8.9491	4723.9543	22.6046
4.22	4854	3285.2990	-32.3177	5429.2496	-11.8510	3460.2232	-28.714	4854.1137	0.0023
4.23	4760	3283.1263	-31.0268	5518.5372	-15.9357	3412.9056	-28.3003	4984.4298	4.7149
4.24	5487	3281.7878	-40.1898	5598.6861	-2.0355	3366.2295	-38.6508	5114.9921	-6.7798
4.25	5158	3280.9632	-36.3908	5683.3861	-10.1858	3320.1870	-35.6303	5245.8824	1.7038

Table 16.

Fitting values of models in Case 4.

Date	Raw data	GM (1,1)	APE (%)	Verhulst	APE (%)	ARGM (1,1)	APE (%)	ONGM (1,1)	APE (%)
6.1	9035	9035.0000	0.0000	9035.0000	0.0000	9035.0000	0.0000	9035.0000	0.0000
6.2	8863	9094.4356	2.6113	654.3997	-92.6165	8939.7883	0.8664	9223.4489	-4.0669
6.3	8536	9014.1475	5.6015	700.7504	-91.7906	8846.3892	3.6362	9127.1391	-6.9252
6.4	8831	8934.5682	1.1728	750.2275	-91.5046	8754.7682	-0.8632	9032.3510	-2.2800
6.5	8726	8855.6914	1.4863	803.0186	-90.7974	8664.8914	-0.7003	8939.0605	-2.4417
6.6	8855	8777.511	-0.8751	859.3189	-90.2957	8576.7257	-3.1426	8847.2440	0.0876
6.7	8984	8700.0208	-3.1609	919.3312	-89.7670	8490.2384	-5.4960	8756.8781	2.5281
6.8	8985	8623.2147	-4.0265	983.2653	-89.0566	8405.3976	-6.4508	8667.9399	3.5288
6.9	8595	8547.0867	-0.5575	1051.3379	-87.768	8322.1720	-3.1743	8580.4070	0.1698
6.10	8404	8471.6307	0.8047	1123.7713	-86.6281	8240.5309	-1.9451	8494.2570	-1.0740
6.11	8779	8396.8409	-4.3531	1200.7932	-86.3220	8160.4439	-7.0459	8409.4682	4.2093
6.12	8987	8322.7113	-7.3917	1282.6355	-85.7279	8081.8817	-10.0714	8326.0190	7.3549
6.13	8706	8249.2362	-5.2465	1369.5327	-84.2691	8004.8151	-8.0540	8243.8882	5.3080
6.14	8835	8176.4098	-7.4543	1461.7209	-83.4553	7929.2156	-10.2522	8163.0551	7.6055
6.15	8246	8104.2262	-1.7193	1559.4357	-81.0886	7855.0554	-4.7410	8083.4991	1.9707
6.16	8248	8032.6800	-2.6106	1662.9105	-79.8386	7782.3070	-5.6461	8005.2001	2.9437
6.17	7843	7961.7653	1.5143	1772.3734	-77.4018	7710.9436	-1.6837	7928.1381	-1.0855
6.18	7790	7891.4767	1.3027	1888.0453	-75.7632	7640.9387	-1.9135	7852.2937	-0.7997
6.19	7972	7821.8087	-1.8840	2010.1361	-74.7850	7572.2666	-5.0142	7777.6476	2.4379
6.20	7889	7752.7557	-1.7270	2138.8415	-72.8883	7504.9019	-4.8688	7704.1809	2.3427
6.21	7728	7684.3123	-0.5653	2274.339	-70.5701	7438.8196	-3.7420	7631.8750	1.2439
6.22	7600	7616.4731	0.2168	2416.7834	-68.2002	7373.9953	-2.9737	7560.7114	0.5170
6.23	7425	7549.2329	1.6732	2566.3021	-65.4370	7310.4052	-1.5434	7490.6722	-0.8845
6.24	7176	7482.5862	4.2724	2722.9899	-62.0542	7248.0256	1.0037	7421.7396	-3.4245
6.25	7113	7416.5280	4.2672	2886.9034	-59.4137	7186.8336	1.0380	7353.8961	-3.3867
6.26	6800	7351.0529	8.1037	3058.0546	-55.0286	7126.8066	4.8060	7287.1245	-7.1636
6.27	6852	7286.1558	6.3362	3236.4050	-52.7670	7067.9223	3.1512	7221.4078	-5.3912
6.28	6791	7221.8317	6.3442	3421.8589	-49.6119	7010.1591	3.2272	7156.7294	-5.3855
6.29	6719	7158.0754	6.5348	3614.2566	-46.2084	6953.4955	3.4900	7093.0730	-5.5674
6.30	6693	7094.8820	6.0045	3813.3674	-43.0245	6897.9106	3.0616	7030.4223	-5.0414
7.1	6556	7032.2465	7.2643	4018.8832	-38.6992	6843.3840	4.3835	6968.7614	-6.2959
7.2	6760	6970.1640	3.1089	4230.4116	-37.4199	6789.8954	0.4422	6908.0748	-2.1905
7.3	6718	6908.6295	2.8376	4447.4702	-33.7977	6737.4251	0.2892	6848.3469	-1.9403
7.4	6632	6847.6383	3.2515	4669.4810	-29.5917	6685.9538	0.8135	6789.5628	-2.3758
7.5	6736	6787.1855	0.7599	4895.7661	-27.3194	6635.4623	-1.4925	6731.7074	0.0637
7.6	6611	6727.2664	1.7587	5125.5437	-22.4695	6585.9320	-0.3792	6674.7661	-0.9645
7.7	6368	6667.8763	4.7091	5357.9271	-15.8617	6537.3447	2.6593	6618.7245	-3.9373
7.8	6562	6609.0105	0.7164	5591.9235	-14.7832	6489.6824	-1.1021	6563.5682	-0.0239
7.9	6509	6550.6644	0.6401	5826.436	-10.4865	6442.9275	-1.0151	6509.2835	-0.0044
7.10	6635	6492.8334	-2.1427	6060.2677	-8.6621	6397.0626	-3.5861	6455.8564	2.7000
7.11	6611	6435.5129	-2.6545	6292.1274	-4.8234	6352.0709	-3.9166	6403.2734	3.1421
7.12	6615	6378.6985	-3.5722	6520.6389	-1.4265	6307.9358	-4.6419	6351.5213	3.983
7.13	6537	6322.3857	-3.2831	6744.3521	3.1720	6264.6409	-4.1664	6300.5867	3.6165
7.14	6248	6266.5700	0.2972	6961.7574	11.4238	6222.1702	-0.4134	6250.457	-0.0393
7.15	6422	6211.2470	-3.2817	7171.3023	11.6677	6180.508	-3.7604	6201.1192	3.4394
7.16	6428	6156.4125	-4.2251	7371.4112	14.6766	6139.6390	-4.4860	6152.5610	4.2850
7.17	6406	6102.0620	-4.7446	7560.5062	18.0223	6099.5481	-4.7838	6104.7700	4.7023
7.18	6234	6048.1914	-2.9806	7737.0309	24.1102	6060.2203	-2.7876	6057.734	2.8275
7.19	6109	5994.7963	-1.8694	7899.4753	29.3088	6021.6413	-1.4300	6011.4413	1.5970
7.20	5940	5941.8727	0.0315	8046.4004	35.4613	5983.7968	0.7373	5965.8799	-0.4357
7.21	5842	5889.4162	0.8116	8176.4646	39.9600	5946.6727	1.7917	5921.0383	-1.3529
7.22	5862	5837.4229	-0.4193	8288.4482	41.3928	5910.2553	0.8232	5876.9053	-0.2543
7.23	5848	5785.8886	-1.0621	8381.2769	43.3187	5874.5313	0.4537	5833.4695	0.2485
7.24	5811	5734.8092	-1.3111	8454.0434	45.4835	5839.4874	0.4902	5790.7200	0.3490
7.25	5871	5684.1808	-3.1821	8506.0257	44.8821	5805.1106	-1.1223	5748.6459	2.0840
7.26	5765	5633.9993	-2.2723	8536.7023	48.0781	5771.3883	0.1108	5707.2366	1.0020
7.27	5635	5584.2609	-0.9004	8545.7630	51.6551	5738.3079	1.8333	5666.4815	-0.5587
7.28	5395	5534.9615	2.5943	8533.1161	58.1671	5705.8574	5.7620	5626.3703	-4.2886
7.29	5475	5486.0974	0.2027	8498.8897	55.2309	5674.0246	3.6352	5586.8929	-2.0437
7.30	5509	5437.6647	-1.2949	8443.4295	53.2661	5642.7978	2.4287	5548.0392	-0.7086
7.31	5482	5389.6595	-1.6844	8367.2909	52.6321	5612.1655	2.3744	5509.7993	-0.5071
8.1	5462	5342.0782	-2.1956	8271.2278	51.4322	5582.1164	2.1991	5472.1637	0.1861
8.2	5427	5294.9169	-2.4338	8156.1765	50.2889	5552.6393	2.3151	5435.1226	0.1497
8.3	5394	5248.1719	-2.7035	8023.2368	48.7437	5523.7235	2.4050	5398.6668	0.0865
8.4	5159	5201.8397	0.8304	7873.6503	52.6197	5495.3581	6.5198	5362.787	3.9501
8.5	5204	5155.9165	-0.9240	7708.7764	48.1318	5467.5327	5.0640	5327.4741	2.3727
8.6	5267	5110.3986	-2.9733	7530.0675	42.9669	5440.2370	3.2891	5292.7191	0.4883
8.7	5241	5065.2827	-3.3527	7339.0432	40.0314	5413.4610	3.2906	5258.5132	0.3342
8.8	5212	5020.5650	-3.6730	7137.2651	36.9391	5387.1948	3.3614	5224.8478	0.2465
8.9	5189	4976.2421	-4.1002	6926.3122	33.4807	5361.4286	3.3230	5191.7142	0.0523
8.10	5118	4932.3105	-3.6282	6707.7578	31.0621	5336.1529	4.2625	5159.1042	0.8031
8.11	4945	4888.7668	-1.1372	6483.1485	31.1051	5311.3584	7.4087	5127.0094	3.6807
8.12	5102	4845.6075	-5.0253	6253.9852	22.5791	5287.0359	3.6267	5095.4216	-0.1289
(continued on next page)

Table 16.

(continued)

Date	Raw data	ENGM (1,1)	APE (%)	ARIMA	APE (%)	GRM (1,1)	APE (%)	GERM(1,1,$e^{at}$)	APE (%)
6.1	9035	9035.0000	0.0000	9035.0000	0.0000	9035.0000	0.0000	9035.0000	0.0000
6.2	8863	9234.8451	4.1955	8638.5028	2.5330	9089.6062	2.5568	9191.9322	3.7113
6.3	8536	9133.6364	7.0014	8556.2779	-0.2376	9011.0582	5.5653	9111.4905	6.7419
6.4	8831	9034.2442	2.3015	8606.9425	2.5372	8932.5335	1.1497	9024.1491	2.1872
6.5	8726	8936.6359	2.4139	8902.1140	-2.0183	8854.3859	1.4713	8934.3398	2.3876
6.6	8855	8840.7795	-0.1606	8995.2505	-1.5839	8776.7431	-0.8838	8843.8336	-0.1261
6.7	8984	8746.6435	-2.642	8955.4222	0.3181	8699.6642	-3.1649	8753.5069	-2.5656
6.8	8985	8654.1971	-3.6817	8802.5761	2.0303	8623.1798	-4.0269	8663.8463	-3.5743
6.9	8595	8563.4098	-0.3675	8657.6387	-0.7288	8547.3069	-0.5549	8575.1412	-0.2311
6.10	8404	8474.2521	0.8359	8518.8256	-1.3663	8472.0546	0.8098	8487.5701	0.9944
6.11	8779	8386.6945	-4.4687	8514.8579	3.0088	8397.4278	-4.3464	8401.2449	-4.3029
6.12	8987	8300.7084	-7.6365	8709.5847	3.0869	8323.4283	-7.3837	8316.2348	-7.4637
6.13	8706	8216.2656	-5.6253	8833.3304	-1.4626	8250.056	-5.2371	8232.5809	-5.4378
6.14	8835	8133.3383	-7.9418	8686.9944	1.6752	8177.3098	-7.4441	8150.3051	-7.7498
6.15	8246	8051.8995	-2.3539	8548.7040	-3.6709	8105.1874	-1.7076	8069.4156	-2.1415
6.16	8248	7971.9223	-3.3472	8195.0858	0.6415	8033.686	-2.5984	7989.911	-3.1291
6.17	7843	7893.3805	0.6424	8082.0461	-3.0479	7962.8022	1.5275	7911.783	0.8770
6.18	7790	7816.2484	0.3369	7962.3699	-2.2127	7892.5324	1.3162	7835.0179	0.5779
6.19	7972	7740.5006	-2.9039	7958.7017	0.1668	7822.8725	-1.8706	7759.5986	-2.6643
6.20	7889	7666.1124	-2.8253	7978.0067	-1.1282	7753.8186	-1.7135	7685.505	-2.5795
6.21	7728	7593.0593	-1.7461	7831.0397	-1.3333	7685.3662	-0.5517	7612.715	-1.4918
6.22	7600	7521.3173	-1.0353	7573.155	0.3532	7617.511	0.2304	7541.2051	-0.7736
6.23	7425	7450.8630	0.3483	7327.3437	1.3152	7550.2484	1.6868	7470.9509	0.6189
6.24	7176	7381.6732	2.8661	7165.6632	0.1440	7483.5740	4.2861	7401.9272	3.1484
6.25	7113	7313.7252	2.8219	7087.4427	0.3593	7417.4830	4.2807	7334.1083	3.1085
6.26	6800	7246.9967	6.5735	7104.7868	-4.4822	7351.9709	8.1172	7267.4685	6.8745
6.27	6852	7181.4659	4.8083	6995.3065	-2.0915	7287.0330	6.3490	7201.982	5.1077
6.28	6791	7117.1112	4.8021	6893.7525	-1.5131	7222.6646	6.3564	7137.6229	5.1042
6.29	6719	7053.9116	4.9845	6729.6816	-0.1590	7158.8611	6.5465	7074.3657	5.2890
6.30	6693	6991.8462	4.4651	6601.8851	1.3613	7095.6178	6.0155	7012.185	4.7689
7.1	6556	6930.8948	5.7183	6574.7506	-0.2860	7032.9300	7.2747	6951.0558	6.0259
7.2	6760	6871.0374	1.6426	6577.7312	2.6963	6970.7930	3.1182	6890.9534	1.9372
7.3	6718	6812.2543	1.4030	6690.4528	0.4101	6909.2024	2.8461	6831.8536	1.6948
7.4	6632	6754.5262	1.8475	6703.4529	-1.0774	6848.1534	3.2592	6773.7325	2.1371
7.5	6736	6697.8342	-0.5666	6635.8891	1.4862	6787.6414	0.7666	6716.5668	-0.2885
7.6	6611	6642.1597	0.4713	6604.6195	0.0965	6727.6619	1.7647	6660.3336	0.7462
7.7	6368	6587.4845	3.4467	6552.5218	-2.8976	6668.2104	4.7144	6605.0105	3.7219
7.8	6562	6533.7905	-0.4299	6501.1837	0.9268	6609.2823	0.7205	6550.5755	-0.1741
7.9	6509	6481.0603	-0.4292	6601.0316	-1.4139	6550.8731	0.6433	6497.0073	-0.1842
7.10	6635	6429.2765	-3.1006	6630.2764	0.0712	6492.9784	-2.1405	6444.2848	-2.8744
7.11	6611	6378.4221	-3.5180	6659.8756	-0.7393	6435.5937	-2.6532	6392.3876	-3.3068
7.12	6615	6328.4804	-4.3314	6594.5593	0.3090	6378.7147	-3.5720	6341.2959	-4.1376
7.13	6537	6279.4351	-3.9401	6510.4546	0.4061	6322.3369	-3.2838	6290.9901	-3.7633
7.14	6248	6231.2700	-0.2678	6422.2844	-2.7894	6266.4561	0.2954	6241.4512	-0.1048
7.15	6422	6183.9694	-3.7065	6293.6007	1.9994	6211.0679	-3.2845	6192.6608	-3.5711
7.16	6428	6137.5178	-4.519	6322.0877	1.6477	6156.1681	-4.2289	6144.6008	-4.4088
7.17	6406	6091.8998	-4.9032	6331.6564	1.1605	6101.7524	-4.7494	6097.2538	-4.8196
7.18	6234	6047.1007	-2.9981	6311.2151	-1.2386	6047.8166	-2.9866	6050.6025	-2.9419
7.19	6109	6003.1055	-1.7334	6190.6704	-1.3369	5994.3565	-1.8766	6004.6303	-1.7085
7.20	5940	5959.9000	0.335	6035.7108	-1.6113	5941.3680	0.0230	5959.3210	0.3253
7.21	5842	5917.4700	1.2919	5871.3449	-0.5023	5888.8469	0.8019	5914.6589	1.2437
7.22	5862	5875.8014	0.2354	5772.164	1.5325	5836.7893	-0.4301	5870.6284	0.1472
7.23	5848	5834.8808	-0.2243	5765.2549	1.4149	5785.191	-1.0740	5827.2148	-0.3554
7.24	5811	5794.6946	-0.2806	5772.1398	0.6687	5734.048	-1.3242	5784.4034	-0.4577
7.25	5871	5755.2296	-1.9719	5736.9861	2.2826	5683.3564	-3.1961	5742.1800	-2.1942
7.26	5765	5716.473	-0.8418	5681.5056	1.4483	5633.1122	-2.2877	5700.5309	-1.1183
7.27	5635	5678.4119	0.7704	5561.0200	1.3129	5583.3115	-0.9173	5659.4427	0.4338
7.28	5395	5641.034	4.5604	5452.0088	-1.0567	5533.9504	2.5755	5618.9023	4.1502
7.29	5475	5604.327	2.3621	5349.1247	2.2991	5485.025	0.1831	5578.8970	1.8977
7.30	5509	5568.2787	1.0760	5381.4724	2.3149	5436.5316	-1.3155	5539.4146	0.5521
7.31	5482	5532.8775	0.9281	5433.6295	0.8824	5388.4663	-1.7062	5500.4429	0.3364
8.1	5462	5498.1116	0.6611	5443.4267	0.3400	5340.8254	-2.2185	5461.9703	-0.0005
8.2	5427	5463.9697	0.6812	5294.0196	2.4503	5293.6051	-2.4580	5423.9855	-0.0555
8.3	5394	5430.4406	0.6756	5137.6747	4.7520	5246.8019	-2.7289	5386.4774	-0.1395
8.4	5159	5397.5133	4.6232	4995.8605	3.1622	5200.4119	0.8027	5349.4352	3.6913
8.5	5204	5365.1769	3.0972	4921.6525	5.4256	5154.4317	-0.9525	5312.8486	2.0916
8.6	5267	5333.4209	1.2611	4903.7844	6.8961	5108.8575	-3.0025	5276.7073	0.1843
8.7	5241	5302.2349	1.1684	4881.3277	6.8627	5063.6858	-3.3832	5241.0015	0.0000
8.8	5212	5271.6086	1.1437	4798.975	7.9245	5018.9132	-3.7047	5205.7216	-0.1205
8.9	5189	5241.5320	1.0124	4655.2219	10.2867	4974.536	-4.1331	5170.8582	-0.3496
8.10	5118	5211.9952	1.8366	4503.7050	12.0026	4930.5507	-3.6625	5136.4022	0.3596
8.11	4945	5182.9885	4.8127	4408.3534	10.8523	4886.9541	-1.1738	5102.3448	3.1819
8.12	5102	5154.5024	1.0291	4391.1505	13.9328	4843.7425	-5.0619	5068.6775	-0.6531