Assessing and controlling infection risk with Wells-Riley model and spatial flow impact factor (SFIF)

Abstract

The ongoing COVID-19 epidemic has spread worldwide since December 2019. Effective use of engineering controls can prevent its spread and thereby reduce its impact. As airborne transmission is an important mode of infectious respiratory disease transmission, mathematical models of airborne infection are needed to develop effective engineering control. We developed a new approach to obtain the spatial distribution for the probability of infection (PI) by combining the spatial flow impact factor (SFIF) method with the Wells-Riley model. Our method can be combined with the anti-problem approach, in order to determine the optimized arrangement of people and/or air purifiers in a confined space beyond the ability of previous methods. This method was validated by a CFD-integrated method, and an illustrative example is presented. We think our method can be helpful in controlling infection risk and making the best use of the space and equipment in built environments, which is important for preventing the spread of COVID-19 and other infectious respiratory diseases, and promoting the development of sustainable cities and society.

1. Introduction

Lower respiratory infections are a leading cause of infection mortality around the world (Troeger et al., 2017). In this century, considerable morbidity and mortality have been caused by infectious respiratory diseases such as SARS (severe acute respiratory syndrome) (Yu et al., 2004) and MERS (Middle East respiratory syndrome) (Zumla, Hui, & Perlman, 2015). As the most serious lower respiratory infection since the Spanish influenza of 1818, the pandemic of Coronavirus Disease 2019 (COVID-19) has impacted more than 200 countries and territories in the world, infecting more than 78.6 million people and causing over 1.74 million deaths as of Dec. 26, 2020. (https://covid19.who.int/, visiting at 9:00 on Dec.26, 2020 Beijing Time)

Pandemics will continue to pose a great challenge to cities and societies. Since it is likely that there are not effective treatments or vaccine for a new pandemic, it is possible to use engineering methods to prevent its spread in the physical and built environment. Most respiratory infection disease transmission occurs in indoor environments (Morawska & Milton, 2020), indicating the important role played by air flow in a confined environment. Until recently, the World Health Organization (WHO) regarded the theory of “contact” and “droplets” as the two major transmission routes of SARS-CoV-2 (WHO, 2020a,2020b). However, consistent with recent updating of transmission mechanisms (Morawska et al., 2020), the National Health Commission of the People’s Republic of China notes that the primary mode of the SARS-CoV-2 virus is airborne by virus-laden aerosols from human breath (China NHC, 2020). It follows that transmission occurs mainly in relatively confined environments. Morawska et al. (2020) concluded that engineering controls targeting airborne transmission should play a major role in the overall strategy to curb the spread of COVID-19 indoors. For this purpose, it is imperative to understand the transmission characteristics and influencing factors well. Mathematical models of airborne infection are needed for different modes of engineering control. The most classic model to quantitatively assess airborne infection risk is the Wells-Riley model, proposed by Riley, Murphy, and Riley (1978) using data from a measles outbreak in 1974.

The Wells–Riley model has been extensively employed in many studies on airborne infectious disease transmission. For example, using the Wells–Riley model, Escombe et al. (2007) demonstrated that some building factors (particularly the ventilation rate) are important removal mechanisms for airborne infectious agents. Gao, Niu, Perino, and Heiselberg (2009) investigated the airborne transmission of infection between flats in high-rise residential buildings. Gupta, Lin, and Chen (2012) adopted a 4-h airline flight case as an example to analyze the infection risk from influenza and the protective effect of N95 masks using exhalation and inhalation models. Noakes, Beggs, Sleigh, and Kerr (2006) used the Wells-Riley model in conjunction with the Susceptible, Exposed (infected, but not yet infectious), Infectious (now can infect others), Removed (SEIR) epidemic model to simulate the transmission dynamics of airborne infectious diseases in ventilated rooms. They assessed the long-term impact of infection control measures and identified the key corresponding environmental factors. Liao, Lin, and Cheng (2013) linked the Wells-Riley model and competing-risks model (Brookmeyer, Johnson, & Bollinger, 2003) to evaluate the effectiveness of enhanced medical protective measures and engineering control measures against respiratory infections. However, there are several limitations in the Wells-Riley model and the models based on it, in particular, the assumption that the air in a confined space is in steady state and is fully mixed, which tends to not be true for many situations.

To overcome this limitation of the Wells-Riley model, many modifications have been made. Rudnick and Milton (2003) derived an alternative equation to incorporate a transient-state condition. They used CO₂ concentration as an indicator for exposure to exhaled-breath, and the exhaled air volume fraction to estimate the number of quanta that susceptible people are exposed to. Nevertheless, their model still adopts the well-mixed assumption. To obtain spatial variation of infection risk, Ko, Thompson, and Nardell (2004) divided a commercial airliner into multiple cabins, such that the degree of exposure to infectious agents and the level of infection risk vary from cabin to cabin. However, this approach is difficult to extrapolate to other premises and moreover, they ignore the possible differences among people in different locations of the same cabin. By means of integrating the Wells–Riley equation into CFD, Qian, Li, Nielsen, and Huang (2009) developed a new mathematical model to predict the spatial distribution of infection risk of airborne transmitted diseases. While this model is confined to circumstances in which the susceptible stay mostly in the same location in an enclosed space during the infectious period, its demand on computing time and computing power is high. Sun and Zhai (2020) improved the Wells-Riley model by introducing a distance index and a ventilation index to quantify the impacts of social distance and ventilation effectiveness on the probability of infection. We shall refer to this model as the Sun-Zhai model and validate it with an existing case, showing that it has acceptable accuracy. However, their method does not account for the location of the infectors, and cannot obtain the spatial distribution of PI to optimize position arrangement of people in a confined space.

The probability of infection depends on the exposure dose of a susceptible person, which is determined by the flow field and location of infected and non-infected people in the air flow field of the confined space. No theoretical models in the literature have as yet considered all those impacting factors. In principle, the spatial distribution of PI can be quite accurately predicted by using a CFD-integrated method for given people’s locations and the air flow field. When the location of people (infected and/or exposed) can change, this method cannot optimize the position arrangements of people and facilities (e.g. air purifiers) in the confined space. This is because it is almost impossible to find the most optimized arrangement in the almost infinite number of possible arrangements.

The concept of spatial flow influence factors (SFIF) was put forward by Zhang, Li, Wang, Deng, and Qian (2006). SFIF provided an insight into steady-state airflow field structure and characteristics. The concept is based on the assumption that the pollutant concentration field influence on airflow velocity field is negligible (can be expressed by SFIF matrix). For a given indoor airflow and given sources of pollution (e.g. VOCs, viral aerosol), the influence of a pollution source from a given location on the concentrations of all points in a confined space can conveniently be calculated by using the SFIF matrix. Wang, Tao, Lu, and Wang (2013) developed a method to identify the potential contaminant sources in buildings based on the SFIF method.

The purpose of this paper is to develop a novel approach to assess the spatial distribution of PI and provide guidance to optimize the locations of people (infected and exposed), and facilities (e.g. air purifiers) in a confined space, beyond the ability of previous approaches. Our method can help to assess and control infection risk in built environment and make the best use of space and medical resources so as to create a sustainable built environment for epidemic prevention.

2. Methods

2.1. Existing models revisited

2.1.1. Wells-Riley model

The Wells–Riley equation is based on the concept of a ‘quantum of infection’. A quantum is defined as the number of infectious airborne particles required to infect a person. It may consist of one or more airborne particles which are assumed to be randomly distributed throughout the air of confined spaces. Based on a Poisson distribution, the probability for a susceptible person to be infected by a quantum is 63.2 %. (Riley et al., 1978).

The equation is as follows:

$$P=\frac{C}{S}=1-\exp \left(-\frac{Iqpt}{Q}\right)$$ (1)

Where P is the probability of infection, C is the number of infection cases, S is the number of susceptibles, I is the number of infectors, q is the quanta generation rate (quanta/h), p is the pulmonary ventilation rate for a person (m³/h), t is the exposure time interval (h), and Q is the room outdoor ventilation rate (m³/h). It should be noted that the quanta generation rate, q, cannot be directly obtained, but must be backward calculated from cases in an outbreak.

As this model can make assessment quickly and does not require interspecies extrapolation of infectivity, it is extensively applied for quantitative infection risk assessment of infectious diseases in indoor premises. However, the Wells-Riley model was based on several simple assumptions. Concretely, it implies that the probability of infection is uniform within one confined space and that the ventilation and number of infectors are constant during the entire duration, and that the biologic decay of airborne infectious pathogens together with elimination of infectious particles caused by filtration and deposition is negligible (Riley et al., 1978).

As was mentioned in the Introduction, Rudnick and Milton (2003) proposed a modified Wells–Riley equation using the exhaled air volume fraction to estimate the number of quanta that a susceptible person is exposed to, but their modified equation still adopted the well-mixed assumption that the probability of infection is uniform within a confined space. The Rudnick and Milton equation is:

$$P=1-\exp \left(\frac{\overline{f}Iqt}{n}\right)$$ (2)

where $\overline{f}$ is the average volume fraction of room air that is exhaled breath and n is the total number of people in the premises.

2.1.2. CFD-integrated model

The CFD-integrated Wells-Riley model was developed from many researchers’ work (Gupta et al., 2012; Qian et al., 2009; Yan, Li, Shang, & Tu, 2017). There are two different modes, with one using a Eulerian-based approach and the other a Lagrangian-based approach.

In the Eulerian-based approach, the airflow field is solved using the incompressible Navier-Stokes (N-S) equation and the contaminant transport is determined by the governing equation.

$$\frac{\partial \varphi }{\partial \tau }+\nabla •\left(\rho \varphi v-{\Gamma }_{\varphi }\nabla \varphi \right)=S_{\varphi }$$ (3)

where ϕ is contaminant concentration, τ is time, ρ is air density, v is air velocity vector, Γ_ϕ is the diffusion coefficient, and S_ϕ is the mass flow rate of source per unit volume. Qian et al. (2009) integrated the decay of airborne organisms into Eq. (3) and made the calculation results more consistent with real situations.

In the Lagrangian-based approach, the airflow field was solved using the incompressible Navier-Stokes (N-S) equation as well. The Lagrangian approach is used to calculate fine particle motion and deposition and the particle source in-cell (PSI-C) scheme is applied to correlate the concentration with the trajectories on a computational cell basis (Yan et al., 2017):

$${\overline{C}}_j=\left(\frac{M\sum _{i=1}^n\text{d}{t}_{ij}}{V_j}\right)$$ (4)

where M is the mass flow rate of each trajectory, V is the volume of a computational cell for use in concentration calculations, dt is the particle residence time, and the subscripts (i,j) represent the ith trajectory and the jth cell, respectively.

Finally, using the calculated susceptible inhaled contaminant concentration, each susceptible's infection risk can be determined as (Qian 2009; You, Lin, Wei, & Chen, 2019):

$$P_i=1-\exp \left(-C_{q,i}pt\right)$$ (5)

where P_i is the infection risk for the susceptible i, C_q,i is the the susceptible i inhaled contaminant concentration, p is the susceptible's breathing flow rate, and t is the exposure duration.

2.2. Improved approach by combining the Wells-Riley model and SFIF matrix

2.2.1. SFIF matrix

The contaminant concentration equation for a given space with steady airflow can be written as follows:

$$\nabla \cdot \left({\rho }_A\text{v}-{\Gamma }_A\nabla {\rho }_A\right)=S_i$$ (6)

where v is velocity vector, S_i is the emission rate density of the ith contaminant source (i = 1, 2, 3, …), ρ_A and Γ_A are the mass density and the mass transport coefficients of contaminant A in air.

Tracer gas is a suitable surrogate of exhaled droplet nuclei for studying airborne transmission in the built environment (Ai, Mak, Gao, & Niu, 2020). Indoor air pollutants and exhaled droplets (or droplet nuclei, the residual of evaporated droplets) are usually a very small fraction of air. It is reasonable to assume that the contaminant transport depends on the flow field but does not affect the flow field because the density of the air does not change with the contaminant concentration. Hence, Eq. (6) can be discretized numerically as Eq. (7).

$$AC=S$$ (7)

where C is the concentration vector, S is the source vector and A is the coefficient matrix. Because the concentration field is unique, the coefficient matrix A is invertible and the inverse matrix B can be obtained by numerical methods such as Gaussian elimination method. Therefore, Eq. (8) is obtained as follows,

$$C=BS$$ (8)

It can also be written as Eq. (9),

$$c_i=b_{i,1}{s}_1+b_{i,2}{s}_2+\mathrm{.......}+b_{i,j}{s}_j+\mathrm{.....}{b}_{i,N}{s}_N=\sum _{j=1}^N{b}_{i,j}{s}_j$$ (9)

Eq. (9) indicates that the element b_ij quantifies the impact of the source at the grid j on the contaminant concentration at the grid i. Therefore, b_ij was named the Spatial Flow Impact Factor (SFIF) by Zhang et al. (2006). This is a brief introduction of SFIF; for a detailed derivation, please see Zhang et al. (2006) and Wang et al. (2013).

The Spatial Flow Impact Factor (SFIF) provides a novel understanding and translation perspective of a flow field. It can easily describe other physical indices reflecting the characteristics of an inhomogeneous flow field, such as air age, accessibility of supply air and accessibility of a contaminant source (ACS) through simple transformation. Therefore, the SFIF can be regarded as an evaluation index for indoor air safety (Zhang et al., 2006). All information about flow field structure, including the relationship between different positions in an air flow field, can be seen from the SFIF matrix. The matrix elements order can be named according to their location number.

2.2.2. The model of integrating the SFIF method Wells–Riley model

On the basis of the classical Wells-Riley model and the concept of SFIF, we propose an improved approach by combining Wells-Riley model and SFIF as follows:

$$P_y=\frac{C}{S}=1-\exp \left(-\sum _{x=1}^{n}SFIF\left(x,y\right)•I\left(x\right)•\theta \left(x\right)•q•t\right)$$ (10)

where x and y are the serial number of discrete units, n is the total number of discrete units, P_y is the PI at cell y, SFIF(x,y) represents the impact of the source at cell x on the contaminant concentration at the cell y, I(x) is the number of infectors at cell x and can be regarded as a distribution function of infectors, with the unit of 1, θ(x) is a correction parameter defined by us, q and t are the quanta generation rates (quanta/h) and exposure time (h), respectively.

Given the influence in the vertical direction, the correction parameter θ(x) was introduced into the formula. Here, θ(x) is defined as:

$$\theta \left(x\right)=\frac{p/Q}{SFIF\left(x\right)}$$ (11)

where p and Q are in the same as in Eq. (1), $\overline{SFIF\left(x\right)}$is the average of all the numbers in the array SFIF(x). SFIF(x) is a collection of SFIF(x,y) where y varies from 1 to n.

Using Eq. (10), the distribution of PI considering the location of infectors and susceptible can be obtained. If we take the effect of air purifiers into consideration (only under the condition that the influence of air purifiers on indoor air flow field can be neglected), Eq. (10) can be extended as:

$$P_y=\frac{C}{S}=1-\exp \left(-\sum _{x=1}^{n}SFIF\left(x,y\right)I\left(x\right)\theta \left(x\right)\left(1-R\left(x\right)\right)\left(1-R\left(y\right)\right)qt\right)$$ (12)

where R(x) and R(y) are the distribution function of the air purifiers’ purification efficiency, expressed as a percent, %.

In general, our new approach requires the following solution procedures: (1) Obtain the convergent flow field of a specific confined space through CFD, then select a reference plane in the space and discretize it into numbered small cells within which well mixed air is assumed. (2) Calculate the matrix of spatial flow impact factors (SFIF), namely, quantitative results of the impact of pollution sources on various points in space. (3) Determine the necessary parameters such as q andθ from the given information. (4) Then determine the spatial distribution of PI using Eq. (10).

Our new model is based on the flow field calculated by CFD, but it is not the same as the CFD-integrated method. When both infected and exposed people’s location changes, the CFD-integrated method requires recalculation, which requires much computing effort (Chen, Lin, Long, & Chen, 2014). Moreover, it is difficult for the CFD-integrated method to determine the optimal location for both susceptibles and infectors based on a one-time calculation of the flow field. That is, the results of the CFD-integrated method cannot provide guidance for optimization of the location of people or facilities to minimize the overall infection risk or the specific infection risk for a given location.

Contrary to that, in our new approach, the results can be obtained even if the both infected and exposed people’s locations are variable. Therefore, it can optimize the location distribution of all people (infected and exposed) and facilities in given restrained conditions.

3. Validation of the new approach

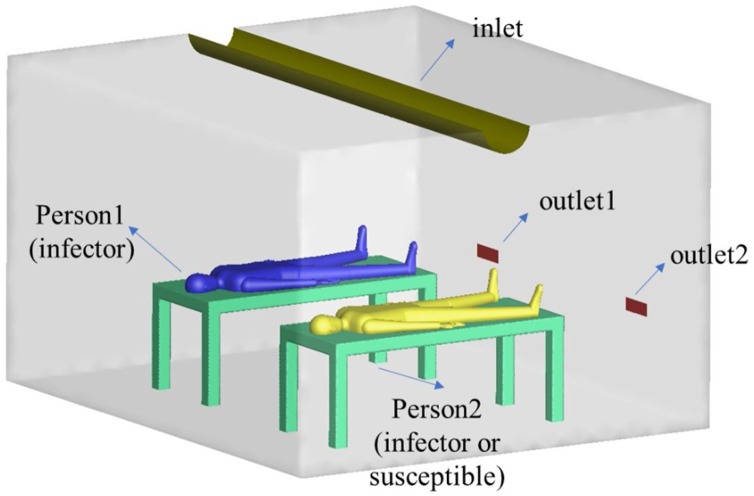
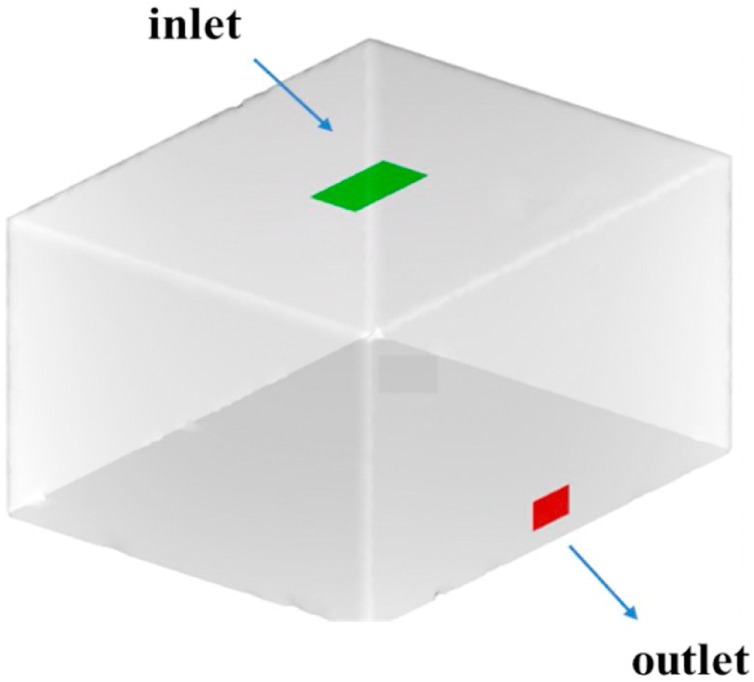
The practicality of the proposed method was verified in a 4.2 m (L) $\times$3.6 m (W) $\times$ 2.5 m (H) simulated hospital ward, which we considered appropriate to test pollutant transmission between two patients (Qian, Li, Nielsen, & Hyldgaard, 2008). Two beds with dimensions of 2 m (L) $\times$0.8 m (W) $\times$0.8 m (H) were placed in the center of the ward and the distance between them was set at 1 m. Two life-sized manikins were placed on the bed to simulate a source patient and a receiving patient. A supply air inlet of a semi-cylinder shape (0.315 m in diameter $\times$4.2 m in length) was installed in the ceiling, two low-level exhaust outlets were set in the wall facing people (Fig. 1 ). The ward is similar to that used by Qian et al. (2008) for their research. The pulmonary ventilation rate for the two manikins was set at 0.36 m³/h and the total supply airflow rate was 151.2 m³/h, which corresponds to 4 air changes per hour (ACH). For illustration purposes, the input parameters are listed in Table 1 .

Fig. 1.

Geometry model of the test ward.

Table 1.

Values of input parameters for validation.

Input parameters of new model	Value
Infectors (I)	1
Susceptible (O)	1
Pulmonary ventilation rate (p)	0.36 m3/h
Quantum generation rate (q)	100 quanta/h
Exposure duration (t)	1 h

We first calculated the uniform probability of infection PI by the classic Wells-Riley model based on the well mixed assumption for comparison. In this case, there is only one infector, so I = 1. According to the given information, p =  0.36 m³/h, Q = 151.2 m³/h. Influenza caused by influenza virus A was chosen for risk estimation, the corresponding quantum generation rate was set at 100 quanta/h (q = 100 quanta/h). This may not correctly approximate an actual case, but is acceptable for our purpose of verifying the feasibility of this study’s method. Assuming the exposure duration is 1 h, the uniform infection risk PI₀ = 21.2 %.

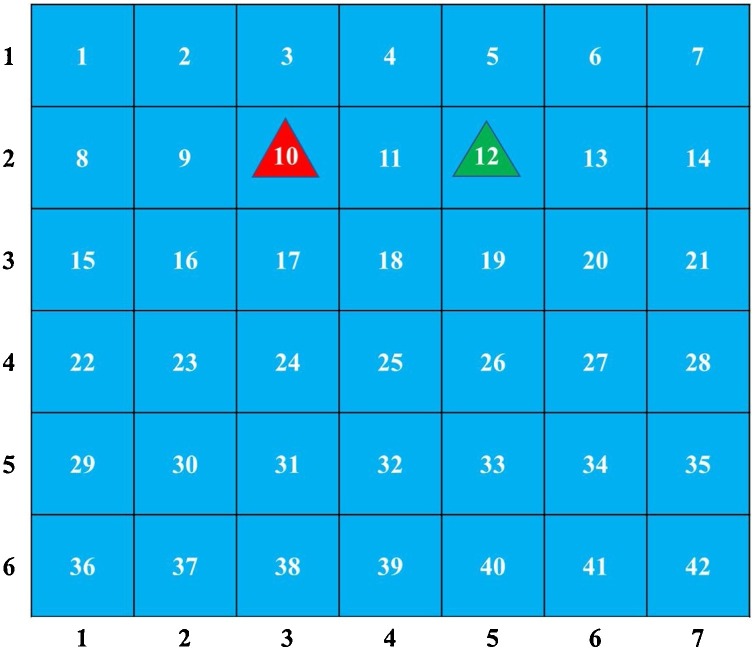
In order to facilitate comparison, one reference plane at the height of the patient's breathing area (1.15 m) was created. Meanwhile, we discretized the plane into 42 ( = 6 × 7) cells and number them. Each cell has a side length of 0.6 m, with the infector located in cell 10 and the susceptible located in cell 12, as shown in Fig. 2 . To get the spatial distribution of infection risk in the ward, both an Eulerian-based approach and our new method were used.

Fig. 2.

Reference plane. The red triangle represents the infector, while the green triangle represents the susceptible.

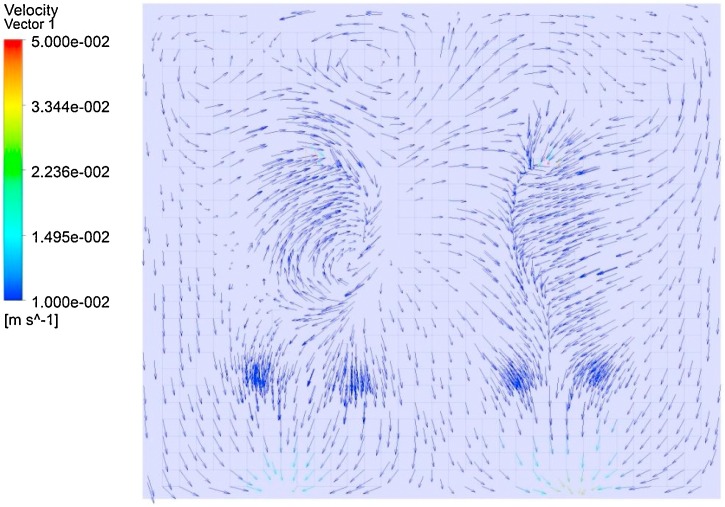
The calculated steady flow field of the ward, and the airflow pattern is shown in Fig. 3 .

Fig. 3.

Airflow structure at the reference plane.

Using calculation of the flow field, the contaminant transport and distribution were calculated. The concentrations for each cell in the reference plane were obtained by averaging the concentrations in their region. The spatial distribution of infection risk can be determined afterwards by substituting the value of concentration in Eq. (5).

Using information for the flow field, the SFIF matrix can be determined. The spatial distribution of PI was obtained by applying Eq. (10).

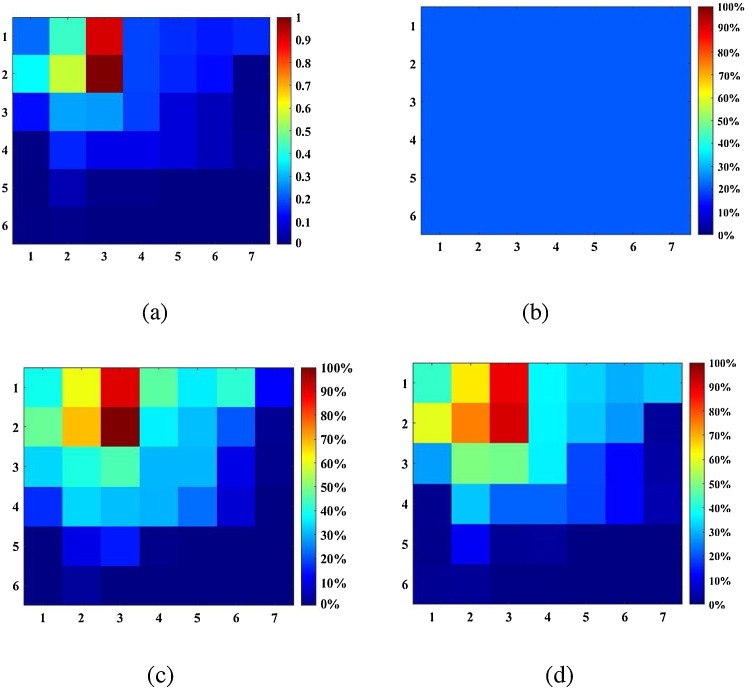
Fig. 4 shows results from the three approaches. The infection risk distribution calculated by the CFD-integrated method and SFIF-integrated method are similar. In addition, we exchanged the location of infector and susceptible and compared results of the three approaches. Our results are consistent with the classic Wells-Riley and with the CFD-integrated results, which validates our method. The differences among the results are because: (1) The number of discrete cells in the SFIF case is limited; the accuracy will increase with the number of cells. (2) The SFIF matrix is three-dimensional, but is treated as two-dimensional for the sake of simplicity.

Fig. 4.

Distribution of (a) SFIF at cell 10 and the probability of infection (PI) calculated by (b) the classical Wells-Riley method, (c) the CFD-integrated method, and (d) the SFIF-integrated method.

4. Applications for controlling cross infection

In addition to obtaining the spatial distribution of PI in confined space, our approach can also be employed to optimize the distribution of people and/or facilities to minimize the probability of cross infection in a given ventilation pattern, that is, provide guidance for controlling infection risk.

4.1. Optimization method

In order to obtain the ideal excessive volumetric specific heat for a building’s internal thermal mass, Zeng, Wang, Di, Jiang, and Zhang (2011) put forward the N-segment method. The authors evenly divide the optimized temperature range into N temperature segments and distribute the excessive volumetric specific heat in the N temperature segments. Then they adjust the values of volumetric specific heat in different temperature segments to minimize the thermal degree of discomfort I, using a non-linear constrained optimization method such as the Sequential Quadratic Programming method (SQP) until the I value reaches a minimum.

From Eqs. (10) and (12), we can adopt the N-segment method to optimally minimize PI in different situations. Using optimization of people’s locations as examples, we define a function O(x), the number of susceptibles at cell x, similar to the definition of I(x). The optimization target is the ideal function of I(x) and O(x) under the following limiting conditions:

$$\begin{array}{ll}a.\sum _{x=1}^{n}I\left(x\right)=M_1\hfill & a.\sum _{x=1}^{n}O\left(x\right)=M_2\hfill \\ c.I\left(x\right)\in \left[0,1,2\dots m_1\right]\hfill & d.\text{O}\left(x\right)\in \left[0,1,2\dots m_2\right]\hfill \end{array}$$

where M₁ and M₂ are the total number of infectors and susceptibles, respectively. m₁ and m₂ are the maximum numbers of infectors and susceptibles in a discrete cell, respectively.

4.2. Optimization background

From the perspective of assuring that the method is universally applicable, we investigated a typical idealized confined space. As illustrated in Fig. 5 , we assume that the infectors and susceptibles are in a 5 m (L) ×4 m (W) ×3 m (H) simulated room with one air supply inlet and air outlet, whose supply airflow rate is 540 m³/h, corresponding to 9 air changes per hour (ACH). The pulmonary ventilation rate for the infectors and susceptibles was set at 0.36 m³/h, the corresponding quantum generation rate was set as 100 quanta/h (q = 100 quanta/h) and the exposure time was 2 h.

Fig. 5.

Model of the confined space.

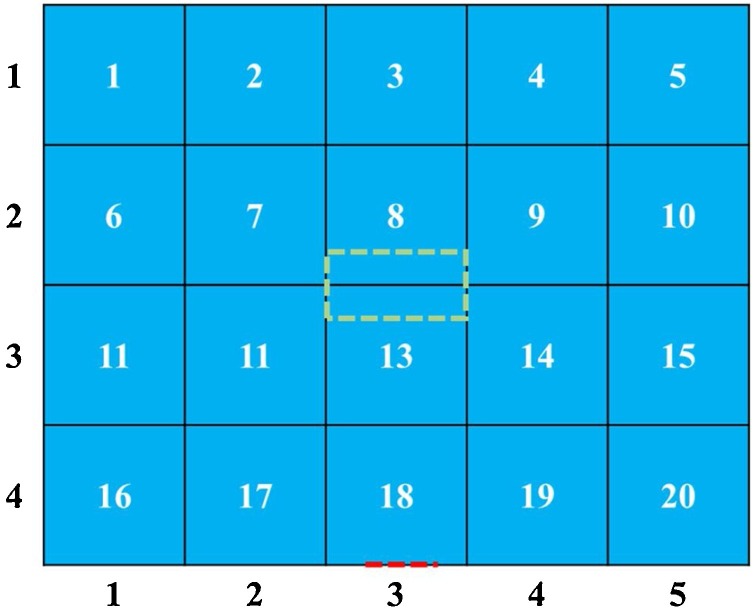
At a height of 1.7 m, a reference plane was discretized into 20 ( = 4 × 5) cells and numbered, each with a length of 1 m, as shown in Fig. 6 .

Fig. 6.

Reference plane at height of 1.7 m. The green and red dashed lines indicate a cast shadow of inlet and outlet onto the reference surface respectively.

To simplify, we categorized the situations into five scenarios, corresponding to each problem (Table 2 ).

Table 2.

Different scenarios.

Scenario	Infector	Susceptible	Purpose
1	Fixed	Fixed	To access PI
2	Fixed	Need optimization	To minimize PI
3	Need optimization	Fixed	To minimize PI
4	Need optimization	Unfixed	To minimize PI
5	Need optimization	Need optimization	To minimize PI

4.3. Results

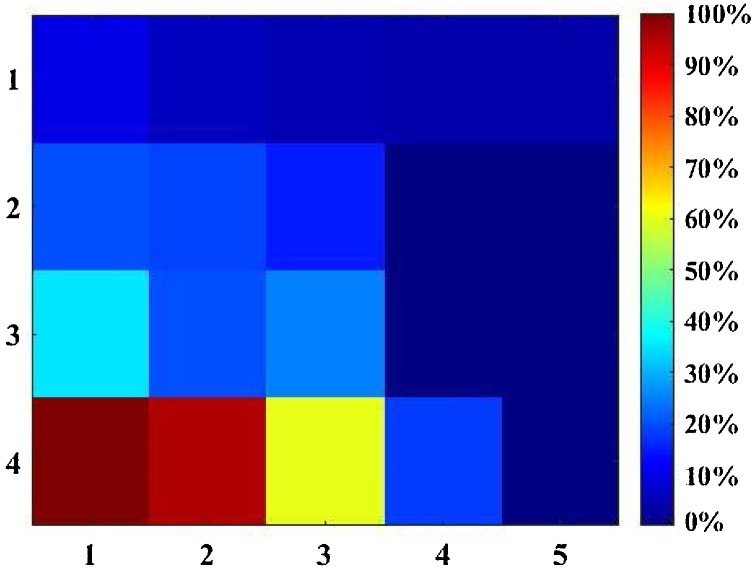
For scenarios 1&2, the locations of infectors were fixed at cell (1,4) and the distribution of PI was obtained from our modified form of the Wells-Riley model, as shown in Fig. 7 . According to the results for PI distribution, for scenario 2 cells (4,2), (5,2), (4,3), (5,3) have the lowest risk of infection.

Fig. 7.

The distribution of possibility of infection (PI).

For scenario 3, the locations of susceptibles were fixed while those of infectors were allowed to vary. That is, for a given O(x), we need to find the optimal I(x) to minimize the risk of cross-infection.

We assume that there are 2 infectors and 1 susceptible in the room, and the susceptible is in cell (5,2). Each cell can hold 1 person at most. In mathematical language, O(10) = 1, O(x, x≠10) = 0. Through inverse problem optimization, we determined the optimal I(x): I(11) = 1, I(16) = 1, I((x, x≠11, x≠16) = 0.

If the susceptible can move around in the space, then the optimization target is to minimize the total PI in the space. The optimal I(x) for scenario 4 is I(5) = 1, I(6) = 1, I((x, x≠5, x≠6) = 0.

For scenario 5, neither the locations of infectors or susceptible were determined, and the optimization result is O(2) = 1, O(x, x≠2) = 0; I(19) = 1, I(20) = 1, I((x, x≠19, x≠20) = 0. Values of input parameters are summarized in Table 3 .

Table 3.

Values of input parameters for optimization.

Input parameters of new model	Value
Infectors (I)	2
Susceptible (O)	1
Maximum number of infectors in per cell	1
Maximum number of susceptible in per cell	1
Pulmonary ventilation rate (p)	0.36 m3/h
Quantum generation rate (q)	100 quanta/h
Exposure duration (t)	2 h

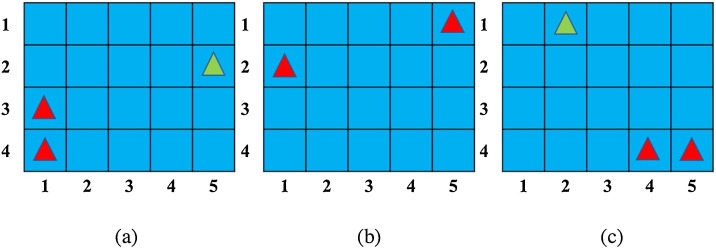
Fig. 8, Fig. 9 show the optimization results. If the infectors are in (1,3) and (1,4), the PI for the susceptible is minimum at (5,2). The PI for the whole space is minimum for the two infectors in (5,1) and (1,2). To obtain a minimum PI for susceptible in the space, the susceptible should locate in (2,1) and the infectors should locate in (4,4) and (5,4).

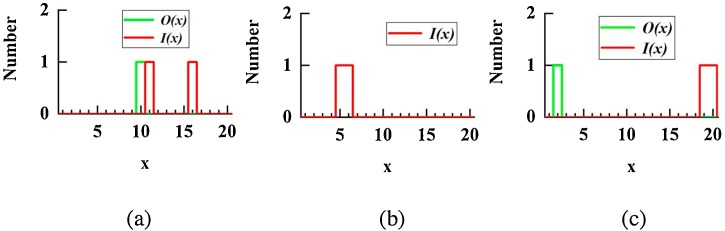
Fig. 8.

(a) Functional image of I(x) and/or O(x) for (a) scenario 3 (b) scenario 4 (c) scenario 5.

Fig. 9.

(a) Location in the reference plane of I(x) and/or O(x) for (a) scenario 3, (b) scenario 4, and (c) scenario 5. Red triangles represnet infectors, green triangles represent susceptibles.

This analysis demonstrates that our method can be applied to estimate PI and optimize people’s locations for various situations. Our new approach can partially compensate for the defects of Wells-Riley model’s well mixed hypothesis. In addition, our new approach can play an important role in controlling infection risk, which is beyond the ability of the CFD-integrated method. For more complicated cases, such as accounting for the distribution of air purifiers and the difference between infectors and susceptibles, it is possible to combine Eq. (12) with the N-segment method and then determine the optimal distribution. The steps are the same as optimizing people’s location in this study.

5. Discussion

COVID-19 is a global challenge, requiring cross-disciplinary cooperation and research to control, in order to maintain the sustainable development of society. Computational biology, big data and artificial intelligence are being used in daily monitoring, prevention and treatment of infectious diseases (Ahmed, Ahmad, Rodrigues, Jeon, & Din, 2020; Bhattacharya et al., 2020; Loey, Manogaran, Taha, & Khalifa, 2020; Zhou, Qiu, Pu, Huang, & Ge, 2020). Abboah-Offei et al. (2021) investigated the impact face mask has had in controlling transmission of respiratory viral infections. Dai and Zhao (2020) estimated the association between infection probability and ventilation rates in confined spaces. Jiang et al. (2020) investigated the effect of comprehensive monitoring of hospital environmental hygiene on the refinement of hospital infection control from a clinical point of view. Leng, Wang, and Liu (2020) developed a numerical strategy to optimize the physical environment in a courtyard, considering the severe impact of COVID-19. Hu, Roberts, Azevedo, and Milner (2020) investigated the multifaceted interrelationships between the built and social environments and assessed their influence on population-level health during the COVID-19 epidemic.

From the perspective of engineering controlling, understanding the distribution of infection probability can help to develop prevention strategies against pandemics. In a space where infectious diseases are airborne transmitted, the probability of infection can vary greatly as a function of the occupants’ location and the airflow pattern. The classic Wells-Riley model and Sun-Zhai model fail to obtain the spatial distribution of the probability of infection (PI). The CFD-integrated method can be applied to overcome the Wells-Riley shortcomings but requires a heavy computing load.

In our validation case, the CFD-integrated method required a computational grid of 4 × 10⁶ control volumes, which in turn required 10 CPU cores on a high-performance computer and about 20 h to achieve reliable results. If the location of the infector changes, recalculation is necessary, and the calculation time will multiply. Therefore, the calculation was difficult to conduct on an ordinary office computer with insufficient memory and CPU power. Similar studies have shown that for an accurate simulation of a kitchen room, CFD would require at least 10⁶ control volumes (Chen et al. (2020). Chen et al. (2018) used a grid of 4 × 10⁶ control volumes for an accurate simulation of an office room with a ceiling fan. Hence, high computing cost prevents CFD from becoming the primary tool for indoor environmental simulations (Morozova, Trias, Capdevila, Pérez-Segarra, & Oliva, 2020).

In comparison with the CFD-integrated method, our SFIF-integrated method is simple to operate with lower consumption of computing resources while the accuracy of the calculation is within an acceptable range. On the basis of the flow field calculated by the CFD method, our computing time can be limited to 5 min on an ordinary office computer. Our advantage in computation costs is even more pronounced when an infector's position changes.

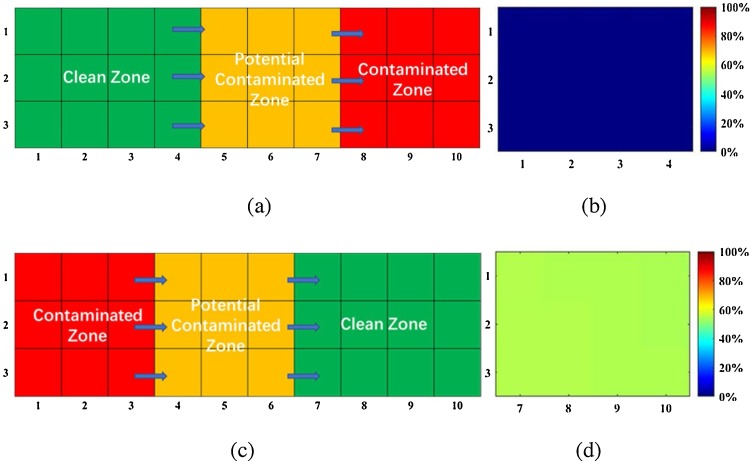
From the perspective of controlling infection, Dai and Zhao (2020) suggest that increasing the volume of fresh air can control the infection risk to within a safe level, but accept the well mixed assumption and do not take the location distribution into account. We investigated the PI in a simplified Fever Clinic with different distributions of the Clean Zone, Potentially Contaminated Zone and Contaminated Zone. Fig. 10 shows that for the same amount of fresh air, the infection risk varies greatly according to location of the occupants. Even if the PI calculated by Wells-Riley model is within safe limits for a given ACH, the actual PI can be beyond the safe range for some positional arrangements. The details of our calculation are attached in the Appendix A. In controlling the risk of cross infection, effects of the flow field and the distribution of people’s locations are non-negligible factors.

Fig. 10.

(a) Optimal distribution of three zones (b) PI distribution of Clean Zone for the optimal distribution (c) a poor distribution of the three zones (d) the PI distribution of Clean Zone for the poor distribution.

Therefore, a model that can provide guidance for both infection risk assessment and location arrangement to minimize PI is of great value. As flow field information can be stored in the SFIF matrix and then converted to a function describing position, our SFIF-integrated model can be combined with the N-segment method and used to obtain the optimal arrangement of people and facilities (e.g. air purifiers), so as to minimize the cross-infection risk, whereas the CFD-integrated method cannot do this.

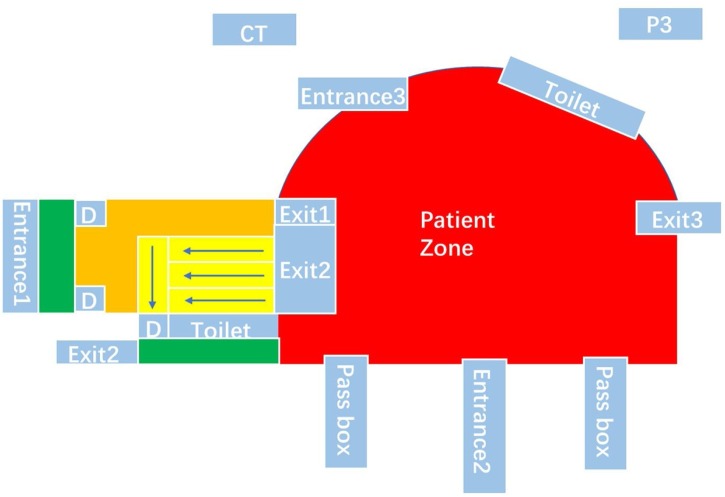
As our new approach can investigate problems from a macro perspective, and does not rely on detailed information, it is useful in controlling the spread of infection in various scenarios. For example, it is particularly suitable for use in the Fangcang shelter hospitals (Fig. 11 ), designed and built in mainland China and which most recently proved invaluable for caring for COVID-19 patients.

Fig. 11.

the layout of Wuhan Jianghan Fangcang shelter hospital in Hubei Province, China. Exit1 – Cleaning and police officers exit; Exit2 – Medical personnel exit; Exit3 – Sewage exit; Entrance1 – Cleaning and police officers entrance and exit; Entrance2 –Medical personnel entrance and exit; Entrance3 – Patients entrance; D – door.

As the Fangcang shelter hospitals are reconstructed on the basis of the existing stadium or factory workshops, they may not satisfy the requirements of design for controlling infectious disease. Through our method, we can verify whether the original layouts are adequate for satisfying the requirements and determine the optimal layouts to replace the original one if necessary.

Moreover, increasing the number of patients admitted to a hospital increases the hospital’s PI. During a pandemic, the number of inpatients in hospitals increases sharply, and sometimes hospitals are overwhelmed. Therefore, it is very important to maximize the use of hospital space and equipment, control the risk of infection, and manage the occupancy rate of hospitals simultaneously. Through our approach, it is reasonable to determine the optimal distribution of different zones, in areas such as patient rooms, staff areas, toilets and activity space. By minimizing PI, we can make the best use of the space and equipment of a hospital, provide protection for healthcare workers, improve the living conditions for patients and promote their recovery. Optimization of factors such as ventilation, ventilation sources and distribution that affect PI requires considering several factors simultaneously. We hope that our new approach can contribute to such a project, such that hospital space can be used more efficiently, and patient capacity can be safely increased.

There are several limitations of our study. First, the modified model was developed in the case of airborne transmission of infectious disease, while droplet transmission and direct contact has been confirmed as significant path to spread virus. Second, we have ignored the influence of human respiratory activity and human thermal plumes on the flow field has been ignored. Consequently, our method may not be suitable for situations in which there is crowding in a narrow space. Third, for simplicity, we have transformed a three-dimensional problem into a two-dimensional problem by creating a plane at the height of the person's breath area and investigating this plane. This approach is common; for example, Wang et al. (2013) employed an SFIF modified method to identify the point source of indoor gaseous contaminant and selected a two-dimensional case as a demonstration case. This may lead to errors when the objects of interest are not on the same plane. Hence, it is necessary to extend our method to three dimensions. Finally, the present study illustrates the principle and usage of our new approach in a semi-qualitative and semi-quantitative manner, but since the specific application in real scenarios is limited, this will dominate our next phase of research.

6. Conclusion

This paper presents a new approach to assessing and controlling infection risk: integrating the spatial flow impact factor (SFIF) method with the Wells-Riley model. As the classical Wells-Riley model fails to obtain the spatial distribution of PI, it is sometimes difficult to formulate effective measures to prevent infection diseases. Our approach can be used to determine the spatial distribution of PI based on once calculation of the flow field, even though the location of infectors is not fixed. In addition, when combined with anti-problem approach, it can provide guidance for optimizing the location of persons and facilities in a confined space, extending the application of modified Wells-Riley equation. In this way, we can control the infection risk in a built environment effectively and make the best use of the space and resources to curb the spread of infectious disease. Our method can be developed and employed in real scenarios (e.g. Fangcang shelter hospitals) to help expand the capacity of hospitals and protect healthcare workers and patients, contributing to maintaining the sustainable development of society.

Declaration of Competing Interest

The authors report no declarations of interest.

Appendix A.

According to the current design and management regulations in mainland China, the Fever Clinic (FC) should be divided into three zones: Clean Zone, Potentially Contaminated Zone and Contaminated Zone, and these three zones must be strictly separated from the rest of the hospital (Wang et al., 2020). The ventilation should generate unidirectional airflow which flows from the Clean Zone to the Potential Contaminated Zone and then to the Contaminated Zone.

We want to compare the difference in PI of different distributions in the three zones with the same ventilation condition. As the consulting rooms are usually relatively independent, we mainly focus on the connected areas in the FC. In our research, the connected area of FC is abstracted as a cuboid with displacement ventilation, and dimensions of 30 m (L) ×9 m (W) ×3 m (H). We selected a reference plane at the height of 1.7 m, and discretize it into 42 cells, as shown in Fig. 1.

We assume that the infector densities are 0.5 people per cell and 0.1 people per cell in the Potential Contaminated Zone and Contaminated Zone, respectively. The q is set as 100 quanta/s (Zhang, 2020), the occupants’ pulmonary ventilation p is set at 0.36 m³/h, and the ACH is set as 12.

Assuming that the exposure time is 1 h and the area ratio among the Clean Zone, Potentially Contaminated Zone and Contaminated Zone is 4:3:3, we obtained the optimal and one unreasonable distribution of the three zones, as shown in Fig. 10. The optimal distribution is determined by our new approach and is consistent with the regulations in mainland China. The uniform PI calculated by Wells-Riley model is 1.83 %, while for the optimal distribution, the PIs in the Clean Zone are all under 0.2 %. For the poor distribution, the PIs in the Clean Zone all approach 50 %, a dangerous arrangement.